2. 中国石油大学(北京)石油与天然气工程学院;
3. 北京工业大学
2. College of Petroleum and Natural Gas Engineering, China University of Petroleum(Beijing);
3. Beijing University of Technology
0 引言
固井质量对整个油气生产至关重要,然而注水泥固井时,水泥浆往往不能将环空中的钻井液顶替完全,滞留的钻井液形成窜槽,使得固井质量降低。其次,页岩储层通常采用水平井技术进行开采,但是由于下套管过程中大斜度井段以及水平井段套管所受的重力方向不再是轴向而是径向,极易导致套管偏心,使得固井后套管外壁的水泥环厚度出现差异[1]。如果忽略固井质量来进行套管强度设计,则有可能导致体积压裂过程中套管完整性失效[2-6]。
目前关于固井质量对套管应力的影响分析主要基于传统的建模方法,即一次性直接对井筒组合体施加外部载荷,忽略了井筒组合体的初始应力应变,导致计算过程无法考虑水泥浆失重以及压裂过程中地层性质变化对套管的影响,因此不再适用于页岩气体积压裂过程中的套管力学分析[7-10]。鉴于此,笔者基于分步有限元方法,考虑了井筒组合体的初始应力应变,建立了温度和压力耦合条件下含多重工程缺陷的井筒组合体开挖扰动力学模型,对压裂过程中极端工况下的套管力学行为进行分析,以期为页岩气开发提供理论指导。
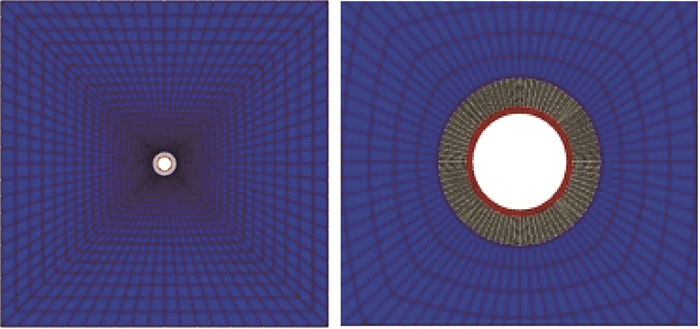
1 数值模型建立 1.1 传统模型套管-水泥环-地层组合体传统有限元模型如图 1所示。模型中套管-水泥环-地层组合体共同承受来自远场地应力与套管内的外部载荷。这种一次性直接对井筒组合体施加外部载荷的方法为传统建模方法,笔者后续所指的传统模型均为基于上述建模方法所构建的模型。
|
| 图 1 套管-水泥环-地层组合体传统有限元模型 Fig.1 Finite element model of casing-cement sheath-formation |
1.2 页岩气井筒组合体力学新模型
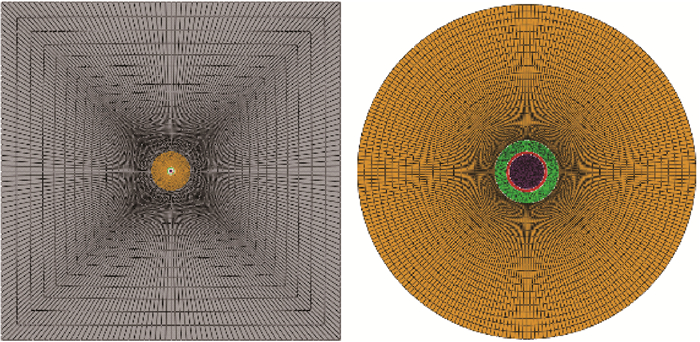
根据岩石力学和弹塑性力学理论,可以将研究的问题简化为平面应变问题。根据前文的基本假设,建立如图 2所示的套管-水泥环-地层有限元模型。套管、水泥环和地层均采用扫掠网格划分。为了保证计算的精度,对模型中的井眼周围进行网格加密。
|
| 图 2 套管-水泥环-地层组合体有限元模型 Fig.2 Finite element model of casing-cement sheath-formation |
为了计算方便,做以下假设:①固井分析步中,水泥浆瞬间变为凝固以后的水泥环,此时水泥环没有剪应力,处于静水应力状态[11]。②当水泥浆失重时,水泥环初始应力为0 MPa[12]。模拟共可以分成4个阶段。
(1) 对未钻井储层施加远场地应力。
(2) 挖除井眼,并在壁面施加钻井液液柱压力,以模拟钻井过程中井周变形与应力状态。
(3) 为便于计算,可同时把水泥环和套管加入模型中,使得水泥环外边界与变形后的井眼形状完全匹配。
(4) 在套管内壁上施加压力载荷以模拟后期作业过程中的井下条件变化。
数值计算过程中,在第1阶段,需要杀死套管和水泥环单元,并利用ABAQUS软件中的预定义场功能先对地层材料加载初始地应力,并使外边界完全约束。第2阶段则需杀死井眼内部岩石单元,并在井眼内壁施加液柱压力。第3、第4阶段则分别激活套管单元和水泥环单元。
以长宁威远区块的W201-h1井为例进行分析。该井采用∅139.7 mm、TP95S射孔套管完井,套管壁厚9.17 mm。地层各参数为:22 MPa的上覆岩层压力,24 MPa的最小水平主应力,38 MPa的最大水平主应力。井筒内静液柱压力20 MPa,压裂时井筒内压力64 MPa。此外,压裂井段储层初始温度65 ℃,施工时注液温度20 ℃,注液时间3 600 s。模型具体几何参数、材料特性以及热力学参数见表 1和表 2。
| 介质 | 外径/mm | 内径/mm | 弹性模量/GPa | 泊松比 | 内摩擦角/(°) | 黏聚力/ MPa |
| 套管 | 139.7 | 121.4 | 210.0 | 0.30 | — | — |
| 水泥环 | 215.9 | 139.7 | 15.0 | 0.15 | 17.1 | 21.6 |
| 地层 | — | — | 36.0 | 0.20 | 30.0 | 59.3 |
| 介质 | 密度/ (kg·m-3) | 膨胀系数/ ℃-1 | 比热容/(J· kg-1· ℃-1) | 导热系数/(W· m-1· ℃-1) |
| 套管 | 7 800 | 1.22e-5 | 460 | 45.0 |
| 水泥环 | 1 800 | 1.05e-5 | 865 | 0.9 |
| 地层 | 2 300 | 1.03e-5 | 896 | 2.2 |
模型建立时忽略了沿井眼轴向方向上的温度传导。
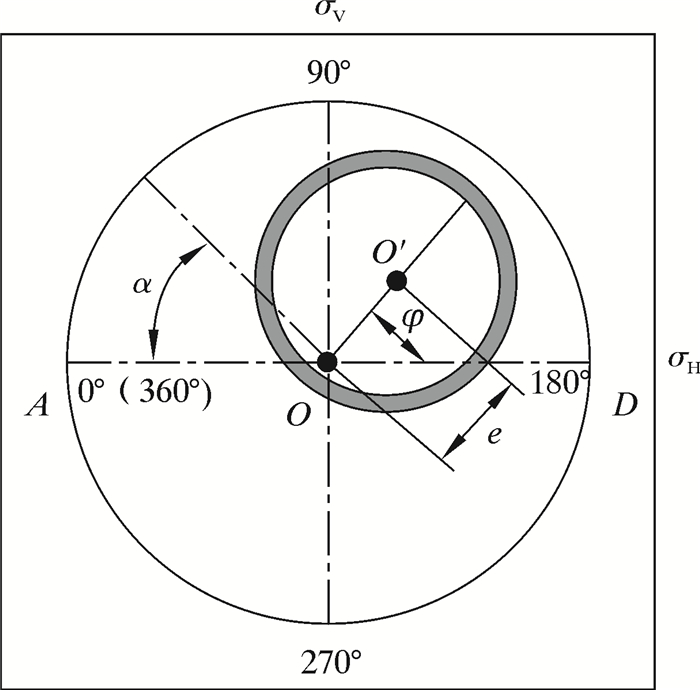
1.2.1 套管偏心建立的套管偏心有限元模型如图 3所示。模型中,井眼中心为点O, 套管中心为点O′,偏心距为e, 偏心角为φ。模型设置套管偏心角为0°,偏心距30 mm。模型力学以及材料参数与上节一致。其中套管内初始静液柱压力20 MPa,注液时井筒内压力64 MPa。
|
| 图 3 套管-水泥环-地层组合体模型 Fig.3 Casing-cement sheath-formation model |
图 4为不同注液温度下,套管偏心对套管应力的影响规律。从图 4可以看到:当套管偏心距为30 mm时,随着高压流体的泵入,套管的应力有所增加,与不考虑温降的情况相比,偏心条件下冷流体的注入导致套管应力有所降低;而当水泥浆发生失重时,套管的应力进一步减小。由此可知,高压注液期间,当套管发生偏心时,偏心对套管的影响是主要因素。
|
| 图 4 不同注液温度下套管偏心对套管应力的影响规律 Fig.4 Effect of casing eccentricity on casing stress under different injection fluid temperature |
1.2.2 水泥环缺失+偏心
前人通过现场与室内试验发现,实际情况下水泥环缺陷形态复杂。鉴于此,笔者分别研究了水泥环周向缺失、套管偏心与水泥环缺失组合作用下的套管应力变化规律。
1.2.2.1 周向缺失模型假设水泥环缺失角度为α,圆周角度沿水平方向顺时针依次为0°~360°。模型中套管居中,则偏心距为0 mm,偏心角为0°,取水泥环缺失角为0°~360°来进行模拟计算。模型材料参数以及相应应力参数设置不变。模拟结束后,在套管内壁顺时针取若干节点,提取对应的参数,绘制相应参数随节点路径变化的曲线。
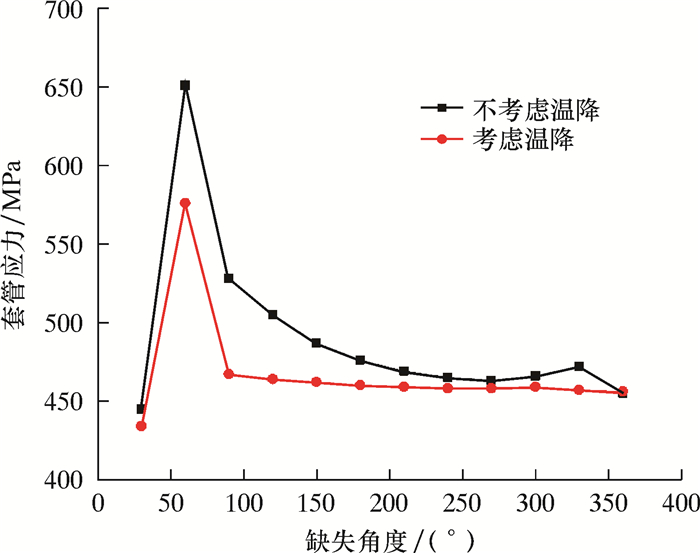
图 5为不同注液温度下,水泥环周向缺失不同角度时套管应力的变化规律。从图 5可见:不同注液温度下,随水泥环缺失角度的改变,套管应力的变化规律基本一致,即当水泥环开始出现缺失时,水泥环缺失处会产生明显的应力集中,套管应力快速增大,在50°左右时达到最大,随后套管应力随着水泥环缺失角度的增大而逐渐减小;在缺失角度为360°时,套管应力降到460 MPa,但是此时套管失去水泥环的保护,很可能在后续的压裂改造以及油井生产过程中发生剪切、挤压等变形损毁。此外,水泥环缺失时,井筒内的传热作用导致套管应力有不同程度的减小。
|
| 图 5 水泥环缺失时,不同注液温度下套管应力变化规律 Fig.5 Change of casing stress under different injection fluid temperatures without cement sheath |
1.2.2.2 套管偏心+水泥环缺失
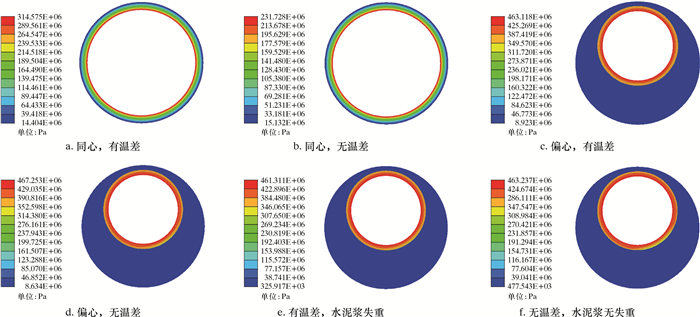
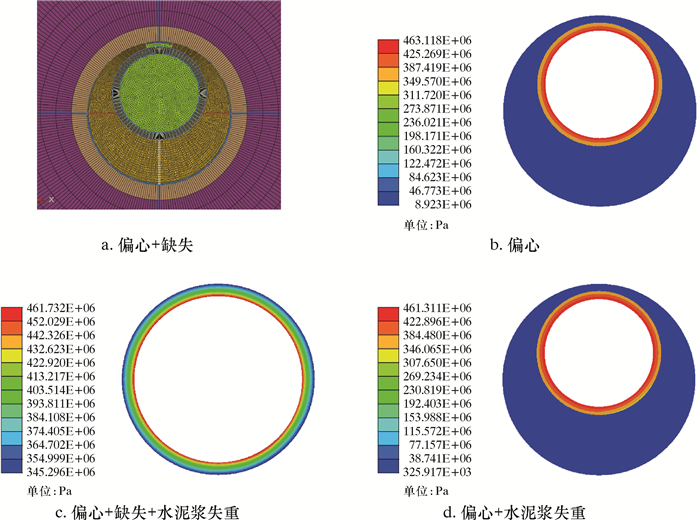
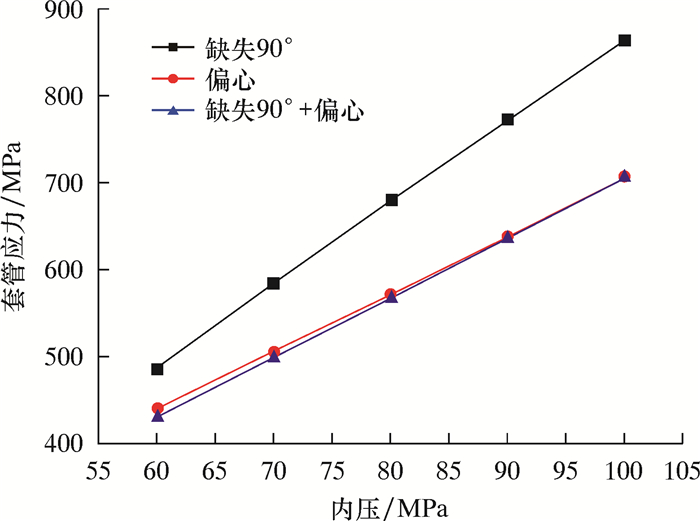
多重工程缺陷存在时套管应力模拟结果如图 6所示。模型中设置套管偏心距为30 mm,偏心角为0°,即水平最大主应力方向,缺失位置如图 6a所示,其他参数设置不变。通过模拟计算可得到套管偏心与水泥环缺失组合作用下套管应力的变化规律。如图 6c所示,当水泥环缺失发生在偏心方向时,套管应力有所降低,同时水泥浆的失重导致套管应力进一步降低。内压对套管应力的影响如图 7所示。从图 7可见,随着井筒内压的增大,水泥环缺失对套管应力的影响最为显著。
|
| 图 6 多重工程缺陷存在时套管应力模拟结果 Fig.6 Simulation results of casing stress in the presence of multiple engineering defects |
|
| 图 7 内压对套管应力的影响(含结构缺陷) Fig.7 Effect of internal pressure on casing stress (including structural defects) |
2 现场案例验证
现场油气井失效案例统计如表 3所示。由表 3可见,与未发生套管失效的压裂段比,失效段地层压裂具有低压力、高排量、大规模的特点,比例达到48%。套管失效显著发生在压裂较困难地层(施工压力相对很高,加砂困难)的比例几乎为0,且失效井段存在水泥环窜槽缺失的问题。
| 井号 | 失效区域/m | 压裂特点(相对于未套损压裂段) |
| W201-h1 | 1 882、2 331 | 低压力、高排量、大规模 |
| N201-h1 | 3 491 | 低压力、高排量、大规模 |
| N201 | 2 441 | 低压力、高排量、大规模 |
| Nh3-1 | 2 930~2 934 | 低压力、高排量、大规模 |
| Q-10 | 3 162~3 171 | 低压力、高排量、大规模 |
以W201-h1井为例,该井在前四级压裂施工过程中便出现了2次套损,第1次套损发生在第1段压裂完成后,连续管在起出过程中遇阻并在2 535 m处拉断。后续钻桥塞过程中,井下工具在2 579 m处再次遇阻,说明此井段套损严重。第2次套损则出现在第3段压裂后的2 331 m处,也是在下桥塞过程中遇阻从而发现套管损坏。两次套损段的套后成像测井图像如图 8所示。在这两段均出现了较为严重的水泥窜槽缺失问题,该井段水泥环空部分被流体充填,极易在压裂时被压窜。统计发现,该井固井质量在多处压裂段以中差为主,部分井段出现较为严重的固井质量问题。

|
| 图 8 套后成像测井图像 Fig.8 Image logging through casing |
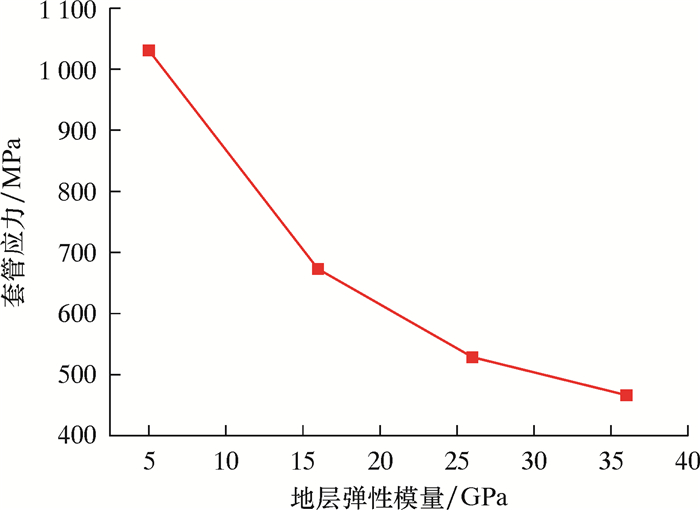
其次,W201-h1井所处的地质特征天然裂缝断层发育,压裂过程中具有低压力、大排量、大规模的特点,说明地层被“打碎”程度高,即地层的综合弹性模量有所下降[13-14]。为此模拟了水泥环缺失90°时,套管应力随地层弹性模量的变化规律(见图 9)。从图 9可见,当地层弹性模量降至10 GPa时,套管应力已经超过其屈服强度而发生破坏,与实际情况相符。
|
| 图 9 地层弹性模量对套管应力的影响(水泥环缺失90°) Fig.9 Effect of formation elastic modulus on casing stress (90° cement sheath missing) |
3 施工参数优化 3.1 套管壁厚
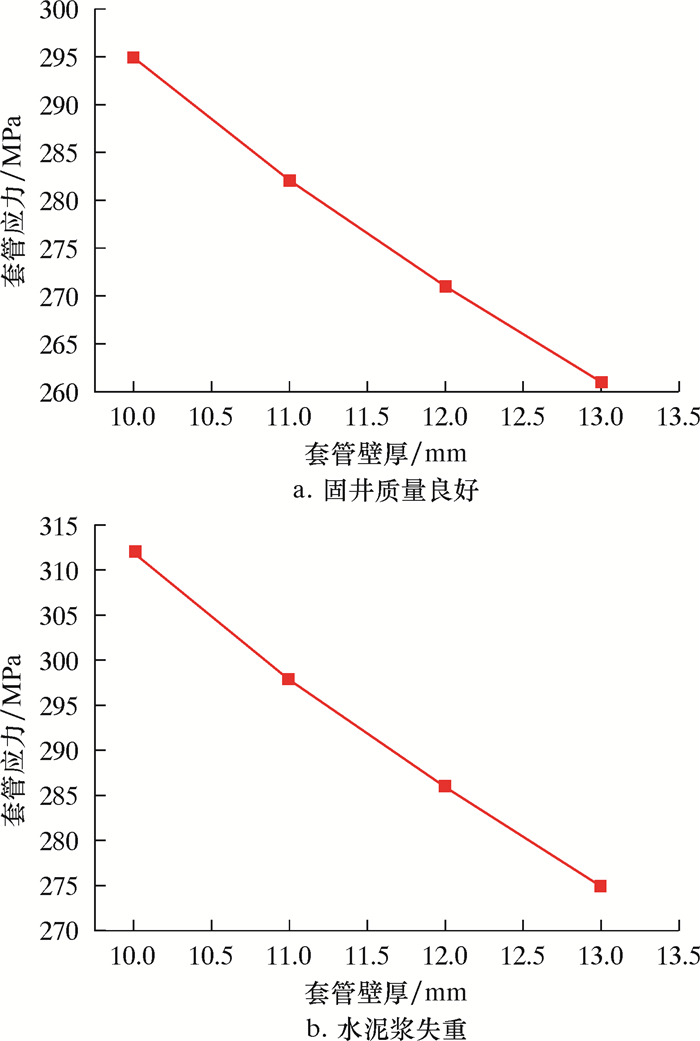
选用适当钢级或者一定壁厚的套管是保证套管完整性较为常用的一种方法。套管的钢级越高,其屈服强度相应就越高。由于中国页岩气区块地质特征较为复杂,考虑到今后页岩气开发过程中会对套管的壁厚有进一步的要求,为此模型设置套管壁厚分别为10、11、12和13 mm,研究套管壁厚对井筒完整性的影响。对于井筒结构完整的情况,模拟结果如图 10所示。
|
| 图 10 套管壁厚对套管应力的影响 Fig.10 Effect of casing wall thickness on casing stress (good cementing quality) |
从图 10可见:随着套管壁厚的增加,套管应力线性降低;当水泥浆发生失重时,套管应力依然小于屈服强度。
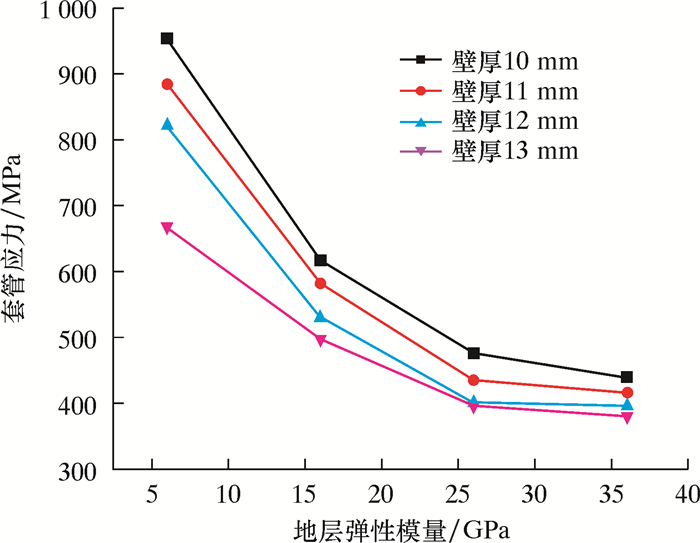
含工程缺陷(缺失+失重)时套管壁厚对其应力的影响如图 11所示。从图 11可见:随着地层弹性模量的降低,水泥环缺失对套管应力的影响逐渐加强,当地层弹性模量降至5 GPa时,套管应力已经超过了其屈服强度;当套管壁厚增加至13 mm时,套管应力逐渐下降并处于安全状态。
|
| 图 11 套管壁厚对其应力的影响(缺失+失重) Fig.11 Effect of casing wall thickness on casing stress (cementing weightlessness) |
3.2 水泥环弹性模量
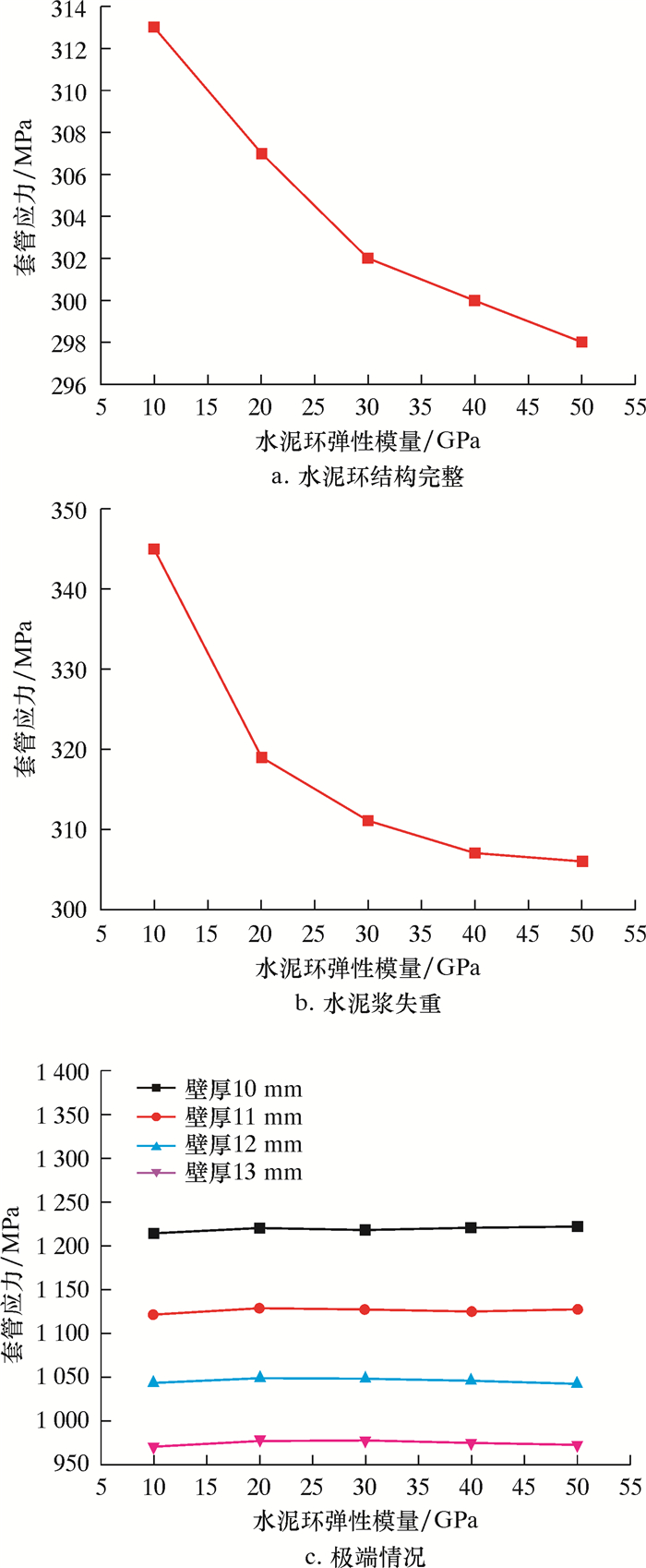
水泥环结构完整及顾及在工程缺陷时水泥环弹性模量对套管应力的影响如图 12所示。从图 12可见,水泥环结构完整时,无论水泥浆是否发生失重,套管应力均随着水泥环弹性模量的增加而减小。这是因为水泥环刚性的增加限制了套管向外侧的扩张。但是水泥浆失重会导致水泥环初始应力降低,从而使得水泥环对套管的束缚作用减小,因此水泥浆失重情况下的套管应力大于水泥浆没有失重的情况(见图 12a)。
|
| 图 12 水泥环弹性模量对套管应力的影响 Fig.12 Effect of elastic modulus of cement sheath on casing stress |
基于以上分析发现,当水泥环结构完整时,无论水泥浆是否发生失重,套管应力始终处于安全状态,水泥环弹性模量的变化并不足以导致套管发生失效变形。
如图 12c所示,极端情况下(压裂过程中地层弹性模量降至6 GPa,内压100 MPa,水泥环缺失90°),水泥环弹性模量的调整并不能有效改善套管的应力状态。
4 结论(1) 套管偏心和水泥环缺失单独作用时对套管应力的影响较大,随着井筒内压的增大,水泥环缺失对套管应力的影响尤为显著。
(2) 当存在工程缺陷时,地层弹性模量的降低对套管应力的影响加剧,套管应力迅速增大并超过其屈服强度。通过降低水泥环弹性模量来改善套管受力状态的作用较小,采取增加套管壁厚的方法有助于避免其发生损毁失效。
| [1] | AKGUN F, AL-GHADBAN H. Simulation investigation of casing eccentricity estimation for different inclination angles and tensile forces using finite element method[R]. SPE 91811-MS, 2004. |
| [2] |
薛承瑾. 页岩气压裂技术现状及发展建议[J].
石油钻探技术, 2011, 39(3): 24-29.
XUE C J. Technical advance and development proposals of shale gas fracturing[J]. Petroleum Drilling Techniques, 2011, 39(3): 24-29. DOI: 10.3969/j.issn.1001-0890.2011.03.004 |
| [3] |
戴强. 页岩气井完井改造期间生产套管损坏原因初探[J].
钻采工艺, 2015, 38(3): 22-25.
DAI Q. Preliminary study on the causes of production casing damage during shale gas well completion reconstruction[J]. Drilling and Production Technology, 2015, 38(3): 22-25. |
| [4] |
郭雪利, 李军, 柳贡慧, 等. 温-压作用下水泥环缺陷对套管应力的影响[J].
石油机械, 2018, 46(4): 112-118.
GUO X L, LI J, LIU G H, et al. Influence of cement sheath defect on casing stress under temperature-pressure effect[J]. China Petroleum Machinery, 2018, 46(4): 112-118. |
| [5] |
田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J].
天然气工业, 2015, 35(9): 70-76.
TIAN Z L, SHI L, QIAO L. Problems and countermeasures of shale gas horizontal wellbore integrity[J]. Natural Gas Industry, 2015, 35(9): 70-76. DOI: 10.3787/j.issn.1000-0976.2015.09.010 |
| [6] |
高利军, 柳占立, 乔磊, 等. 页岩气水力压裂中套损机理及其数值模拟研究[J].
石油机械, 2017, 45(1): 75-80.
GAO L J, LIU Z L, QIAO L, et al. Mechanism analysis and numerical simulation of casing failure in hydraulic fracturing of shale gas formation[J]. China Petroleum Machinery, 2017, 45(1): 75-80. |
| [7] |
蒋可, 李黔, 陈远林, 等. 页岩气水平井固井质量对套管损坏的影响[J].
天然气工业, 2015, 35(12): 77-82.
JIANG K, LI Q, CHEN Y L, et al. Influence of cementing quality of shale gas horizontal well on casing damage[J]. Natural Gas Industry, 2015, 35(12): 77-82. DOI: 10.3787/j.issn.1000-0976.2015.12.012 |
| [8] |
范明涛, 柳贡慧, 李军, 等. 页岩气井温压耦合下固井质量对套管应力的影响[J].
石油机械, 2016, 44(8): 1-5.
FAN M T, LIU G H, LI J, et al. Effect of cementing quality on casing stress under shale gas well temperature and pressure coupling[J]. China Petroleum Machinery, 2016, 44(8): 1-5. |
| [9] |
刘奎, 高德利, 王宴滨, 等. 局部载荷对页岩气井套管变形的影响[J].
天然气工业, 2016, 36(11): 76-82.
LIU K, GAO D L, WANG Y B, et al. Effect of local load on casing deformation of shale gas well[J]. Natural Gas Industry, 2016, 36(11): 76-82. DOI: 10.3787/j.issn.1000-0976.2016.11.010 |
| [10] |
于浩, 练章华, 林铁军. 油田固井质量对套管损坏影响的数值仿真[J].
计算机仿真, 2014, 31(9): 161-164.
YU H, LIAN Z H, LIN T J. Numerical simulation of influence of oilfield cementing quality on casing damage[J]. Computer Simulation, 2014, 31(9): 161-164. DOI: 10.3969/j.issn.1006-9348.2014.09.035 |
| [11] |
范明涛, 李军, 柳贡慧. 页岩地层体积压裂过程中水泥环完整性研究[J].
石油机械, 2017, 45(8): 45-49.
FAN M T, LI J, LIU G H. Study on cement sheath integrity in shale formation fracturing process[J]. China Petroleum Machinery, 2017, 45(8): 45-49. |
| [12] |
沈吉云, 石林, 李勇, 等. 大压差条件下水泥环密封完整性分析及展望[J].
天然气工业, 2017, 37(4): 98-108.
SHEN J Y, SHI L, LI Y, et al. Analysis and perspective of cement sheath integrity under a high differential pressure[J]. Natural Gas Industry, 2017, 37(4): 98-108. |
| [13] | LIAN Z H, YU H, LIN T J, et al. A study on casing deformation failure during multi-stage hydraulic fracturing for the stimulated reservoir volume of horizontal shale wells[J]. Journal of Natural Gas Science and Engineering, 2015, 23: 538-546. DOI: 10.1016/j.jngse.2015.02.028 |
| [14] |
田锋. 裂缝体的弹性模量和裂缝密度[J].
地质学报, 2007, 81(10): 1338-1344.
TIAN F. Elasticity modulus and fracture density in the rocks with crevices[J]. Acat Geologica Sinica, 2007, 81(10): 1338-1344. DOI: 10.3321/j.issn:0001-5717.2007.10.004 |



