2. 中石化中原储气库有限责任公司;
3. 中国石油技术开发公司
2. Sinopec Zhongyuan Gas Storage Co., Ltd.;
3. China Petroleum Technology Development Company
0 引言
储气库注采管柱不同于一般的采气井管柱,注采气周期性频繁交替,气体在管柱和地层之间双向流动,注采气压力在13~42 MPa之间变化;同时,地温梯度每100 m高达3.4 ℃,这些复杂交变载荷的作用,对管柱的连接强度和密封性产生了较大影响,极易造成管柱疲劳损坏[1]。管柱接头的密封部位是决定承受交变载荷的关键结构,深入研究其接触压力的变化规律,对于合理选用密封结构形式和提高注采管柱密封承载能力具有重要意义。储气库管柱特殊螺纹接头的密封功能不依赖于螺纹配合,主要依靠金属/金属径向密封结构来实现,常见的结构形式有锥面/锥面、弧面/锥面和球面/柱面等,接头的扭矩台肩也可实现辅助密封。
黄翠英等[2]建立了特殊螺纹接头的有限元模型,模拟储气库运行工况,分析了套管接头的Von Mises等效应力和接触压力分布,对接头密封面、台肩面及螺纹面的密封性能进行了评价。祝效华等[3]研究了拉弯复合载荷作用下套管连接螺纹的应力分布规律,讨论了井眼曲率(弯矩)对套管连接强度和密封性能的影响。王建东等[4]对比了锥面/锥面和弧面/锥面两种密封结构在多种载荷条件下接触压力和接触长度变化情况,窦益华等[5]模拟交变拉伸载荷和交变压缩载荷,分析了锥面/锥面、球面/柱面两种接头密封面的接触压力变化,结果表明,随交变拉伸载荷周期的延长,两种接头密封面最大接触压力均呈现减小趋势。王建军[1]进行了注采管柱全尺寸气密封循环试验,表明注采管柱经压缩载荷后,再拉伸时易发生泄漏。拉压交变载荷下注采管柱耐压缩密封能力较低,多周次交变循环后,额定密封承载能力有所下降。K.HAMILTON等[6]采用超声技术测试螺纹接头密封表面之间的接触应力,用以准确评价油套管柱特殊螺纹接头的密封能力。J.R.XIE等[7]考虑接头几何结构、材料参数以及运行工况的不确定性和变动性,提出了一套基于可靠度的设计、定量评价方法,以此来分析高温、高压井油套管柱接头的密封性能。
笔者基于弹塑性接触非线性理论,采用有限元分析方法,重点考察拉压交变载荷作用下,注采管柱接头密封结构接触压力的分布特点。通过研究两种密封结构(球面/柱面、锥面/锥面)的接触压力变化情况,探讨交变载荷下接触压力随接触长度的变化规律,以期为储气库管柱螺纹接头的优化选择和提高储气库注采管柱密封承载能力提供参考。
1 弹塑性接触基本方程及求解管柱接头金属/金属密封结构的受力分析涉及材料、几何及边界条件等多重非线性,建立精确的数学模型,寻求解析法求解非常困难。目前处理该问题的有效手段是采用有限元分析方法,其本质上属于弹塑性接触问题。根据虚功原理,相互接触的两物体基本方程描述为[8]:

|
(1) |
式中:[K(u)]为整体刚度矩阵,{u}为位移向量,{u}为外载荷向量,{R(u)}为待定接触力向量,{f(u)}为右端项向量。
鉴于承受工作载荷较大,接触面局部应力可能超出材料的屈服极限,考虑材料的弹塑性变形[9],在弹性阶段采用Hooke定理,塑性判据采用Von Mises屈服准则,接头密封结构视为均质金属,屈服后服从Prandtl-Reuss方程,应变增量为:
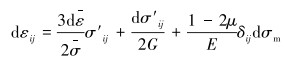
|
(2) |
式中:G为剪切模量,E为弹性模量,μ为泊松比,σ′ij为应力偏量分量,σm为静水压力,σ为等效应力,ε为等效应变,δij为Kronecker符号。
由于式(1)中{R(u)}为未知,尚无法直接求解该方程,须补充接触定解条件和接触状态判定条件,采用增量加载方式进行多次迭代求解。接触点对的接触状态可分为连续、滑动、混合以及分离等4种,不同接触状态下的判定条件和定解条件有所不同[8]。实际求解时,事先不能预知具体状态如何,先假定接触状态,再按这些状态所对应的接触定解条件补充方程后对式(1)求解。接触迭代中,考虑附加刚体位移约束及平衡条件,采用以柔度矩阵为主体的间距协调方程,其增量形式为:

|
(3) |

|
(4) |
式中:F为接触力的柔度矩阵,Fc为位移变换矩阵,ΔSpi(n)为外载增量引起的接触点对相对位移向量,Xi-1(n-1)为当前接触点对间隙,Q为接触力变换矩阵,Δuei(n)为附加刚体位移约束自由度上的位移增量向量,ΔPei(n)为外载增量合力向量。
若需考虑接触表面之间的摩擦力影响,接触点对之间的接触力和接触位移还应再满足附加的约束条件,即有:
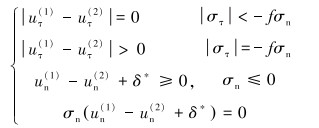
|
(5) |
式中:σn和στ为接触点对的法向和切向接触应力,un(i)和uτ(i)为两个物体在接触点对局部坐标系下的法向、切向相对位移,f为接触表面之间的摩擦因数,δ*为接触初始间隙。
2 注采管柱交变载荷工况储气库每年有几个月的注气和采气过程,气体在管柱和地层之间双向流动,注采压力和流量大且周期变化,同时还受温度变化的影响。压力的交替变化将引起管柱应力及轴向变形的改变,进而导致封隔器或管柱损坏。储气库运行过程中,注采管柱主要承受轴向力、外挤压力和内压力作用。轴向力来自管体自重、鼓胀、活塞、摩阻和温度等效应而产生的力,当累计的这些作用力变化时,需考虑每种效应变化的方向,以便将其所产生的作用力叠加。内压力是注采过程中气体压力直接作用所产生的,注采管柱的载荷工况与一般采气井完井管柱相比,最大的区别是注采管柱的内压力是波动和交替变化的,从而引起外挤压力和轴向力变化。注采管柱通过封隔器坐封在生产套管内,外挤压力和内压力的变化可通过鼓胀效应或活塞效应折算成轴向力[1]。因此,在储气库井注采过程中,可将管柱的交变载荷集中看作轴向的拉伸载荷和压缩载荷。
3 有限元模型建立选取ø139.70 mm×9.17 mm P110钢级的特殊螺纹套管接头为研究对象,建立有限元模型。螺纹部分采用API Spec 5B标准偏梯形螺纹,每英寸5牙。接箍外径为153.67 mm,长度为255 mm。取管体长度大于3倍螺纹段长度建立几何模型,消除端部边界因素的影响。忽略螺旋升角的影响,将接头视为轴对称结构进行建模。接头的主密封结构采取两种不同形式:球面/柱面和锥面/锥面,球面曲率半径取15 mm,密封锥面锥度取1:14,台肩面均采用-15°扭矩台肩结构。主密封面过盈量0.13 mm,台肩面过盈量0.10 mm。
采用plane183平面8节点四边形单元,智能网格划分,设置划分单元大小为0.5 mm,对螺纹牙根部和密封部位进行局部网格细化。划分好后,定义接触关系,接箍表面为目标面,采用targe169单元进行划分;套管表面为接触面,采用conta172单元进行划分。所有划分完成后,总单元数为53 968。套管接头的有限元模型如图 1所示。

|
| 图 1 套管接头有限元模型 Fig.1 Finite element model of casing connection |
材料力学性能参数为:弹性模量210 GPa,泊松比0.3,屈服强度758 MPa,抗拉强度862 MPa,摩擦因数0.02,定义材料模型为多线性随动强化模型。在接箍中面上施加轴对称位移约束,轴向作用力和内压力以分布载荷的形式施加在管体和接箍的内壁及管体端面。
4 密封结构接触压力分析 4.1 交变载荷工况的模拟依据“机紧+内压40 MPa+交变拉压载荷(拉伸取80%VME,压缩取70%VME,30周次拉压循环)”交变工况,其中机紧采用上扣圈数来模拟上扣扭矩(上扣1.5圈),考察受到不同循环周次的轴向拉压交变载荷作用,密封面接触压力的变化情况,拉压交变载荷加载步见图 2。P110钢级套管额定抗拉力为2 853 kN,额定抗内压强度为87.1 MPa。

|
| 图 2 拉压交变载荷加载步(30周次) Fig.2 The alternating axial tension and compression load (30 cycles) |
4.2 仿真结果分析
针对球面/柱面和锥面/锥面两种密封形式进行交变加载计算,交变循环30周次后,将前3周次以及第30周次中处于拉伸和压缩状态的结果进行提取,并做对比分析。
4.2.1 球面/柱面密封结构图 3给出第1、2、3和30周次拉伸及压缩状态下,主密封面上接触压力随接触长度变化的情况。图中横轴主密封面长度表示从台肩端部起沿轴向指向管体螺纹端,纵轴中接触压力值均截取为大于额定抗内压强度。

|
| 图 3 球面/柱面结构主密封面接触压力随接触长度变化曲线 Fig.3 Effect of contact length on the contact stress of primary seal surface of the sphere/cylinder seal structure |
图 4给出第1、2、3和30周次拉伸及压缩状态下,台肩面上接触压力随接触长度变化的情况。图中横轴为台肩面长度,表示从管体内壁沿径向指向台肩顶端。

|
| 图 4 球面/柱面结构台肩面接触压力随接触长度变化曲线 Fig.4 Effect of contact length on the contact stress of shoulder surface of the sphere/cylinder seal structure |
由图 3和图 4可以看出,交变拉伸状态下,不同循环周次主密封面接触压力的大小均呈现一定变化;交变压缩状态下,主密封面和台肩面接触压力几乎不受循环周次的影响。同时,交变压缩作用对主密封和台肩面的接触压力水平有所提升,有利于增强密封性能。
现把不同循环周次主密封面最大接触压力和有效接触长度进行对比(见表 1),发现主密封面最大接触压力从第1周次到第2周次约增加了1.1%,原因在于第1周次中压缩载荷导致密封面有效接触范围内产生了一定的塑性硬化。交变载荷作用下,随着从拉伸到压缩状态的不断转变,主密封面经历最大接触压力从723 MPa到1 131 MPa(相对改变量56.4%)以及有效接触长度从0.30 mm到0.55 mm(相对改变量83.3%)的变化。经过多周次往复交变作用,不免对其密封性能产生一定的负面影响。
| 循环周次 | 最大接触压力/MPa | 有效接触长度/mm | |||
| 拉伸状态 | 压缩状态 | 拉伸状态 | 压缩状态 | ||
| 1 | 715 | 1 131 | 0.30 | 0.55 | |
| 2 | 723 | 1 131 | 0.30 | 0.55 | |
| 3 | 723 | 1 131 | 0.30 | 0.55 | |
| 30 | 723 | 1 131 | 0.30 | 0.55 | |
4.2.2 锥面/锥面密封结构
图 5为第1、2、3和30周次拉抻及压缩状态下,主密封面上接触压力随接触长度变化情况。图 6为1、2、3和30周次拉伸和压缩状态下,台肩面上接触压力随接触长度变化情况。由图可知,锥面/锥面密封结构仅在交变拉伸状态下,不同循环周次主密封及台肩面接触压力发生一定变化,且台肩面接触压力的大小和分布变化更为显著。

|
| 图 5 锥面/锥面结构主密封面接触压力随接触长度变化曲线 Fig.5 Effect of contact length on the contact stress of primary seal surface of the cone/cone seal structure |

|
| 图 6 锥面/锥面结构台肩面接触压力随接触长度变化曲线 Fig.6 Effect of contact length on the contact stress of shoulder surface of the cone/cone seal structure |
同样把锥面/锥面密封结构的不同循环周次主密封面最大接触压力和有效接触长度进行对比(见表 2),发现主密封面最大接触压力从第1周次到第2周次约下降了1.3%,随交变周次增加,最大接触压力基本不再变化。交变载荷作用下,随着从拉伸状态到压缩状态的不断转变,主密封面经历最大接触压力从387 MPa到541 MPa(相对改变量39.8%)以及有效接触长度从0.53 mm到0.73 mm(相对改变量37.7%)的变化。
| 循环周次 | 最大接触压力/MPa | 有效接触长度/mm | |||
| 拉伸状态 | 压缩状态 | 拉伸状态 | 压缩状态 | ||
| 1 | 392 | 541 | 0.53 | 0.73 | |
| 2 | 387 | 541 | 0.53 | 0.73 | |
| 3 | 387 | 541 | 0.53 | 0.73 | |
| 30 | 387 | 541 | 0.53 | 0.73 | |
4.2.3 两种密封结构对比
对比图 3a和图 5a结果,锥面/锥面密封结构密封面有效接触长度较大,球面/柱面密封结构接触压力水平较高,如图 7所示。对比表 1和表 2可知,锥面/锥面密封结构最大接触压力和有效接触长度的相对改变量比球面/柱面结构大幅降低。

|
| 图 7 两种结构形式主密封面上接触压力分布对比(受拉状态) Fig.7 Comparison of contact stress of primary seal surface of the sphere/cylinder and cone/cone seal structures under tensile state |
此外,对比图 4a和图 6a结果,与球面/柱面结构相比,锥面/锥面结构的台肩面接触压力分布较为平坦,表明其辅助密封效果较好,但同时应合理控制其台肩顶端的应力集中问题。因球面/柱面密封结构在主密封面上的有效接触区相对远离台肩,可以适当缓和台肩顶端的应力集中。
综合以上分析,对于管柱接头承受交变载荷而言,当交变载荷循环周次较长(如30周次以上)且承受的轴向力和压力载荷水平较高时,锥面/锥面密封结构的承载效果要好;当交变载荷循环周次较短、载荷水平相对较低时,球面/柱面密封结构的承载效果则更佳。
5 结论及建议(1) 在轴向拉压交变载荷作用下,两种密封结构主密封面上的最大接触压力和有效接触长度随拉伸到压缩状态的不断转变均发生不同程度的改变。经多周次反复作用,将对密封性能产生不利影响,导致密封承载能力有降低的趋势。
(2) 当交变载荷循环周次较长、承受载荷水平较高时,锥面/锥面密封结构的承载效果较好;相反,可采用球面/柱面密封结构。为确保储气库注采管柱在30 a以上长周期安全运行,建议采用锥面/锥面密封结构的气密封螺纹接头。
(3) 锥面/锥面密封形式的有效接触长度相对较长,台肩面辅助密封效果较好,但应合理控制其台肩顶端的应力集中问题。
(4) 研究结果为交变载荷作用下注采管柱接头密封结构的优选和设计提供了参考,建议结合多周次气密封循环试验做进一步的研究。
| [1] |
王建军. 地下储气库注采管柱密封试验研究[J].
石油机械, 2014, 42(11): 170-173.
WANG J J. Seal test of the injection-production string for underground gas storage[J]. China Petroleum Machinery, 2014, 42(11): 170-173. |
| [2] |
黄翠英, 张宏, 段庆全. 地下储气库特殊螺纹套管接头密封性分析[J].
石油机械, 2010, 38(5): 49-51.
HUANG C Y, ZHANG H, DUAN Q Q. Analysis of the sealability of special threaded casing joints in underground gas storage[J]. China Petroleum Machinery, 2010, 38(5): 49-51. |
| [3] |
祝效华, 董亮亮, 童华, 等. 拉弯复合载荷作用下的API短圆套管螺纹力学行为[J].
石油学报, 2013, 34(1): 157-163.
ZHU X H, DONG L L, TONG H, et al. Mechanical behaviors of short-round thread of the API casing under combined load of stretching and bending moment[J]. Acta Petrolei Sinica, 2013, 34(1): 157-163. DOI: 10.3969/j.issn.1001-8719.2013.01.025 |
| [4] |
王建东, 冯耀荣, 林凯, 等. 特殊螺纹接头密封结构比对分析[J].
中国石油大学学报(自然科学版), 2010, 34(5): 126-130.
WANG J D, FENG Y R, LIN K, et al. Comparison analysis of premium connection's seal structure[J]. Journal of China University of Petroleum, 2010, 34(5): 126-130. |
| [5] |
窦益华, 于洋, 曹银萍, 等. 动载作用下特殊螺纹油管接头密封性对比分析[J].
石油机械, 2014, 42(2): 63-65, 72.
DOU Y H, YU Y, CAO Y P, et al. Comparative analysis of the sealability of premium connection under the effect of dynamic load[J]. China Petroleum Machinery, 2014, 42(2): 63-65, 72. DOI: 10.3969/j.issn.1001-4578.2014.02.015 |
| [6] | HAMILTON K, WAGG B, ROTH T. Using ultrasonic techniques to accurately examine seal surface contact stress in premium connections[J]. SPE Drilling and Completion, 2009, 24(4): 696-704. DOI: 10.2118/110675-PA |
| [7] | XIE J R, FENG R, DESSEIN T. Methodology for reliability-based design and assessment of tubular connection sealability in HPHT wells[C]//Proceedings of International Conference on Oil Country Tubular Goods and Tubular String. Canadn: [s.n.], 2014: 9-23. |
| [8] |
李润方, 李剑霞.
接触问题数值方法及其在机械设计中的应用[M]. 重庆: 重庆大学出版社, 1991: 56-63.
LI R F, LI J X. Numerical method of contact problems and its application in mechanical design[M]. Chongqing: Chongqing University Press, 1991: 56-63. |
| [9] |
祝效华, 高原, 贾彦杰. 弯矩载荷作用下偏梯形套管连接螺纹参量敏感性分析[J].
工程力学, 2012, 29(10): 301-307.
ZHU X H, GAO Y, JIA Y J. The parameter sensitivity analysis of buttress casing connecting thread under action of bending loading[J]. Engineering Mechanics, 2012, 29(10): 301-307. |



