2. 江汉石油工程公司工程技术中心
2. Engineering Technology Center, Sinopec Jianghan Oilfield Service Co., Ltd.
0 引言
连续管在石油开发中应用十分广泛,在作业中,作用在连续管上的主要载荷通常有弯曲载荷和内压。由于弯曲半径较小,所以大部分连续管工作在屈服状态,研究加载历史对连续管疲劳的影响非常重要。
为了便于分析,将连续管某一个截面的加载历史归纳为两种:①加内压时卷绕矫直;②卷绕时0内压,停止卷绕时加内压、卸内压,矫直时0内压。这个截面的疲劳损伤与这两种载荷加载历史相关。
关于第一种加载历史国内外已有学者深入研究,国内最具代表性的学者有王优强等[1]、王海涛等[2]、宋生印等[3-7]、毕宗岳等[8-9]、王龙庭等[10-11]、李猛等[12]、朱小平[13]和何春生[14];国外有S.M.TIPTON等[15-16],他们做的研究包括Flexor连续管疲劳试验机以及CTES软件[17-20]。在第一种加载历史连续管的疲劳寿命试验中,连续管加上内压后不断弯曲拉直,直至失效,从而形成失效时连续管的循环次数与内压的关系曲线。关于第二种加载历史目前还没见到相关的研究文献。
为了研究第二种加载历史对连续管本体疲劳寿命的影响,笔者假定疲劳寿命与等效应变幅和等效平均应变有关,提出了一种新的连续管多轴应变到单轴应变幅的等效方式,用修正Manson-Coffin关系式来计算疲劳寿命。具体步骤如下:
(1) 根据第一种加载历史得出的试验结果,结合有限元模拟该加载方式计算每次循环相应的应变,拟合出等效应变幅计算式的各个参数。
(2) 通过有限元模拟第二种加载历史得出的应变,用新的等效关系式计算其疲劳寿命。第二种加载历史除了对连续管本体有影响外,还对斜接焊缝有影响,因此笔者还用有限元方法分析了第二种加载历史对连续管斜接焊缝应变和变形的影响。
1 多轴低周疲劳分析 1.1 基本假设做如下基本假设:
(1) 材料均匀,双线性运动强化,材料的弹性模量、泊松比和切线模量等材料参数在变形过程中不变。
(2) 连续管断面在变形中保持圆形。
(3) 某断面连续管裂纹初始萌发即意味着断面连续管破坏。虽然连续管截面上任意一点破坏并不能立即导致连续管完全失效,但裂纹萌生后会很快扩展,引起连续管截面的整体失效,因此连续管截面上任意一点的破坏被认为连续管发生失效,这时所循环的次数称为连续管的寿命。
(4) 根据Palmgren-Miner损伤线性累加法则,连续管每次循环所受到的损伤会按线性累积起来。一般情况下这种累积是非线性的,已经受到损伤的连续管在同样的载荷循环下,受到的损伤要大于未受损伤连续管,但目前学术界仍采用Palmgren-Miner线性累加法则。
1.2 多轴疲劳的等效分析在单轴疲劳寿命计算中常用Manson-Coffin关系式,即:
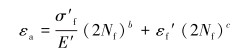
|
(1) |
式中:εa为应变幅;σ′f为疲劳强度系数;b为疲劳强度指数;E′为弹性模量;Nf为弯曲循环次数;ε′f为疲劳延性系数;c为疲劳延性指数。
连续管的载荷特征表明,连续管工作处于多轴疲劳状态,无法用单轴疲劳的关系式描述,一般采用等效办法来描述多轴疲劳状态。S.M.TIPTON[7]采用了如下等效方法:
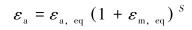
|
(2) |
式中:εa, eq为三轴等效应变幅;εm, eq为三轴平均等效应变;S为应变指数。
对于塑性材料,采用Von Mises等效平均应变和应变幅:
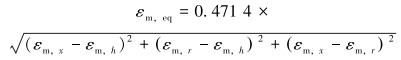
|
(3) |
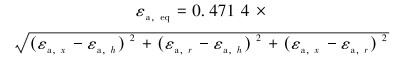
|
(4) |
式中:x、h、r分别表示连续管平均应变和应变幅的轴向、环向及径向分量。
平均应变和应变幅的各分量按式(5)计算:

|
(5) |
式中:下标init和update分别表示每次循环开始和结束,i表示分量x、h和r。
S的表达式为:
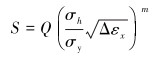
|
(6) |
式中:σy为材料的屈服应力。
这样,Tipton就把连续管多轴疲劳与单轴疲劳的Manson-Coffin关系式联系起来了。但这种等效方法除了等效应变幅和平均等效应变外,还引入了另一个关系式(6)。因此,无法用此等效方法来计算第二种载荷历史时连续管的疲劳寿命。
笔者提出将多轴应变等效到单轴应变幅可用下式计算:
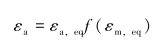
|
(7) |
式中:f(εm, eq)为平均等效应变εm, eq的函数,εa, eq、εm, eq分别按式(3)和式(4)计算。
1.3 疲劳线性损伤累加原理由式(7)可知,不同的εa, eq和εm, eq,等效的εa也不一样,因此所得到的寿命也不一样。为了计算变化应变下的寿命,应用Palmgren-Miner线性损伤累加原理:设第i种等效应变的寿命是2Nfi,则总损伤为:
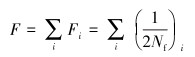
|
(8) |
当某点F =1时,连续管在该点就会发生疲劳失效。因此,计算在某种内压下连续管的寿命,只需要计算每次循环过程中应变分量的值,然后将多轴应变等效到单轴应变幅即可。
2 应变计算模型选择按式(7)将多轴疲劳等效到单轴疲劳,即将多轴应变等效到单轴应变幅,只需要每次循环过程中应变分量的值。
连续管的应力应变计算很难用解析方法比较准确地计算,而用有限元方法比较好。连续管弯曲与矫直,原则上是三维的,因此需要采用三维模型来计算。
2.1 连续管弯曲的三维有限元计算与分析在卷绕到滚筒的过程中,连续管经历了弯曲逐渐增大,最后弯曲到滚筒或靠模上。但矫直时,连续管经历由放松到逐步反向加载直到变直的过程。用三维有限元模拟这一过程,以材料HS-110、外径50.4 mm、壁厚4.445 mm的连续管为例,连续管材料模型为运动强化的Ramberg-Osgood循环应力应变关系:
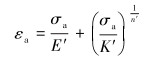
|
(9) |
式中:σa为单轴循环应力,MPa;εa为单轴循环应变;E′为循环弹性模量,MPa;K′为循环强化系数,MPa;n′为循环强化指数。
根据文献[18],材料HS-110的E′=167 149 MPa,K′=898 MPa,n′=0.074 96。
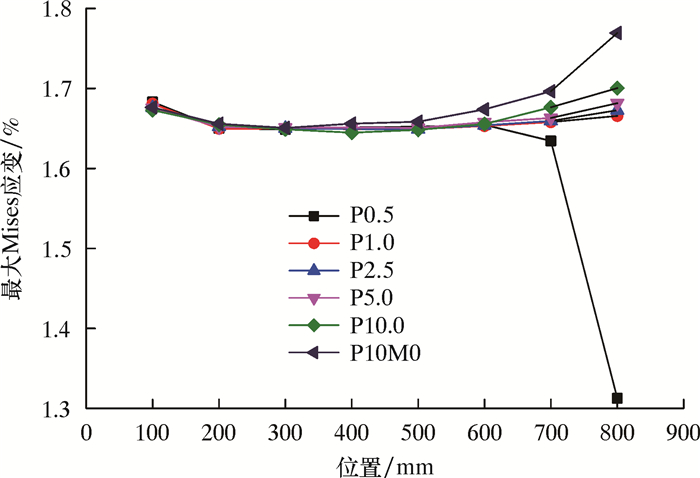
计算卷绕到滚筒上的部分连续管的应变如图 1所示。图中显示,已经卷绕在滚筒上的连续管的应变沿连续管轴线分布均匀。改变端面加载的切向力,重新计算连续管的应变分布,计算的最大Mises应变沿连续管轴线分布如图 2所示。图中P0.5、P1.0和P2.5等分别表示不同端面加载的切向力。从图可以看出,在轴线200~600 mm之间的最大Mises应变比较均匀,认为完全卷绕在滚筒上的连续管沿轴线的不同断面应变分布基本一致,可以简化为广义平面应变来解决。

|
| 图 1 卷绕于滚筒上的连续管应变分布图 Fig.1 Strain distribution of coiled tubing winded roller |
|
| 图 2 不同切向力最大Mises应变沿连续管轴线分布 Fig.2 The maximum Mises strain along the coiled tubing axis under different tangential forces |
2.2 连续管弯曲矫直广义平面应变计算的合理性
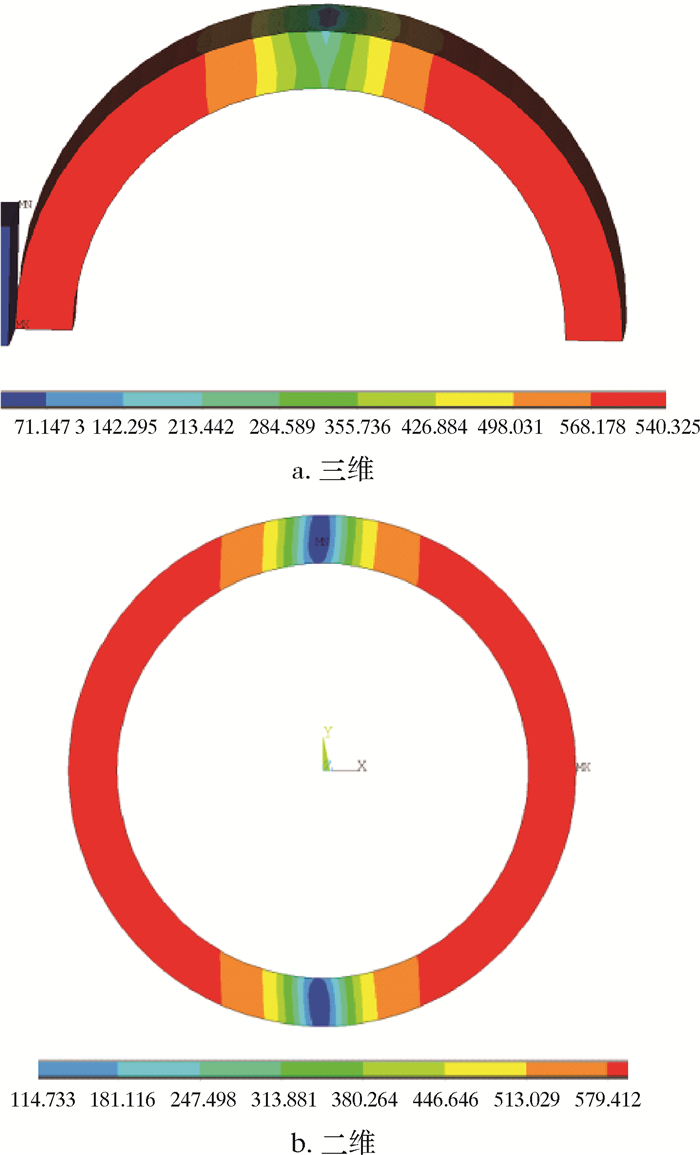
为了进一步验证广义平面应变计算的合理性,用三维模型和二维模型分别对连续管弯曲矫直应力进行计算。三维和二维有限元计算的应力分布如图 3所示。从图可以看出,用三维模型计算的应力与用二维模型计算的应力很接近。
|
| 图 3 三维和二维有限元计算的应力分布 Fig.3 Stress distribution by 3D and 2D finite element calculations |
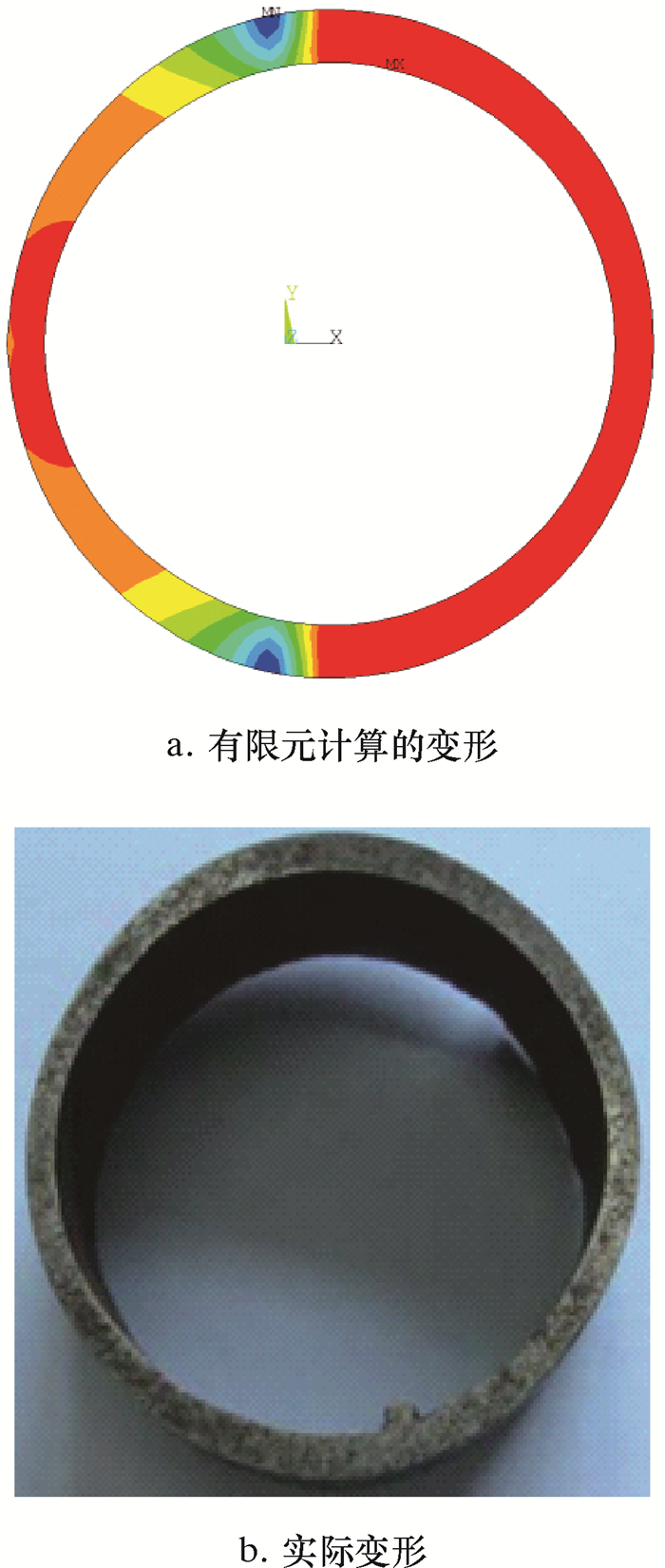
用广义平面应变单元对经过加内压的连续管进行了多次弯曲矫直计算,同时与实际经过多次弯曲矫直的连续管断面变形进行比较,如图 4所示。从图 4可以看出,计算结果与实际变形很接近。
|
| 图 4 广义平面应变有限元计算的变形与实际变形 Fig.4 Comparison between the deformation calculated by generalized plane strain finite element and actual deformation of coiled tubing |
3 应变计算与应变幅拟合 3.1 有限元应变计算
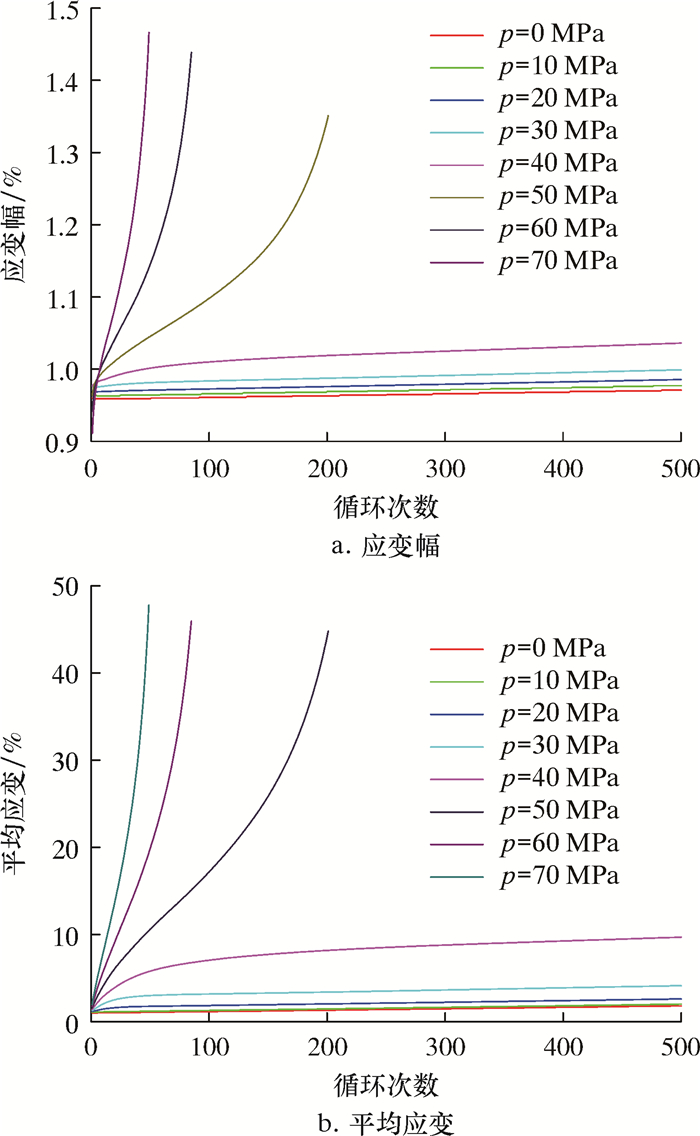
以2.1节所述连续管为例,采用文献[18]的Ramberg-Osgood循环应力应变关系,计算(弯曲半径1 219.2 mm)不同内压p下弯曲时连续管与靠模接触点的等效多轴应变幅和等效多轴平均应变与循环次数的关系,结果如图 5所示。
|
| 图 5 不同内压下连续管与靠模接触点的应变幅与平均应变和循环次数的关系 Fig.5 Relationship between the strain amplitude, the average strain and the number of cycles at the contact point of coiled tubing and bending model under different internal pressures |
从图 5可见,随着内压的增加,连续管应变幅和平均应变随循环次数增长,应变幅增长得慢,平均应变增长得快。
3.2 计算步骤与拟合结果拟合疲劳试验曲线的过程如下:
(1) 用二维广义平面应变问题计算不同内压下连续管弯曲的应力应变。
(2) 计算不同内压下连续管弯曲矫直的应力应变。
(3) 计算各应变幅εa分量以及平均应变εm分量。
(4) 由每次循环的应变幅分量和平均应变分量计算等效应变幅εa, eq和等效平均应变εm, eq。
(5) 试选f(εm, eq),根据式(7)计算等效到单轴应变幅εa的值,再用式(1)计算每次循环等效应变下的寿命。
(6) 根据式(8)计算每次循环的损伤,当累加损伤等于1时,连续管失效。
式(1)中σ′f=1 319.565 1 MPa, b=-0.120 55, εf′=0.570 65, c=-0.745 59[18],利用文献[21]中连续管弯曲的试验数据,式(7)可以拟合为:
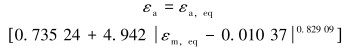
|
(10) |
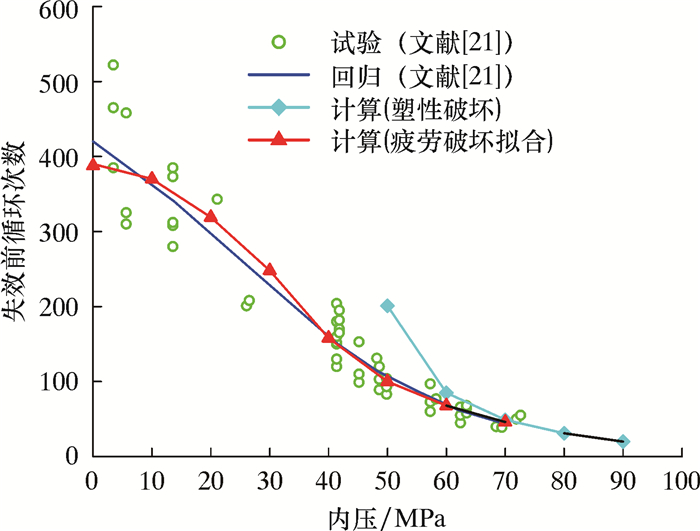
图 6是用本方法计算的连续管寿命与试验拟合曲线的对比。从图 6可以看出,在高内压下(70 MPa以上),连续管是塑性破坏而非疲劳破坏;低内压是疲劳破坏;在中压时计算结果与试验拟合曲线比较接近。
|
| 图 6 计算的连续管寿命与试验拟合曲线对比 Fig.6 Comparison between the calculated coiled tubing life and the experimental fitting curve |
4 本体卷绕后加载卸载内压对连续管疲劳寿命的影响
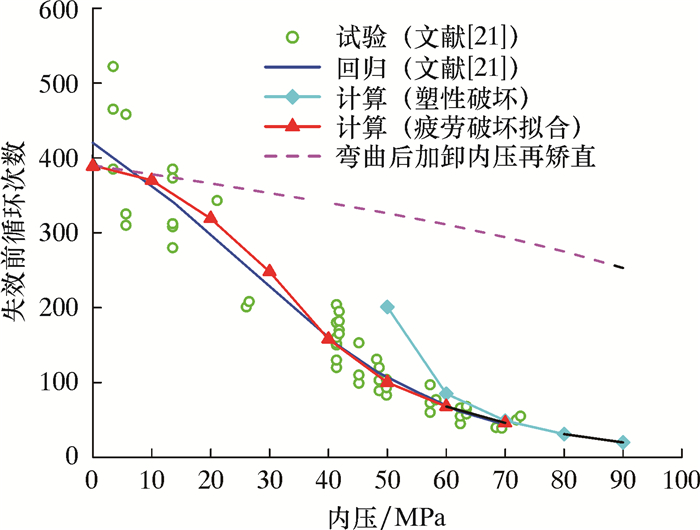
按照先弯曲、再加内压卸内压、再矫直的加载方式,用广义平面应变单元计算连续管与靠模接触点的应变幅和平均应变,再通过拟合式(10),将应变幅和平均应变等效为对称循环的应变幅,最后用Palmgren-Miner线性累加法则计算每次循环的损伤,损伤等于1就意味着连续管疲劳破坏。计算曲线、试验数据和拟合结果如图 7所示,其中虚线为本体弯曲后加卸载内压再矫直的寿命曲线。从图 7可以看出,这种加载方式对连续管本体影响不大。静止加卸载内压90 MPa寿命仍有253次,但90 MPa内压下弯曲矫直只有20次。
|
| 图 7 第二种次序加载疲劳寿命与内压的关系 Fig.7 The relationship between the fatigue life calculated by using the second loading sequence and internal pressure |
5 斜接焊缝卷绕后加载卸载内压对连续管疲劳寿命的影响 5.1 斜接焊缝热影响区(HAZ)
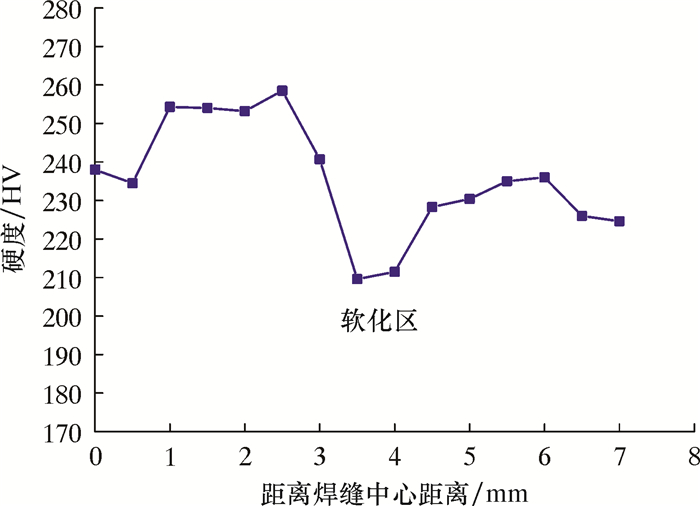
连续管都是由几百米长的钢带通过斜接焊缝连接成几千米长的钢带经卷制焊接而成。在进行斜接焊缝焊接时,焊缝的温度达到钢材的熔点以上,钢材的再结晶温度要低于熔点,这样会在焊缝热影响区(HAZ)形成退火,使材料性能变差,硬度降低,如图 8所示的软化区,屈服强度和抗拉强度也会相应降低。
|
| 图 8 焊接后焊缝周边热影响区的硬度分布 Fig.8 Hardness distribution of the heat affected zone around the weld after welding |
5.2 焊缝热影响区对连续管寿命的影响分析
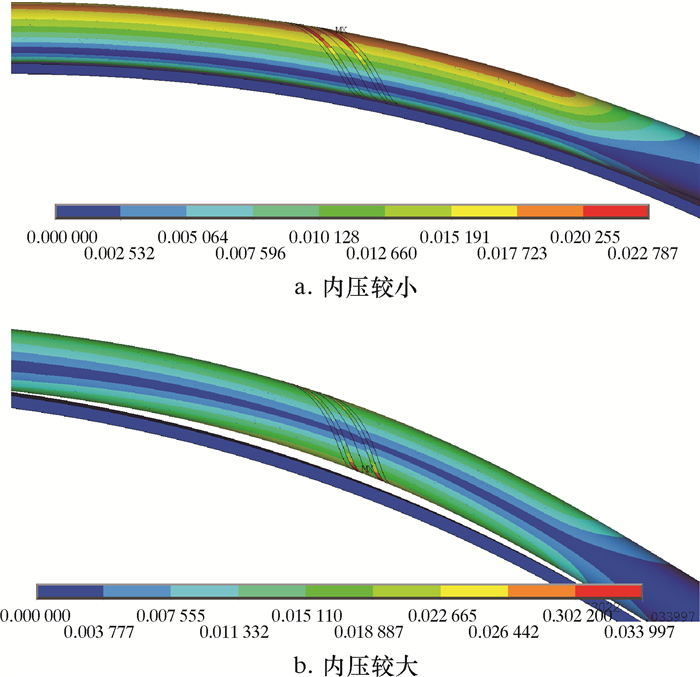
假设HAZ的屈服应力降低5%,对HS-110钢级带斜接焊缝的连续管卷绕在滚筒上加卸内压的工况进行计算。弯曲在滚筒上加内压,当内压较小时,连续管仍然在滚筒上,如图 9a所示;当内压加大到一定程度,连续管会出现翘起现象,如图 9b所示。
|
| 图 9 卷绕于滚筒上加内压时焊缝热影响区对连续管变形的影响 Fig.9 Effect of weld heat affected zone on deformation of coiled tubing winded on roller under internal pressure |
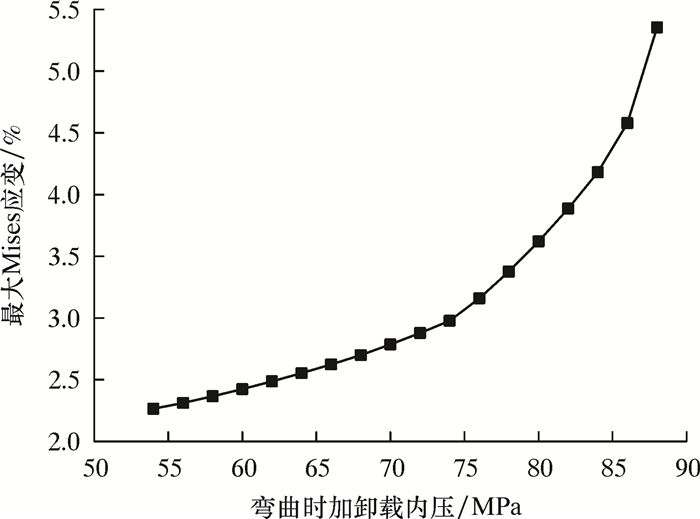
连续管出现翘起现象会使焊缝热影响区的应变增加,如图 10所示。当内压加到50 MPa以上时,连续管开始翘起,再继续增加内压到75 MPa,会出现应变增加较快的情况,如果增加到88 MPa,焊缝热影响区的应变迅速增加会导致连续管破坏。但连续管是逐层卷绕,上层对下层有约束作用,会限制连续管的翘起,卷绕时连续管的规律排列也可以减小翘起带来的影响,因此会减小最大Mises应变。
|
| 图 10 连续管卷绕在滚筒上逐步加内压时斜接焊缝的最大Mises应变 Fig.10 The maximum Mises strain of the helical weld in the coiled tubing winded on the roller with the gradually increased internal pressure |
6 结论
(1) 提出了将连续管的多轴疲劳等效成单轴疲劳,进而采用Manson-Coffin关系式进行疲劳寿命计算的新方法。该方法比文献[7]的方法更简单,只需要计算出应变分量,就可求出连续管的疲劳寿命。因此,根据连续管保持内压弯曲矫直得出的试验寿命曲线,就可以通过有限元计算应变再应用于连续管弯曲状态下加卸载内压再矫直的寿命估算,从而减少了试验次数,降低了成本。
(2) 连续管弯曲状态下加内压和卸内压再矫直对连续管本体寿命有一定影响,但影响不大。
(3) 卷绕后加载卸载内压对连续管的斜接焊缝应变影响较大,建议卷绕后加载卸载内压的最大值不超过75 MPa,特殊情况下不超过85 MPa。
(4) 卷绕时连续管排列整齐有利于减少连续管卷绕到滚筒后加载的高内压对其斜接焊缝的损伤。
| [1] |
王优强, 张嗣伟. 连续油管疲劳寿命预测模型的建立[J].
青岛建筑工程学院学报, 2001, 22(1): 1-5.
WANG Y Q, ZHANG S W. The prediction model of the coiled tubing fatigue life[J]. Journal of Qingdao Institute of Architecture and Engineering, 2001, 22(1): 1-5. DOI: 10.3969/j.issn.1673-4602.2001.01.001 |
| [2] |
王海涛, 李相方. 连续油管卷曲低周疲劳寿命预测[J].
石油机械, 2008, 36(11): 25-27, 31.
WANG H T, LI X F. Prediction of low cycle fatigue life of curling coiled tubing[J]. China Petroleum Machinery, 2008, 36(11): 25-27, 31. |
| [3] |
宋生印, 王英杰, 林元华, 等. 连续管疲劳寿命预测[J].
煤田地质与勘探, 2006, 34(6): 73-76.
SONG S Y, WANG Y J, LIN Y H, et al. Fatigue life estimate for coiled tubing[J]. Coal Geology & Exploration, 2006, 34(6): 73-76. DOI: 10.3969/j.issn.1001-1986.2006.06.022 |
| [4] |
高霞, 上官丰收, 宋生印. 连续管低周疲劳试验装置方案分析[J].
石油矿场机械, 2007, 36(11): 63-67.
GAO X, SHANGGUAN F S, SONG S Y. The low-cycle fatigue testing equipment program analysis of coiled tubing[J]. Oil Field Equipment, 2007, 36(11): 63-67. DOI: 10.3969/j.issn.1001-3482.2007.11.020 |
| [5] |
宋生印, 王英杰, 高霞, 等. 连续管疲劳实验装置研制和实物实验研究[J].
科技导报, 2008, 26(14): 66-71.
SONG S Y, WANG Y J, GAO X, et al. Development of fatigue life test equipment and full-size test for coiled tubing[J]. Science & Technology Review, 2008, 26(14): 66-71. DOI: 10.3321/j.issn:1000-7857.2008.14.012 |
| [6] |
李磊, 王鹏, 申昭熙, 等. 连续管在内压和循环弯曲作用下的试验研究[J].
石油机械, 2011, 39(1): 5-7, 12.
LI L, WANG P, SHEN Z X, et al. An experimental study of the coiled tubing under the effect of internal pressure and cyclic bending[J]. China Petroleum Machinery, 2011, 39(1): 5-7, 12. |
| [7] |
高霞, 肖国章. 连续油管低周疲劳分析[J].
焊管, 2012, 35(4): 32-36.
GAO X, XIAO G Z. Analysis on low cycle fatigue of coiled tubing (CT)[J]. Welded Pipe & Tube, 2012, 35(4): 32-36. DOI: 10.3969/j.issn.1001-3938.2012.04.007 |
| [8] |
毕宗岳, 井晓天, 何石磊, 等. 基于大应变下CT80连续管疲劳寿命研究[J].
热加工工艺, 2010, 39(22): 19-22.
BI Z Y, JING X T, HE S L, et al. Study on fatigue life of CT80 grade coiled tube based on large strain[J]. Material & Heat Treatment, 2010, 39(22): 19-22. DOI: 10.3969/j.issn.1001-3814.2010.22.006 |
| [9] |
毕宗岳, 张晓峰, 张万鹏. 连续管疲劳寿命实验研究[J].
焊管, 2012, 35(6): 5-8.
BI Z Y, ZHANG X F, ZHANG W P. Experimental study on fatigue life of coiled tubing[J]. Welded Pipe & Tube, 2012, 35(6): 5-8. DOI: 10.3969/j.issn.1001-3938.2012.06.001 |
| [10] |
王龙庭.钻井连续管力学特性研究[D].东营: 中国石油大学(华东), 2008. WANG L T. Mechanical analysis of coiled tubing for drilling[J]. Dongying: China University of Petroleum(Huadong), 2008. http://cdmd.cnki.com.cn/article/cdmd-10615-2006146214.htm |
| [11] |
王龙庭, 徐兴平. 连续管工作寿命预分析[J].
石油矿场机械, 2007, 36(12): 55-58.
WANG L T, XU X P. Pre-analysis of coiled tubing working life[J]. Oil Field Equipment, 2007, 36(12): 55-58. DOI: 10.3969/j.issn.1001-3482.2007.12.017 |
| [12] |
李猛, 贺会群, 苏堪华, 等. 连续管定向工具工作原理及工具面角度调整分析[J].
钻采工艺, 2017, 40(1): 7-10.
LI M, HE H Q, SU K H, et al. Working principle of coiled tubing orienter and analysis on tool face orientation[J]. Drilling & Production Technology, 2017, 40(1): 7-10. DOI: 10.3969/J.ISSN.1006-768X.2017.01.02 |
| [13] |
朱小平. 连续油管卷绕弯曲寿命分析[J].
钻采工艺, 2000, 23(6): 51-53.
ZHU X P. Analysis of fatigue life of bending coiled tubing[J]. Drilling & Production Technology, 2000, 23(6): 51-53. |
| [14] |
何春生.连续管低周疲劳寿命预测及屈曲分析方法研究[D].大庆: 东北石油大学, 2014. HE C S. The prediction of low cycle fatigue life and study of buckling analysis method for coiled tubing[D]. Daqing: Northeast Petroleum University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10220-1014390486.htm |
| [15] | TIPTON S M. Multiaxial plasticity and fatigue life prediction in coiled tubing, fatigue lifetime predictive techniques[M].[s.l.]: American Society for Testing and Materials, 1996: 283-304. |
| [16] | CHRISTIAN A, TIPTON S M. Statistical analysis of coiled tubing fatigue data[R]. SPE 121457, 2009. |
| [17] | TIPTON S M. CT fatigue life prediction algorithm[OL]. 1999. http://zh.scribd.com/doc/92492893/Achilles-Fatigue-Model. |
| [18] | TIPTON S M. CT fatigue life prediction algorithm[OL]. 2003. http://120.52.72.37/ctes.nov.com/c3pr90ntcsf0/Documentation/technotes/Tech%20Note%20Achilles%20Fatigue%20Model.pdf |
| [19] |
明瑞卿, 贺会群, 唐纯静, 等. 国内外连续管软件分析[J].
石油钻采工艺, 2017, 39(6): 771-780, 794.
MING R Q, HE H Q, TANG C J, et al. Study and analysis on domestic and foreign software related with coiled tubing[J]. Oil Drilling & Production Technology, 2017, 39(6): 771-780, 794. |
| [20] |
李银银, 周志宏, 臧传贞, 等. 连续管卷绕破坏分析[J].
石油机械, 2015, 43(10): 81-85.
LI Y Y, ZHOU Z H, ZANG C Z, et al. Analysis of coiled tubing failure caused by winding[J]. China Petroleum Machinery, 2015, 43(10): 81-85. |
| [21] | VALDEZ M, MORALES C, REICHERT B. The development of high-strength coiled tubing with improved fatigue performance and H2S resistance[R].SPE-173639-MS, 2015. |



