0 引言
连续管技术已广泛应用于油气田钻井(侧钻)、完井、压裂和修井等作业中,取得了显著的效果。在大多数作业中,连续管处于井下复杂应力环境中,容易使其综合性能逼近材料性能极限,出现井下塑性挤毁、管体破裂、疲劳断裂和塑性屈曲等失效事故。连续管的强度极限决定其承受复杂应力的能力大小,其强度极限的研究和计算是一项极其重要的工作。一般来说,每一种井下事故都可能涉及连续管不同的性能极限,如抗挤强度、抗内压强度、塑性极限、抗拉强度、疲劳寿命极限、直径及椭圆度极限等。这些性能极限通常相互影响,但也可结合具体工况独立考虑和讨论。例如,连续管环空压裂过程中,其外部压力远高于内部压力,再加之其所受轴向力及弯曲应力等耦合载荷,很可能使连续管外壁首先达到材料屈服极限,在外壁发生屈服后,最终可能造成连续管屈服失效和塑性挤毁。
关于连续管的性能极限问题,国内外学者进行了大量研究。K.R.NEWMAN等[1-2]考虑连续管的残余应力及弯矩,分析了连续管从滚筒到鹅颈架弯曲、拉直释放过程中残余应力的变化及拉伸强度;Y.S.YANG[3-4]基于弹性失稳原理分析了轴向拉力作用下连续管的抗挤强度和抗内压强度;K.R.NEWMAN等[5]分析了连续管的疲劳寿命;S.M.TIPTON[6]分析了循环弯曲应力和应变作用下连续管直径增长和伸长变形;L.LI等[7]分析了内压和轴向载荷对连续管变形及椭圆度的影响;M.DAVORIN和刘清友等[8-9]分析了连续管的应力分布。虽然上述文献在连续管抗挤强度、抗内压强度、拉伸极限和直径增长等方面取得了一定的认识,但针对复杂应力状态下连续管的失效机理研究不足,特别是轴向压力对连续管抗挤强度的影响分析不足。此外,连续管强度极限研究中的一个关键问题是选择合适的屈服准则,因为选用不同的屈服准则会得到不同的强度极限。长期以来,国内外大多数学者对连续管的强度极限分析主要采用Von Mises屈服准则和Tresca屈服准则。Tresca屈服准则忽略了中间主应力对材料屈服和结构强度的影响,它所确定的强度极限导致了保守的预测和设计。Von Mises屈服准则由于其非线性的数学表达而导致数学上求解困难,同时也没有考虑材料的SD效应。
在工程结构强度分析中,双剪统一强度理论的应用尤为广泛,它弥补了Tresca屈服准则和Von Mises屈服准则的不足,同时考虑了3个主应力的影响,并能通过中间主应力系数反映中间主应力对材料屈服强度的影响程度,能充分发挥材料的强度潜力,其计算结果具有较高的稳定性和可靠性。因此,笔者根据双剪统一强度理论,考虑井下屈曲、轴向力及内压等因素,对复杂应力状态下连续管的抗挤强度进行分析,并提出连续管强度设计的可行性建议,以期为不同工况下连续管的安全应用和强度预测提供理论依据。
1 连续管的复杂应力 1.1 径向应力和环向应力在内压pi和外压po联合作用下,连续管的径向应力和环向应力为[10]:
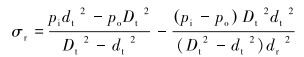
|
(1) |

|
(2) |
式中:pi为连续管内压力,MPa;po为连续管环空压力,MPa;Dt为连续管外径,mm;dt为连续管内径,mm;dr为连续管筒壁内任一点的直径,mm。
1.2 轴向应力在拉伸载荷作用下,连续管的轴向应力为(拉应力):
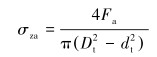
|
(3) |
式中:σza为连续管的轴向拉应力,MPa;Fa为连续管的轴向力,kN。
当轴向力Fa<0且大于连续管的临界屈曲载荷时,连续管在井下发生正弦或螺旋屈曲,由屈曲引起的附加弯矩为:
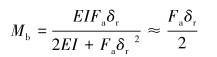
|
(4) |
式中:Mb为连续管屈曲产生的弯矩,N·m;E为连续管钢材弹性模量,MPa;I为连续管横截面的惯性矩,mm4,
连续管屈曲引起的附加轴向弯曲应力(拉为正,压为负)为:

|
(5) |
由于井下屈曲的影响,连续管弯曲凸起的一侧受附加弯曲拉应力,凹进的一侧受附加弯曲压应力。连续管受压时,最大轴向应力在弯曲应力产生压应力的一侧,则连续管总的轴向应力为:
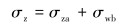
|
(6) |
将式(3)和式(5)代入式(6),得合成轴向应力(压应力)σz为:
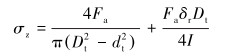
|
(7) |
双剪统一强度理论是一种对于材料的拉压异性和同性、不同中间主应力效应以及能够适用于不同屈服准则的一种强度理论。双剪统一强度理论的统一表达式为[11]:
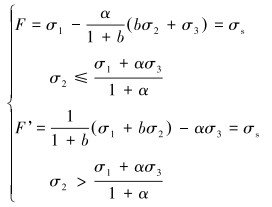
|
(8) |
式中:b为反映中间主应力影响的系数,且0≤b≤1;α为材料的拉伸极限强度与压缩极限强度之比;σs为连续管管材的屈服强度,MPa。
当α和b取不同值时,双剪统一强度理论可退化为不同的强度屈服准则。当α=1,b=0.0、0.5和1.0时,可以得到Tresca屈服准则(即单剪屈服准则)、线性逼近的Von Mises屈服准则(即三剪屈服准则)和双剪应力屈服准则。
2.2 抗挤强度模型根据双剪统一强度理论,在径向应力σr、环向应力σθ和轴向应力σz这3向复杂主应力作用下,当连续管的等效应力达到连续管管材的屈服强度σs时,连续管将发生屈服破坏。根据分析,当po>pi时,最大应力点发生在连续管的外表面,使连续管的外壁首先发生屈服。因此,确定连续管抗挤强度时应该考虑连续管外壁的屈服。
由于轴向应力σz是独立的,且可以为压应力和拉应力,同时径向应力σr始终小于0,环向应力σθ也小于0,这3种主应力在实际工况中可能出现2种情况:①轴向应力为拉应力,即σz≥0,则3个主应力排序只可能为σz≥σr≥σθ;②轴向应力为压应力,即σz<0,则3个主应力排序可能为σz≥σr≥σθ、σr≥σz≥σθ或σr≥σθ≥σz。因此,需要分析上述2种条件下连续管外壁初始屈服的抗挤强度。
当dr=Dt时,式(1)和式(2)可改写为:
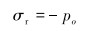
|
(9) |
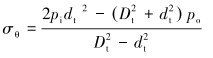
|
(10) |
为便于分析,引入无因次量:
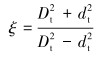
|
(11) |
则式(10)可简化为:
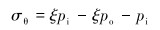
|
(12) |
设σz≥0,有σ1=σz,σ2=σr,σ3=σθ。如果
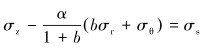
|
(13) |
将式(9)、式(12)代入式(13),得连续管的抗挤强度poe为:
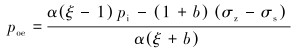
|
(14) |
如果
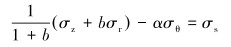
|
(15) |
将式(9)、式(12)代入式(15),得连续管的抗挤强度poe为:
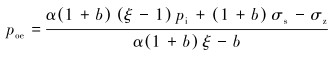
|
(16) |
设σz<0,则有σ1=σz,σ2=σr,σ3=σθ。如果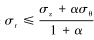
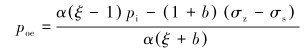
|
(17) |
若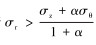
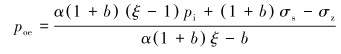
|
(18) |
设σz<0,则有σ1=σr,σ2=σz,σ3=σθ。当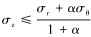
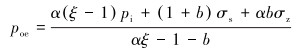
|
(19) |
当
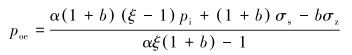
|
(20) |
设σz<0,则有σ1=σr,σ2=σθ,σ3=σz。当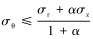
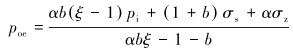
|
(21) |
当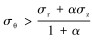
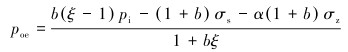
|
(22) |
推导出的轴向拉应力和轴向压应力条件下连续管抗挤强度的计算模型,为复杂应力状态下连续管抗挤强度的计算提供了理论依据。
3 敏感性分析及结果讨论以ø50.8 mm×3.96 mm(2 in×0.156 in)的QT900连续管为例,在拉压同性材料(α=1)的基础上,选用双剪统一强度理论3个典型的参数b=0.0、b=0.5和b=1.0,对比分析不同轴向力和内压作用下该连续管的抗挤强度。
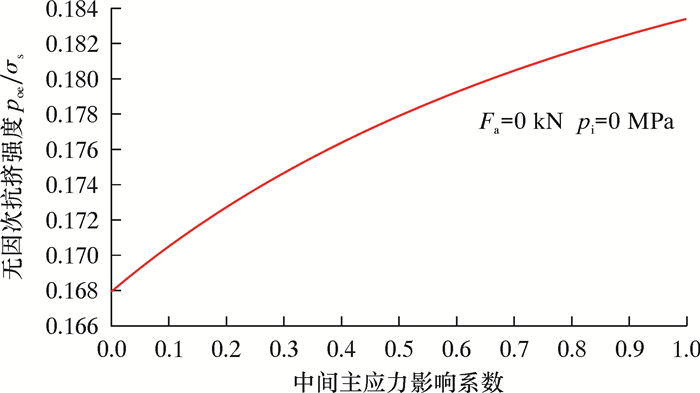
在轴向拉应力(σz≥σr≥σθ)条件下,QT900连续管的抗挤强度与中间主应力影响系数b的关系如图 1所示。由图可以看出,对于拉压同性材料,当取不同的参数b时,双剪统一强度理论将得到不同的无因次抗挤强度(poe/σs)。这表明双剪统一强度理论的应用将在不同程度上提高连续管的抗挤强度。
|
| 图 1 连续管抗挤强度与中间主应力影响系数的关系 Fig.1 Relationship between the collapse strength of coiled tubing and the influence coefficient of intermediate principal stress |
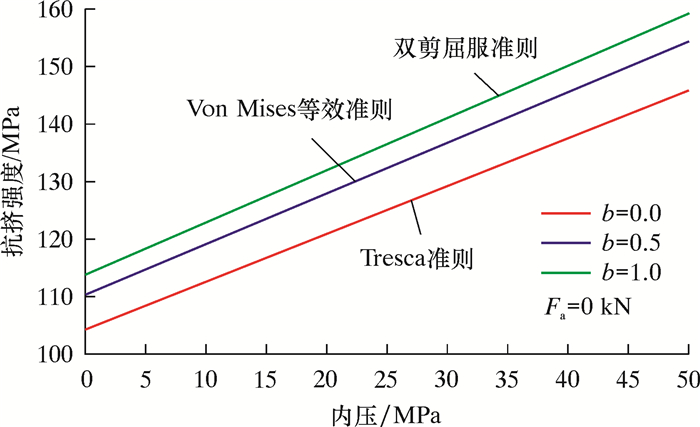
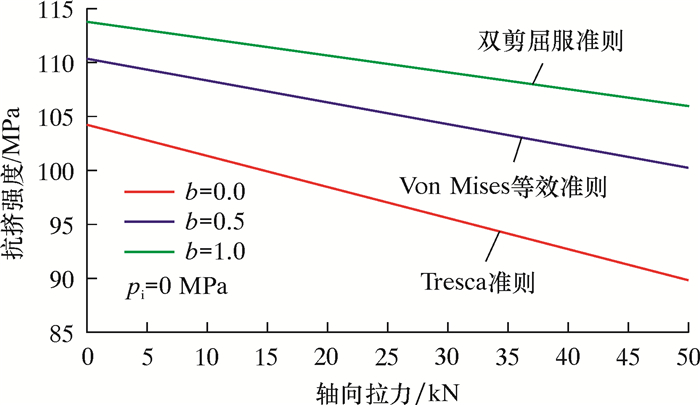
轴向拉应力(σz≥σr≥σθ)条件下,QT900连续管的抗挤强度随内压和轴向拉力的变化分别如图 2和图 3所示。
|
| 图 2 连续管抗挤强度随内压变化曲线 Fig.2 Effect of internal pressure on the coiled tubing collapse strength |
|
| 图 3 连续管抗挤强度随轴向拉力变化曲线 Fig.3 Effect of axial tensile force on the coiled tubing collapse strength |
由图 2和图 3可以看出,连续管的抗挤强度随内压的增加而增大,这说明在一定程度上内压对提高连续管的抗挤强度具有积极作用。连续管的抗挤强度随轴向拉力的增加而减小,这表明轴向拉力对连续管的抗挤强度具有削弱作用。双剪统一强度理论在b=0.0时的计算结果与Tresca屈服准则计算结果相同,这说明双剪统一强度理论包含了Tresca屈服准则。同时,双剪统一强度理论(b=0.5)也包含了线性逼近的Von Mises等效屈服准则。因此,采用双剪统一强度理论推导的连续管抗挤强度计算模型正确,而且该模型(b=1.0)显著提高了连续管的抗挤强度。建议实际工程应用中,采用双剪统一强度理论的计算模型进行强度设计。
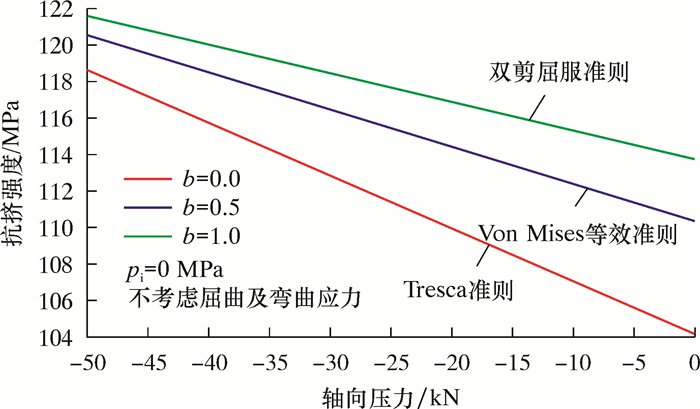
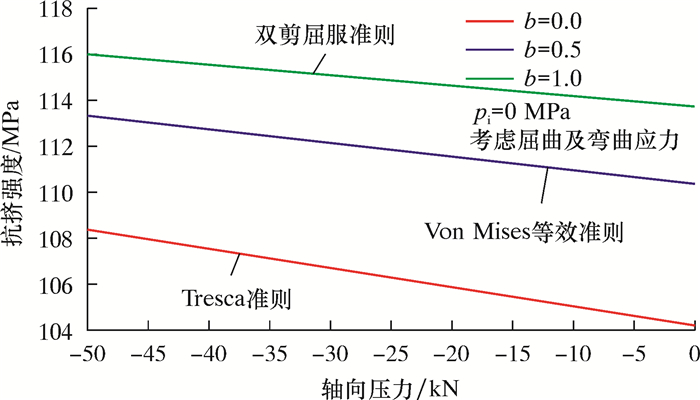
轴向压应力(σz≥σr≥σθ)条件下,考虑和不考虑屈曲及弯曲应力时,QT900连续管的抗挤强度随轴向压力的变化分别如图 4和图 5所示。由图可以看出,不考虑屈曲及弯曲应力时,随着轴向压力的增加,连续管的抗挤强度变大。考虑屈曲及弯曲应力后,连续管的抗挤强度比不考虑屈曲时小;轴向压力越大,考虑屈曲及弯曲应力时,连续管的抗挤强度比不考虑屈曲时小得越多。因此,不考虑井下屈曲及附加弯曲应力的影响分析连续管的抗挤强度不合适。
|
| 图 4 不考虑屈曲时连续管抗挤强度随轴向压力变化曲线 Fig.4 Effect of axial compressive force on coiled tubing collapse strength without considering buckling |
|
| 图 5 考虑屈曲时连续管抗挤强度随轴向压力变化曲线 Fig.5 Effect of axial compressive force on coiled tubing collapse strength considering buckling |
4 模型验证
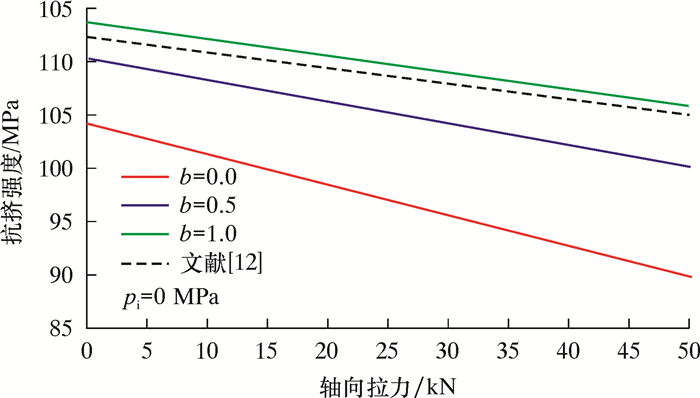
为了验证复杂应力状态下连续管抗挤强度模型的可靠性,用现有理论模型进行对比和评价。文献[12]基于连续管外表面的初始屈服,考虑连续管的三轴应力,根据Von Mises屈服判据推导了连续管的抗挤强度模型。在轴向拉应力(σz≥σr≥σθ)条件下,QT900连续管抗挤强度的统一强度理论模型与现有理论模型对比如图 6所示。由图可以看出,采用笔者提出的模型(b=0.5和b=1.0)计算的连续管抗挤强度与现有理论模型计算结果非常接近。这表明,基于双剪统一强度理论建立的复杂应力状态下连续管抗挤强度模型可以较好地描述井下连续管的力学行为。建议实际工程应用中,采用笔者提出的模型进行连续管的抗挤强度设计。
|
| 图 6 连续管抗挤强度的统一强度理论模型与现有模型对比 Fig.6 Unified strength model of coiled tubing collapse strength versus current model |
5 结论及建议
(1) 基于双剪统一强度理论建立的连续管抗挤强度计算模型可以较好地描述井下连续管的力学行为,为连续管的强度设计和失效分析提供了实用的理论新模型。
(2) 应用双剪统一强度理论,当其中间主应力影响系数b取不同值时,就能获得按Tresca准则、线性逼近的Von Mises准则和双剪应力准则进行计算的弹性解。
(3) 随着轴向拉力的增加,连续管的抗挤强度减小;不考虑屈曲及弯曲应力时,随着轴向压力的增加,连续管的抗挤强度增大。
(4) 考虑屈曲及弯曲应力后,连续管的抗挤强度比不考虑屈曲时小;轴向压力越大,考虑屈曲及弯曲应力时,连续管的抗挤强度比不考虑屈曲时小得越多。因此,应该考虑井下屈曲及弯曲应力的影响来分析连续管的抗挤强度。
(5) 双剪统一强度理论可以为不同工况下油井管的强度设计和失效分析提供一种新方法,建议将该方法应用到实际工程中。
| [1] | NEWMAN K R. Coiled tubing pressure & tension limits[R]. SPE 23131, 1991: 269-276. |
| [2] | NEWMAN K R, STONE L R, WOLHART S. Defining coiled tubing limits a new approach[R]. OTC 8221, 1996: 647-655. |
| [3] | YANG Y S. Collapse pressure of coiled tubing under axial tension[R]. SPE 36338, 1997: 177-181. https://www.onacademic.com/detail/journal_1000035598131310_03d7.html |
| [4] | YANG Y S. Collapse and burst pressure of coiled tubing under tension load[J]. Bulletin of Precision Tube Technology, 1995, 1(1): 126-130. |
| [5] | NEWMAN K R, NEWBURN D A. Coiled tubing life modeling[R]. SPE 22820, 1991: 347-351. |
| [6] | TIPTON S M. Coiled tubing deformation mechanics: diametral growth and elongation[R]. SPE 36336, 1998: 194-199. |
| [7] | LI L, SHEN Z X, WANG P. Mechanism study on the coiled tubing deformation under a combination loading[J]. Advanced Materials Research, 2011, 1442(328): 1528-1532. |
| [8] | DAVORIN M, Gaurina-međimurec N, Krištafor Z. Developemnt of coiled tubing stress analysis[J]. Rudarsko-Geološko-Naftni Zbornik, 1998, 1(10): 77-81. |
| [9] |
刘清友, 瞿丹, 祝效华, 等. 连续管夹持力学模型初探与有限元分析[J].
石油机械, 2011, 39(12): 45-48.
LIU Q Y, QU D, ZHU X H, et al. The research of the continuous pipe clamping force model and finite element analysis[J]. China Petroleum Mechinery, 2011, 39(12): 45-48. |
| [10] |
刘鸿文.
材料力学(Ⅱ)[M]. 北京: 高等教育出版社, 2004: 147-158.
LIU H W. Mechanics of materials (Ⅱ)[M]. Beijing: Higher Education Press, 2004: 147-158. |
| [11] | KOLUPAEV V A, YU M H, ALTENBACH H. Visualization of the unified strength theory[J]. Archive of Applied Mechanics, 2013, 83: 1061-1085. DOI: 10.1007/s00419-013-0735-8 |
| [12] |
王优强, 张嗣伟. 连续管的挤毁压力分析[J].
石油矿场机械, 1999, 28(2): 37-40.
WANG Y Q, ZHANG S W. The analysis of coiled tubing collapse pressure[J]. Oil Field Equipment, 1999, 28(2): 37-40. DOI: 10.3969/j.issn.1001-3482.1999.02.012 |



