2. 中国石油大学(北京)
2. China University of Petroleum(Beijing)
0 引言
深水油气井环空圈闭压力是指由于套管环空流体受温度升高的影响而膨胀,从而使密闭环空产生附加压力的现象[1-2]。在陆上油田和浅海油田的勘探开发中,一旦出现圈闭压力,可以通过打开地面套管头侧翼阀的方法释放套管环空圈闭压力。然而,由于深水油气井受限于水下井口,密闭环空没有释放压力的通路[3-4],从而形成附加圈闭压力,威胁井筒安全。例如1999年,墨西哥湾Marlin油田的几口深水井,在生产数小时后,套管环空流体温度和压力明显升高,导致套管严重破坏[5]。因此,对油气井测试和生产过程中套管环空圈闭压力的研究至关重要。笔者基于深水井井身结构和井筒传热过程,通过计算深水钻完井套管环空温度分布,建立了套管环空压力的预测模型,提出了利用牛顿下山法求解环空压力的方法,并利用现场实例对所建模型进行了验证。所得结论可为深水油气井环空圈闭压力的计算提供理论指导。
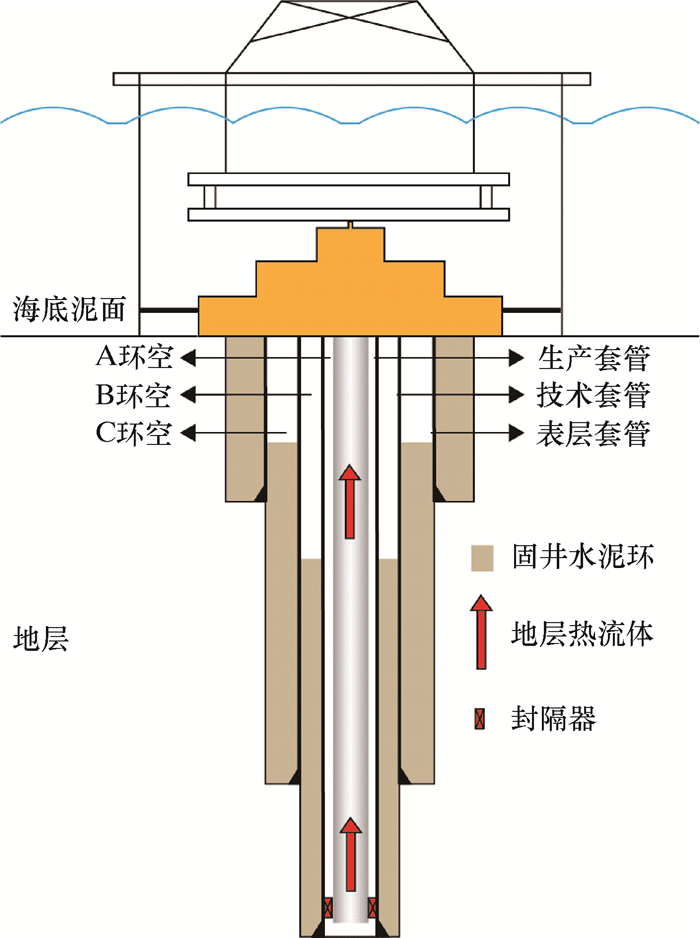
1 物理模型深水油气井常常为水下井口,套管层次较多,油气开采或测试过程中套管环空温度升高形成环空圈闭压力。图 1为典型深水井井身结构及井筒热传递示意图。图中,A环空为测试管柱与生产套管之间的环空,B环空为生产套管与技术套管间未被水泥浆封固段的环空,C环空为技术套管与表层套管间未被水泥浆封固段的环空。
|
| 图 1 深水井身结构及井筒热传递示意图 Fig.1 Schematic diagram of deepwater wellbore configuration and wellbore heat transfer |
2 数学模型 2.1 假设条件
参照文献[6]和文献[7],假设从测试管柱至井筒水泥环外边缘的传热过程是稳态的,从井筒水泥环外边缘至地层的传热过程是非稳态的。
2.2 套管环空温度计算由于在正常测试和生产作业时,可以在清井和采油时通过水下井口控制A环空的压力,但对于B环空和C环空的压力控制比较困难。为此,现以B环空为例,建立套管环空温度计算模型,A环空和C环空与B环空类似。
某一深度h处从测试管柱传递至井筒水泥环外边缘的热量梯度为:
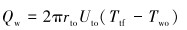
|
(1) |
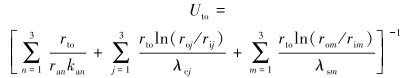
|
(2) |
式中:Qw为从测试管柱传递至井筒水泥环外边缘的热量梯度,W/m;Uto为测试管柱外壁至井筒水泥环外边缘总传热系数,W/(m2·℃);rto为测试管柱外半径,m;Ttf为测试管内流体温度,℃;Two为井筒水泥环外边缘温度,℃;ran为井筒中轴线至第n个环空外边缘距离,m;kan为第n个环空的传热系数,W/(m2·℃);roj、rij分别为第j层套管的外半径和内半径,m;λcj为第j层套管的导热系数,W/(m·℃);rom、rim分别为第m层水泥环的外半径和内半径,m;λsm为第m层水泥环的导热系数,W/(m· ℃)。
某一深度h处从井筒水泥环外边缘传递至地层的热量梯度为:
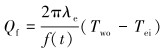
|
(3) |
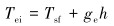
|
(4) |
式中:Qf为从井筒水泥环外边缘传递至地层的热量梯度,W/m;f(t)为无因次地层导热时间函数;Tei为地层初始温度,℃;Tsf为海底温度,℃;ge为地温梯度,大概每100 m为3 ℃;h为井筒任意位置与海底的距离,m。
根据能量守恒原理可得:
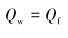
|
(5) |
于是有:
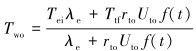
|
(6) |
由于从测试管柱至井筒水泥环外边缘的传热过程是稳态的,所以B环空内的流体温度为:
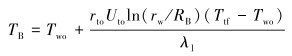
|
(7) |
式中:TB为B环空的流体温度,℃;RB为B环空的外边缘半径,m;rw为井眼半径,m;λl为环空内流体导热系数,W/(m·℃)。
上述公式中,不同时刻油管内流体温度分布Ttf的具体计算公式参考文献[8]。
2.3 套管环空压力预测模型根据前文所建的环空流体温度模型,以B环空为例进一步推导套管环空压力预测模型,A环空和C环空与B环空类似。PVT状态方程是套管环空压力预测的基础,对该方程求偏微分可得:
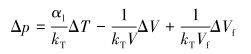
|
(8) |
式中:Δp为环空压力变化,MPa;αl为环空流体热膨胀系数,℃-1;kT为环空流体等温压缩系数,MPa-1;ΔT为环空温度变化,℃;V、ΔV分别为环空体积及其变化量,m3;Vf、ΔVf分别为环空内流体体积及其变化量,m3。
不同的流体类型,套管环空流体等温压缩系数kT和热膨胀系数αl常常不同。由于套管环空为密闭空间,环空内流体体积无变化,于是有ΔVf=0。套管环空体积变化由套管和环空流热膨胀或压缩引起,主要包括由于套管径向热膨胀、套管径向压缩、环空流体热膨胀和环空流体压缩共4部分引起的环空体积增大或减小,具体计算公式详见文献[9]。
B环空的总体积变化量可以表示为:
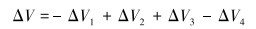
|
(9) |
式中:ΔV1、ΔV2、ΔV3、ΔV4分别表示由于套管径向热膨胀、套管径向压缩、环空流体热膨胀和环空流体压缩引起的环空体积变化,m3。
3 模型求解笔者利用牛顿下山法求解环空压力。一者是该方法考虑了环空圈闭压力是环空体积和压力耦合变化而形成的,利用迭代法更加满足其物理形成过程;二者是在保证收敛速度快的前提下,牛顿下山法可有效克服利用简单迭代法和牛顿迭代法时初值选取的问题[10],提高了工程的可操作性。
牛顿下山法计算的基本步骤如下。
(1) 通过整合式(6)和式(7),进一步化简得到环空压力的函数关系,即有:
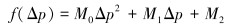
|
(10) |
式中:M0、M1和M2均为中间计算的拟合系数。
(2) 给出牛顿下山法的迭代计算公式,即有:
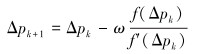
|
(11) |
(3) 对公式(11)进行数值迭代,直至满足迭代停止条件时停止计算。
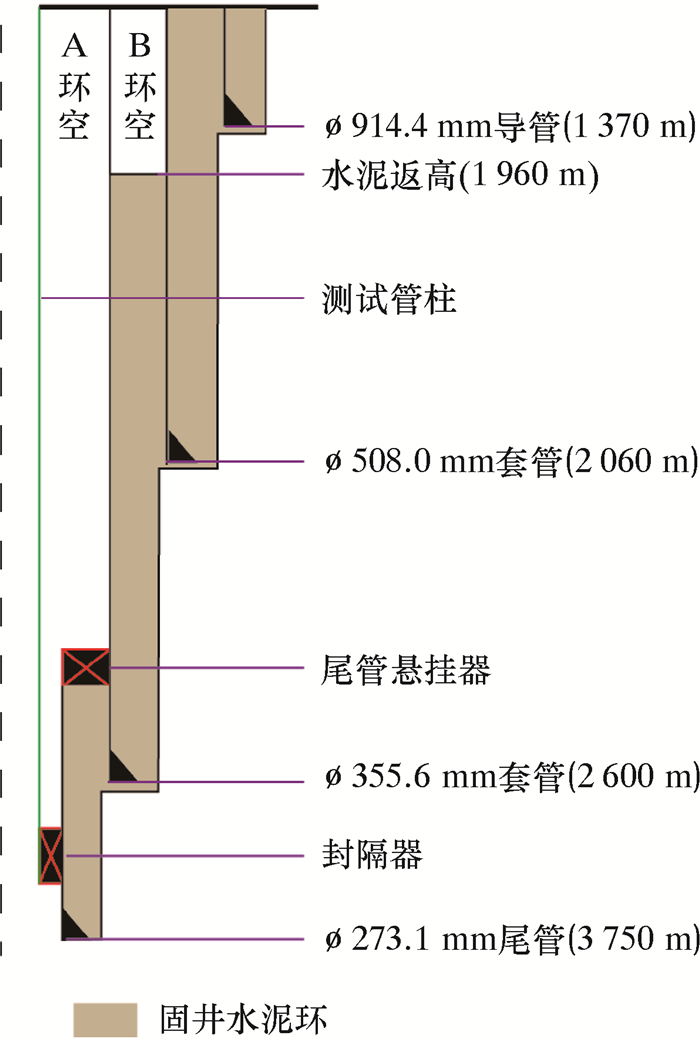
4 应用实例分析利用文献[11]中西非海域某油田7口深水井B环空的温度和压力现场监测值对文中模型进行验证。该油田典型深水井井身结构如图 2所示。
|
| 图 2 西非某深水油田典型生产井井身结构示意图 Fig.2 Wellbore configuration of a typical production well in a deepwater field in West Africa |
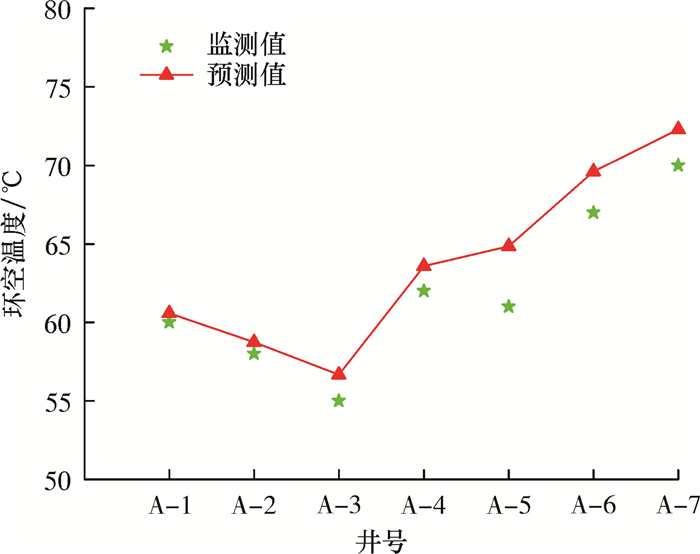
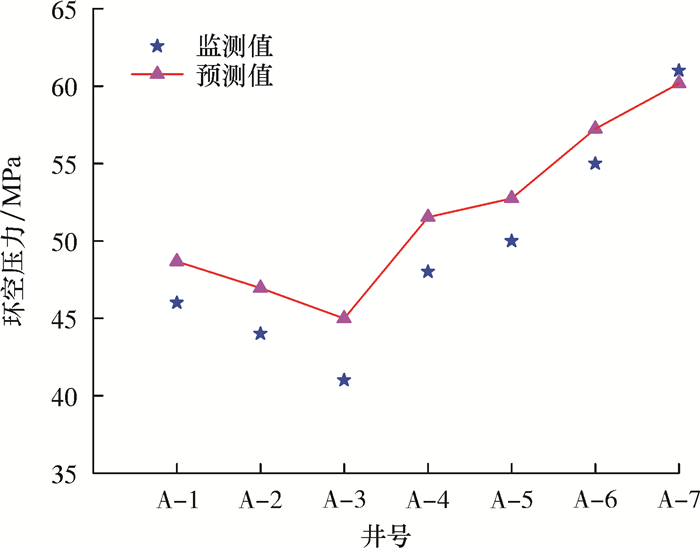
根据该油田实际地层流体物性、套管导热系数及套管尺寸等参数,利用笔者推导的套管环空温度计算公式及套管环空压力预测模型进行计算,并与现场实际监测值进行对比,结果如图 3和图 4所示。
|
| 图 3 环空温度模型预测值与监测值对比 Fig.3 Comparison of model predicted and monitored annulus temperature |
|
| 图 4 环空圈闭压力模型预测值与监测值对比 Fig.4 Comparison of model predicted and monitored annulus pressure |
由图 3和图 4可以看出,7口井的套管环空温度和压力的预测值与监测值非常接近,其最大相对误差均在10%以内,精度满足工程要求,表明笔者所建模型计算结果符合现场实际情况。
利用牛顿下山法后,计算1口井的平均时间为1.8 s,而利用简单迭代法需要2.5 s,计算速度相对加快。随着计算量的增大,牛顿下山法省时的效果将更加明显,更适合现场大量数据计算使用。
5 结论(1) 基于深水井井身结构和井筒传热过程,通过推导深水钻完井套管环空温度计算公式,并分析套管环空体积随温度和压力的变化量,建立了套管环空压力的预测模型。
(2) 与西非油田现场监测值对比结果表明,7口井的套管环空温度和压力的预测值与监测值非常接近,其最大相对误差均在10%以内,精度满足工程要求,表明笔者所建模型计算结果符合现场实际情况。
(3) 在保证收敛速度快的前提下,提出用牛顿下山法求解环空压力,有效克服了利用简单迭代法和牛顿迭代法时初值选取的问题;并且随着计算量的增大,牛顿下山法省时的效果将更明显,更适合现场大量数据计算使用。
| [1] |
周波, 杨进, 刘正礼, 等. 深水油气井筒环空注氮控压机理[J].
石油勘探与开发, 2015, 42(3): 386-389.
ZHOU B, YANG J, LIU Z L, et al. Mechanism of pressure management by injecting nitrogen in casing annulus of deepwater wells[J]. Petroleum Exploration and Development, 2015, 42(3): 386-389. |
| [2] |
胡伟杰, 王建龙, 张卫东. 深水钻井密闭环空圈闭压力预测及释放技术[J].
中外能源, 2012, 17(8): 41-45.
HU W J, WANG J L, ZHANG W D. Confined annular trap pressure prediction and release technology for deep water drilling[J]. Sino-global Energy, 2012, 17(8): 41-45. |
| [3] | PATTILLO P D, COCALES B W, MOREY S C. Analysis of an annularpressure buildup failure during drilling ahead[J]. SPE Drilling & Completion, 2006, 21(4): 242-247. |
| [4] | OUDEMAN P, KEREM M. Transient behavior of annular pressure build-upin HP/HT wells[R]. SPE 88735-PA, 2006. |
| [5] | RICHARD F V J, PAYNE M, FAUL R, et al. Practical and successful prevention of annular pressure buildup on the Marlin project[J]. SPE Drilling & Completion, 2003, 18(3): 228-234. |
| [6] | HASANA R, IZGEC B, KABIR C S. Ensuring sustained production by managing annular-pressure buildup[R]. SPE 121754-MS, 2009. |
| [7] | RAMEY H J. Wellbore heat transmission[J]. Journal of Petroleum Technology, 1962, 14(4): 427-435. DOI: 10.2118/96-PA |
| [8] |
张波, 管志川, 张琦. 深水油气井开采过程环空压力预测与分析[J].
石油学报, 2015, 36(8): 1012-1017.
ZHANG B, GUAN Z C, ZHANG Q. Prediction and analysis on annular pressure of deepwater well in the production stage[J]. Acta Petrolei Sinica, 2015, 36(8): 1012-1017. |
| [9] |
高宝奎. 高温引起的套管附加载荷实用计算模型[J].
石油钻采工艺, 2002, 24(1): 8-11.
GAO B K. Practical model for calculating the additional load on casing by high temperature[J]. Oil Drilling & Production Technology, 2002, 24(1): 8-11. DOI: 10.3969/j.issn.1000-7393.2002.01.003 |
| [10] |
张明.
应用数值分析[M]. 北京: 石油工业出版社, 2012.
ZHANG M. Applied numerical analysis[M]. Beijing: Petroleum Industry Press, 2012. |
| [11] |
杨进, 唐海雄, 刘正礼, 等. 深水油气井套管环空压力预测模型[J].
石油勘探与开发, 2013, 40(5): 616-619.
YANG J, TANG H X, LIU Z L, et al. Prediction model of casing annulus pressure for deepwater well drilling and completion operation[J]. Petroleum Exploration and Development, 2013, 40(5): 616-619. |


