2. 东北石油大学计算机与信息技术学院;
3. 东北石油大学石油工程学院
2. School of Computer and Information Technology, Northeast Petroleum University;
3. School of Petroleum Engineering, Northeast Petroleum University
0 引言
随着自然科学的发展,数字岩心建模模拟已经成为地质岩石研究的重要方法之一[1]。数字岩心始于20世纪60年代,随着计算与仪器设备的发展,Micro-CT和扫描电子显微镜等扫描设备的出现,简略的岩心模型已发展为可展示真实孔隙-骨架结构的精确岩心模型[2]。构建三维数字岩心最初的方法为序列成像法。科研人员研制了CT机并应用于数字岩心的研究[3-10]。序列成像法、CT扫描成像法和聚焦扫描成像法均利用不同的实验仪器对岩石样品直接成像构建数字岩心;而高斯法、模拟退火法和过程模拟法均利用岩心连续的微观二维图像,通过数学建模方法构建三维数字岩心[11-12]。
通过比较发现,CT扫描成像法是目前建立数字岩心的最佳技术[13]。该技术利用分辨率极高的微观成像设备直接扫描岩心,建立其数字图像,这将大幅提高数字图像重新构建的精确度且方便易行[14]。为此,笔者应用该方法建立数字岩心,重点研究X射线CT扫描法,阐述了MC算法的基本原理,并通过该方法建立了2块砂岩样品的数字岩心。
1 Micro-CT成像 1.1 X射线CT扫描设备CT成像技术具有无损伤透视的特点,近年来,其应用研究一直被视为热点。CT技术的主要功能是研究液体的渗透性与物理状态,研究岩石的变形,分析断层及断裂等[15]。一般情况下,CT可以用来观察岩石内部无法用肉眼观测到的孔隙结构变化过程,是岩石地质工程方面的一个实用、有力且无损伤的观察分析方法[16]。
常用的X射线CT扫描设备主要包括医疗CT、Micro-CT和Nano-CT[17]。医疗CT的分辨率较低,通常为0.5 mm,可用于对非均质性全岩心的粗扫;分辨率最高的是Micro-CT,可达0.5 μm,可用于非致密岩石样品的精扫,可以从微米尺度观测岩心内部拓扑结构,扫描时间较短,扫描视野范围比Nano-CT更大,因此在岩石数值模拟研究中更多采用Micro-CT。我国学者在岩石CT扫描成像领域的研究始于20世纪90年代初期,但后期进展较迅速。利用CT对岩心试样的内部孔隙结构进行研究,具有以下优势:
(1) 非破坏性。在研究过程中岩心样品长期保持不受干扰状态。
(2) 持续性。利用CT技术可以十分简单地持续观察岩心的内部孔隙结构演化。
(3) CT成像技术既可以显示岩心试样的三维特征,也可显示任意横截面的二维图像。
(4) 根据岩心试样的固定化学物理性质,用CT图像技术可以分析岩心的其他性质。
1.2 Micro-CT的工作原理X射线CT是通过无数平行射线扫描被测样品时获得的吸取数据来重建其任意断层表面影像的设备[18],如图 1所示,主要由X射线源、载物平台、CCD探测器和闪烁计数器等构成。当一束平行射线穿过岩心试样的一个断层时,射线所涉及路径的总衰减指数与体素衰减指数密切相关,呈线积分形式,探测器将平行射线强弱转化为电信号,之后通过计算机进行数字化处理。
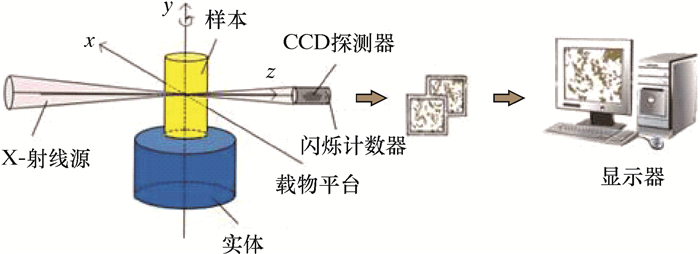
|
| 图 1 Micro-CT扫描示意图 Fig.1 Schematic diagram of Micro-CT scanning |
应用CT扫描成像技术可以获得岩石的三维立体灰度影像,影像里不同的灰度值表示不同的岩石。采用一定算法可以把三维灰度影像分成岩心骨架和岩心孔隙2部分,用对应数值表示,这样就得到了数字化的岩石,也就是数字岩心。经CT扫描成像技术得到的影像是对岩心密度的描述[19]。
2 MC算法建立数字岩心 2.1 MC算法建立数字岩心的原理MC的原理是将一组二维CT影像看成一个立体数据库,选取连续2层相接的8个点组成大小相等的三维图形,称为体素[20],角点为体素的任何一个顶点。MC算法是一种将某一实物的一系列二维断层图像通过处理之后,重建出该实物三维实体的算法;其原理为在空间中构建体元(cube),寻找到接触等值面,也就是实物的体表面体元,然后在体元内部使用三角形截面来拟合等值面,最后遍历体元得到用三角形截面来表达实体。
2.2 具体实施步骤MC算法的输入假设为一系列二维断层图像、输出则为所有三角面片。
2.2.1 在空间中构建体元立方体体元如图 2所示,取2张断层图像,构成一层。取上下相邻的8个像素点作为体元的上顶面和下底面,每一张图片都由若干个像素点构成,每个像素点都有描述其亮度的灰度值,高度应该是断层的高,于是就得到了一个体元。

|
| 图 2 立方体体元 Fig.2 The cube element |
找边界体元是用体元的所有角点值依次与阈值相比较,一个体元内存在一个角点值等于或大于阈值的同时也存在一个角点值小于阈值,那么该体元就是边界体元[21]。
将边界体元中的8个角点值分别与阈值比较,如果某个角点值大于等于阈值,则说明该角点在目标实体内,将该角点标记为1;如果某个角点值小于阈值,则说明该角点在目标实体外,将该角点标记为0。遍历边界体元的8个角点,就能得到各个角点是否在实体内的分布情况。据此可知,如果边界体元一条边两角的角点标记值不一样,也就是一个角点在实体外,一个角点在实体内,那么等值面必经过这一条边。根据这个结论,从角点的标记情况可以得出等值面与边界体元的哪些边相交,从而可以得出三角形截面的分布情况,也即用来拟合的三角面片的顶点分布在哪些边上是可知的,顶点具体的位置还要进一步计算。一个体元共有8个角点,任何一个角点的标记情况只有0和1,所以8个角点的标记情况共有28=256种,即相交情况有256种。体元标记分类如图 3所示,每一种相交情况对应一个三角形截面的分布状况。由于每个体素的顶点均具有不变性和对称性,以上的256种情况可总结为以下15种状态[22]。
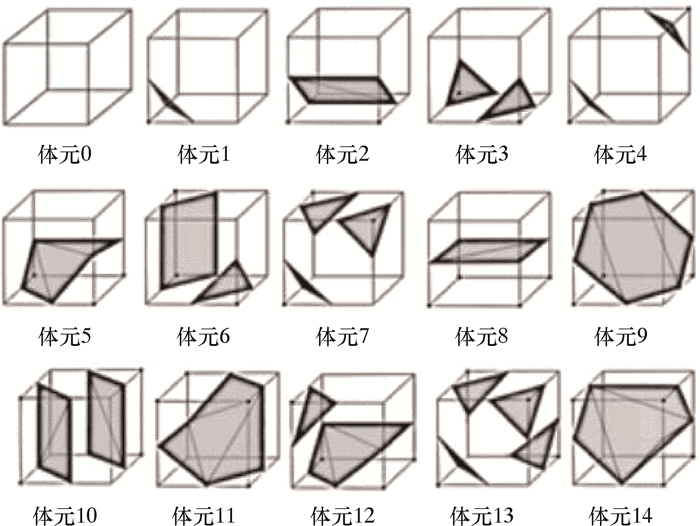
|
| 图 3 体元标记分类 Fig.3 Mark and classification of the elements |
2.2.2 计算三角形截面的顶点坐标和法向量
得知了三角形截面3个顶点的位置分布,就需要具体确定三角形截面3个顶点在体元边上的位置,也就是顶点坐标。已知顶点在边上,边的2个角点值一个大于阈值,一个小于阈值。MC算法假设值呈线性变化,因此通过计算可以得到每一个顶点的具体位置。
2.2.2.1 顶点坐标如果交点所在的棱边在X轴上,则交点的坐标为:
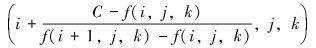
|
其中,f(i,j,k)指(i,j,k)坐标下的灰度值,表示阈值。交点在Y、Z轴上的坐标分别为:
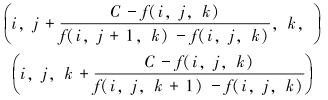
|
用中心差分公式计算体元各顶点法向量为:
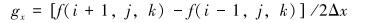
|
(1) |
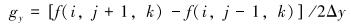
|
(2) |
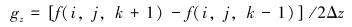
|
(3) |
式中:Δx、Δy、Δz分别代表体元3个方向上的间距,通常Δx=Δy,Δz比较大,gx、gy、gz分别代表坐标(x,y,z)点3个方向上的梯度值,法向量就是gx、gy、gz。
如果交点所在的棱边在X轴上,则交点的法向量为:
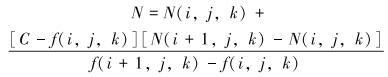
|
(4) |
若交点所在的棱边在Y、Z轴上,则交点的法向量分别为:
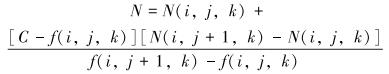
|
(5) |
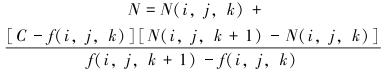
|
(6) |
式中:N为交点法向量,N(i,j,k)为坐标(i,j,k)的向量值,C为阈值。
以上4步都是在一个体元内进行的操作,因此在一层中从左至右、从上到下逐个遍历体元,然后逐层遍历体元,就能得到用三角形截面拟合的实体。
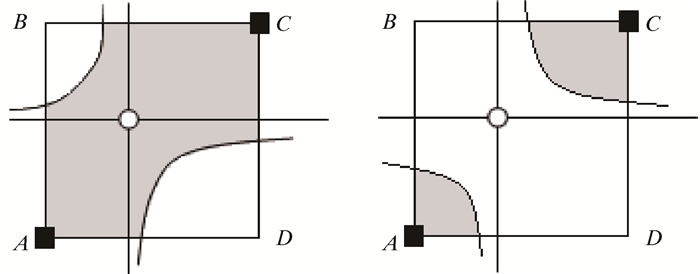
2.3 MC算法的二义性问题及其改进方案 2.3.1 MC算法体元二义性问题 2.3.1.1 面二义性当立方体表面的一组对角顶点为正,相反另一组对角顶点为负,这时就产生了面二义性,如图 4所示。
|
| 图 4 面二义性 Fig.4 The plane ambiguity |
2.3.1.2 体二义性
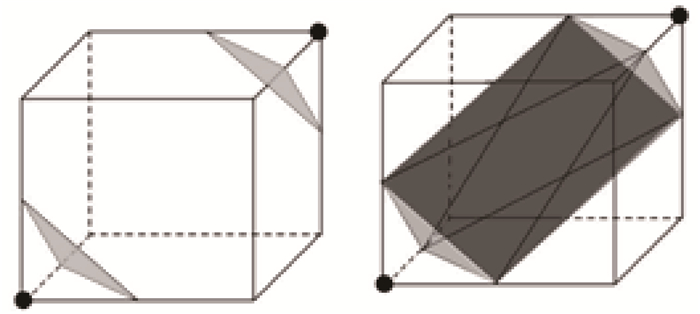
交点不同的相交方式存在于体素外部,同样体素内部也有相似情况,例如体素的2个体对角顶点在等值面中时,在等值面外部是其余顶点,如图 5所示。
|
| 图 5 体二义性 Fig.5 The body ambiguity |
2.3.1.3 二义性问题解决方法
如果遍历体元过程中出现面二义性或者体二义性,就将该体元拆分成形状大小完全相同的8个小体元,已知8个角点的值可以通过线性插补的方式求出其中点的值,同样求出中心点的值,像MC算法里面遍历体元一样对该8个小体元进行遍历,抽取等值面。如果该8个小体元中出现面二义性或者体二义性,则重复该步骤。通过查找文献可知,该过程一般一次就能解决二义性问题,2次的记录约为3%,3次及3次以上很罕见。
2.3.2 抽取等值面的改进方案 2.3.2.1 传统MC算法等值面抽取方法通过比较8个角点值与阈值的大小,可得8个角点的正负情况,正负情况就是角点在等值面内还是在等值面外。根据8个角点分布情况可以得出等值面的分布情况,MC算法通过用三角形截面拟合等值面,从而达到三维重建的目的。MC算法建立了256种三角形截面分布情况查找表。在遍历体元过程中可以得知体元的正负情况,据此从查找表中找三角形截面分布情况。利用角点值以及线性插补的原理求出三角形截面的顶点位置。
2.3.2.2 改进MC算法等值面抽取方法因为二义性问题已经解决,所以每一个体元面上都只有一条等值线。所有等值线必定首尾相连,即任何一个边界体元都可以得到一个空间多边形。任何一个空间多边形都可以由三角形截面填满,因此可以通过简单的算法实现空间多边形向三角形截面的转变。任何空间多边形的顶点都可以通过线性插补的方式求出来。用这种等值面抽取方法可以不建立索查表而得到三角形截面的分布状况。因为只有边界体元更加细分,所以该算法延长的运算时间和内存空间可以接受,而且重建得更加精细。
3 三维数字岩心重建实例MC重建过程如图 6所示。具体步骤如下:
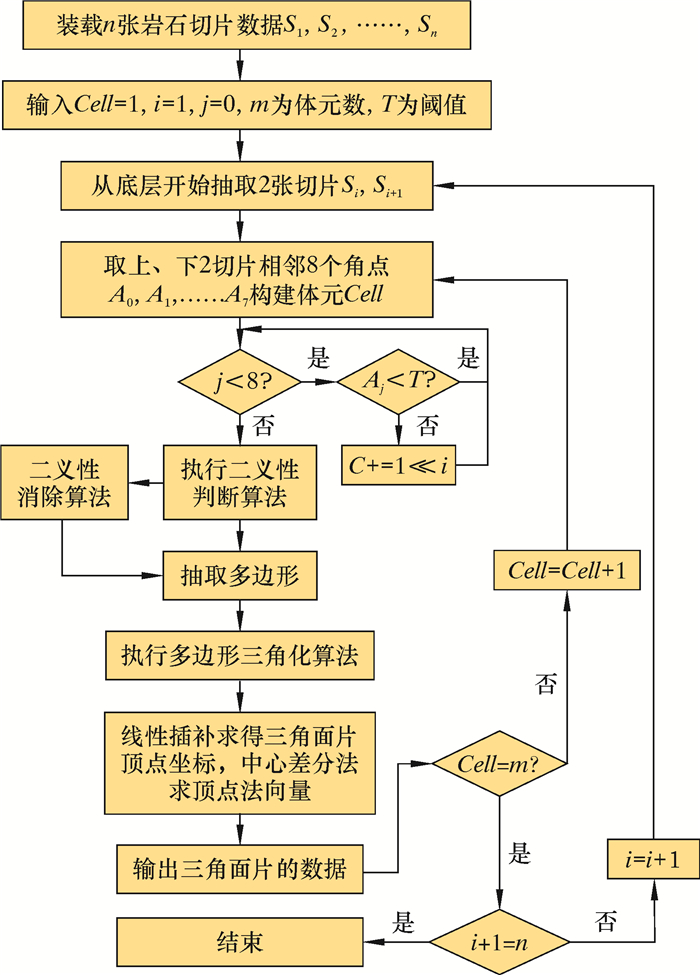
|
| 图 6 MC算法建立数字岩心的程序框图 Fig.6 Block diagram of the digital core establishment using MC algorithm |
(1) 装载n张切片数据S1, S2,……,Sn,从底层开始抽取2张切片Si,Si+1构成一层,其中i从0开始。
(2) 从2张切片上抽取相接的4个角点构成立方体元,从而得体元的所有角点A0, A1,……,A7。将体元标记为Cell(Cell取值范围为1~m)。
(3) 在一个体元中,从第1个角点开始比较Aj(j取值范围为0~7)角点值与阈值的大小。如果角点值大于阈值,则给变量C(C的初始值为0)加上1≪j(1向左移j位),并且j的值加1,如果角点值小于阈值,则变量C不变,且j的值加1。重复该过程直到j等于8。
(4) 按照获得的C值执行二义性判断算法,如果该体元存在二义性,则执行其去除算法,否则继续下一步。
(5) 依次执行多边形等值面抽取与多边形三角化算法,然后通过线性插补的方式求得三角面片的顶点坐标,通过中心差分的方式求得三角形截面角点的法向量,最后输出获得三角形截面的数据。
(6) 如果Cell值不等于体元总数m,则Cell值加1并且继续遍历体元;如果Cell值等于体元总数m,则判断切片数是否重建完毕,即i+1是否等于总切片数n,如果不等于n,则i值加1,继续抽取下一张切片与原来的后一张切片构成一层,重复执行上述遍历体元的操作;如果等于n,则切片重建完毕,算法结束。
用CT岩心二维图像进行三维重建需采用Matlab来实现。基于MC算法,通过Matlab建立数字岩心的具体过程见图 7。根据以上重建步骤,通过MC算法分别对岩心二维CT图像进行数字岩心三维模型建立,结果如图 8所示。
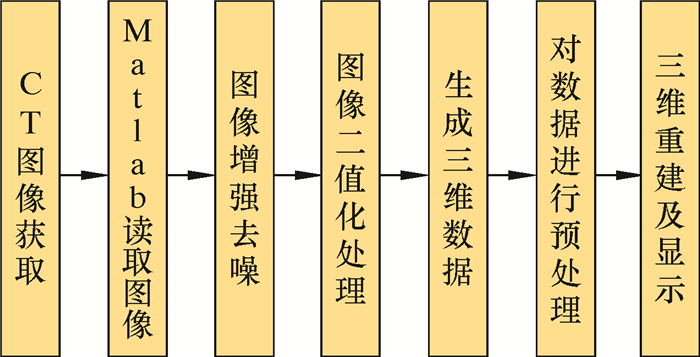
|
| 图 7 Matlab建立数字岩心的过程 Fig.7 Process of building a digital core using Matlab |

|
| 图 8 三维数字岩心重建后实例图 Fig.8 Example map of 3D digital core reconstruction |
4 结束语
三维岩心可视图像能更加直观、真实和准确地反映岩石在空间的分布情况,从而验证了构建数字岩心的重要性。MC算法三维重建时,不用建立查找表便可得到三角形截面的分布情况。通过多次试验发现此方案在保持时间优势的基础上,用改进算法所重建的孔隙分布与经典MC算法相比,有相当的优势且更加精细。因此,结合Micro-CT图像和Marching Cubes算法利用岩心切片重新构建了三维数字岩心,实现了岩心微观孔隙结构的可视化。三维数字岩心重建试验结果表明:该方法能更好地对岩石切片进行重建,且耗时较少、精度更高。
| [1] |
陶果, 岳文正, 谢然红, 等. 岩石物理的理论模拟和数值实验新方法[J].
地球物理学进展, 2005, 20(1): 4-11.
TAO G, YUE W Z, XIE R H, et al. A new method for theoretical modeling and numerical experiments on petrophysical studies[J]. Progress in Geophysics, 2005, 20(1): 4-11. DOI: 10.3969/j.issn.1004-2903.2005.01.002 |
| [2] |
姚军, 赵秀才, 衣艳静, 等. 数字岩心技术现状及展望[J].
油气地质与采收率, 2005, 12(6): 52-54.
YAO J, ZHAO X C, YI Y J, et al. The current situation and prospect on digital core technology[J]. Petroleum Geology and Recovery Efficiency, 2005, 12(6): 52-54. |
| [3] |
马淑芳, 韩大匡, 甘利灯, 等. 地震岩石物理模型综述[J].
地球物理学进展, 2010, 25(2): 460-471.
MA S F, HAN D K, GAN L D, et al. A review of seismic rock physics models[J]. Progress in Geophysics, 2010, 25(2): 460-471. |
| [4] | DVORKIN J, FANG Q, DERZHI N. Etudes in computational rock physics:Alterations and benchmarking[J]. Geophysics, 2012, 77(3): 45-52. |
| [5] |
刘善琪, 李永兵, 田会全, 等. 含湿孔隙岩石有效热导率的数值分析[J].
地球物理学报, 2012, 55(12): 4239-4248.
LIU S Q, LI Y B, TIAN H Q, et al. Numerical simulation on thermal conductivity of wet porous rock[J]. Chinese Journal of Geophysics, 2012, 55(12): 4239-4248. DOI: 10.6038/j.issn.0001-5733.2012.12.035 |
| [6] | DVORKIN J, DERZHI N, DIAZ E, et al. Relevance of computational rock physics[J]. Geophysics, 2011, 76(5): 141-153. DOI: 10.1190/geo2010-0352.1 |
| [7] | LYMBEROPOULOS D P, PAYATAKES A C. Derivation of topological, geometrical, and correlational properties of porous media from pore-chart analysis of serial section data[J]. Journal of Colloid and Interface Science, 1992, 150(1): 61-80. DOI: 10.1016/0021-9797(92)90268-Q |
| [8] | VOGEL H J, ROTH K. Quantitative morphology and network representation of soil pore structure[J]. Advances in Water Resources, 2001, 24(3/4): 233-242. |
| [9] | TOMUTSA L, RADMILOVIC V. Focused ion beam assisted three-dimensional rock imaging at submicron scale[C]//Proceedings of International Symposium of the Society of Core Analysts. California: Ernest Orlando Lawrence Berkeley National Laboratory, 2003. |
| [10] | TOMUTSA L, SILIN D. Nanoscale pore imaging and pore scale fluid flow modeling in chalk[C]//Proceedings of 25th Annual Workshop and Symposium Collaborative Project on Enhanced Oil Recovery, Stavanger. Berkeley, California: Ernest Orlando Lawrence Berkeley National Laboratory, 2004. |
| [11] |
蔡涵鹏, 贺振华, 唐湘蓉, 等. 碳酸盐岩孔隙结构影响分析和等效孔隙结构参数计算[J].
石油物探, 2013, 52(6): 566-572.
CAI H P, HE Z H, TANC X R, et al. Influence analysis of carbonate pore structure and calculation of equivalent pore structure parameters[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 566-572. |
| [12] |
曾筝, 董芳华. 利用MATLAB实现CT断层图像的三维重建[J].
CT理论与应用研究, 2004, 13(2): 24-29.
ZENG Z, DONG F H. Three dimensions reconstruction of CT image by MATLAB[J]. CT Theory and Applications, 2004, 13(2): 24-29. |
| [13] |
杨凤英, 印兴耀, 刘博. 可变干岩石骨架等效模型研究[J].
石油物探, 2014, 53(3): 280-286.
YANG F Y, YIN X Y, LIU B. The research of variable dry rock matrix equivalent model[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 280-286. |
| [14] | HAZLETT R D. Statistical characterization and stochastic modeling of pore networks in relation to fluid flow[J]. Mathematical Geology, 1997, 29(6): 801-822. DOI: 10.1007/BF02768903 |
| [15] | MANWART C, TORQUATO S, HILFER R. Stochastic reconstruction of sandstones[J]. Physical Review E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2000, 62: 893-899. |
| [16] | NELSON P H. Permeability-porosity relationships in sedimentary rocks[J]. Log Analyst, 1994, 35(3): 38-62. |
| [17] |
李兵, 凌其聪, 鲍征宇, 等. 用数字化图像分析法确定岩石物性[J].
新疆石油地质, 2008, 29(2): 253-255.
LI B, LING Q C, BAO Z Y, et al. Application of digital image processing to determination of petrophysical property[J]. Xinjiang Petroleum Geology, 2008, 29(2): 253-255. |
| [18] | MOWERS T T, BUDD D A. Quantification of porosity and permeability reduction due to calcite cementation using computer-assisted petrographic image analysis techniques[J]. AAPG Bulletin, 1996, 80(3): 309-321. |
| [19] |
谢月芳, 张纪. 岩石物理模型在横波速度估算中的应用[J].
石油物探, 2012, 51(1): 65-70.
XIE Y F, ZHANG J. Application of rock physical model in S-wave velocity estimation[J]. Geophysical Prospecting for Petroleum, 2012, 51(1): 65-70. |
| [20] | LEWITT R M. Reconstruction algorithms:Transform methods[J]. Proceedings of the IEEE, 1983, 71(3): 390-408. DOI: 10.1109/PROC.1983.12597 |
| [21] | COENEN J, TCHOUPAROVA E, JING X. Measurement parameters and resolution aspects of micro X-ray tomography for advanced core analysis[C]//Proceedings of International Symposium. Abu, Dhabi: Core Analysts, 2004. |
| [22] |
戴贤忠, 李小孟, 王家新, 等. CT在油气藏储量计算参数测定中的应用[J].
石油学报, 1993, 14(4): 60-68.
DAI X Z, LI X M, WANG J X, et al. Application of computer tomography to the determination of porosity and oil saturation in a core sample[J]. Acta Petrolei Sinica, 1993, 14(4): 60-68. |




