2. 中国石油集团工程技术研究院有限公司;
3. 中国石油勘探开发研究院;
4. 中国石油集团渤海钻探工程有限公司第五钻井工程分公司
2. CNPC Engineering Technology R & D Company Limited;
3. Research Institute of Petroleum Exploration & Development, CNPC;
4. NO.5 Drilling Engineering Branch of BHDC CNPC
0 引言
随着有水气藏开发程度的不断增大,地层压力和产气量逐渐减小,导致气体的携液能力下降,边底水不断入侵,井底积液量逐渐增加,从而造成气井产量大幅度降低,甚至停产,极大地增加气井的开采成本,影响经济效益[1-2]。因此,需要采用优选管柱(连续管)、泡排、气举、有杆泵、电潜泵及射流泵等排水采气工艺,来维持气井的持续稳定开采。目前,连续管排水采气工艺在国内外各大气田(Saudi Arabia、Gomez、川西、塔里木、大牛地和苏里格等气田)进行了广泛的试验与应用,获得较好的排水采气效果,为改善有水气藏的开发效果提供了技术支持[3-11]。随着气田开发的逐渐深入,低产气井将不断增多,该技术的应用前景广阔。
连续管排水采气工艺是通过在生产管柱中安装优选的小直径连续管来减小流动面积,面积减小会导致管柱内气体流速的增大,当管柱底部气体流速大于临界携液流速时,气井井底不产生积液,生产得以恢复;而流动面积减小将导致管柱内压降增大,满足稳定携液的同时,亦需要井口压力大于输压以确保能将天然气输给用户或采气管网[2]。连续管排水采气工艺设计的理论基础是连续携液机理和连续管气液两相流压降模型。目前对连续携液机理的研究已日趋成熟,主要分为2类:一类是液滴理论模型,认为液相是以液滴形式被携带和运移,若井筒内最大直径液滴不发生滑脱,则井底不会出现积液现象;另一类是液膜理论模型,认为液相是以液膜形式被携带出井筒。而对连续管气液两相流压降模型的研究涉及较少。目前常用的两相流压降模型主要有9种,分别是Ansari模型[12]、Beggs-Brills模型[13]、Duns-Ros模型[14]、Govier-Aziz-Fogarasi模型[15]、Gray模型[16]、Hagedorn-Brown模型[17]、Mukherjee-Brill模型[18]、No-Slip模型[19]和Orkiszewski模型[20]。常规管柱气液两相流压降模型的评价结果表明,Hagedorn-Brown模型与Beggs-Brills模型计算的误差最小[21]。但由于连续管管径较小,在相同流量条件下,不同气液比的气液混合物流速高于常规管柱,且流型与滑脱损失程度不同于常规管柱,若采用常规管柱气液两相流压降模型进行相应计算,势必会导致连续管气液两相流压降计算结果有一定的误差,甚至错误。因此,有必要依据连续管排水采气井实测数据对常用两相流压降模型进行评价和优选,利用9种常用模型计算所得的井底压力与实测数据进行对比,并分析不同气液比时各模型计算的相对误差分布,确定其适用范围与精度,从而为提高连续管排水采气工艺设计与排液效果分析水平提供相应的理论支撑。
1 模型的评价笔者利用1963年O.D.GAITHER[22]和1988年C.M.RENDEIRO[23]公开发表的121组连续管排水采气井实测数据进行两相流压降模型评价。其中,Gaither文献中包括25.4 mm(1 in)和38.1 mm(1.5 in)2种管径的连续管,而Rendeiro文献中的连续管管径为50.8 mm(2 in)。
1.1 利用O.D.GAITHER文献实测数据整理了O.D.GAITHER文献中57井次的实测数据(Ø25.4 mm连续管),对9种气液两相管流压降模型进行评价。气井的基本情况为:井型为直井,井深305 m,气流量0.27×104~2.95×104 m3/d,气液比79~1 069 m3/m3,实测井口压力0.43~3.56 MPa,实测井底压力1.61~5.48 MPa,井口温度22.09~38.76 ℃,井底温度31.24~47.91 ℃。
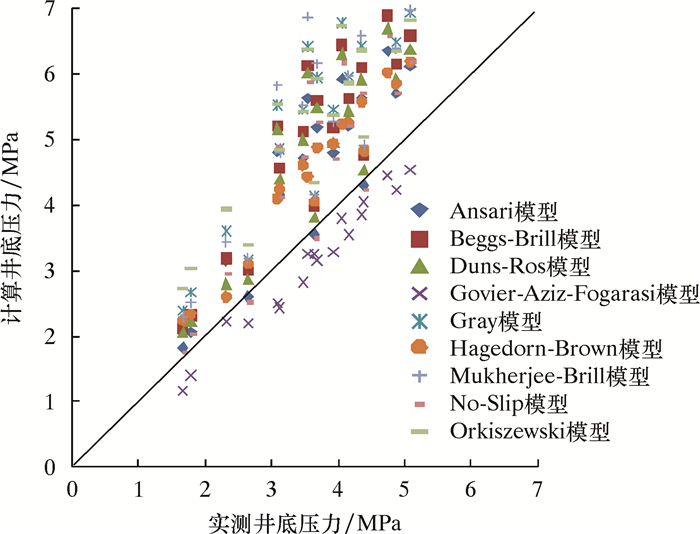
9种计算模型井底压力计算值和实测值对比结果如图 1所示。从图可发现:Hagedorn-Brown模型的计算结果和实测井底压力比较接近;Ansari模型、Beggs-Brill模型、Duns-Ros模型、Gray模型、Mukherjee-Brill模型、No-Slip模型和Orkiszewski模型的计算结果与实测井底压力相比,整体偏大;而Govier-Aziz-Fogarasi模型的计算结果与实测井底压力相比,整体偏小。

|
| 图 1 9种模型的井底压力计算值与实测值对比 Fig.1 Comparison of calculation results and measured values of bottom hole pressure using the 9 models (Ø25.4 mm连续管) (Ø25.4 mm coiled tubing) |
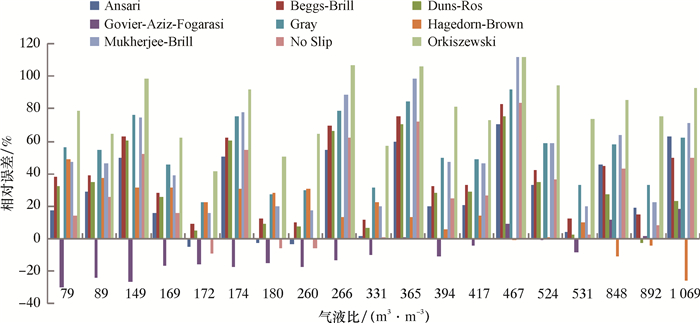
不同气液比条件下9种计算模型的相对误差见图 2。从图可明显看出,在79~1 069 m3/m3低气液比条件下,除了Govier-Aziz-Fogarasi模型和Hagedorn-Brown模型以外,其他7种计算模型的相对误差均较大;且气液比在331 m3/m3时,Govier-Aziz-Fogarasi模型和Hagedorn-Brown模型的相对误差变化较为明显。
|
| 图 2 不同气液比时9种模型的相对误差分布 Fig.2 Relative error of the 9 models under different gas-liquid ratios (Ø25.4 mm连续管) (Ø25.4 mm coiled tubing) |
经过分析整理,得到不同气液比条件下精度较高的计算模型:气液比在79~1 069 m3/m3范围内,Govier-Aziz-Fogarasi模型的平均相对误差为8.84%,精度最高,其次是Hagedorn-Brown模型,平均相对误差为15.68%,其余计算模型的平均相对误差均高于28.49%;气液比小于331 m3/m3时,Govier-Aziz-Fogarasi模型的平均相对误差为19.50%,计算精度最高,其次是Hagedorn-Brown模型,平均相对误差为30.48%;气液比大于331 m3/m3时,Hagedorn-Brown模型的平均相对误差为2.36%,精度最高,其次是Govier-Aziz-Fogarasi模型,平均相对误差为2.83%;随着气液比的不断增大,2个计算模型的平均相对误差显著下降。
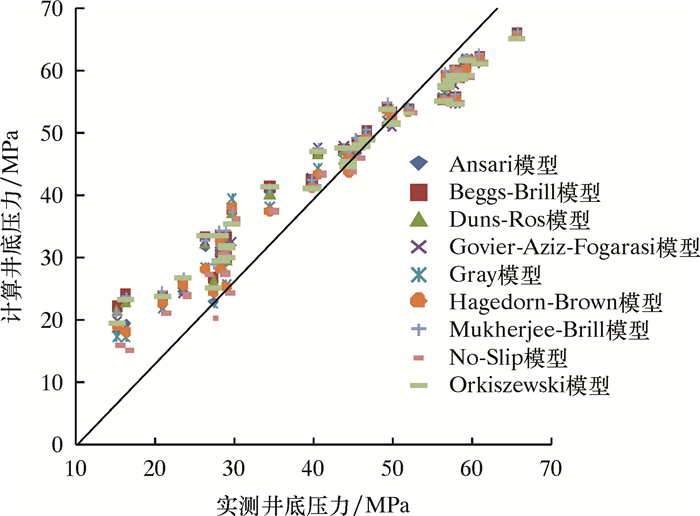
整理了O.D.GAITHER文献中18井次的实测数据(Ø38.1 mm连续管),对9种气液两相流压降模型进行评价。气井的基本情况为:井型为直井,井深305 m,气流量0.54×104~2.51×104 m3/d,气液比89~475 m3/m3,实测井口压力0.43~3.56 MPa,实测井底压力1.61~5.48 MPa,井口温度24.87~33.21 ℃,井底温度34.02~42.35 ℃。9种计算模型井底压力计算值和实测值对比结果如图 3所示。
|
| 图 3 9种模型的井底压力计算值与实测值对比 Fig.3 Comparison of calculation results and measured values of bottom hole pressure using the 9 models (Ø38.1 mm连续管) (Ø38.1 mm coiled tubing) |
从图 3可发现:Ansari模型、Beggs-Brills模型、Duns-Ros模型、Gray模型、Hagedorn-Brown模型、Mukherjee-Brill模型、No-Slip模型和Orkiszewski模型的计算结果偏大;而Govier-Aziz-Fogarasi模型的计算结果与实测井底压力相比,整体偏小。
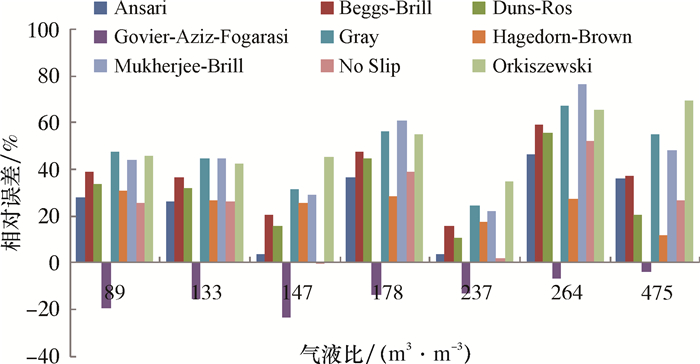
不同气液比条件下9种计算模型的相对误差见图 4。从图可明显看出,在89~475 m3/m3低气液比条件下,除了Govier-Aziz-Fogarasi模型以外,其他8种计算模型的相对误差均较大。经过分析整理,得到精度较高的计算模型:Govier-Aziz-Fogarasi模型的平均相对误差为13.76%,精度最高,其余计算模型的平均相对误差均高于24.07%。
|
| 图 4 不同气液比时9种模型的相对误差分布 Fig.4 Relative error of the 9 models under different gas-liquid ratios (Ø38.1 mm连续管) (Ø38.1 mm coiled tubing) |
1.2 利用C.M.RENDEIRO文献测试数据
整理了C.M.RENDEIRO文献中2个气田46井次的测试数据(Ø50.8 mm连续管),对9种气液两相流压降模型进行评价。Railroad commission气田连续管排水采气井的基本情况为:井型为直井,井深2 206~4 105 m,气流量1.50×104~20.32×104 m3/d,气液比151~14 489 m3/m3,实测井口压力7.76~50.40 MPa,实测井底压力15.12~65.57 MPa,井口温度19.44~86.67 ℃,井底温度103.89~146.11 ℃。Govier and Fogarasi气田连续管排水采气井的基本情况为:井型为直井,井深1 121~2 638 m,气流量2.61×104~30.02×104 m3/d,气液比695~11 990 m3/m3,实测井口压力3.00~9.74 MPa,实测井底压力4.40~22.27 MPa,井口温度7.78~50.00 ℃,井底温度为35.56~86.11 ℃。
利用Railroad commission气田33组连续管排水采气井生产实测数据,对比9种模型计算的井底压力和实测井底压力,结果如图 5所示。从图可以发现:Govier-Aziz-Fogarasi模型、Hagedorn-Brown模型、Ansari模型、Beggs-Brill模型、Duns-Ros模型、Gray模型、No-Slip模型和Orkiszewski模型的计算结果和实测井底压力均比较接近;Mukherjee-Brill模型的计算结果与实测井底压力相比,整体偏大。
|
| 图 5 9种模型的井底压力计算值与实测值对比 Fig.5 Comparison of calculation results and measured values of bottom hole pressure using the 9 models (Railroad commission气田) (Railroad commission gas field) |
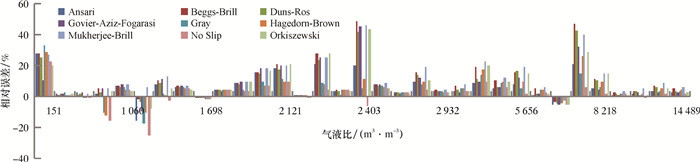
不同气液比条件下,9种计算模型的相对误差分布如图 6所示。
|
| 图 6 不同气液比时9种模型的相对误差分布 Fig.6 Relative error of the 9 models under different gas-liquid ratios (Railroad commission气田) (Railroad commission gas field) |
从图 6可看出,气液比在1 283、2 403和7 997 m3/m3附近相对误差变化较为明显。经过分析整理,得到不同气液比条件下精度较高的计算模型:气液比在151~14 489 m3/m3范围内,No-Slip模型的平均相对误差为1.57%,精度最高,其次是Gray模型,平均相对误差为4.54%;当气液比小于1 283 m3/m3时,所有计算模型的平均相对误差均低于10%,其中No-Slip模型的平均相对误差最小,为1.97%;气液比为1 283~2 403 m3/m3时,所有计算模型的平均相对误差均低于10%,其中No-Slip模型的平均相对误差最小,为0.58%;气液比为2 403~7 997 m3/m3时,除Beggs-Brill和Mukherjee-Brill模型外,其余计算模型平均相对误差均低于10%,其中No-Slip模型的平均相对误差最小,为2.26%;当气液比大于7 997 m3/m3时,除Mukherjee-Brill模型外,其余计算模型平均相对误差均低于10%,其中No-Slip模型的平均相对误差最小,为1.80%。
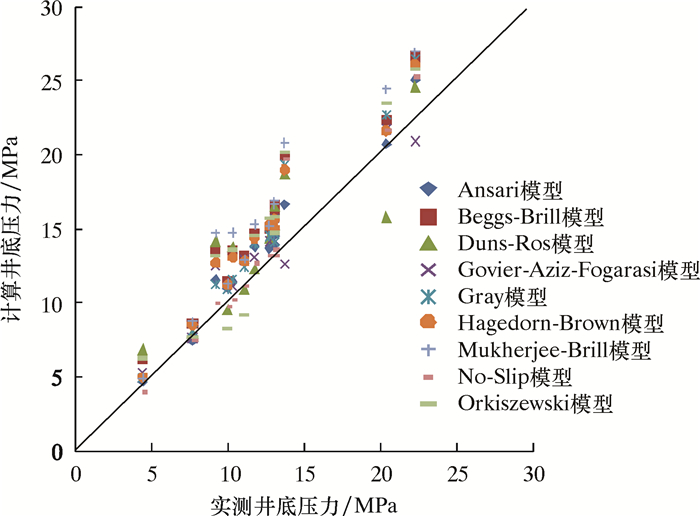
利用Govier and Fogarasi气田13组连续管排水采气井生产实测数据,对比9种模型计算的井底压力和实测井底压力,结果见图 7。
|
| 图 7 9种模型的井底压力计算值与实测值对比 Fig.7 Comparison of calculation results and measured values of bottom hole pressure using the 9 models (Govier and Fogarasi气田) (Govier and Fogarasi gas field) |
从图 7可以发现:Mukherjee-Brill模型、Hagedorn-Brown模型、Beggs-Brill模型、Duns-Ros模型、Gray模型和Orkiszewski模型的计算结果和实测井底压力均比较接近;Ansari模型、Govier-Aziz-Fogarasi模型和No-Slip模型的计算结果与实测井底压力相比更为接近。
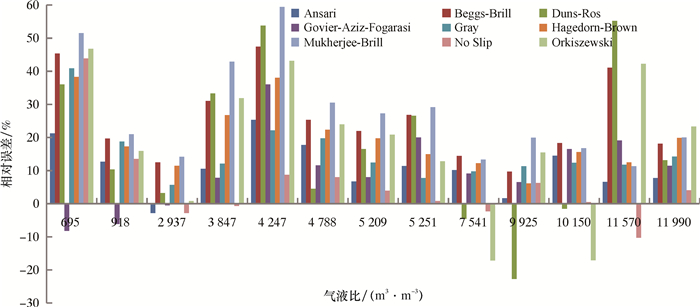
不同气液比条件下,9种计算模型的相对误差分布如图 8所示。
|
| 图 8 不同气液比时9种模型的相对误差分布 Fig.8 Relative error of the 9 models under different gas-liquid ratios (Govier and Fogarasi气田) (Govier and Fogarasi gas field) |
从图 8可看出,气液比在918和4 247 m3/m3附近相对误差变化较为明显。经过分析整理,得到不同气液比条件下精度较高的计算模型:气液比在695~11 990 m3/m3范围内,Ansari模型、Govier-Aziz-Fogarasi模型和No-Slip模型的误差较小,其中No-Slip模型的平均相对误差最小,为5.66%;当气液比小于918 m3/m3时,Govier-Aziz-Fogarasi模型的平均相对误差为7.16%,精度最高,其次是Ansari模型,平均相对误差为16.97%;气液比为918~4 247 m3/m3时,No-Slip模型的平均相对误差为1.72%,精度最高,其次是Ansari模型,平均相对误差为11.02%;当气液比大于4 247 m3/m3时,No-Slip模型、Duns-Ros模型和Ansari模型的误差均较小,其中No-Slip模型平均相对误差最小,为1.38%。
2 模型的优选将气液比的范围划分为5个区间,对比9个气液两相流压降计算模型的平均相对误差,结果如表 1所示。
| 计算模型 | 气液比/(m3·m-3) | ||||
| ≤918 | (918,1 698] | (1 698,2 403] | (2 403,7 997] | ≥7 997 | |
| Ansari | 23.72 | 11.28 | 11.34 | 7.20 | 6.33 |
| Beggs-Brill | 33.87 | 12.85 | 16.25 | 15.45 | 16.32 |
| Duns-Ros | 28.37 | 6.91 | 14.03 | 11.38 | 11.16 |
| Govier-Aziz-Fogarasi | 9.04 | 3.84 | 15.11 | 8.40 | 9.76 |
| Gray | 44.83 | 10.77 | 6.07 | 8.38 | 7.93 |
| Hagedorn-Brown | 18.22 | 1.70 | 5.79 | 12.12 | 10.28 |
| Mukherjee-Brill | 44.20 | 17.59 | 15.90 | 18.53 | 14.58 |
| No-Slip | 24.10 | 6.07 | 3.12 | 2.75 | 1.14 |
| Orkiszewski | 61.59 | 16.01 | 15.36 | 10.49 | 11.50 |
根据表 1的对比结果,推荐如下:连续管排水采气井的气液比小于918 m3/m3时,使用Govier-Aziz-Fogarasi模型;连续管排水采气井的气液比在918~1 698 m3/m3范围内,使用Hagedorn-Brown模型;连续管排水采气井的气液比大于1 698 m3/m3时,使用No-Slip模型。
3 结束语依据121组不同管径连续管排水采气井的实测数据,对9种常用气液两相流压降计算模型进行评价,优选出不同气液比范围内计算精度高的压降模型。对于气液比小于918 m3/m3的低气液比连续管排水采气井,推荐采用Govier-Aziz-Fogarasi模型,对于气液比在918~1 698 m3/m3范围内的低气液比连续管排水采气井,推荐采用Hagedorn-Brown模型,对于气液比大于1 698 m3/m3的高气液比连续管排水采气井,推荐采用No-Slip模型。该研究成果不仅可以提高连续管排水采气井井筒流体压力预测的准确性,还为提高连续管排水采气工艺设计与排液效果分析水平提供相应的理论基础。
| [1] |
明瑞卿, 贺会群, 胡强法. 考虑水平段长度与储层倾角的边水气藏见水时间预测新模型[J].
科学技术与工程, 2018, 18(5): 45-49.
MING R Q, HE H Q, HU Q F. A new model to predict water breakthrough time in edge-water gas reservoirs by considering horizontal length and reservoir dip[J]. Science Technology and Engineering, 2018, 18(5): 45-49. DOI: 10.3969/j.issn.1671-1815.2018.05.008 |
| [2] |
明瑞卿, 贺会群, 唐纯静, 等. 国内外连续管软件研究分析[J].
石油钻采工艺, 2017, 39(6): 771-780, 794.
MING R Q, HE H Q, TANG C J, et al. Study and analysis on domestic and foreign software related with coiled tubing[J]. Oil Drilling & Production Technology, 2017, 39(6): 771-780, 794. |
| [3] |
周舰, 罗懿, 刘岳龙, 等. 大牛地水平井速度管排液工艺研究与应用[J].
石油机械, 2013, 41(12): 102-105.
ZHOU J, LUO Y, LIU Y L, et al. Research and application of velocity string drainage technology in horizontal wells of Daniudi[J]. China Petroleum Machinery, 2013, 41(12): 102-105. |
| [4] |
赵彬彬, 李丽, 白晓弘, 等. 水平井速度管柱排水采气技术研究与试验[J].
石油机械, 2018, 46(1): 88-91, 99.
ZHAO B B, LI L, BAI X H, et al. Research and test on water drainage gas recoveryvelocity string technology for horizontal well[J]. China Petroleum Machinery, 2018, 46(1): 88-91, 99. |
| [5] |
明瑞卿, 贺会群, 唐纯静, 等. 连续管检测监控技术[J].
特种油气藏, 2017, 24(3): 164-169.
MING R Q, HE H Q, TANG C J, et al. Detection and supervision techniques of coiled tubing[J]. Special Oil & Gas Reservoirs, 2017, 24(3): 164-169. DOI: 10.3969/j.issn.1006-6535.2017.03.032 |
| [6] |
钟晓瑜, 颜光宗, 黄艳, 等. 连续油管深井排水采气技术[J].
天然气工业, 2005, 25(1): 111-113.
ZHONG X Y, YAN G Z, HUANG Y, et al. Technology of gas recovery by water drainage for deep wells with coiled tubing[J]. Natural Gas Industry, 2005, 25(1): 111-113. DOI: 10.3321/j.issn:1000-0976.2005.01.032 |
| [7] |
赵彬彬, 白晓弘, 陈德见, 等. 速度管柱排水采气效果评价及应用新领域[J].
石油机械, 2012, 40(11): 62-65.
ZHAO B B, BAI X H, CHEN D J, et al. Effect assessment of drainage gas recovery through velocity string and its new application area[J]. China Petroleum Machinery, 2012, 40(11): 62-65. |
| [8] |
余淑明, 田建峰. 苏里格气田排水采气工艺技术研究与应用[J].
钻采工艺, 2012, 35(3): 40-43.
YU S M, TIAN J F. Application of drainage gas recovery technology in Sulige gas field and its development[J]. Drilling & Production Technology, 2012, 35(3): 40-43. DOI: 10.3969/J.ISSN.1006-768X.2012.03.12 |
| [9] |
宋玉斌, 祁英会, 张珑, 等. 塔里木盆地塔中气田速度管柱排水采气试验效果分析[J].
天然气地球科学, 2015, 26.
SONG Y B, QI Y H, ZHANG L, et al. Analysis of the effect of gas recovery test on the velocity pipe string of Tazhong gasfield, Tarim Basin[J]. Natural Gas Geoscience, 2015, 26(S2): 198-201. DOI: 10.11764/j.issn.1672-1926.2015.S2.0198 |
| [10] |
王晓军, 李俊杞, 孙云超, 等. 强抑制水基钻井液在连续管侧钻井中的应用[J].
石油钻采工艺, 2018, 40(1): 33-39.
WANG X J, LI J Q, SUN Y C, et al. Application of strong-inhibition water based drilling fluid to side tracking of coiled tubing[J]. Oil Drilling & Production Technology, 2018, 40(1): 33-39. |
| [11] |
李猛, 贺会群, 苏堪华, 等. 连续管定向工具工作原理及工具面角度调整分析[J].
钻采工艺, 2017, 40(1): 7-10.
LI M, HE H Q, SU K H, et al. Working principle of coiled tubing orienter and analysis on tool faceorientation[J]. Drilling & Production Technology, 2017, 40(1): 7-10. DOI: 10.3969/J.ISSN.1006-768X.2017.01.02 |
| [12] | ANSARI A M, SYLVESTER N D, SARICA C, et al. A comprehensive mechanistic model for upward two-phase flow in wellbores[R]. SPE 20630, 1994. |
| [13] | BEGGS H D, BRILL J P. A study of two-phase flow in inclined pipes[J]. Journal of Petroleum Technology, 1973, 25(5): 607-617. DOI: 10.2118/4007-PA |
| [14] | DUNS H JR, ROS N C J. Vertical flow of gas and liquid mixtures in wells[R]. WPC 10132, 1963. |
| [15] | AZIZ K, FOGARASI M, GOVIER G W. Pressure-drop in wells producing oil and gas[J]. Journal of Canadian Petroleum Technology, 1972, 11(3): 38-48. |
| [16] | ANON. User manual of API 14B subsurface controlled safety valve sizing computer program[EB/OL].[2010-12-07]. https: //wenku.baidu.com/view/6098f408581b6bd97f19ea76.html. |
| [17] | HAGEDORN A R, BROWN K E. Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits[J]. Journal of Petroleum Technology, 1965, 17(4): 475-484. DOI: 10.2118/940-PA |
| [18] | MUKHERJEE H, BRILL J P. Pressure drop correlations for inclined two-phase flow[J]. Journal of Energy Resources Technology, 1985, 107(4): 549-554. DOI: 10.1115/1.3231233 |
| [19] | KABIR C S, HANSAN A K. A study of multiphase flow behavior in vertical oil wells: PartⅡ-field application[R]. SPE 15139, 1986. |
| [20] | ORKISZEWSKI J. Predicting two-phase pressure drops in vertical pipe[J]. Journal of Petroleum Technology, 1967, 19(6): 829-838. DOI: 10.2118/1546-PA |
| [21] |
陈德春, 徐悦新, 孟红霞, 等. 气井气液两相管流压降计算模型评价与优选[J].
断块油气田, 2017, 24(6): 840-843.
CHEN D C, XU Y X, MENG H X, et al. Evaluation and optimization of pressure drop calculation models for gas-liquid two-phase pipe flow in gas well[J]. Fault-Block Oil and Gas Field, 2017, 24(6): 840-843. |
| [22] | GAITHER O D, WINKLER H W, KIRKPATRICK C V. Single-and two-phase fluid flow in small vertical conduits including annular configurations[J]. Journal of Petroleum Technology, 1963, 15(3): 309-320. DOI: 10.2118/441-PA |
| [23] | RENDEIRO C M, KELSO C M. An investigation to improve the accuracy of calculating bottomhole pressures in flowing gas wells producing liquids[R]. SPE 17307, 1988. |



