0 引言
同一井场钻多口井,可实现重复、批量化作业的“井工厂”钻井模式,该钻井模式已经获得国内业界的广泛认可[1-2]。钻机整体平移设备正是实现这一钻井模式的核心技术设备。目前针对现役的机械钻机和混合动力钻机由于布局分散及结构庞大等不利因素,主要采用轨道步进式钻机平移设备,通过液压缸推动钻机平移导轨上的棘爪步行器实现钻机滑动摩擦型式的整体平移[3]。轨道步进式钻机平移设备由于应用环境复杂苛刻,现场应用中存在着导轨滑移平面变形、磨损严重、步行器棘爪座撕裂、卡爪及固定螺钉断裂变形等问题[4-5],影响了钻机平移设备的使用寿命及平移效率。
目前,轨道步进式钻机平移设备的平移导轨结构优化与数值仿真等方向都获得了大量的理论研究,并进行了现场应用实践[5],但对于棘爪步行器的设计计算大多依靠经验与数值解,专题研究还很少,棘爪步行器力学行为分析作为其设计依据与出发点很有必要进行研究。鉴于此,笔者首次采用力系简化方法,利用力及力矩平衡原理对石油钻机平移用棘爪步行器受力行为进行系统的分析与研究,以获得棘爪步行器受力精确解析值及相关影响因素,这对解决石油钻机平移棘爪步行器工程实际问题具有一定的指导意义。
1 结构棘爪步行器主要由棘爪座、棘爪、棘爪连接销轴、卡爪和卡爪固定螺钉等组成[6],如图 1所示。
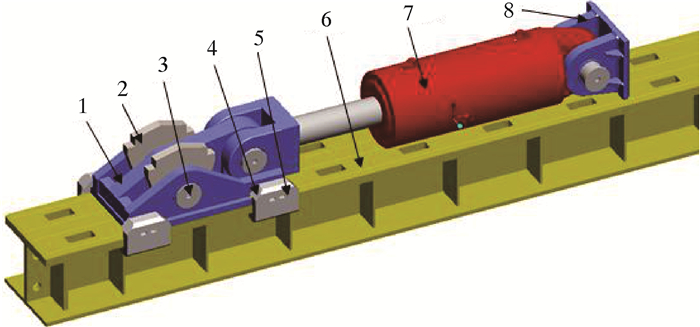
|
| 图 1 棘爪步行器总成 Fig.1 Pawl walker assembly 1—棘爪座;2—棘爪;3—棘爪连接销轴;4—卡爪;5—卡爪固定螺钉;6—导轨;7—液压缸;8—耳座。 |
棘爪座采用调质处理的铸造结构,卡爪采用锻造工艺通过螺钉与棘爪座连接在一起,承载步行器竖直方向分力,限制步行器在钻机平移导轨平面法向移动。钻机平移过程中步行器通过棘爪与平移导轨棘爪孔面配合,实现相连端液压缸的固定,液压缸伸出或收缩带动与其相连接的连接耳座实现钻机平移导轨方向的移动[7]。
2 力学分析模型简化与求解 2.1 受力分析钻机推移过程中,棘爪步行器首先在液缸拉力作用下沿导轨面滑移,直到步行器棘爪作用面滑入导轨面上的棘爪孔内,此时液缸进行反向推力作用,棘爪作用面与导轨面上的棘爪孔面进行接触,产生一个沿接触点到棘爪连接销轴中心方向的作用力,限制了步行器在导轨轴向的滑移。在液缸推力作用下,棘爪受力通过棘爪连接销轴传递给棘爪座及与其相连的卡爪,使步行器整体绕棘爪与导轨接触点转动,直至卡爪与导轨面接触作用,导轨面对卡爪的作用力平衡对棘爪产生的竖直方向分力,最终保持步行器整体的力系平衡,完成液缸在步行器连接端的固定,与其相连接的耳座在液缸推液力作用下带动钻机整体推移运动。钻机拉移过程与推移过程相似,在液缸拉力作用下通过步行器棘爪另一侧作用面与平移导轨作用。
从上述棘爪步行器运动过程分析发现,棘爪步行器在钻机平移过程中受到液压缸作用力F液, 将棘爪简化成二力杆,则平移导轨面对棘爪的作用力为F棘,平移导轨面对前、后卡爪的作用力分别为P1、P2, 分析中忽略导轨自身变形对步行器的影响,步行器在这些力的共同作用下实现空间力系平衡。棘爪步行器在钻机平移过程中的受力如图 2所示。图中m为步行器液缸连接销轴中心高,n为步行器棘爪连接销轴中心高,t为步行器棘爪作用面水平有效距离,O为步行器棘爪连接销轴中心点,O1为步行器液缸连接销轴中心点,O2为步行器棘爪与导轨棘爪孔作用点,L1为步行器棘爪连接销轴中心到前卡爪端点水平距离,L2为步行器棘爪连接销轴中心到后卡爪端点水平距离,L3为步行器棘爪连接销轴中心到液缸连接销轴中心水平距离,θ为液缸安装偏差角。
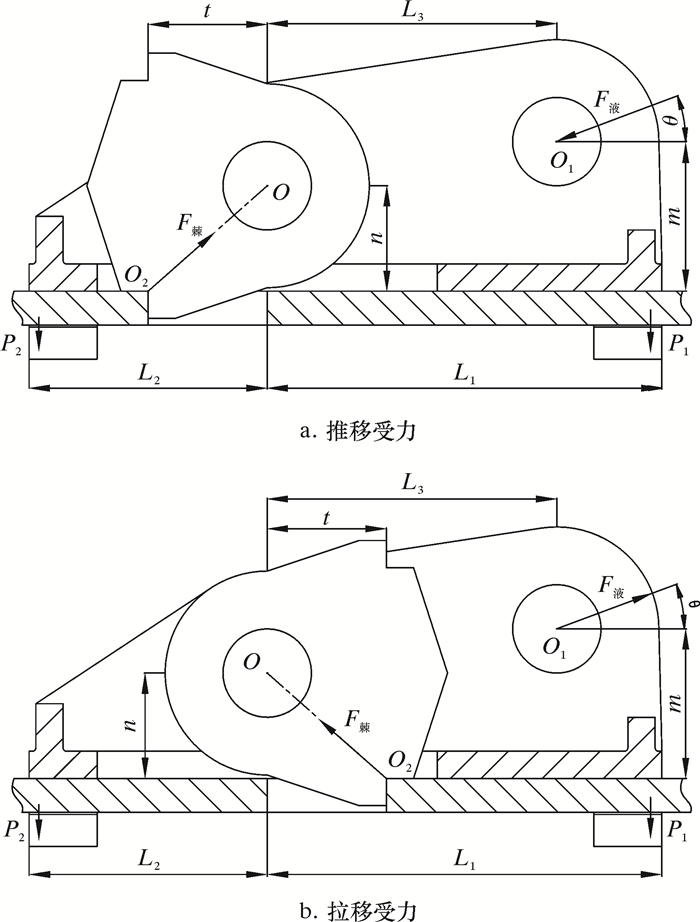
|
| 图 2 棘爪步行器受力示意图 Fig.2 Schematic diagram of the force on the pawl walker |
2.2 力学模型简化
在棘爪步行器受力分析中不考虑其自身变形的影响,将其作为刚体空间力系平衡受力问题研究,考虑其在导轨法向对称面的几何结构与受力情况的对称性,将棘爪步行器空间力系问题简化为平面力系问题。以棘爪步行器几何对称面为受力平面,以棘爪连接销轴中心点O为简化中心,利用力的平移原理,针对推移与拉移状态下,分别将棘爪步行器受力逐一向简化中心平移,力平移后产生一个与原力等价的力和一个相应的力偶作用,最终建立棘爪步行器简化中心的简化平面力系计算模型。棘爪步行器平面力学计算模型如图 3所示。图中MF液为液缸液力对O点平移产生的附加力矩,MF液=F液(m-n)cosθ-F液L3sinθ;MP1为导轨面对前卡爪作用力对O点平移产生的附加力矩,MP1=P1L1;MP2为导轨面对后卡爪作用力对O点平移产生的附加力矩,MP2=P1L1。
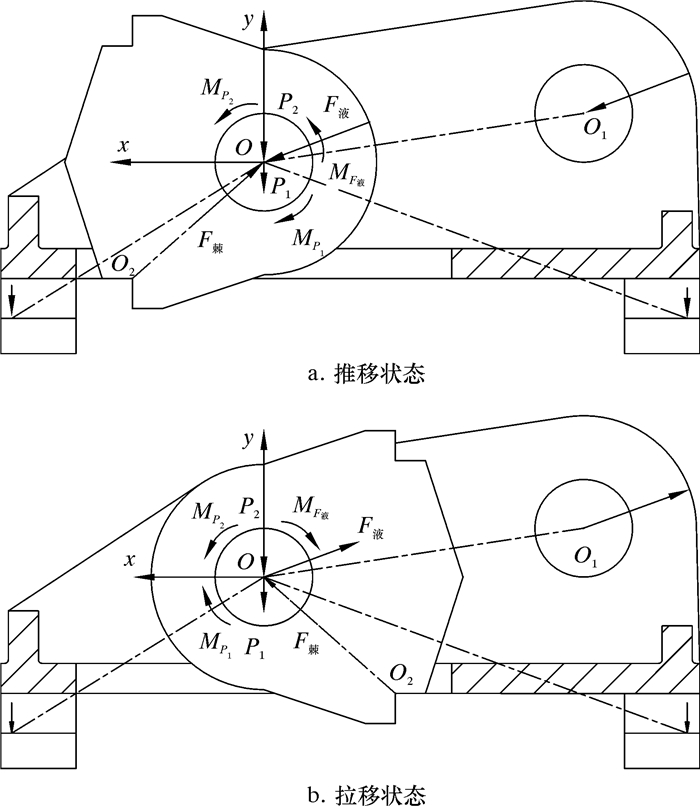
|
| 图 3 棘爪步行器力学计算模型 Fig.3 Mechanical calculation model of the pawl walker |
对棘爪步行器力学简化计算模型依据平面力系平衡条件,分别对图 3中棘爪步行器推移与拉移2种状态下对简化中心O点建立力、力矩平衡方程式,棘爪步行器推移状态下平衡方程如式(1)所示。
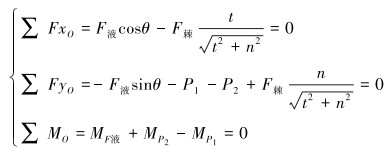
|
(1) |
拉移状态下平衡方程如式(2)所示。
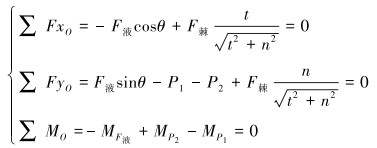
|
(2) |
将各个参数代入上述棘爪步行器平衡方程公式(1)与公式(2),分别对其推移与拉移状态下导轨面对棘爪的作用力进行求解,获得相同值的棘爪力F棘的解析值公式,如式(3)所示。

|
(3) |
式中:F液cosθ为液缸液力水平分力。
从式(3)发现,无论钻机是推移还是拉移过程,步行器棘爪力都为定值,与所平移的钻机载荷呈线性关系。这是因为在钻机平移过程中,液缸液力水平分力用于克服钻机在平移导轨面上摩擦阻力,对于同一钻机其为定值;在平移中钻机载荷为定值情况下,棘爪力随n值的增大而相应增大,随t值的增大而相应减小,因此加大步行器t值有利于改善棘爪的受力情况。
求解式(1)与式(2),同时获得钻机推移及拉移状态下导轨面对前、后卡爪作用力P1、P2的解析公式。
钻机推移过程卡爪力如式(4)和式(5)所示。钻机拉移过程卡爪力如式(6)和式(7)所示。
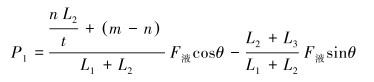
|
(4) |
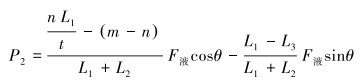
|
(5) |
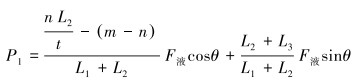
|
(6) |
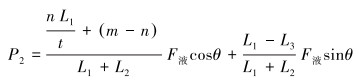
|
(7) |
式中:F液sinθ为液缸液力竖直分力。
从棘爪步行器卡爪力解析公式发现,卡爪力是液缸液力水平分力F液cosθ和液缸液力竖直分力F液sinθ与步行器结构参数间的非线性关系组合,液缸液力竖直分力由液压缸安装偏差造成,从而说明安装偏差对卡爪力产生一定的影响,影响量由竖直分力大小决定。
下面将针对具体实例进一步分析与卡爪力相关的影响因素。目前国内一些钻机平移采用的棘爪步行器几何结构尺寸如表 1所示。
| m | n | t | L1 | L2 | L3 |
| 0.220 | 0.155 | 0.170 | 0.350 | 0.580 | 0.425 |
3 力学行为实例分析 3.1 液缸液力对卡爪力的影响
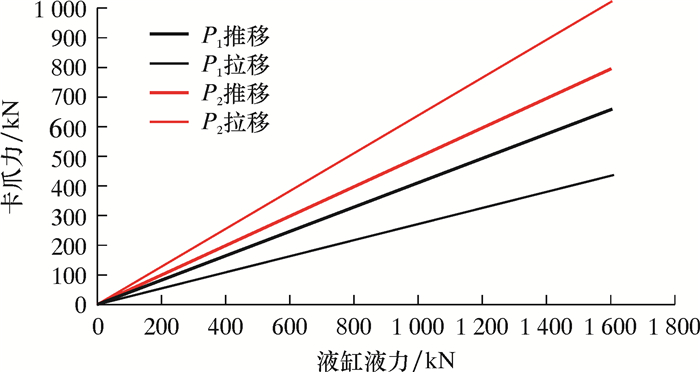
在不考虑液缸安装偏差影响即θ=0°时,将棘爪步行器表 1中结构参数带入前、后卡爪作用力P1、P2的解析式(4)~式(7),获得棘爪步行器在钻机推移与拉移过程中卡爪力与液缸液力关系,如图 4所示。
|
| 图 4 棘爪步行器卡爪力与液缸液力关系图 Fig.4 Relationship between the claw force of the pawl walker and the hydraulic force of the hydraulic cylinder |
分析结果表明:无论钻机是推移还是拉移过程,棘爪步行器卡爪力P1与P2都随液缸液力增加而线性增加;卡爪力为正值,表明钻机平移过程中平移导轨面始终紧贴卡爪;后卡爪力P2平移过程中都大于前卡爪力P1。这一结果与棘爪步行器现场应用相吻合,进一步验证了笔者计算模型的合理性。
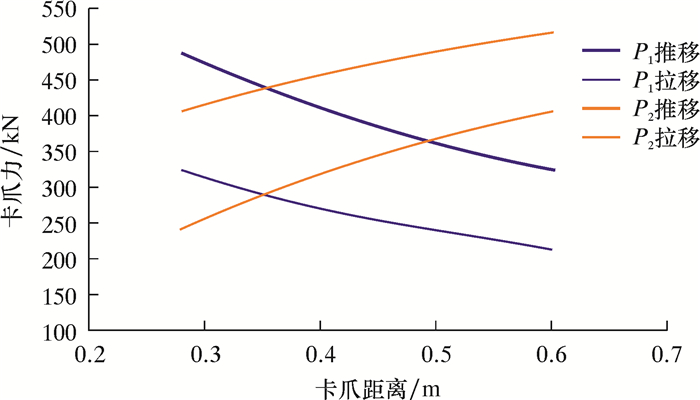
3.2 卡爪位置对卡爪力的影响在不考虑液缸安装偏差影响即θ=0°时,通过对棘爪步行器本身结构参数对卡爪力的影响应用实践分析发现,前卡爪位置即步行器棘爪连接销轴中心到前卡爪端点水平距离L1具有较大的差异可变性。在液缸液力F液=750 kN的定值作用下[8],以卡爪位置L1为变量,分别求解钻机平移过程中卡爪力P1与P2,最终获得棘爪步行器卡爪力与卡爪距离L1之间的关系,如图 5所示。
|
| 图 5 棘爪步行器卡爪力与卡爪距离关系图 Fig.5 Relationship between the claw force and the claw distance of the pawl walker |
分析结果表明:无论钻机是推移还是拉移过程,棘爪步行器前卡爪力P1都随卡爪距离L1增加而非线性降低;后卡爪力P2都随卡爪距离L1增加而非线性增加;卡爪距离L1存在2个分区点,即L1=0.35 m与L1=0.50 m处,由于步行器结构特点对于小于0.35 m结构无法实现,对于2点之间区域,钻机推移过程前卡爪力P1大于后卡爪力P2,钻机拉移过程前卡爪力P1小于后卡爪力P2,对于0.50 m点外区域,钻机平移过程中后卡爪力P2始终大于前卡爪力P1,本实例棘爪步行器L1值就处于0.50 m点外区域,这与上述实例图 4结论一致。
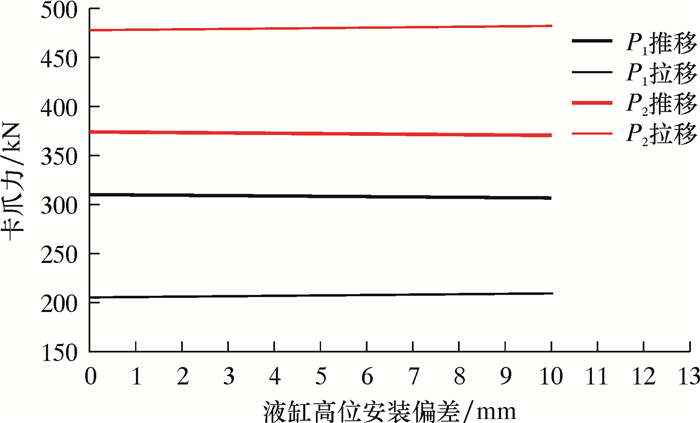
3.3 液缸安装偏差对卡爪力的影响棘爪步行器在钻机井场采用配装型式,由于井场钻机结构及实际安装条件不利于液缸位置的精确安装,造成液缸钻机连接端或高或低的偏差问题。前面分析都是在不考虑液缸安装位置偏差影响即θ=0°时,下面将对棘爪步行器在液缸液力F液=750 kN的定值作用下,分析液缸安装偏差对卡爪力的影响规律。
液缸高位安装偏差值经等价变换为θ值,代入卡爪力计算式(4)~式(7),求解得到钻机平移过程中液缸高位安装偏差与棘爪步行器卡爪力关系,如图 6所示。
|
| 图 6 棘爪步行器卡爪力与液缸高位安装偏差关系图 Fig.6 Relationship between the claw force of the pawl walker and the installation deviation of the high position of the hydraulic cylinder |
分析结果表明:液缸高位安装使钻机推移过程中步行器卡爪力P1、P2都降低,减少量与偏差值同步,使钻机拉移过程中步行器卡爪力P1、P2都相应增加,即液缸高位安装对钻机推移过程有利。对液缸低位安装进一步计算发现,结果与高位安装相反,即液缸低位安装对钻机拉移过程有利。液缸安装偏差对步行器卡爪力P1、P2增减量很小,偏差量在7 mm内,卡爪力变化量在1%范围内,这是因为液压缸原始长度在1.60 m,伸缩行程0.65 m,安装偏差在7 mm时对液缸安装偏差角θ值影响很小,即sinθ值在0.003 1~0.004 4之间, 相应的液缸液力竖直分力F液sinθ值及影响量就很小,最终反映在与安装偏差为零时相比卡爪力变化量就更小了。因此液缸安装偏差在允许范围内的施工中可以忽略。
4 结论(1) 通过棘爪步行器受力分析与简化,建立了一种获得解析解的棘爪步行器平面力学求解模型。
(2) 棘爪步行器棘爪力大小由结构参数决定且与钻机平移载荷呈线性关系;同时获得及验证了棘爪步行器卡爪力在钻机平移过程中的分布与变化规律。
(3) 棘爪步行器卡爪距离与卡爪力关系分析得到,前卡爪位置0.35与0.50 m附近处存在2个临界分区点,这可为棘爪步行器的结构优化设计提供参考。
(4) 由液缸安装偏差对棘爪步行器卡爪力的影响分析可知,液缸安装偏差在7 mm允许范围内,棘爪力不受影响,卡爪力变化量在1%范围内可以忽略。
| [1] |
刘克强, 梁宏伟, 李新弟. 工厂化作业钻机技术现状及应用[J].
石油机械, 2017, 45(9): 27-31.
LIU K Q, LIANG H W, LI X D. Current situation of factory drilling rig and applications[J]. China Petroleum Machinery, 2017, 45(9): 27-31. |
| [2] |
龙志平, 沈建中. 煤层气"井工厂"钻井模式设计与应用[J].
石油机械, 2016, 44(6): 19-23.
LONG Z P, SHEN J Z. CBM "well factory" drilling pattern design and application[J]. China Petroleum Machinery, 2016, 44(6): 19-23. |
| [3] |
王斌, 邱亚玲, 秦菲. 大吨位钻机同井场整体移运装置的现场试运行[J].
石油和化工设备, 2011, 14(10): 38-40.
WANG B, QIU Y L, QIN F. On-site trial of overall transportation device of heave duty drilling rig[J]. Petro & Chemical Equipment, 2011, 14(10): 38-40. DOI: 10.3969/j.issn.1674-8980.2011.10.012 |
| [4] |
罗震, 王卫刚, 陈灵强, 等. 钻机移动装置导轨变形分析及质量控制[J].
机械工程师, 2013(3): 129-130.
LUO Z, WANG W G, CHEN L Q, et al. Deformation analysis and quality control of guide rail of drilling rig transportation device[J]. Mechanical Engineer, 2013(3): 129-130. DOI: 10.3969/j.issn.1002-2333.2013.03.064 |
| [5] |
熊勇.海洋模块钻机滑轨划痕分析及优化设计[D].成都: 西南石油大学, 2014. XIONG Y. Scratch analysis and optimization design of skid beam of offshore module drilling rig[D]. Chengdu: Southwest Petroleum University, 2014. |
| [6] |
历要海. 棘爪步进式钻机移动装置在南美TARAPOA油田的应用[J].
重庆科技学院学报(自然科学版), 2011, 13(1): 56-57, 75.
LI Y H. Application of pawl step-drill moving device in TARAPOA oilfield of South America[J]. Journal of Chongqing University of Science and Technology, 2011, 13(1): 56-57, 75. DOI: 10.3969/j.issn.1673-1980.2011.01.017 |
| [7] |
曹立天, 徐小鹏, 张友会, 等. 7000 m双向移动模块钻机底座技术分析[J].
石油机械, 2017, 45(4): 7-11.
CAO L T, XU X P, ZHANG Y H, et al. Technical analysis of the substructure of the 7000 m cross-move module drilling rig[J]. China Petroleum Machinery, 2017, 45(5): 7-11. |
| [8] |
韩宇, 丛滋东, 何学起, 等. 蓬莱PL19-3平台钻井模块平移部分液压系统改造[J].
中国修船, 2010, 23(4): 55-56.
HAN Y, CONG Z D, HE X Q, et al. Refitting of hydraulic system on translational moving part of drilling module on Penglai PL19-3 platform[J]. China Shiprepair, 2010, 23(4): 55-56. DOI: 10.3969/j.issn.1001-8328.2010.04.021 |



