2. 常州大学石油工程学院;
3. 榆林学院
2. School of Petroleum Engineering, Changzhou University;
3. Yulin University
0 引言
从20世纪80年代开始,油气资源开发逐步向深海转移,高压低温的环境使海底管道水合物堵塞问题变得更加突出。传统天然气水合物防治方法的局限性越来越明显,管道天然气水合物的抑制策略也在发生转变,新一代的动力学抑制剂和风险管理抑制策略正在逐渐得到重视和应用[1]。液固两相螺旋管流是在管内液固两相流动介质轴向速度上叠加切向速度后,形成的一种特殊流动形态[2],由于切向速度的存在使水合物颗粒能够“悬浮”,轴向速度使其向前输运,两者的结合拓展了水合物的安全流动范围。
目前,相关研究人员从试验和数值模拟方面对螺旋流动特性进行了研究。饶永超等[3]对水平管内短扭带引起的螺旋流涡特性进行了数值模拟,发现水平管内螺旋涡首先在扭带吸力面形成,且形成初期,涡量的大小受主涡影响较大,二次涡形成后,涡量大小主要受二次涡影响。刘雯等[4]对管内螺旋导流板引发的旋流场进行数值模拟,结果表明:与螺旋短扭带相比,螺旋导流板作用下的旋流强度大大增加而衰减速度却变慢。A.F.NAJAFI等[5]利用RSM模型对螺旋流速的衰减进行研究,发现入口区域的起旋类型影响涡流的衰减,且下游螺旋流的衰减主要与雷诺数有关。T.S.MOGAJI等[6]等对内置扭带的螺旋沸腾流动进行试验研究,结果表明:与光管试验数据相比其换热系数和压降损失分别提高了36%和133%。K.NANAN等[7]对打孔扭带进行试验,发现相比于普通扭带,打孔扭带对于减少压降有着不错的效果,但是同时使传热效率下降了。
近年来,许多研究者对传统扭带进行了改造,出现了如中空扭带、短扭带和带钉扭带等[8-10]。这些研究大都集中扭带改造对传热强化和摩擦因子等热力学因素的影响,在考察流体流动特性方面,特别是水合物浆体螺旋流动特性的研究较少。笔者对水合物颗粒在长扭带作用下全程起旋的涡量分布、螺旋流衰减特性及水合物颗粒沉积特性进行数值模拟,以期为更好地拓展水合物安全输送边界提供指导。
1 物理模型笔者研究的长扭带物理模型如图 1所示,扭带厚度不计且与圆管紧密结合,将圆管分成2部分。圆管直径D=24 mm,圆管全长L=2 500 mm。管道流体流动沿z轴正方向,重力方向为y轴负方向。用icem软件对物理模型进行网格划分,网格采用四面体非结构网格。网格划分结果如图 2所示。对近壁面网格进行加密,第1层网格高度为0.2,按比率1.1加密5层。主流区网格大小为4。本次模拟采用3种扭带,扭率Y(扭带螺距与宽度之比)分别为6.2、7.4和8.8,同时设置1组以短扭带局部起旋的水合物颗粒携带作为对比,短扭带段长400 mm。经过网格无关性验证以后,网格总数约为120万。

|
| 图 1 长扭带物理模型 Fig.1 Long twisted band physical model |

|
| 图 2 网格划分 Fig.2 Mesh generation |
2 数值模型
建模时做如下假设:①考虑重力的影响;②流体为不可压缩流体;③壁面为固定壁面且温度恒定;④颗粒为圆形球体且颗粒之间为点接触,碰撞过程中无变形;⑤把问题简化为三维、非稳态及常物性的液固两相流动问题。
模拟使用DPM模型(离散相模型),DPM模型是一种欧拉拉格朗日法下的多相流模型,其特点是将颗粒看作离散相,将流体看作连续相。通过跟踪大量分散相颗粒的运动实现分散相与连续相之间的流场耦合。由于将颗粒看成离散相,故离散相颗粒的体积分数较低(一般在10%~12%)。其控制方程如下。
2.1 连续性方程和动量方程连续性方程:
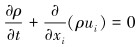
|
(1) |
动量方程:
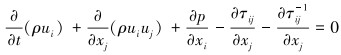
|
(2) |
式中:ρ、u和p分别为流体密度、速度及静压,τij为黏性应力张量,t为时间。
2.2 固相颗粒运动控制方程DPM模型中颗粒轨道通过积分拉氏坐标系下的颗粒作用力微分方程来求解。颗粒的作用力平衡方程(颗粒惯性等于作用在颗粒上的各种力)在笛卡尔坐标系(x方向)下的形式为:

|
(3) |
公式(3)中FD(u-up)表示颗粒的单位质量曳力,FD计算式为:

|
(4) |
颗粒相对雷诺数Re'计算式为:
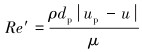
|
(5) |
曳力系数CD计算式为:

|
(6) |
式中:u为流体相速度,up为颗粒速度,μ为流体动力黏度,ρp为颗粒密度,dp为颗粒直径。
a1、a2和a3为常数,当5 000 < Re′ < 10 000时,它们的取值分别为0.46、-490.546及578 700;当Re′大于10 000时,a1、a2及a3的取值分别为0.519 1、-16 625.5及5 416 700。
2.3 湍流运动方程RANS方法是湍流非直接模拟方法中计算量最小的方法。此方法引入雷诺平均法,经过雷诺时均化处理之后,时均流动控制方程组中会产生与-ρ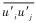

|
(7) |
笔者采用模拟RNG k-ε模型,k-ε涡黏模型一般不直接处理Reynolds应力相,而是引入湍动黏度,然后将湍流应力表示成湍动黏度的函数。而RNG k-ε模型是在k-ε模型的基础上在ε方程中加了附加项,提高了旋转流动计算的准确性。
根据Boussinesq提出的黏涡假设,引入湍动黏度,建立了Reynolds应力相对于平均速度梯度关系式:
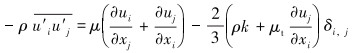
|
(8) |
湍流动能方程及湍流耗散率方程如下:

|
(9) |

|
(10) |
式中:k为湍流动能;μt为湍流黏性系数;δi,j为算子,当i=j时,δi,j=1,当i≠j时,δi, j=0;Rε为附加项。
模型常量取值如下:c1=1.44、c2=1.92、k1=1.0、ε1=1.3。
2.4 边界条件数值模拟软件使用ANSYS 15.0。进口边界采用速度进口条件。液相为水,密度为998.2 kg/m3。固相为水合物颗粒,密度为915 kg/m3,颗粒粒径为0.001 mm,颗粒体积分数设置为10%。进口速度分别选用为3、6和12 m/s。进口温度Tin均为280 K。出口边界采用流量出口。管壁条件采用无滑移固定壁面,设置壁面温度Tw=277 K,同时考虑重力影响。
选取DPM模型对输气管道进行液固两相三维螺旋流瞬态模拟,采用压力基、隐式求解器。控制方程的离散采用有限单元体积法,各标量的离散值采用单元中心点存储。动量分量、湍动能分量和耗散率均采用具有二阶精度的二阶迎风插值格式。压力、速度耦合采用SIMPLEC算法,压力采用多维线性重建方法重建表面压力的二阶格式。在DPM模型中设置固体颗粒的材料及属性、接触模型、喷射速度及喷射位置。定义收敛条件为残差绝对值小于1×10-6。
3 数值计算结果分析 3.1 试验验证为了验证水合物浆体螺旋流动数值模拟结果的准确性,对管道压降进行试验,并将试验结果与模拟结果进行对比。图 3为流体压降随雷诺数(Re)的变化曲线。图中Δp为压降。管道长1.42 m,管径24 mm,颗粒粒径为0.2 mm。雷诺数Re用公式Re=vdρ/μ计算。式中d为管道直径,v为泥沙(颗粒与流体的混合物)流动的平均速度。由图可以看出,在雷诺数(1.0~2.6)×105范围内,模拟结果和试验结果误差在10%以内。验证结果表明:用数值模拟方法可以对水合物颗粒螺旋流动进行模拟预测。

|
| 图 3 雷诺数Re随压降变化曲线 Fig.3 Reynolds number Re versus pressure drop |
3.2 涡量与涡线分布规律
螺旋流是一种特殊的湍流流动,是轴向流动与强制涡的结合。涡量由流场内一点流体质点的角速度所定义,其大小代表了流场中各点旋度的大小,涡量的矢量表达式如下:

|
(11) |
涡量Ω计算式为:

|
(12) |
式中:ω表示流体微团的旋转角速度,i、j、k表示单位矢量,x、y、z表示3个坐标轴。
图 4是管道不同截面处的涡量分布。

|
| 图 4 管道不同位置处涡量分布 Fig.4 Vorticity distribution at different locations of the pipe |
对比图 4a与图 4b可知,长扭带全程起旋时涡量没有衰减,而用短扭带局部起旋时在离开扭带段后涡量迅速衰减。有扭带段均形成2个对称的主涡区,在主涡区由于刚性涡比较稳定,故涡量较小,而靠近边壁处的自由涡区涡量较大。短扭带局部起旋在无扭带段涡量迅速衰减,2个涡核中心先合并成1个,而后迅速耗散,边壁处涡量较全程起旋要小。从图 4b、图 4c及图 4d可以发现,扭率越小涡核中心越集中,涡量尾迹越明显。位于边壁处的颗粒处于自由涡区涡量较大,涡量越大表明流体微团旋转越强烈。故位于边壁处的水合物颗粒自旋强烈,使边壁处水合物不容易团聚。故而全程起旋可以有效延长水合物的输送距离,拓展水合物安全流动边界。
水合物颗粒是否有旋与水合物颗粒运动轨迹无关,而由颗粒自身是否自旋决定。涡线是表征流体各点旋转角速度方向的线,涡线上各质点在同一瞬间的旋转角速度矢量与涡线在该点处相切,故可以从涡线观测水合物颗粒的自旋情况。图 5为不同扭率时颗粒涡线图。

|
| 图 5 不同扭率时颗料涡线图 Fig.5 Vortex diagram of particles at different twist rates |
其中图 5a为局部起旋方式流线图,与图 5b、图 5c及图 5d的全程起旋方式相比,涡线在无扭带区域后颗粒的螺旋前进轨迹有明显的衰减。对比图 5b、图 5c及图 5d的涡线可知,扭率越大,涡线螺距越大,边缘处小圈轨迹越明显。这是因为扭率越小,颗粒螺旋与自旋强度越大,颗粒越容易随着流体以螺旋方式前进,自旋的频率与螺旋前进的频率更能同步。而扭率越大,颗粒自旋与螺旋前进方式越难同步,故扭率越大,涡线外缘旋转小圈越多,水合物携带效率越低。
长扭带将管道分成对称的2个半圆并以螺旋方式前进。由于扭带的作用,迫使流体产生与扭带螺旋方向相同的主涡。图 6是涡线与速度云图。从图中可以观察到涡的形成。涡先在扭带两端形成,由于在扭带压力面的流体最先产生与扭带旋转方向相同的切向速度,故两端速度最高,然后速度中心慢慢偏移到中心近扭带处,旋涡中心也向中心靠扭带处偏移。

|
| 图 6 扭率7.4、Re=24 000时涡线与速度云图 Fig.6 Vortex and velocity distribution under the twist rate of 7.4 and Re=24 000 |
从z=0.02 m处出可以看到涡刚形成还不稳定,随着距离(z轴坐标)的继续向前,在Z=0.10 m处2个对称的涡在近扭带中心附近形成比较稳定的涡。然后近扭带附近的主涡又开始慢慢向壁面偏移,之后开始向两端偏移,同时主涡外围涡线产生明显尾迹。涡的中心在速度中心附近处开始偏移较大,最后在刚性主涡稳定后几乎与速度中心重合。涡的产生加大了流场的扰动,强化了流体间的传热和传质。
3.3 速度与流动分布特性图 7是速度分布初始云图。速度最大值首先出现在管道近扭带远端附近的扭带压力面处,然后速度中心慢慢偏移到中心靠近扭带处,而后形成2个对称的椭圆形中心,随后速度中心开始向边壁处偏移,速度中心开始出现尾迹。这是因为扭带作用在压力面处,迫使流体产生切向速度,而扭带远端半径长,在相同旋转角速度下,远端产生的切向速度较大。随后由于角动量守恒,故在远角端形成的二次涡与主涡旋转方向相反,两端速度减小,速度中心产生偏移。随着主涡的强度变大,边壁处的二次涡逐渐消失。故开始边壁处速度会减小,速度中心向扭带中心偏移,而后由于主涡逐渐稳定,故速度中心又开始向边壁处偏移。

|
| 图 7 扭率7.4、速度12 m/s时速度分布初始云图 Fig.7 Initial velocity distribution under the twist rate of 7.4 and the velocity of 12 m/s |
图 8是不同截面处的速度与矢量图。在速度分布稳定后由图可以观察到速度中心在管道压力面远端处,且有明显尾迹。从矢量线可以看出,切向方向速度先增大,然后稳定,在输送水合物过程中切向速度几乎没有衰减,且在近壁面处切向速度值最大。正是由于切向速度使水合物颗粒与管壁产生较大的切向力,使水合物颗粒不易沉积;同时,切向速度使水合物颗粒自身发生自旋,使水合物颗粒不易团聚而发生沉积,故而大大拓展了水合物的安全流动边界。

|
| 图 8 扭率为6.2时速度与矢量分布云图 Fig.8 Velocity and vector distribution with a twist rate of 6.2 |
图 9为不同起旋方式下的流线图。由图 9a可知,速度中心在管道中心位置处,流线呈水平直线。图 9b中开始部分在扭带的作用下产生螺旋流,速度中心为对称结构,之后由于没有扭带螺旋流迅速衰减,2个速度中心合并成1个,最终螺旋流完全衰减,变为普通平直流后速度分布大致和无扭带相同。从图中流线可以明显看到螺旋流旋流数在离开扭带后迅速衰减。由图 9c可知,速度出现2个速度中心,由于全程起旋故螺旋流没有衰减,2个对称的速度中心呈“太极”状,有明显尾迹。这是因为扭带压力面施加的压力使流体产生切向速度,相同旋转角速度下扭带边缘处产生的线速度最大,故速度中心在扭带压力面附近,同时是持续产生切向速度,故切向速度几乎不衰减,所以产生尾迹。图中螺旋流线呈良好的螺旋状,旋流数几乎保持不变且没有衰减,故长扭带能更好地保持螺旋流强度,以提高水合物的运输效率。

|
| 图 9 不同起旋方式下的流线图 Fig.9 Streamline diagram under different spinning-up patterns |
图 10是不同扭率起旋下的单根流线图。图 10a是短扭带起旋的单根流线图。与长扭带全程起旋相比,螺旋流衰减明显,在脱离扭带的管段,螺距变长,螺旋幅度半径变小。故水合物携带效率下降。由图 10b、图 10c和图 10d可以看出,扭率越小,螺距越小,旋流数越大,且全程螺旋流强度几乎没有衰减;同时螺旋流的流线轨迹呈周期性运动。旋流幅度半径先变大,在接近管道半径后又突然变小,然后又逐渐变大,如此循环,而螺距几乎不变。

|
| 图 10 不同扭率起旋下的单根流线图 Fig.10 Single streamline diagram under different twist rates |
这是因为颗粒撞击壁面后切向速度变小,径向速度甚至会反向,而轴向速度变化较小,故旋流半径变小,螺距不变。同时因为是长扭带全程起旋,故在长扭带作用下切向速度和径向速度又逐渐增大,如此反复循环。
3.4 水合物浆体质量浓度分布图 11是对称的2个水合物颗粒的运动轨迹图。从图可以看出,扭带将管道分成对称的2个半圆,2个水合物颗粒分别从对称半圆入口射入,其运动轨迹呈现良好的螺旋线形方式前进。由于是长扭带全程起旋,可以保证螺旋流强度不会衰减。故水合物颗粒从进入到流出管道都能保持螺旋线方式前进。

|
| 图 11 水合物颗粒运动轨迹图 Fig.11 Trajectory diagram of hydrate particles |
图 12是不同时刻的水合物颗粒停留时间分布图。

|
| 图 12 不同时刻的水合物颗粒停留时间分布图 Fig.12 Hydrate particle residence time distribution at different times |
从图 12可以看出,水合物颗粒在起始阶段由于螺旋流还不稳定,故颗粒整体运动方式不明显,特别是在水合物质量浓度较高的初始区域。而随着距离的增加,螺旋流强度逐渐趋于平稳,水合物颗粒集中在2个对称的旋涡中心,并以双螺旋线方式输运出管道。从图 12a可以看出,以明显螺旋流动前进的范围较小,水合物颗粒在其前端质量浓度较小处螺旋运动方式较为明显,随着运动时间的延长,运动距离变远,螺旋流在长扭带连续起旋下螺旋流逐渐区于稳定,明显螺旋输送段区域变长。
图 13为不同位置处管道截面中心线上的颗粒质量浓度分布图。水合物颗粒质量浓度成明显的双峰趋势。波峰的位置在主旋流作用下沿着圆心做周期性变换。这是因为涡的作用颗粒集中在旋涡中心处,当波峰较高时受剪切力的作用又会被切断而趋于平缓。因为是长扭带所以螺旋流不会衰减,故水合物颗粒质量浓度会呈周期性波峰堆积而又平缓的过程,使水合物颗粒不易堆积,提高了水合物颗粒的输送能力。

|
| 图 13 不同位置处管道截面中心线上的颗粒质量浓度分布图 Fig.13 Distribution of particle mass concentration at the centerline of the pipe section at different locations |
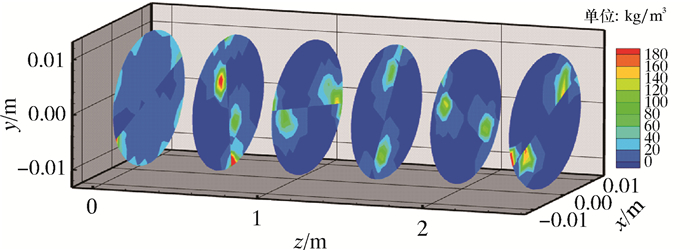
图 14为管道不同位置处水合物颗粒质量浓度分布图。由图可以看出,在初始段水合物颗粒质量浓度分布较为不均匀,初始时颗粒集中在扭带中心位置。随着距离的增加,水合物颗粒质量浓度呈明显的对称分布,水合物颗粒由于离心力被甩到扭带近压力面附近。同时因为该处在螺旋旋涡中心,压力较低,迫使周围颗粒向低压区集中。
|
| 图 14 管道不同截面处颗粒质量浓度分布图 Fig.14 Distribution of particle mass concentration at different cross sections of the pipe |
4 结论
(1) 以长扭带全程起旋涡量几乎不衰减,且扭率越小涡量越大,涡核中心越集中。涡量越大说明流体微团自旋越强烈。水合物颗粒自旋强度越大,颗粒越不易团聚。
(2) 以长扭带起旋的涡先在扭带压力面两端产生,并逐渐向扭带中心移动,稳定后又开始向管壁处偏移,最后涡核中心与速度中心重合。
(3) 与短扭带相比,长扭带切向速度几乎不衰减,且随着距离的增加速度中心产生的尾迹越明显。速度分布中心首先出现在扭带压力面处,然后向扭带中心偏移,稳定后向管道边壁处偏移。
(4) 与短扭带相比,长扭带全程起旋螺旋流几乎不衰减,扭率越小螺旋流强度越高,且流线呈周期性变化。
(5) 水合物颗粒质量浓度呈明显的对称分布,集中在扭带边缘处。随着输送距离的增加,水合物颗粒螺旋输送轨迹越明显。
| [1] |
王武昌, 李玉星, 樊栓狮, 等. 管道天然气水合物的风险管理抑制策略[J].
天然气工业, 2010, 30(10): 69-72.
WANG W C, LI Y X, FAN S S, et al. Hydrate inhibiting policy based on risk management for oil and gas pipelines[J]. Natural Gas Industry, 2010, 30(10): 69-72. |
| [2] |
李建敏, 王树立, 饶永超, 等. 表面活性剂对气液两相螺旋管流流动特性的影响[J].
水动力学研究与进展, 2015, 30(1): 18-23.
LI J M, WANG S L, RAO Y C, et al. Influence of surfactant on flow characteristics of gas-liquid two phase spiral pipe flow[J]. Journal of Hydrodynamics, 2015, 30(1): 18-23. |
| [3] |
饶永超, 常凯, 王树立, 等. 水平管内螺旋流涡特性数值模拟[J].
水动力学研究与进展, 2016, 31(4): 503-509.
RAO Y C, CHANG K, WANG S L, et al. Numerical simulation on vortex characteristics of swirl flow in a horizontal pipe[J]. Journal of Hydrodynamics, 2016, 31(4): 503-509. |
| [4] |
刘雯, 程小莉, 陈勇, 等. 管内螺旋导流板引发的气液两相旋流场[J].
机械工程学报, 2013, 49(22): 164-169.
LIU W, CHENG X L, CHEN Y, et al. Gas-liquid swirling flow induced by helical tape with core-rod inside circular pipe[J]. Journal of Mechanical Engineering, 2013, 49(22): 164-169. |
| [5] | NAJAFI A F, MOUSAVIAN S M, AMINI K. Numerical investigations on swirl intensity decay rate for turbulent swirling flow in a fixed pipe[J]. International Journal of Mechanical Sciences, 2011, 53(10): 801-811. DOI: 10.1016/j.ijmecsci.2011.06.011 |
| [6] | MOGAJI T S, KANIZAWA F T, FILHO E P B, et al. Experimental study of the effect of twisted-tape inserts on flow boiling heat transfer enhancement and pressure drop penalty[J]. International Journal of Refrigeration, 2013, 36(2): 504-515. DOI: 10.1016/j.ijrefrig.2012.10.008 |
| [7] | NANAN K, THIANPONG C, PROMVONGE P, et al. Investigation of heat transfer enhancement by perforated helical twisted-tapes[J]. International Communications in Heat and Mass Transfer, 2014, 52: 106-112. DOI: 10.1016/j.icheatmasstransfer.2014.01.018 |
| [8] | EIAMSA-ARD S, SEEMAWUTE P. Decaying swirl flow in round tubes with short-length twisted tapes[J]. International Communications in Heat and Mass Transfer, 2012, 39(5): 649-656. DOI: 10.1016/j.icheatmasstransfer.2012.03.021 |
| [9] | MURUGESAN P, MAYILSAMY K, SURESH S. Heat transfer and friction factor studies in a circular tube fitted with twisted tape consisting of wire-nails[J]. Chinese Journal of Chemical Engineering, 2010, 18(6): 1038-1042. DOI: 10.1016/S1004-9541(09)60166-X |
| [10] | AIDUN C K, PARSHEH M. Spatially periodic reversing core in a twisted-fin generated swirling pipe flow[J]. Physics of Fluids, 2007, 19(6): 68-71. |




