2. 西安三维应力工程技术有限公司
2. Xi'an Serv Stress Engineering Technology Co., Ltd
0 引言
在定向井及水平井等的作业过程中,造斜井段的套管会受到井眼对套管的弯曲载荷作用,导致套管抗挤强度受到影响,尤其当造斜井段处于异常高压地层时,如盐膏层或其他异常压力井段等,更容易发生套管挤压变形或错断等复杂情况[1-4]。为避免该类情况,保证套管在弯曲载荷下的抗挤强度尤为重要。国内外学者开展的部分弯曲套管抗外挤研究主要集中在理论研究方面[5-8],理论结合试验验证的研究还非常少。
为保证在弯曲载荷状态下的套管抗挤强度满足作业要求,开展弯曲套管抗挤强度的研究非常必要。笔者结合广泛采用的API BUL 5C3标准套管抗挤强度计算公式[9-12],建立了套管在弯曲载荷条件下的抗挤力学模型,结合ANSYS有限元模拟,研究了套管抗挤强度随井眼曲率的变化规律,并在室内条件下建立了套管弯曲载荷下的抗挤试验平台,开展了不同弯曲率下的套管抗挤试验,在同等规格套管条件下,对理论计算结果进行了对比验证。笔者采用理论与试验相结合的方式,研究了套管抗挤强度与弯曲率的关系模型。研究结果为现场弯曲造斜井段的套管抗挤强度设计提供了重要参考,也为复杂井段造斜率的选取提供了借鉴。
1 套管在弯曲载荷下的抗挤强度研究 1.1 弯曲套管力学模型在未施加弯曲载荷时,套管抗外挤强度为与径厚比相关的函数[13-15],套管产生屈服时的外挤力py为:
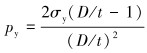
|
(1) |
式中:σy为API名义最小屈服强度,MPa;D为套管名义外径,mm;t为套管名义壁厚,mm。
套管在弯曲井段中的状态等同于在两端施加了与井眼曲率相关的弯曲载荷,在弯曲载荷作用下套管会产生局部轴向应力。以弯曲井段套管的横截面中心为原点建立柱坐标系(ρ,θ,z),得到与弯曲载荷相关的局部轴向应力σz:
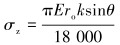
|
(2) |
式中:E为套管钢材的弹性模量;ro为套管外半径,mm;k为每30 m弯曲段井眼曲率,(°);θ为弯曲套管段对应的圆心角,(°)。
根据式(2),当套管呈现90°弯曲,即圆心角达到90°时,弯曲载荷产生最大的轴向应力,为保证套管强度有足够余量,取θ=90°进行计算。由材料力学理论得到弯曲载荷作用下套管所受的径向应力σr及环向应力σθ:
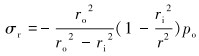
|
(3) |
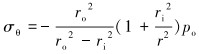
|
(4) |
由Von Mises判别准则,得到套管发生屈服失效的等效应力:
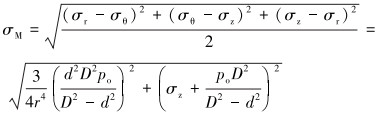
|
(5) |
根据式(5),最大应力发生在套管内壁上,即当r=ri时,套管内壁会发生屈服失效,此时所承受外挤力载荷po为:
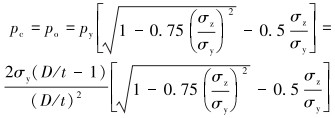
|
(6) |
式中:ri为套管内半径,mm;pc为弯曲载荷作用下的套管抗挤强度,MPa。
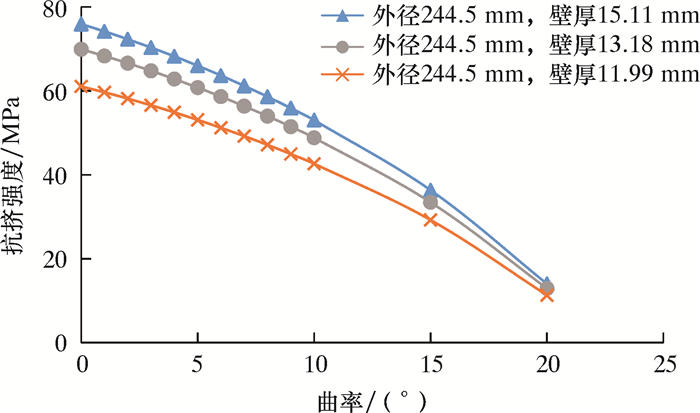
1.2 抗挤强度与曲率关系根据建立的弯曲载荷下套管力学理论模型,以T95钢级ø244.5和ø177.8 mm套管为例,得到不同壁厚条件下,套管抗挤强度随每30 m井段曲率的变化规律,如图 1和图 2所示。
|
| 图 1 ø244.5 mm套管抗挤强度与弯曲率关系曲线 Fig.1 Relationship of collapse strength and curving rate of ø244.5 mm casing |
|
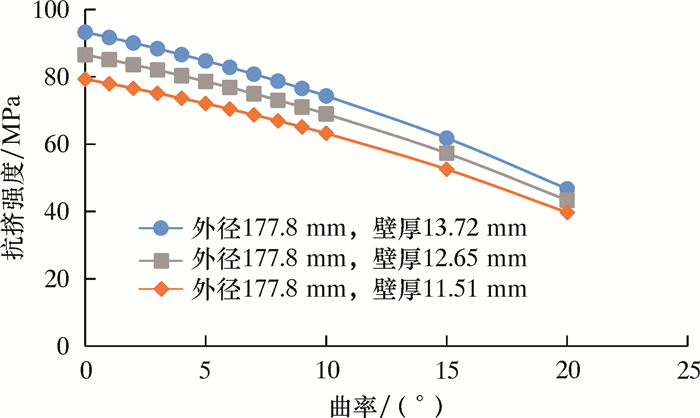
| 图 2 ø177.8 mm套管抗挤强度与弯曲率关系曲线 Fig.2 Relationship of collapse strength and curving rate of ø177.8 mm casing |
由图 1和图 2可知,套管在弯曲载荷条件下,抗挤强度随曲率的增加逐渐下降,实际常用曲率范围内(每30 m井段曲率0°~7°),基本呈现线性下降趋势,当曲率继续增加(>7°),抗挤强度下降趋势越来越快,整体看服从良好二次下降曲率;在钢级和尺寸相同的条件下,套管壁厚越薄,抗挤强度受曲率的影响越小,下降趋势越平缓;以外径244.5 mm的同钢级套管为例,当每30 m井段曲率由0°增加为3°时,壁厚15.11 mm的套管抗挤强度降低5.61 MPa,壁厚为11.99 mm的抗挤强度降低只有4.51 MPa,降幅明显减小。
以外径244.5 mm、壁厚为15.11 mm的套管为例,抗挤强度与弯曲率的关系为:
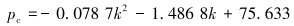
|
(7) |
对于外径244.5 mm、壁厚15.11 mm的套管,非弯曲状态下,计算得到的抗挤强度为75.95 MPa,当曲率增加为3°时,抗挤强度降低为70.34 MPa,降低约5.61 MPa,降幅7.39%;当曲率由10°增加到13°时,抗挤强度由53.03 MPa降低为43.53 MPa,降低约9.50 MPa,降幅17.91%,降低速度明显增加。
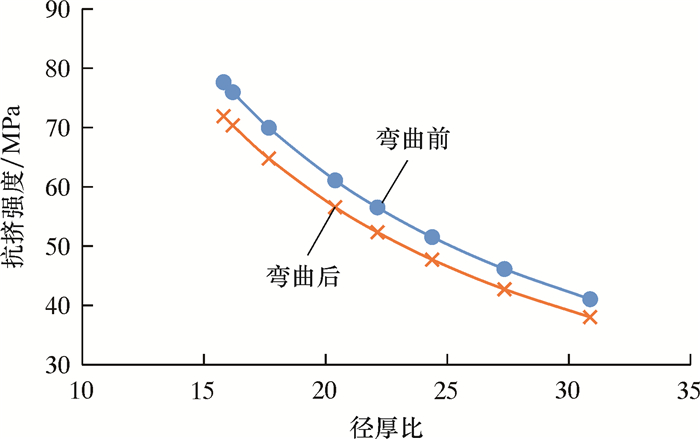
同样以ø244.5 mm同钢级套管为例,根据弯曲套管抗挤理论,得到弯曲前、后(以曲率3°为例)套管抗挤随径厚比的变化规律,如图 3所示。
|
| 图 3 套管弯曲前、后抗挤强度随径厚比变化关系 Fig.3 The relationship between the collapse strength and the diameter -thickness ratio before and after the bend of casing |
由图 3可知,套管抗挤强度随径厚比增加逐渐下降,且下降趋势逐渐平缓,服从良好的二次函数关系;套管施加弯曲载荷抗挤强度与径厚比也服从良好的二次函数关系,当径厚比为15.80时,弯曲前、后抗挤强度差值约为5.74 MPa,当径厚比增大到30.87时,弯曲前、后抗挤强度差值降为3.03 MPa,说明套管弯曲后抗挤强度随径厚比增加而下降的趋势更为平缓。
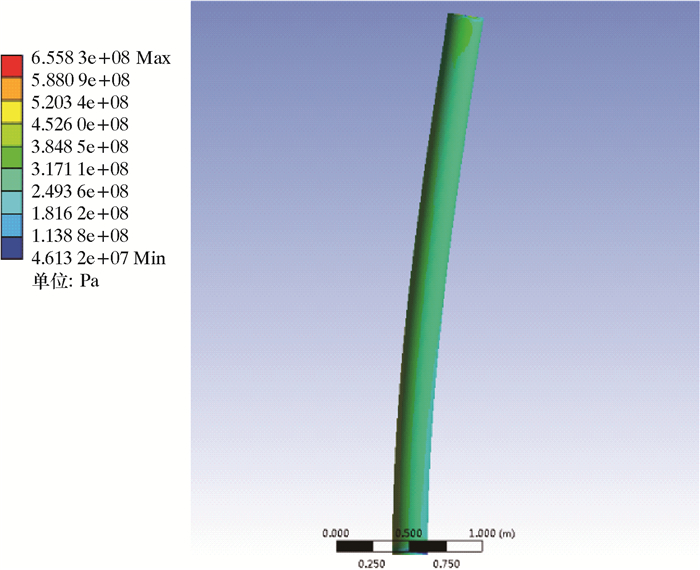
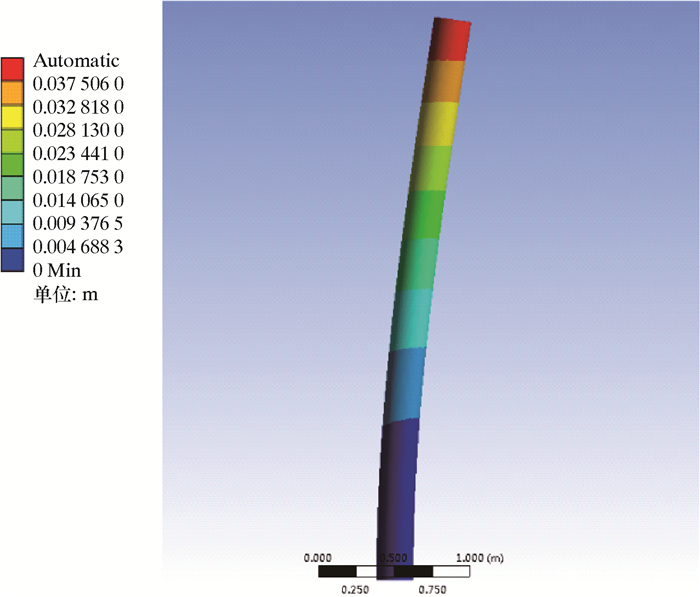
2 有限元分析针对外径244.5 mm、壁厚15.11 mm套管,利用ANSYS有限元软件建立了弯曲载荷条件下套管力学网格模型,套管材料弹性模量取206 GPa,泊松比取0.3,材料类型选择Solide45,模型几何长度2.74 m(大于10倍管外径),与室内试验有效长度保持一致。模型一端固定约束,另一端给予水平位移约束,保证套管模型以一定的曲率弯曲。有限元分析结果如图 4~图 6所示。
|
| 图 4 弯曲套管的等效应力云图 Fig.4 Equivalent stress distribution of the curved casing |
|
| 图 5 弯曲套管的位移云图 Fig.5 Displacement distribution of the curved casing |
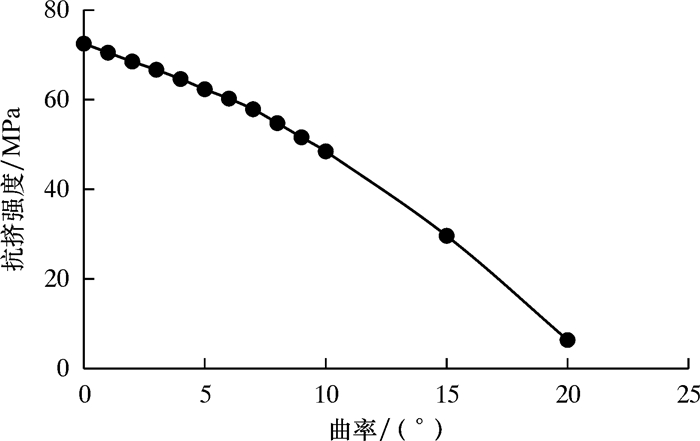
|
| 图 6 套管抗挤强度随曲率变化关系 Fig.6 Relationship between collapse strength of casing and curvature |
根据施加的约束和内外压载荷即可求解出模型各个位置点的等效应力,并得到约束条件和载荷环境下的最大等效应力,当最大等效应力等于材料的屈服极限时,即认为此时施加的外压为弯曲套管的剩余抗外挤强度。
通过ANSYS有限元软件模拟分析,拟合得到套管弯曲后抗挤强度随曲率变化关系如下:
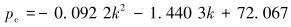
|
(8) |
有限元模拟结果表明:套管抗挤强度随曲率变化服从良好的二次函数关系,随曲率的增大,抗挤强度下降趋势逐渐加快,与通过理论模型计算的结论一致。在现场常用的造斜率范围内(≤7°),理论计算结果与软件模拟结果相差不大,两者最大相差3.68 MPa,误差约为5.57%。
3 弯曲套管试验研究 3.1 试验平台为验证理论计算结果,笔者在室内建立了套管弯曲条件下抗挤强度全尺寸评价系统,如图 7和图 8所示。系统主要由密封套筒、弯曲载荷控制装置、外挤压力控制装置、增压装置、端部密封总成和计算机显示系统等组成。密封试验釜总长约3.80 m,两端密封固定点距离为2.74 m,弯曲支撑点位于固定点中心。
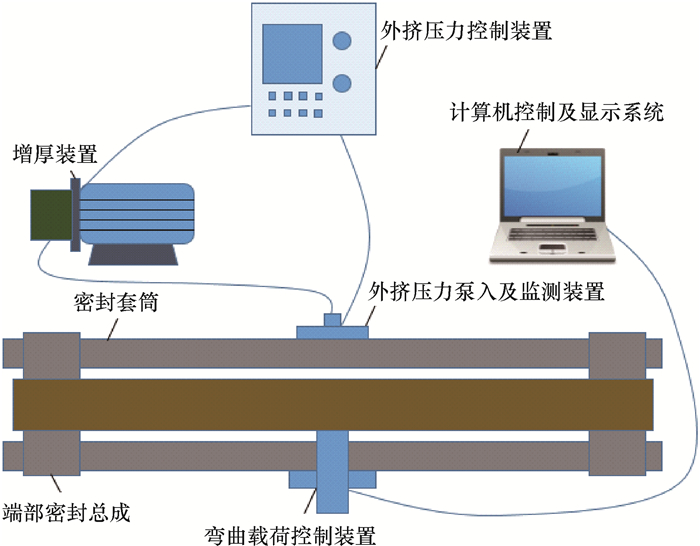
|
| 图 7 室内弯曲套管抗挤试验平台 Fig.7 Indoor collapse test platform for bending casing |

|
| 图 8 弯曲套管抗挤密封套筒实物图 Fig.8 Photo of the sealing sleeve for casing collapse 1—弯曲载荷施加装置;2—外挤载荷泵入装置。 |
在保证密闭的情况下,通过套筒中间的位移施加装备对套管施加弯曲载荷,使套管产生一定位移,从而达到规定的曲率;在套筒与套管环空加水,提供水压以模拟外挤压力,通过伺服设备补充套管曲率的变化,最后在指定曲率下完成套管的外挤破坏,从而达到规定的曲率。
3.2 试验套管曲率的实现试验采用的曲率主要参照现场钻井常用曲率(≤7°),分别取0°、3°、5°和7°,根据套管及油管相关试验标准[16],计算得到实现曲率所需的位移量。
曲率半径计算公式为:
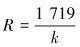
|
(9) |
位移计算公式为:
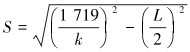
|
(10) |
式中:L为套管长度,m。
由计算可知,当曲率为0°、3°、5°和7°时,相对应的位移分别为0.000、1.638、2.729和3.822 mm。
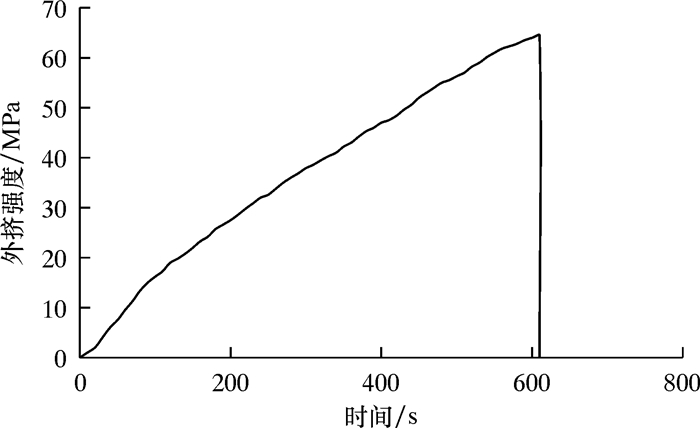
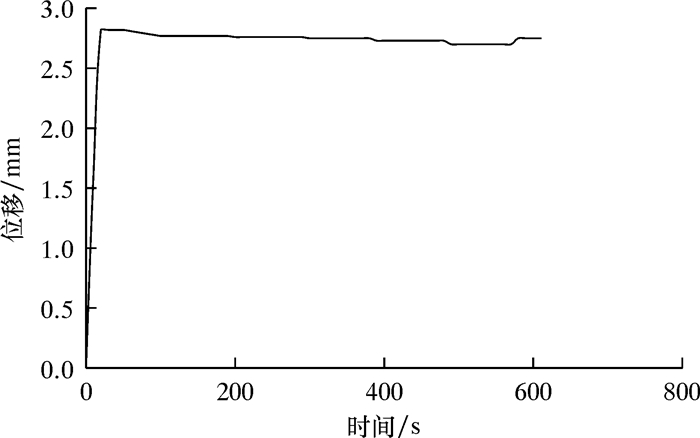
3.3 试验结果弯曲条件下,通过套筒内壁与套管之间的环空逐渐增加水压,直到套管失效,监测到套管失效时临界外挤力即等同于抗挤强度。试验过程中外挤压力曲线及曲率控制曲线分别如图 9和图 10所示。图 11为试验挤毁套管形貌。
|
| 图 9 曲率为5°时外挤压力施加曲线 Fig.9 External pressure applying curve under the curvature of 5° |
|
| 图 10 满足5°曲率的位移控制曲线 Fig.10 Displacement control curve for the curvature of 5° |

|
| 图 11 套管挤毁失效形貌 Fig.11 Casing collapse failure appearance |
根据试验,不施加弯曲载荷下,挤毁试验压力为73.8 MPa,3°曲率下挤毁试验压力为68.3 MPa,5°曲率下挤毁试验压力为64.5 MPa,7°曲率下挤毁试验压力为61.2 MPa。
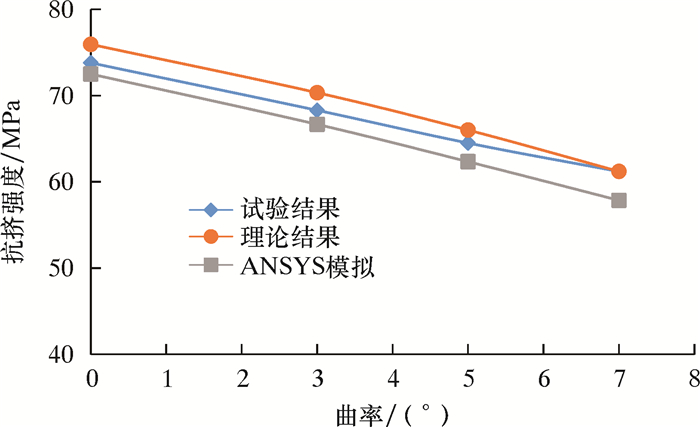
笔者对比分析了理论计算结果、ANSYS模拟结果及室内试验结果,对比结果如图 12所示。
|
| 图 12 理论计算和ANSYS模拟结果与室内试验结果对比 Fig.12 Comparison of theoretical calculation results, ANSYS simulation results and laboratory test results |
由图 12可以看出,在曲率较低的情况下(≤7°),理论计算、ANSYS模拟及室内试验得到的抗挤强度随曲率的变化趋势一致,且有限元模拟结果、室内试验结果与理论计算结果相差很小,有限元模拟结果误差最大为5.57%,试验结果误差最大为2.91%。
4 结论(1) 建立了受弯曲载荷的套管力学模型,研究了套管抗挤强度与曲率、径厚比的关系;弯曲载荷条件下,抗挤强度随曲率的增加逐渐下降,实际常用曲率范围内(0°~7°),基本呈现线性下降趋势,当曲率继续增加(>7°),抗挤强度下降趋势越来越快,整体服从良好的二次函数下降关系;在钢级和尺寸相同的条件下,套管壁厚越薄,抗挤强度受曲率的影响越小,下降趋势越平缓;抗挤强度随径厚比也服从良好的二次函数下降关系,且随着径厚比的增加,抗挤强度下降趋势逐渐平缓。
(2) 建立了弯曲载荷下的套管抗挤强度试验平台,在现场常用曲率范围内(0°~7°),理论计算、ANSYS模拟及室内试验得到的抗挤强度随曲率的变化趋势一致,且有限元模拟结果、室内试验结果与理论计算结果相差很小,有限元模拟结果误差最大为5.57%,试验结果误差最大为2.91%。
| [1] |
徐刚, 刘鹏, 张启龙, 等. 渤海油田典型井套管损坏原因分析[J].
表面技术, 2017, 46(7): 168-172.
XU G, LIU P, ZHANG Q L, et al. Analysis of casing damage on typical wells in Bohai Oilfield[J]. Surface Technology, 2017, 46(7): 168-172. |
| [2] |
房锡业. 复杂条件下油井套管损坏原因及预防措施[J].
油气地质与采收率, 2013, 20(4): 94-98, 101.
FANG X Y. Casing damage analysis and preventing measures under complex conditions[J]. Petroleum Geology and Recovery Efficiency, 2013, 20(4): 94-98, 101. DOI: 10.3969/j.issn.1009-9603.2013.04.024 |
| [3] |
孙一流, 陈勉, 金衍, 等. 塔里木盆地玉科区块超深井膏盐层段套管损坏机理与防治措施[J].
天然气工业, 2016, 36(12): 92-99.
SUN Y L, CHEN M, JIN Y, et al. Damage mechanism of casings used in ultra-deep well salt layers of Yuke Block in the Tarim Basin and prevention measures[J]. Natural Gas Industry, 2016, 36(12): 92-99. DOI: 10.3787/j.issn.1000-0976.2016.12.013 |
| [4] |
练章华, 罗泽利, 于浩, 等. 砂泥岩夹层套管损坏的有限元分析及防控措施[J].
石油钻采工艺, 2016, 38(6): 887-892.
LIAN Z H, LUO Z L, YU H, et al. Finite element analysis and control measures on casing failure in sand shale interbeds[J]. Oil Drilling & Production Technology, 2016, 38(6): 887-892. |
| [5] |
练章华, 罗泽利, 牟凤英, 等. 石油勘探地下套管损坏载荷强度设计研究[J].
计算机仿真, 2017, 34(6): 98-103, 380.
LIAN Z H, LUO Z L, MOU F Y, et al. Research on load strength design of casing damage in oil exploration[J]. Computer Simulation, 2017, 34(6): 98-103, 380. DOI: 10.3969/j.issn.1006-9348.2017.06.021 |
| [6] |
葛伟凤, 陈勉, 金衍, 等. 水平井造斜段盐膏层套管等效应力分析[J].
钻采工艺, 2013, 36(2): 87-89.
GE W F, CHEN M, JIN Y, et al. Analysis of the equivalent stress on casings induced by salt-gypsum creep in build-up sections of horizontal wells[J]. Drilling & Production Technology, 2013, 36(2): 87-89. DOI: 10.3969/J.ISSN.1006-768X.2013.02.25 |
| [7] |
周雄, 何世明, 郭元恒, 等. 非均匀载荷套管抗外挤能力分析[J].
机械设计与制造, 2014(10): 213-216.
ZHOU X, HE S M, GUO Y H, et al. Collapse resistance analysis of casing non-uniform load[J]. Machinery Design & Manufacture, 2014(10): 213-216. DOI: 10.3969/j.issn.1001-3997.2014.10.064 |
| [8] |
祝效华, 罗诗雨. 套管腐蚀缺陷的规则化处理及抗挤强度分析[J].
科学技术与工程, 2017, 17(9): 193-198.
ZHU X H, LUO S Y. The regularization of casing corrosion defects and collapse strength analysis[J]. Science Technology and Engineering, 2017, 17(9): 193-198. DOI: 10.3969/j.issn.1671-1815.2017.09.034 |
| [9] | American Petroleum Institute. API Technical Report 5C3, Technical report on equations and calculations for casing, tubing, and line pipe used as casing or tubing; and performance properties tables for casing and tubing[S]. Washington D C, USA: American Petroleum Institute, 2008. |
| [10] |
郑洋, 薛超, 邓宽海, 等. 非均匀载荷作用下套管弹塑性变形分析[J].
科学技术与工程, 2014, 14(20): 210-214.
ZHENG Y, XUE C, DENG K H, et al. Non-uniform loads analysis of elastic plastic deformation about casing[J]. Science Technology and Engineering, 2014, 14(20): 210-214. DOI: 10.3969/j.issn.1671-1815.2014.20.040 |
| [11] |
徐德奎, 任虎彪, 李明飞, 等. 考虑弯矩和剪切影响的造斜段套管抗挤强度分析[J].
石油机械, 2016, 44(9): 11-14.
XU D K, REN H B, LI M F, et al. Analysis of collapsing strength of casing in buildup section considering bending moment and shear influence[J]. China Petroleum Machinery, 2016, 44(9): 11-14. |
| [12] | TONG H, GUO D Q, ZHU X H. Application of multiphysics coupling FEM on open wellbore shrinkage and casing remaining strength in an incomplete borehole in deep salt formation[J]. Mathematical Problems in Engineering, 2015, 4: 1-9. DOI: 10.1007/978-3-642-17584-8 |
| [13] | HUANG W J, GAO D L. A theoretical study of the critical external pressure for casing collapse[J]. Journal of Natural Gas Science and Engineering, 2015, 27: 290-297. DOI: 10.1016/j.jngse.2015.08.063 |
| [14] | LIN Y H, DENG K H, ZENG D Z, et al. Theoretical and experimental analyses of casing collapsing strength under non-uniform loading[J]. Journal of Central South University, 2014, 21(9): 3470-3478. DOI: 10.1007/s11771-014-2324-6 |
| [15] | DENG K H, LIN Y H, QIANG H, et al. New high collapse model to calculate collapse strength for casing[J]. Engineering Failure Analysis, 2015, 58: 295-306. DOI: 10.1016/j.engfailanal.2015.08.036 |
| [16] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 石油天然气工业套管及油管螺纹连接试验程序: GB/T 21267-2007[S]. 北京: 中国标准出版社, 2008. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Petroleum and natural gas industries-Procedures for testing casing and tubing connections: GB/T 21267-2007[S]. Beijing: Standards Press of China, 2008. |



