0 引言
井漏是钻井过程中的难题之一,漏失压力则是地层漏失性质中的一个重要参数[1-3],合理确定井漏是进行地层防漏堵漏作业的前提,也是钻井液密度合理设计的重要条件。传统的漏失压力模型主要针对完整性地层,认为漏失压力接近于地层破裂压力[4-8],而实际地层中存在层理、节理及微裂缝,其漏失压力真实值远低于传统漏失压力计算值。基于此,笔者采用基于裂缝性地层漏失压力的最小主应力模型、基于统计学的模型及基于临界裂缝宽度的模型,创新性地建立了基于裂缝圆环应力的模型,利用渤中区块裂缝性地层探井实例,将4种裂缝性漏失压力模型分别进行了计算并对比,旨在寻求更适用于实际的漏失压力计算模型。
1 裂缝性地层漏失机理钻井过程中的裂缝性地层漏失通常发生于石灰岩、白云岩,或断层、地层不整合面、地层破碎带及火成岩等地层中,包括天然裂缝性漏失和诱导裂缝性漏失[9-11]。天然裂缝性漏失指地层本身存在许多的非致漏天然裂缝而导致漏失。天然裂缝分布和发育不均,形状可能为直线、曲线或波浪形,裂缝表面可能光滑或粗糙。在钻井液正压差的作用下,开度很小的天然裂缝逐渐扩展,直到扩展为致漏裂缝并与地层中其他裂缝连通,如果钻井液不能起到很好的封堵效果时,即转化为裂缝性漏失。诱导裂缝性漏失指地层本身并不存在天然裂缝,但由于地层强度低或含层理、节理等,在钻井液压力的作用下形成诱导裂缝,逐渐扩展并发生漏失。诱导裂缝通常有2种起因:一为外力大于地层破裂压力而引起诱导缝;二为外力引起地层闭合裂缝的再次开启。诱导缝主要为1条垂直张性缝,走向与最大主应力方向平行,并在两旁伴有2组高角度的共轭剪切缝。诱导性裂缝多发生在钻遇高压油气层、下钻速度快及井下长期未循环开泵过快等工况[12-16]。
2 裂缝性地层漏失压力模型 2.1 最小水平主应力漏失模型最小水平主应力漏失模型认为,对于含层理、节理和闭合裂缝的地层,钻井液沿着薄弱面侵入,使得裂缝张开的流体压力只需克服垂直裂缝面的地应力,即漏失压力近似为水平最小主应力。公式为:
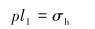
|
(1) |
式中:pl1为最小水平主应力模型确定的漏失压力,MPa;σh为水平最小主应力,MPa。
目前国内外有多种模型可求取水平最小主应力。国内常采用黄荣樽等建立的黄氏模型,其计算公式为:
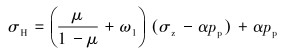
|
(2) |
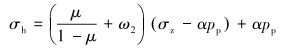
|
(3) |
式中:σH为水平最大主应力,MPa; ω1、ω2分别为水平构造应力系数;μ为泊松比;σz为上覆岩层压力,MPa;α为有效应力系数;pp为孔隙压力,MPa。
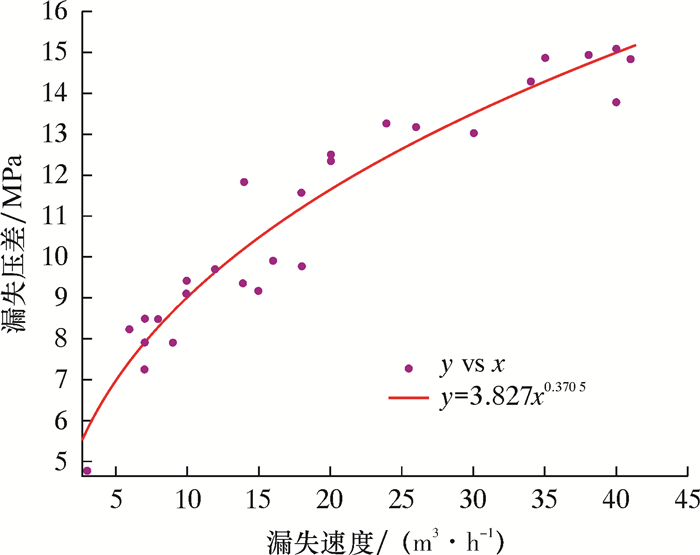
2.2 统计学漏失模型漏失压力的本质是地层发生漏失时的钻井液柱压力,而漏失压差则可定义为井内钻井液柱压力与地层孔隙压力的差值[17]。以渤中某区块裂缝性地层为例,基于现场实测漏失数据,从漏失压差的角度出发,漏失压差与漏失速度具有较好的关联性,如图 1所示。推广到一般意义上的裂缝性地层,可用该关联式描述漏失压差与漏失速度的关系,即有:
|
| 图 1 渤中某区块漏失压差与漏失速度关系图 Fig.1 The relationship between the leakage pressure difference and the leakage rate in Bozhong Block |
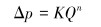
|
(4) |
式中:Q为漏失速率,m3/h;K为漏强系数;Δp为漏失压差,MPa;n为表征钻井液渗漏状态的系数,n=1时为中等孔隙度环境,n=2时为微孔隙环境。
因此,基于统计学的裂缝性地层漏失压力计算模型为:
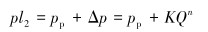
|
(5) |
式中:pl2为基于统计学的漏失压力,MPa。
2.3 临界裂缝宽度漏失模型国内外学者普遍认为,裂缝宽度影响裂缝性地层的敏感应力[18-20],继而影响漏失压力的大小。假设存在一临界裂缝宽度,当裂缝宽度小于临界裂缝宽度时,钻井液会在裂缝内形成具有一定承压能力的封堵层,钻井液正常滤失;当裂缝宽度超过临界裂缝宽度时,转化为裂缝性漏失。
裂缝变形符合幂函数形式,钻井液在裂缝中流动符合立方定律,裂缝宽度与有效应力的关系为:
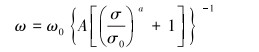
|
(6) |
式中:ω为裂缝动态宽度,mm;ω0为井筒压力等于地层压力时的裂缝宽度,mm;σ为垂直裂缝面的有效应力,MPa;σ0为井筒压力等于地层压力时垂直裂缝面的有效应力,MPa;A和a为待定系数。
以单条垂直缝为例,忽略井筒周围的应力集中,求得井筒液柱压力与裂缝面的有效正应力关系为:
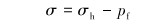
|
(7) |
式中:pf为井筒有效液柱压力,MPa。
联合式(6)和式(7),可得裂缝动态宽度与钻井液液柱压力的关系:
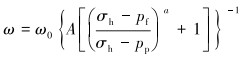
|
(8) |
从式(8)可看出,裂缝动态宽度与井筒液柱压力之间存在正相关关系。当裂缝宽度达临界裂缝宽度时,井下发生裂缝性漏失,基于临界裂缝宽度ωc的漏失压力计算模型为:
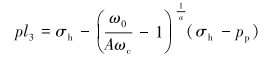
|
(9) |
式中:pl3为裂缝扩展压力,MPa。
2.4 裂缝圆环应力模型从岩石力学井壁围岩应力状态出发,认为井筒周围存在许多开度很小的天然裂缝。当裂缝发生扩展时,必然先从裂缝与井筒相交处进行,因此开展了裂缝与井眼相交处的应力状态研究,认为使得相交之处发生扩展的力为裂缝性地层漏失压力。考虑岩石为小变形弹性体、井壁围岩处于平面应变状态、符合线性叠加原理,得到斜井井壁围岩应力分布表达式为:
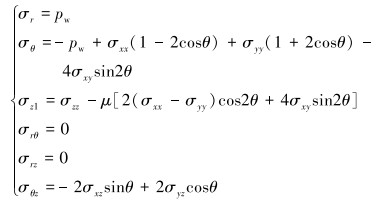
|
(10) |
式中:σr、σθ、σz1、σrθ、σrz和σθz为柱坐标中应力分量,MPa;pw为井内液柱压力,MPa;σxx、σyy、σxy、σzz、σxz和σyz为地应力分量,MPa;θ为地层中某点径向与水平最大主应力方向的夹角,(°)。
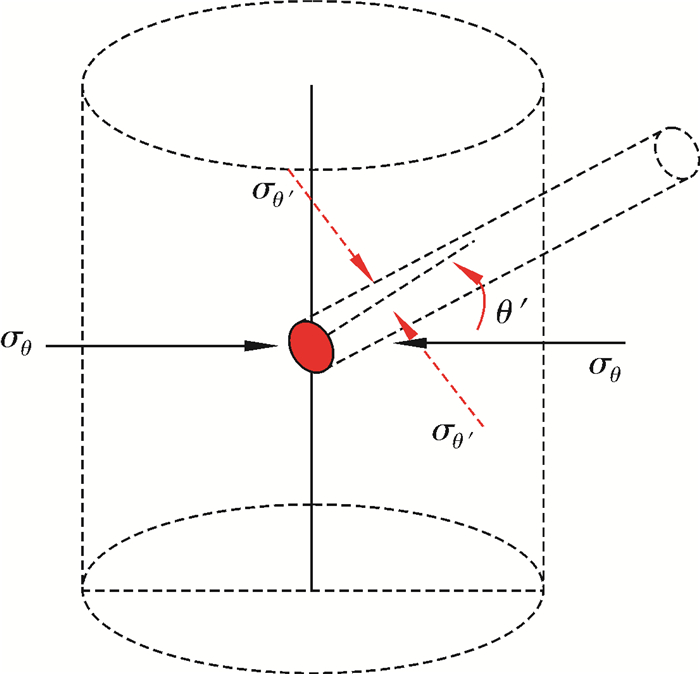
为简化计算模型,假设裂缝与井眼相交处为圆环面,从而建立裂缝性地层的裂缝圆环应力模型,θ′表示相交圆环面处任意一点与中心的连线和井壁围岩σθ方向的夹角,如图 2所示。对于裂缝与井筒相交圆环面,认为井壁上所受的应力为圆环面的远场地应力,按井壁围岩应力线性叠加原理求出圆环面上应力状态,分析井壁围岩各应力分量对裂缝与井筒圆环面应力的影响,可求得圆环面应力分布表达式为:
|
| 图 2 裂缝圆环应力模型 Fig.2 Fracture ring stress model |
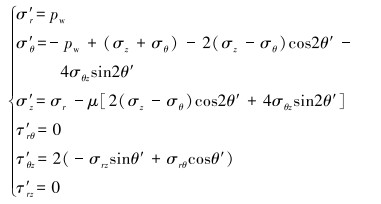
|
(11) |
式中:σ′r、σ′θ、σ′z、σ′rθ、σ′rz和σ′θz为裂缝圆环面上的6个应力分量,MPa。
借鉴破裂准则,认为裂缝性地层裂缝扩展时无需抵抗岩石的抗拉强度,即井壁上任一点处的最小主应力为0时,所求得的破裂压力即为裂缝扩展的压力,即σmin-αpp=0时得到的压力即为裂缝性地层漏失压力。
3 实例计算与分析渤中某区块漏失频发,漏失垂深在2 000~4 000 m,主要发生在硬脆性泥岩(灰质泥岩)、凝灰岩和玄武岩地层段,这些地层发育微小裂缝,为主要的漏失通道。结合漏失速度判定,认为该区块漏失属于裂缝性漏失。
渤中区块A井ϕ215.9 mm(8½in)井段3 234 m发生漏失,漏速40 m3/h,泵压16~19 MPa,排量1 800 L/min,钻井液密度1.44 g/cm3,钻井液塑性黏度30 mPa·s。结合漏失参数,可求得环空井段的紊流压耗、钻具内紊流压耗、地面管汇压耗及静液柱压力,继而求得漏失发生时的井底实际压力当量密度为1.467 g/cm3。
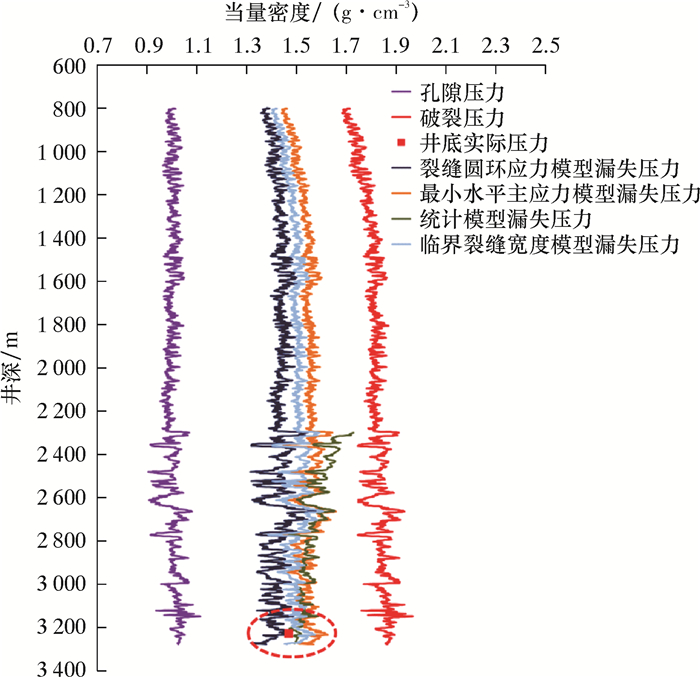
同时利用该井的钻井资料和测井资料等,根据前述4种计算模型对漏失压力进行实例计算,并与漏失点的实际井底压力进行了对比,结果如图 3所示。并将漏失点处各个模型计算得到的漏失压力与实际井底压力分别列出,如表 1所示。
|
| 图 3 渤中区块A井4种模型计算漏失压力与漏失点处井底实际压力对比图 Fig.3 Comparison of calculated loss pressure of Well A in Bozhong Block and the actual pressure at the bottom of the well |
| 漏失深度/m | 实际压力当量密度/(g·cm-3) | 最小水平主应力模型 | 统计模型 | 临界裂缝宽度模型 | 裂缝圆环应力模型 | |||||||
| 密度/ (g·cm-3) | 误差/% | 密度/ (g·cm-3) | 误差/% | 密度/ (g·cm-3) | 误差/% | 密度/ (g·cm-3) | 误差/% | |||||
| 3 234 | 1.467 | 1.570 | 7.0 | 1.497 | 2.0 | 1.522 | 3.7 | 1.412 | 符合 | |||
| 注:计算漏失压力小于井底实际压力时,符合现场实际情况。 | ||||||||||||
由图 3可知,就整个井深漏失压力剖面而言,存在趋势为裂缝圆环应力模型漏失压力<临界裂缝宽度模型漏失压力<统计模型漏失压力<最小水平主应力模型漏失压力。结合表 1中实际漏失点处各个模型的漏失压力与井底压力,最小水平主应力模型、统计模型和临界裂缝宽度模型计算结果均高于实际值,计算误差在2%~7%之间,不符合工程实际。裂缝圆环应力新模型计算得到的漏失压力小于实际井底压力,与另外3种模型对比,满足实际情况。最小水平主应力模型不适合裂缝发育地层,建议常规地层使用;统计模型和临界裂缝宽度模型需要已钻井资料支持,不适合探井及评价井的漏失压力计算。结合裂缝性漏失机理及可操作性分析,裂缝圆环应力模型可指导裂缝性地层钻井液密度设计。
4 结论与建议(1) 裂缝性地层漏失包括天然裂缝性漏失和诱导裂缝性漏失。在钻井液正压差的作用下,地层的天然裂缝或由于钻井液柱压力过大而产生的诱导裂缝逐渐扩展,直至与地层中其他裂缝互相连通,当钻井液封堵能力不足时,则会发生裂缝性漏失。
(2) 建立了4种裂缝性地层漏失压力模型,分别为最小水平主应力模型、基于统计学的漏失模型、基于临界裂缝宽度的漏失模型和基于裂缝圆环应力的漏失模型。不同模型出发点和考虑角度不同,经计算得到的漏失压力大小存在差异。
(3) 以渤中区块某裂缝性地层井为例,利用测井资料与钻井资料分别对4种模型进行了漏失压力剖面计算,并与实际漏失点处的井底压力进行了对比。分析结果表明:针对整个井深的漏失压力剖面,趋势为裂缝圆环应力模型漏失压力<临界裂缝宽度模型漏失压力<统计模型漏失压力<最小水平主应力模型漏失压力;针对实际漏失点,裂缝圆环应力模型求得的漏失压力值更符合现场实际。
(4) 漏失压力是地层漏失性质中的重要参数,目前研究仍处于起步阶段,建议进一步加深裂缝性地层漏失机理的认识,并加强漏失压力模型研究。
| [1] |
邓金根, 张洪生.
钻井工程中井壁失稳的力学机理[M]. 北京: 石油工业出版社, 1998.
DENG J G, ZHANG H S. Mechanical mechanism of borehole instability in drilling engineering[M]. Beijing: Petroleum Industry Press, 1998. |
| [2] |
朱荣东, 陈平, 夏宏泉, 等. 裂缝井壁力学稳定性研究[J].
断块油气田, 2007, 14(5): 56-58.
ZHU R D, CHEN P, XIA H Q, et al. Study on stability of fractured borehole wall[J]. Fault-Block Oil & Gas Field, 2007, 14(5): 56-58. DOI: 10.3969/j.issn.1005-8907.2007.05.020 |
| [3] | DAVIDSON E, RICHARDSON L, ZOLLER S. Control of lost circulation in fractured limestone reservoirs[R]. SPE 62734, 2000. |
| [4] |
王东明, 陈勉, 罗玉财, 等. 华北古近系及潜山内幕地层井壁稳定性研究[J].
钻井液与完井液, 2016, 33(6): 33-39.
WANG D M, CHEN M, LUO Y C, et al. Borehole stability in drilling the Paleogene System and inner buried hill in Huabei Oilfield[J]. Drilling Fluid & Completion Fluid, 2016, 33(6): 33-39. DOI: 10.3969/j.issn.1001-5620.2016.06.006 |
| [5] |
赵亚宁, 陈金霞, 卢淑芹, 等. 南堡中深层复杂岩性地层井壁失稳机理及技术对策[J].
钻井液与完井液, 2015, 32(5): 41-45.
ZHAO Y N, CHEN J X, LU S Q, et al. Borehole instability and countermeasures taken in drilling deep complex rock formations in Nanpu[J]. Drilling Fluid & Completion Fluid, 2015, 32(5): 41-45. |
| [6] | YU M, CHEN G, CHENEVERT M E, et al. Chemical and thermal effects on wellbore stability of shale formations[R]. SPE 71366, 2001. |
| [7] |
朱亮, 张春阳, 楼一珊, 等. 两种漏失压力计算模型的比较分析[J].
天然气工业, 2008, 28(12): 60-61, 67.
ZHU L, ZHANG C Y, LOU Y S, et al. Comparative analysis between the mechanics-based and statistics-bused calculation models for leakage pressure[J]. Natural Gas Industry, 2008, 28(12): 60-61, 67. DOI: 10.3787/j.issn.1000-0976.2008.12.016 |
| [8] |
李双贵, 易浩, 张俊, 等. 麦盖提1区碳酸盐岩地层钻井漏失分析及优化[J].
石油天然气学报, 2012, 34(9): 109-112.
LI S G, YI H, ZHANG J, et al. Lost circulation analysis and optimization of drilling fluids in carbonate reservoir of block Maikit 1[J]. Journal of Oil and Gas Technology, 2012, 34(9): 109-112. DOI: 10.3969/j.issn.1000-9752.2012.09.023 |
| [9] |
金衍, 齐自立, 陈勉, 等. 水平井试油过程裂缝性储层失稳机理[J].
石油学报, 2011, 32(2): 295-298.
JIN Y, QI Z L, CHEN M, et al. A mechanism study on the fractured reservoir instability during well testing of horizontal wells[J]. Acta Petrolei Sinica, 2011, 32(2): 295-298. |
| [10] | ALTINDAG R. Assessment of some brittleness indexes in rock-drilling efficiency[J]. Rock Mechanics and Rock Engineering, 2010, 43(3): 361-370. DOI: 10.1007/s00603-009-0057-x |
| [11] |
周健, 陈勉, 金衍, 等. 裂缝性储层水力裂缝扩展机理试验研究[J].
石油学报, 2007, 28(5): 109-113.
ZHOU J, CHEN M, JIN Y, et al. Experimental study on propagation mechanism of hydraulic fracture in naturally fractured reservoir[J]. Acta Petrolei Sinica, 2007, 28(5): 109-113. DOI: 10.3321/j.issn:0253-2697.2007.05.020 |
| [12] |
贾利春, 陈勉, 侯冰, 等. 裂缝性地层钻井液漏失模型及漏失规律[J].
石油勘探与开发, 2014, 41(1): 95-101.
JIA L C, CHEN M, HOU B, et al. Drilling fluid loss model and loss dynamic behavior in fractured formations[J]. Petroleum exploration and development, 2014, 41(1): 95-101. |
| [13] | AADNOY B S, BELAYNEH M, JORQUERA M A A, et al. Design of well barriers to combat circulation losses[R]. SPE 105449, 2008. |
| [14] | ZHANG F X, ZHANG S L, JIANG X H, et al. Borehole stability in naturally fractured reservoirs during production tests[J]. Petroleum Science, 2008, 5(3): 247-250. DOI: 10.1007/s12182-008-0039-8 |
| [15] |
舒刚, 孟英锋, 李红涛, 等. 裂缝内钻井液的漏失规律研究[J].
石油钻采工艺, 2011, 32(6): 29-32.
SHU G, MENG Y F, LI H T, et al. Leakage laws research of drilling fluid in fracture reservoir[J]. Oil Drilling & Production Technology, 2011, 32(6): 29-32. DOI: 10.3969/j.issn.1000-7393.2011.06.007 |
| [16] |
赵凯, 樊勇杰, 于波, 等. 硬脆性泥页岩井壁稳定研究进展[J].
石油钻采工艺, 2016, 38(3): 277-285.
ZHAO K, FAN Y J, YU B, et al. Research progress of wellbore stability in hard brittle shale[J]. Oil Drilling & Production Technology, 2016, 38(3): 277-285. |
| [17] |
金衍, 陈勉, 刘晓明, 等. 塔中奥陶系碳酸盐岩地层漏失压力统计分析[J].
石油钻采工艺, 2007, 29(5): 82-84.
JIN Y, CHEN M, LIU X M, et al. Statistic analysis of leakage pressure of Ordovician carbonate formation in middle Tarim Basin[J]. Oil Drilling & Production Technology, 2007, 29(5): 82-84. DOI: 10.3969/j.issn.1000-7393.2007.05.023 |
| [18] |
李大奇. 裂缝性地层钻井液漏失动力学研究[D]. 成都: 西南石油大学, 2012. LI D Q. Numerical and experimental investigations of drilling fluid losses in fractured formations[D]. Chengdu: Southwest Petroleum University, 2012. |
| [19] |
李大奇, 康毅力, 刘修善, 等. 基于漏失机理的碳酸盐岩地层漏失压力模型[J].
石油学报, 2011, 32(5): 900-904.
LI D Q, KANG Y L, LIU X S, et al. The lost circulation pressure of carbonate formations on the basis of leakage mechanisms[J]. Acta Petrolei Sinica, 2011, 32(5): 900-904. |
| [20] | CATALIN I, JAMES B, BEN B. Lost circulation can be managed better than ever[J]. World Oil, 2003, 224(6): 35-41. |



