2. 长江大学机械工程学院
2. School of Mechanical Engineering, Yangtze University
0 引言
管柱的失稳常由轴向载荷、扭矩、与井眼内壁的摩擦及其自重等因素引起,另外井眼中可能还有流体、温度和压力等因素需要考虑,因此屈曲问题异常复杂[1]。目前,已有不少学者对连续管做了大量研究,相关理论研究已经比较完善,但是关于连续管屈曲方面的试验研究还很少,而且大部分只是对理论模型的验证或者试验效果不太好,未能达到理想的效果,无法真实地反映真实管线中管柱的力学行为[2-6]。长江大学的管锋和马卫国等[7-9]开发出一套含水平井、弯曲井在内的全井段连续管井下力学行为模拟试验系统,更全面地开展了试验研究,有助于了解连续管在井筒内的力学行为等,同时对生产现场和实际入井操作有一定的指导意义。
笔者在文献[7-9]试验数据和试验现象的基础上,得到了符合工程实际的全管段轴力传递模型,然后根据得到的轴力传递模型,进行了实际连续管下入深度的计算分析。
在试验中通过观察,每次试验均出现正弦屈曲和螺旋屈曲,弯管段基本不出现螺旋屈曲。笔者根据试验现象,在钢丝末端非自由螺旋屈曲轴力传递分析时引进较合适的接触力系数,具有一定的说服力。另外,经过试验验证发现,管柱屈曲只与其自身刚度有关,而与管柱是否空心无关,在假设实际管线中的流体和管内温度可忽略时,实际连续管和试验中的钢丝有着相同的工作环境,因此试验中的钢丝模型也适用于实际连续管状况,进而通过试验得出轴力传递模型可以用于实际连续管在管线中的下放计算的结论。
1 管柱轴力传递分析 1.1 实际管线各段中管柱屈曲分析文献[7]的试验受试验场地限制,未能模拟竖直段-弯曲段-水平段的全管段试验,但是考虑到试验中钢丝重力可以忽略不计,因此可以将其近似看成竖直段-弯曲段-水平段的全管段模拟试验,与常见的管线结构类似。
当连续管开始形成正弦或螺旋屈曲之前,处于轴向压缩的连续管被推向弯曲管线的外侧,而弯管段的临界屈曲载荷较大,一般轴力较大才会发生正弦屈曲[10]。竖直段的螺旋屈曲临界载荷较小,容易发生螺旋屈曲,水平段的屈曲载荷大于竖直段的屈曲载荷,因此竖直段一般发生螺旋屈曲。
图 1所示为竖直段和水平段均发生螺旋屈曲的模型示意图。
|
| 图 1 管柱在竖直和水平直管段发生螺旋屈曲 Fig.1 Helical buckling of the coiled tubing in vertical and lateral sections |
1.2 竖直段轴力传递
目前关于竖直段的轴力计算的理论已经非常成熟,竖直井中管柱屈曲临界载荷Fcrh为[11]:

|
(1) |
式中:EI为连续管刚度,N·m2;q为连续管在井筒介质中单位长度重力,N/m;γ为无量纲系数,对于正弦屈曲临界载荷,该系数取2.55,对于螺旋屈曲临界载荷,该系数取5.55。
试验中,处于竖直段的钢丝发生螺旋屈曲,R.F.MITCHELL[12]给出螺旋屈曲时的接触力N为:
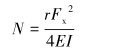
|
(2) |
式中:r为管柱和井筒之间的径向间隙,m;Fx为轴力,N。
嵇国华[13]用微元法计算竖直段发生螺旋屈曲并且考虑重力的轴力传递公式为:
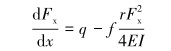
|
(3) |
使用微元法有:
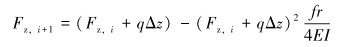
|
(4) |
式中:Δz为微元段长度,m;f为连续管与井筒内壁之间的摩擦因数;Fz, i为单元体(i=0, 1, 2……)首端压力,N;Fz, i+1为所取单元体(i=0, 1, 2……)末端压力,N。
1.3 弯管段正弦屈曲轴力传递模型实际作业时虽然弯曲段基本不发生正弦屈曲,但是通过文献[7]中的试验发现,每次试验中弯管段均出现正弦屈曲。正弦屈曲模型中的角位移θ、正弦曲线长度p分别由式(5)和式(6)给出[2, 4]。
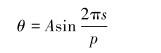
|
(5) |
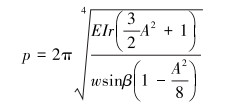
|
(6) |
轴力Fx、接触力Nc与正弦屈曲幅值A的关系分别由式(7)和式(8)给出[2, 4]。
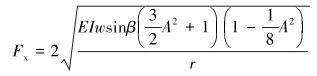
|
(7) |
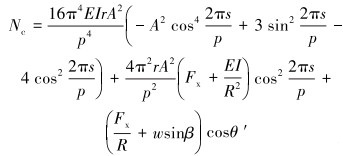
|
(8) |
式中:β为井斜角,rad;θ′为弯管中管柱与水平方向的夹角,rad;w为单位管段线重力,N/m;s为沿井筒中心线管柱的长度,m;R为弯管半径,m;A为管柱在弯管井筒中正弦屈曲的幅值,rad。
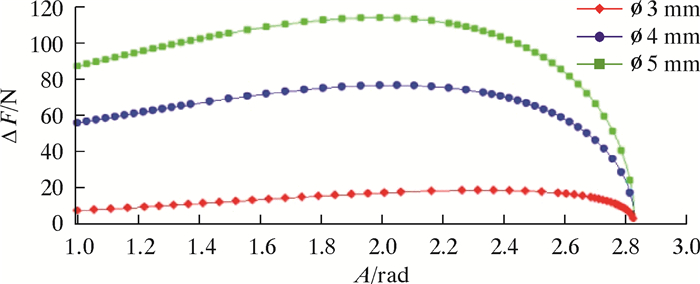
由式(6)、式(7)和式(8)可知,正弦曲线长度p为正弦曲线幅值A的函数,角位移θ和轴向压力Fx是A和井斜角β的函数,将式(5)、式(6)和式(7)代入式(8),可得接触力Nc的表达式。由式(7)可得幅值A小于2.9,将弯曲段按照井斜角无限细分,迭加得到每一小段的接触力,根据接触力与轴力的关系,得到由于与弯管内壁面接触力Nc引起的轴力减少量ΔF随幅值A的变化关系图,如图 2所示。
|
| 图 2 3种钢丝弯管轴力减少量随A的变化 Fig.2 The effect of A on axial force reduction of the three kinds of bending steel wire |
试验中3种钢丝均发生了螺旋锁死,由此可知各点轴向力较大,因此弯曲段的接触力也应该较大。由图 2可知,当A取2时,弯曲段的接触力最大,符合实际情况。A确定后,接触力关于井斜角β的关系可由式(8)确定。
对式(8)进行拟合,得出接触力关于井斜角β的几何表达式:
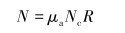
|
(9) |
然后由
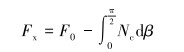
|
(10) |
式中:F0为首端压力。
2 接触力修正系数分析根据查阅的资料来看,螺旋屈曲接触力在理论计算中常采用末端自由的情况,R.F.MITCHELL等多位学者通过多种方法基本上得出了相同的公式形式。但是在试验中由于末端并非自由的形式,而是固定、移动负载的形式,那么这种情况下的螺旋屈曲接触力需要对式(2)进行修正,变为:
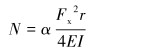
|
(11) |
此前也有学者研究过末端非自由时引进螺旋屈曲接触力修正系数α,但是不同的学者得到的修正系数值不同。K.G.SORENSON等[14]认为管端有约束和不考虑自重的影响时,接触压力的分布会受到约束的影响。张永弘等[15]假设管柱为无限长、无自重而且是管端无约束,推导得到修正系数α为0.25。R.DAWSON[16]认为, 不考虑自重时,α为0.5。
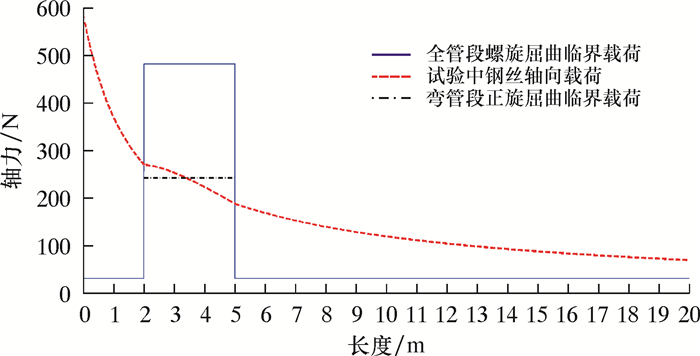
下面将根据试验现象和试验数据仔细探讨末端非自由时需要引进的接触力修正系数。试验中3种钢丝在弯管段均发生了正弦屈曲,据此画出的轴力图和正弦屈曲临界载荷图中,弯管段轴力图应该在正弦屈曲临界载荷图上方。图 3为ϕ4 mm钢丝在第1直管段螺旋屈曲时的轴力分布图。
|
| 图 3 ϕ4 mm钢丝不引入接触力修正系数轴力图 Fig.3 The axial force of the ϕ4 mm steel wire without contact force correction coefficient |
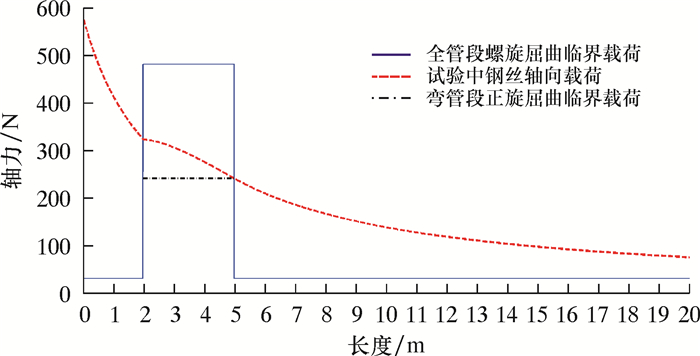
由图 3可以看出,在3 m弯管段,轴力线部分已经位于正弦屈曲临界载荷之下了,明显与实际情况不合。图 4是ϕ4 mm钢丝在引进α后的临界情况。
|
| 图 4 ϕ4 mm钢丝引入接触力修正系数后轴力图 Fig.4 The critical axial force of the ϕ4 mm steel wire with contact force correction coefficient |
由于ϕ3 mm钢丝很容易锁死,所以首端压力没能加到很大,导致需要引进较小的螺旋屈曲接触力系数才能使其在弯管段的轴力曲线均在其对应的正弦屈曲临界载荷曲线之上,而直径为4和5 mm的钢丝需要引进的系数则较大。为使三者形成对比,假设3种钢丝在前2 m轴力相对减少系数相同,表 1为直径d=3、4和5 mm等3种钢丝在第1直管段内相应的螺旋屈曲接触力修正系数α取值。
| d/mm | 3 | 4 | 5 |
| α | 0.273 9 | 0.590 0 | 0.627 7 |
在确定了第1直管段的接触力系数后,由前面的轴力传递公式可得d=3、4和5 mm时3种钢丝在第2直管段的首端压力,并根据15 m直管段末端压力值得到第2直管段的螺旋屈曲接触力修正系数,结果见表 2。
| d/mm | F0/N | Fb′/N | F0′/N | Fb/N | α′ |
| 3 | 135.75 | 110.20 | 75.00 | 17.60 | 0.896 |
| 4 | 583.53 | 457.60 | 375.00 | 81.00 | 0.654 |
| 5 | 1 266.40 | 1 014.50 | 851.00 | 225.00 | 0.559 |
| 注:其中Fb为末端压力,Fb′为第1直管段末端压力,F0′为第2直管段首端压力,α′为第2直管段修正系数。 | |||||
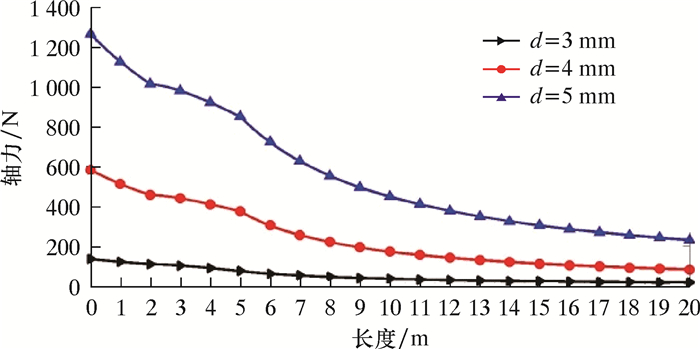
图 5是d=3、4和5 mm的3种钢丝在20 m全管段的轴力传递曲线。
|
| 图 5 3种钢丝全管段轴力分布 Fig.5 Axial force distribution of the three kinds of steel wire |
从图 5可以发现,在引进接触力修正系数后,3种钢丝轴力呈持续下降趋势,在第1直管段轴力减小速率较大,第2直管段轴力减小比较平缓。造成这种现象主要是钢丝在第1直管段和第2直管段均发生螺旋屈曲,二者不同之处在于第1直管段内钢丝末端为自由状态,而第2直管段末端固定,而末端固定时轴力较难传递,因此轴力减小速率较小。
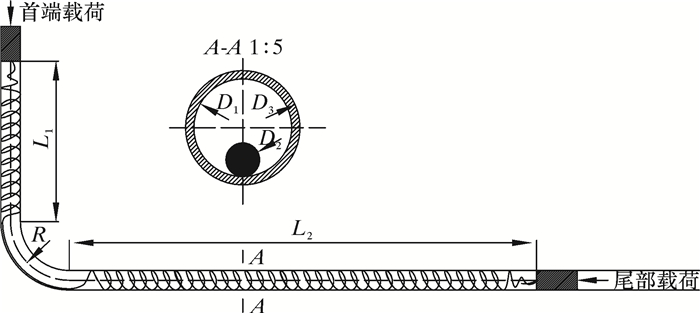
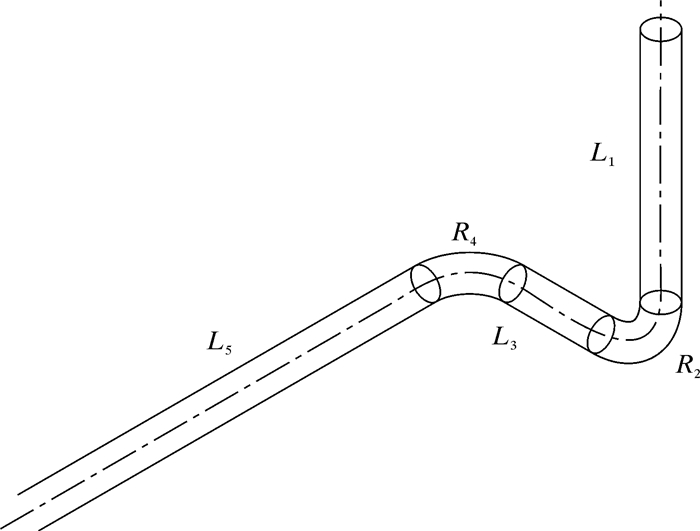
3 实际管柱下入特性分析 3.1 基本原始数据该部分针对实际连续管在首端注入力为225 kN时的下放特性进行分析,即连续管下放时在末端轴力为0,为终止条件下能够下放的最大深度。管柱为竖直井→弯管井→水平井→弯管井→水平井的结构,管柱结构示意图如图 6所示。为简化分析,没有考虑管柱方位角的影响。
|
| 图 6 管柱结构示意图 Fig.6 Coiled tubing structure |
| 参数 | L1 | R2 | L3 | R4 | L5 |
| 尺寸/m | 75.280 | 1.525 | 26.540 | 1.525 | 3 900 |
3.2 南海油田实例
实际连续管通过自身重力和首端施加注入力作用下放到预定的位置进行作业。实际下放时,连续管的总重力、与管壁的摩擦力以及首端注入力会不断变化,是一个动态过程。笔者在首端注入力稳定的情况下分析连续管的下放,在分析中没有考虑部分管柱因首端受压力扭矩过大或者下放受阻发生锁死而无法行进的情况。表 4为不同工况下连续管在南海油田的下放特性。其中:工况1为连续管外径D1=44.5 mm,D2=37.6 mm,r=0.130 m,EI=19 550 N·m2,q=3.45 N/m;工况2为D1=50.8 mm,D2=44.0 mm,r=0.127 m,EI=300 49 N·m2,q=3.98 N/m;工况3为D1=60.3 mm,D2=52.4 mm,r=0.122 m,EI=58 690 N·m2,q=5.50 N/m;工况4为D1=73.0 mm,D2=64.1 mm,r=0.116 m,EI=118 710 N·m2,q=7.52 N/m;工况5为D1=88.9 mm,内径D2=80.0 mm,r=0.108 m,EI=221 637 N·m2,q=9.27 N/m。
| 工况 | 不同摩擦因数下的下入深度/m | ||||
| f=0.10 | f=0.15 | f=0.20 | f=0.25 | f=0.30 | |
| 工况1 | 4 584 | 3 078 | 2 320 | 1 861 | 1 529 |
| 工况2 | 5 218 | 3 512 | 2 650 | 2 129 | 1 741 |
| 工况3 | 6 109 | 4 119 | 3 113 | 2 505 | 2 039 |
| 工况4 | 7 329 | 4 935 | 3 731 | 3 004 | 2 446 |
| 工况5 | 8 889 | 5 969 | 4 505 | 3 624 | 3 033 |
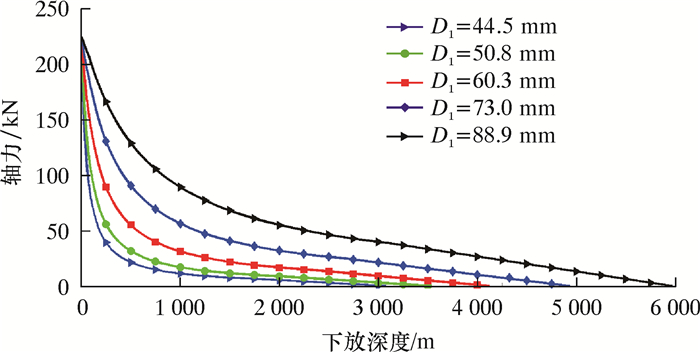
为比较连续管尺寸对下放深度的影响,笔者从中挑选出了5种不同连续管在相同摩擦因数(μ=0.15)下的下放特性,结果如图 7所示。
|
| 图 7 5种尺寸连续管的下放特性 Fig.7 Running behaviors of five sizes of coiled tubing |
从图 7可以看出,5种尺寸的连续管在相同的摩擦因数下,下放深度随管径增大而增大,ϕ88.9 mm的管柱刚度较大,不易发生屈曲,因此下放的深度最深。理论情况下ϕ44.5 mm的连续管在f=0.15时最大下放深度为3 078 m,ϕ88.9 mm的连续管在f=0.15时下放深度为5 969 m,后者管径差不多为前者的2倍,下放深度也差不多为前者的2倍。从表 3可知,井眼全部5段中心线总长度只有4 004 m,所以只有ϕ60.3、ϕ73.0和ϕ88.9 mm的连续管在井眼中可以完全下放,另外2种尺寸的连续管则只能下放一部分。
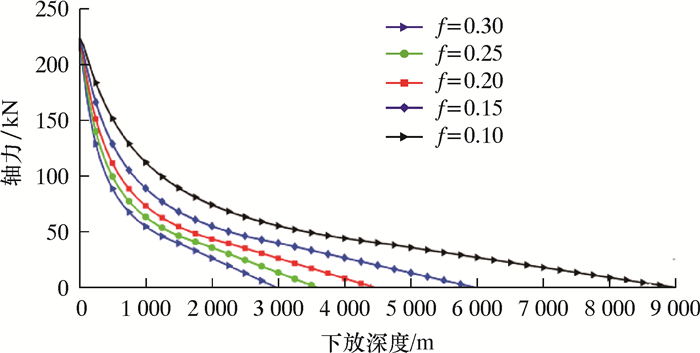
另外,为比较摩擦因数f对下放深度的影响,笔者选择了管径为88.9 mm的连续管在5种不同的摩擦因数下的下放特性,结果如图 8所示。
|
| 图 8 连续管在5种摩擦因数下的下放特性 Fig.8 Running behaviors of the coiled tubing under five friction factors |
从图 8可以看出,ϕ88.9 mm的连续管下放深度随摩擦因数增大而减小,在f=0.10时可以下放9 000 m左右,而f=0.30时则只能下放3 000 m左右,其他尺寸的连续管具有相同的规律。值得注意的是,连续管下放的深度和摩擦因数并非线性相关,对ϕ88.9 mm的连续管而言,能够在摩擦因数为0.10、0.15和0.20时完全下放,在其余2种摩擦因数下则只能下放一部分。
4 结论(1) 分析了实际管柱在各段发生屈曲的可能形式,用迭代的方法得到了试验中的钢丝在弯管段发生正弦屈曲时轴力传递情况,在考虑其重力的情况下,用微元法得到了管柱在竖直段发生螺旋屈曲时轴力的传递公式。
(2) 基于试验现象和试验数据,确定了不同钢丝在末端非自由时需要引进的螺旋屈曲接触力修正系数。
(3) 分析管径和管道摩擦因数对连续管下放特性的影响时发现,管径越大,下放深度越大,摩擦因数越大,下放深度越小。另外,通过对比分析发现,不同连续管在与管柱内壁相同摩擦因数时有部分连续管不能完全下放,如摩擦因数为0.15时只有ϕ60.3、ϕ73.0和ϕ88.9 mm的连续管在管线中可以完全下放。同种连续管在与管柱内壁不同摩擦因数时有部分情况也不能完全下放,如ϕ88.9 mm的连续管只有在摩擦因数为0.10、0.15和0.20时可以完全下放。
| [1] |
陈迎春, 张仕民, 王文明, 等. 连续油管屈曲力学特性研究进展[J].
石油矿场机械, 2013, 42(12): 15-20.
CHEN Y C, ZHANG S M, WANG W M, et al. Study progress in buckling behavior of coiled tubing[J]. Oil Field Equipment, 2013, 42(12): 15-20. DOI: 10.3969/j.issn.1001-3482.2013.12.004 |
| [2] | MISKA S, QIU W Y, VOLK L, et al. An improved analysis of axial force along coiled tubing in inclined/horizontal wellbores international conference on horizontal well technology[R]. SPE-37056-MS, 1996. |
| [3] | QIU W. Theoretical and experimental study of buckling behavior of coiled tubing and axial force transfer modeling in coiled tubing drilling[D]. Tulsa: The University of Tulsa, 1997. |
| [4] | KURU E, MARTINEZ A, MISKA S, et al. The buckling behavior of pipes and its influence on the axial force transfer in directional wells[R]. SPE-52840-MS, 1999. |
| [5] | MENAND S, SELLAMI H, TIJANI M, et al. Buckling of tubulars in simulated field conditions[J]. SPE Drilling & Completion, 2009, 24(2): 276-285. |
| [6] |
焦朝选, 李茂生, 张钒, 等. 涡动条件下钻柱的屈曲分析[J].
石油机械, 2011, 39(5): 1-4.
JIAO C X, LI M S, ZHANG F, et al. A buckling analysis of the drillpipe in the condition of whirling[J]. China Petroleum Machinery, 2011, 39(5): 1-4. |
| [7] |
管锋, 段梦兰, 马卫国, 等. 连续油管井下力学行为模拟实验研究[J].
力学与实践, 2012, 34(5): 21-26, 56.
GUAN F, DUAN M L, MA W G, et al. The experimental simulation of mechanical behavior of coiled tubing in wells[J]. Mechanics in Engineering, 2012, 34(5): 21-26, 56. |
| [8] |
马卫国, 管锋, 斯拉英·库尔班库尔班, 等. 连续管在水平井井筒中的力学模拟试验系统[J].
石油机械, 2012, 40(11): 79-82.
MA W G, GUAN F, SILAYING K E B, et al. Mechanical simulation test for CT in the horizontal well[J]. China Petroleum Machinery, 2012, 40(11): 79-82. |
| [9] | GUAN F, DUAN M L, MA W G, et al. An experimental study of mechanical behavior of coiled tubing in pipelines[J]. Applied Ocean Research, 2014, 44: 13-19. DOI: 10.1016/j.apor.2013.10.009 |
| [10] | HE X J, KYLLINGSTAD A. Helical buckling and lock-up conditions for coiled tubing in curved wells[J]. SPE Drilling & Completion, 1995, 10(1): 10-15. |
| [11] | WU J, JUVKAM-WOLD H C. Coiled tubing buckling implication in drilling and completing horizontal wells[J]. SPE Drilling & Completion, 1995, 10(1): 16-21. |
| [12] | MITCHELL R F. Simple frictional analysis of helical buckling of tubing[J]. SPE Drilling Engineering, 1986, 1(6): 457-465. |
| [13] |
嵇国华. 直井管柱屈曲对轴力传递的影响[J].
油气井测试, 2009, 18(5): 11-12, 16.
JI G H. The buckling behavior of pipe string and its influence on the axial force transfer in vertical wells[J]. Well Testing, 2009, 18(5): 11-12, 16. DOI: 10.3969/j.issn.1004-4388.2009.05.003 |
| [14] | SORENSON K G, CHEATHAM J B. Post-buckling behavior of a circular rod constrained within a circular cylinder[J]. Journal of Applied Mechanics, 1986, 53(4): 929-934. DOI: 10.1115/1.3171883 |
| [15] |
张永弘, 刘恩, 何富君, 等. 管柱螺旋屈曲时接触压力的研究[J].
石油学报, 1998, 19(3): 131-134.
ZHANG Y H, LIU E, HE F J, et al. A study of contact forces on helical buckled tubing in wells[J]. Acta Petrolei Sinica, 1998, 19(3): 131-134. |
| [16] | DAWSON R, PASLAY P R. Drillpipe buckling in inclined holes[J]. Journal of Petroleum Technology, 1984, 36(11): 1734-1738. |




