2. 中国石油大学(北京)机械与储运工程学院;
3. 中国石油大学(北京)海洋工程研究院
2. College of Mechanical and Transportation Engineering, China University of Petroleum(Beijing);
3. Offshore Engineering Research Institute, China University of Petroleum(Beijing)
0 引言
柔性立管在保证较大轴向刚度的同时还可以承受很大的弯曲变形,它作为海上浮体与井口连接的通道,得到了越来越广泛的应用。作为海上油气运输的柔性立管,其一旦失效将会对海洋环境造成巨大的危害,并且对整个海上油气生产系统带来巨大的经济损失。我国在海洋油气资源开发方面起步晚、起点低,对此类立管的设计和建造经验明显不足,不得不依托国外公司。另一方面,近几十年来国际学术界和工业界对非黏结柔性立管的研究兴趣有增无减,从最初的简化模型到能更真实地反映其特性的复杂模型,从截面力学性能分析到典型失效特性分析,都开展了较详细和深入的研究。对于柔性立管内部骨架层的失效形式,国内研究相对匮乏。因此,掌握骨架层失效机理,分析造成骨架失效的主要原因及影响因素对我国海洋油气资源开发关键技术具有重要的作用。
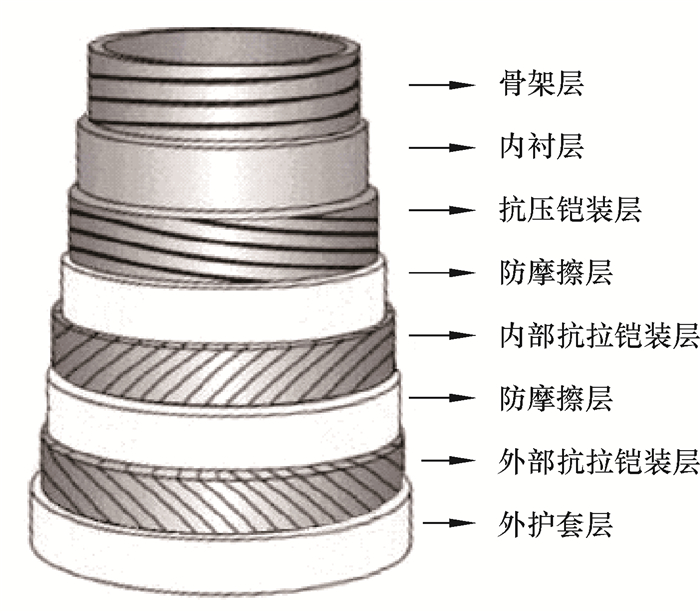
1 非黏结柔性立管及骨架层介绍非黏结柔性立管(见图 1)不通过特殊工艺处理,而是将各层按照一定顺序进行装配,相邻层间无黏结甚至存在缝隙,在外载荷作用下相邻层会根据载荷类型、方向和边界条件等自动调整层间相互接触或分离情况。相对于黏结柔性立管,非黏结柔性立管截面力学性能尤为复杂,对非黏结柔性立管特性研究一直是国际海洋工程领域的研究热点和难点。骨架层由截面近似S形不锈钢螺旋缠绕形成互锁型结构,如图 2所示。骨架层作为非黏结柔性立管最内层结构,其主要作用是承担外部传递来的径向压力[1]。在工程实践中,骨架层主要失效方式为径向压溃失效与轴向撕裂失效,笔者从理论模型与国内外研究进展对2种失效方式分别进行阐述。
|
| 图 1 非黏结柔性立管主要结构 Fig.1 Main structure of non-bonded flexible riser |

|
| 图 2 骨架层剖面结构 Fig.2 Profile of the carcass layer |
2 骨架层径向压溃失效
骨架层作为非黏结柔性立管的最内层结构,其主要作用是承担来自外部的径向压力。非黏结柔性立管骨架层压溃失效如图 3所示。导致其失效的载荷为均匀外压和径向压缩载荷等,其中径向压缩载荷主要来自铺管过程中张紧器等作用。径向失效是由于外部过大压力引起骨架层压溃失效,目前研究以理论与数值模拟相结合的方法,并进行试验验证。理论方法在求解骨架层失效特性时主要依据弹性稳定性理论[2],首先将截面形式复杂的骨架层等效为矩形截面圆环结构,然后根据圆环挠曲线微分方程求解均匀外压下临界压溃值和对径压缩载荷下径向位移。由于理论方法无法考虑骨架层初始缺陷、材料非线性和层间接触摩擦,所以可借助有限元软件进行数值模拟,并通过试验进行验证。

|
| 图 3 骨架层压溃失效 Fig.3 Collapse failure of the carcass layer |
2.1 骨架层圆环模型
目前关于骨架层径向失效理论模型主要基于铁木辛柯弹性理论中圆弧细杆的挠曲线微分方程[2],该理论模型假设径向存在较小的径向位移ω,忽略切向位移,其基本方程如下:
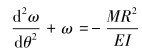
|
(1) |
式中:R为圆环半径,mm;EI为弯曲刚度;θ为偏转角度,rad;M为弯矩,N·mm。
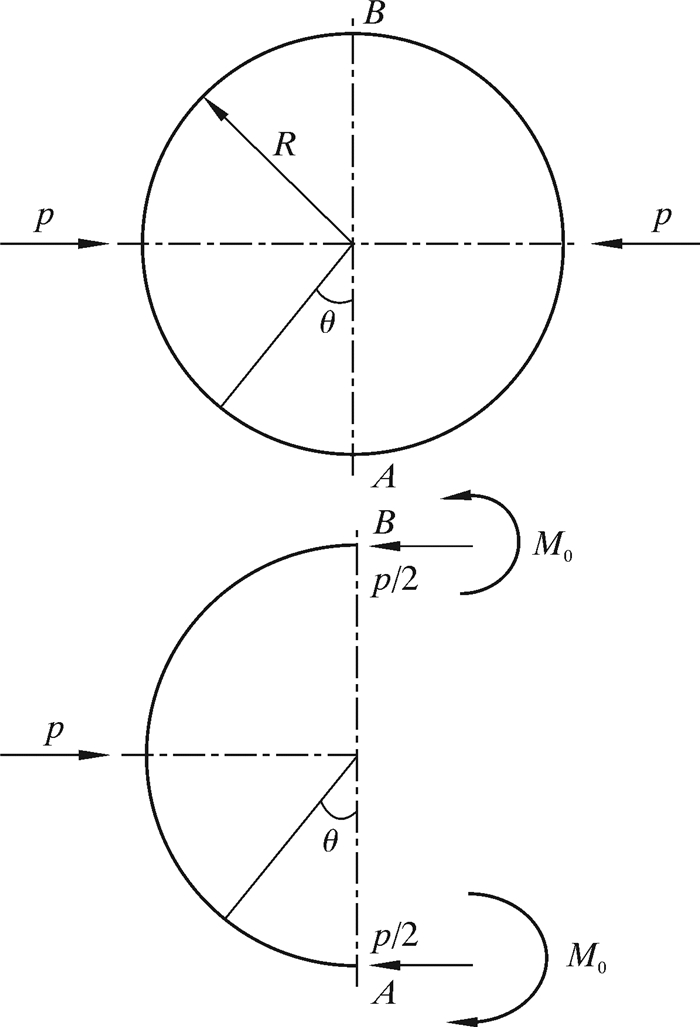
对称径向压力作用下圆环受力如图 4所示。
|
| 图 4 圆环受径向压力示意图 Fig.4 Schematic diagram of the ring under radial pressure |
当圆环受径向压力p时,圆环半径为R,A、B 2点弯矩为M0,此时圆环任何截面的弯矩可以表示为:
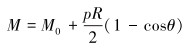
|
(2) |
将该方程代入挠曲线微分方程可得:
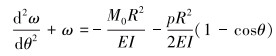
|
(3) |
其通解为:
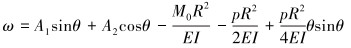
|
(4) |
根据对称边界条件,在θ=0和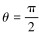
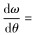
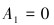
|
(5) |
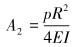
|
(6) |
对式(2)进行积分可得:
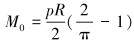
|
(7) |
将式(5)、式(6)和式(7)代入式(4)可求任意横截面处径向位移:
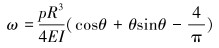
|
(8) |
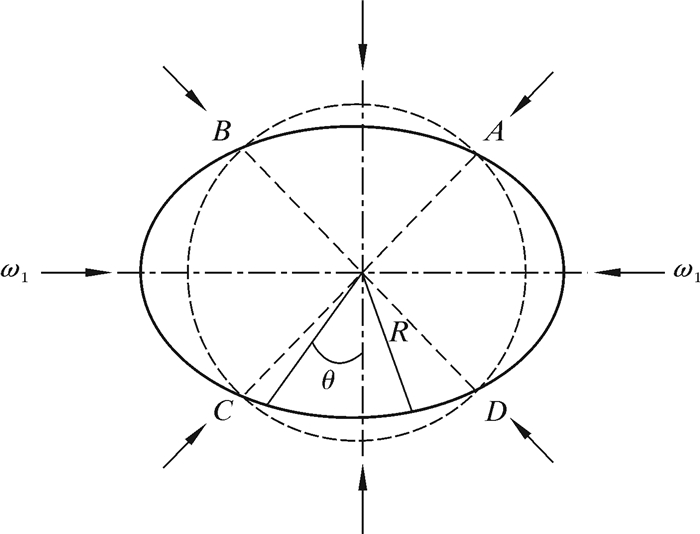
引入具有曲率的细杆挠曲线微分方程,研究具有初始径向位移ω1、圆环受均布外压q的弹性失效问题。如图 5所示,该圆环存在最大径向位移ω1,小变形下圆环任意界面初始位移为ωi=ω1cos2θ,此时任意截面的挠曲线微分方程可表示为:
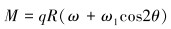
|
(9) |
|
| 图 5 圆环受均布外压示意图 Fig.5 Schematic diagram of uniform pressure distribution on the ring |
将式(9)代入式(1)可得:
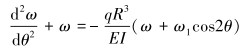
|
(10) |
根据A、B、C、D4点处的连续条件,可求得任意截面处位移:
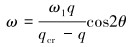
|
(11) |
qcr为临界压溃值,其解析表达式为:
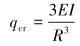
|
(12) |
为了使用铁木辛柯弹性理论模型,可借助C.A.MARTINS等[3]的等效厚度法去处理骨架层复杂的截面形状。为了计算等效厚度,一般使单位长度内骨架层的弯曲刚度相等,则等效厚度的表达式为:
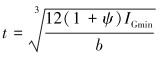
|
(13) |
式中:IGmin为骨架层剖面最小惯性矩,b为骨架层剖面长度。
ψ主要由骨架层轮廓形状与骨架层节距决定(主要考虑到骨架层轮廓重叠作用)。单位长度骨架层弯曲刚度越小,ψ就越准确。通过这种方法,计算ψ就是求轮廓之间重叠长度L与骨架层节距L′的比值,即到:
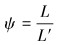
|
(14) |
A.G.NETO等[4]建立了真实螺旋缠绕骨架层与不考虑铺设角度的圆环骨架层模型,根据铁木辛柯弹性理论建立了圆环挠曲线微分方程进行求解。计算结果显示2种有限元模型数据吻合,理论模型与数值模拟结果存在差距。这说明对骨架层进行径向压溃研究时其铺设角度对数值结果影响较小,由于实际骨架层截面复杂,相邻表面会发生接触作用,所以简化的理论模型与实际结果之间存在一定的差距。
C.P.PESCE等[5]采用理论分析、数值模拟与试验相结合的方法对骨架层压溃进行研究分析。分别对ø60.1和ø101.6 mm的骨架层进行压力试验并求得其临界压溃值。运用数值模拟方法建立实际骨架层模型,并与试验结论进行比较,得到骨架层临界屈曲压溃值,运用得到的结果调整由理论模型求得的临界应力表达式,使三者得到较好的结合。
H.E.M.MERINO等[6]对柔性管道在外压和扭转共同作用下的情况进行数值模拟及试验研究,并将每个工况下的结果进行对比,结果显示扭转载荷对柔性管的压溃几乎没有影响,两者共同作用下的结果与只受外压载荷作用下的结果几乎相等。
V.P.P.NOGUEIRA等[7]运用梁单元模型开发了一种简化的有限元模型模拟骨架层与抗压铠装层,研究径向压溃问题,并用试验与数值模拟结果进行验证。作者考虑了材料非线性问题,分别对ø101.6和ø203.2 mm骨架层进行模拟,分析了骨架层外压与其椭圆度之间的关系,并且建立了ø101.6 mm抗压铠装层与骨架层模型,考虑层间接触作用,忽略层间聚合物层的作用,加载径向压力进行模拟。模拟结果均小于试验所得临界压溃值,主要原因是其忽略聚合物层作用;具有抗压铠装层结构临界压溃值明显高于骨架层,这是因为其自身具有一定刚度,所以有助于骨架层抵抗外部抵抗力。
W.WANG等[8]考虑到骨架层实际结构复杂,在外载荷作用下会出现各向异性,将骨架层等效为正交异性圆柱壳结构,求出各个方向在外压作用下的弹性模量与泊松比表达式,根据J.A.WITZ等[9]给出的数据,求出弹性模量与泊松比在各个方向数值。
汤明刚等[10]使用弯曲刚度等效得到等效圆筒的厚度,运用圆环挠曲线微分方程计算出临界压溃值。建立骨架层三维有限元模型,分别对理想状态、存在初始椭圆度和考虑材料非线性等3种情况进行计算。运用弯曲刚度等效方法求得解析解,其与理想状态下骨架层压溃值误差在5%以内。在考虑初始椭圆度时,临界压溃值明显降低,并且随着初始椭圆度增大临界值逐渐降低。考虑材料非线性时,临界压溃值约为理想状态下的½。
M.G.TANG等[11]运用一种畸变能等效的方法研究骨架层临界压溃值,将具有复杂几何形状的骨架层转换为相等厚度的壳体结构。为了获得畸变能,开发了RVE有限元模型,并针对相同的边界条件推导出壳体结构分析方程。对3组不同骨架层样件进行径向压缩试验,验证该等效方法的有效性及安全性。通过对比,发现经过畸变能等效法计算出的等效厚度比试验确定的等效厚度小30%,与其他等效方法相比较,该种方法得出的结果较保守。
R.CUAMATZI-MELENDEZY等[12]分别对具有初始椭圆度骨架层和完整结构柔性立管进行压溃数值模拟。运用理论模型与骨架层数值模拟进行对比,对完整模型立管结构只建立有限元模型,目前并没有较好的理论模型。因外部抗压保护层的作用,所以具有完整结构立管临界压溃值要高于单个存在初始椭圆度的骨架层。单个骨架层理论模型与解析模型的主要区别在于材料非线性、相邻表面间的接触和剖面形状。数值模拟结果表明:完整结构立管临界压溃值高于带有椭圆度骨架层临界压溃值,差异约为6.7%。因此,建立完善的整体结构数值模型很有必要。
任少飞等[13]考虑骨架层铺设角度、初始椭圆度、材料非线性和不同接触方式,研究骨架层在均匀外压与径向压力下的失效特性。研究结果表明:骨架层相邻表面间接触条件对失效特性影响较大;铺设角度对骨架层失效特性的影响可忽略不计;考虑初始椭圆度和材料非线性后,均匀外压下骨架层临界压溃值大幅降低,径向压缩力下径向位移大幅增大。该方法可弥补理论方法无法考虑上述因素对骨架层失效特性影响的缺陷。
3 骨架层轴向撕裂失效骨架层中的轴向力依靠层与层之间接触所产生的摩擦力传递给外部的抗拉铠装层。挪威国家石油公司针对高温高压工作环境设计具有3层PVDF材料内衬层(由内至外依次为牺牲层、抗压保护层和抗变形层)非黏结柔性立管。该类立管经过一段时间工作后骨架层与终端装置焊接点下部区域出现了非螺旋状失效。在2013年OMAE会议上,首次提出骨架层撕裂这一新的失效模式并对其进行系统性的介绍,研究团队分析认为,骨架层呈现非螺旋状的主要原因是骨架层承担过大轴向力[14]。随着立管服役时间变长使得其内衬层中塑性材料损失,导致3层内衬层之间出现空隙,此时骨架层中轴向力无法依靠层与层之间接触摩擦力进行传递,从而造成骨架层承担过大轴向力而失效,如图 6所示。骨架层目前没有较好的轴向断裂理论模型,很多学者主要将数值模拟与试验相结合进行研究。
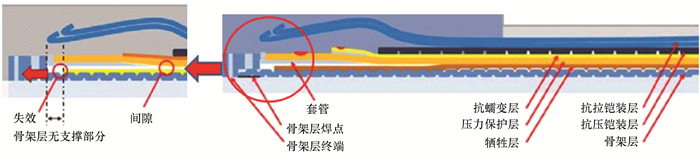
|
| 图 6 3层内衬层柔性立管骨架层轴向失效部位 Fig.6 Axial failure point of the flexible riser carcass layer with 3 layers of inner liner |
3.1 骨架层螺旋带模型
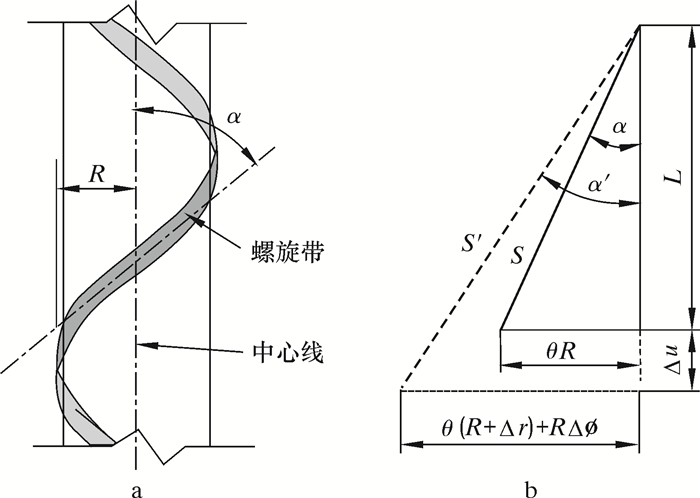
骨架层受轴向力作用时,不能再用圆柱壳理论模型进行等效计算,此时可考虑建立螺旋带模型[15],如图 7所示。
做以下假设:①轴向伸长率相同;②材料为各向同性线弹性材料;③应变和变形很小;④应力和应变均匀分布。将螺旋带展开成平面直线,在轴对称载荷作用下,螺旋带模型变形前、后形状如图 7所示。图中:S和S′为拉伸前、后长度,mm;θ为螺旋带缠绕角度,rad;R为骨架层节圆半径,mm;α和α′为拉伸前、后螺旋角度,rad;Δr为径向位移,mm。
由几何关系可知,螺旋带轴向应变为:
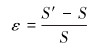
|
(15) |
其中:
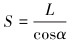
|
(16) |
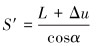
|
(17) |
式中:Δu为螺旋带轴向变形量。
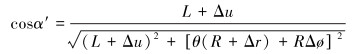
|
(18) |
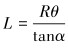
|
(19) |
基于以上假设可知螺旋带轴向应变为[15]:
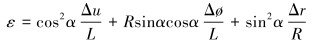
|
(20) |
由本构关系推出的轴向力表达式为:
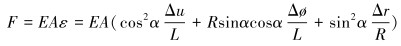
|
(21) |
螺旋带与立管轴向夹角为α,将螺旋带上轴向力向立管轴向投影,得到轴向力公式:
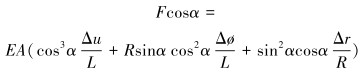
|
(22) |
螺旋带与立管轴向夹角为α,将螺旋带上轴向力向立管周向投影,得到螺旋带扭矩公式:
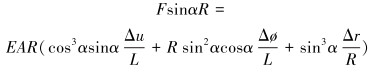
|
(23) |
扭转角度与扭矩关系式为:
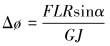
|
(24) |
螺旋角变化量Δα可表示为[16]:
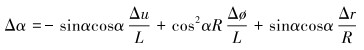
|
(25) |
根据弹性力学可知径向变化量为:
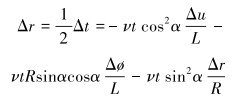
|
(26) |
式中:v为材料泊松比。
当单根螺旋带受轴向力作用时,可联立式(20)、式(21)、式(24)、式(25)和式(26)求解螺旋带各未知变量。
3.2 骨架层轴向失效国内外研究进展K.A.FARNES等[14]在2013年OMAE会议上首次对骨架层轴向失效进行了系统性的介绍。裸露在终端装置内部的骨架层,在焊接点的下部出现了非螺旋状,随后发生断裂。作者通过试验与理论分析,认为造成骨架撕裂的主要原因有4个:①骨架层与内衬层的重力;②在温度瞬间变化过程中,内衬层产生的温度应力;③压力作用下产生的轴向应力;④焊接点处存在的残余应力。但作者主要以案例分析与试验方法为主,缺少理论模型,没有对各个影响因素进行深入研究和分析。
G.SKEIE等[17]在2014年运用试验与有限元模拟相结合的方法研究骨架层轴向承载能力的大小。他们在研究中选取长度相等、内径不同的样件进行试验,其目的是验证没有外部支撑时骨架层轴向承载能力,分析骨架层失效过程,验证有限元模拟结果。他们运用ABAQUS和MARC对骨架层建模仿真,计算不同载荷下骨架层承载能力。经过试验与有限元模拟结果分析,得到骨架层承载能力与内径、骨架层轮廓和钢带厚度等相关,这与试验结论相符合。
C.E.KRISTENSEN等[18]建立有限元理论模型,考虑骨架层与牺牲层2层结构,将工况设定为降温作用下稳压立管模型,建立内衬层粘弹性材料弹性模量与热膨胀系数函数表达式。根据弹性力学中圆筒理论求出在温度与压力作用下牺牲层中产生的轴向力表达式。选取570 mm骨架样件进行中型尺寸试验,将有限元分析结果与试验结果进行比较,观察到两者之间存在差异主要由于试样样件热处理能力造成。在快速降温阶段,中型尺寸试验证明了牺牲层中会产生较大的轴向力,对于在降温情况下牺牲层材料的弹性模量与热膨胀系数起到了重要作用。
R.HANSEN等[19]在2015年针对骨架层失效机理,研究了考虑温度与重力作用时层与层之间产生的界面剪切应力。作者将模型简化为骨架层、内部层和外部层等3层二维平面,分别设2层之间的剪切应力为τ1、τ2。考虑重力与温度因素,求得界面在没有滑动与发生相对滑动2种工况下剪切应力表达式。同时考虑立管终端装置具有一定的隔热作用,分析了温度应力沿终端方向的变化规律,得到在终端两端处温度梯度最大,此时温度应力最大。由于内衬层采用复合材料,所以在建立切应力表达式时忽略了材料黏弹性特性。
R.PROVASI等[20]建立了厚度和平均半径与实际骨架层相等的圆柱壳模型进行等效替代。对轴向载荷(拉伸、压缩)作用下的实际骨架层进行计算,得到骨架层轴向、周向、径向弹性模量与泊松比,然后建立正交异性材料圆柱壳模型分析比较,结果显示仅周向应力与实际骨架层模型值较为接近。由于模型长度与厚度的原因,导致径向和轴向应力值与之存在差异。
C.E.KRISTENSEN等[21]基于之前对骨架撕裂进行了大量的中小型测试以及各种分析模型描述骨架撕裂现象。为了进行更全面的验证并且能够准确评估骨架撕裂模型,笔者选取长830 m的立管在周期变换的压力与温度环境下实施全尺寸试验。通过试验与有限元模拟得到温度从78 ℃降至11 ℃,压力从0增加到2.27 kN,骨架层中轴向力增加了约40 kN。影响骨架层中轴向力的主要因素包括:①内衬层弹性模量与泊松比;②材料热膨胀系数;③内衬层横截面积;④立管内部层与层之间的摩擦力。
4 结论与建议非黏结柔性立管作为水下生产系统重要组成部分,其特殊的结构及高技术含量引起国内外学者较高的关注。骨架层作为非黏结柔性立管最内层的运输通道,一旦失效将对整个立管结构产生破坏,给海洋油气生产系统带来巨大的经济损失。由于骨架层的特殊结构,研究其失效机理对立管设计具有重大意义。笔者对骨架层失效的国内外研究现状进行归纳总结,并提出一些建议,希望这些建议能够对下一步研究提供参考和帮助。
(1) 骨架层径向压溃失效理论模型较为完善,根据弹性理论中挠曲线微分方程可以求得径向压力作用与均匀外压下具有初始椭圆度骨架层径向位移表达式。建立骨架层轴向失效理论模型对于今后基础研究显得十分重要。在骨架层临近失效状态时其应力变化以非线性形式增长,对此处进行理论研究是今后的一个发展趋势。
(2) 通过对骨架层单个模型压溃研究与考虑整个立管模型进行压溃研究结果对比可知,骨架层临界压溃值存在明显差异。建立合适的完整立管模型进行数值模拟对于研究骨架层临界压溃值显得十分重要。
(3) 由于结构特殊性骨架层在外载荷作用下的力学性能会表现出各向异性,所以在单方向载荷作用下国内外学者根据其力学性能建立等效的正交异性材料模型进行研究分析,获得结果并不理想。今后可考虑在多载荷作用下对骨架层进行研究分析,完善并简化其等效模型。
(4) 可对不同立管结构进行更多的失效试验。在不同测试条件下,分别对骨架层、骨架层与抗压铠装层以及完整立管进行试验,通过试验获得的结果来验证数值模型的可靠性。
| [1] |
王彩山, 汤明刚, 阎军, 等. 海洋柔性管道骨架层径向压缩行为的数值模拟[J].
哈尔滨工程大学学报, 2015, 36(8): 1057-1061.
WANG C S, TANG M G, YAN J, et al. Numerical simulation of the radial compression of carcass layers of unbonded flexible pipes[J]. Journal of Harbin Engineering University, 2015, 36(8): 1057-1061. |
| [2] | TIMOSHENKO S P, GERE J M, PRAGER W. Theory of elastic stability, Second edition[J]. Journal of Applied Mechanics, 1962, 29(1): 220. |
| [3] | MARTINS C A, PESCE C P, ARANHA J A P. Structural behavior of flexible pipe carcass during launching[C]//Proceedingsof the 22nd International Conference on Offshore Mechanics and Arctic Engineering. Cancun, Mexico: ASME, 2003: 537-546. |
| [4] | NETO A G, DE ARRUDA MARTINS C. A Comparative wet collapse buckling study for the carcass layer of flexible pipes[J]. Journal of Offshore Mechanics and Arctic Engineering, 2012, 134(3): 031701. DOI: 10.1115/1.4005185 |
| [5] | PESCE C P, MARTINS C A, NETO A G, et al. Crushing and wet collapse of flowline carcasses: A theoretical-experimental approach[C]//Proceedingsof the 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China: ASME, 2010: 521-529. |
| [6] | MERINO H E M, DE SOUSA J R M, MAGLUTA C, et al. Numerical and experimental study of a flexible pipe under torsion[C]//Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China: ASME, 2010: 911-922. |
| [7] | NOGUEIRA V P P, NETTO T A. A simple alternative method to estimate the collapse pressure of flexible pipes[C]//Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China: ASME, 2010: 693-699. |
| [8] | WANG W, CHEN G. Analytical and numerical modeling for flexible pipes[J]. China Ocean Engineering, 2011, 25(4): 737-746. DOI: 10.1007/s13344-011-0059-9 |
| [9] | WITZ J A. A case study in the cross-section analysis of flexible risers[J]. Marine Structures, 1996, 9(9): 885-904. DOI: 10.1016/0951-8339(95)00035-6 |
| [10] |
汤明刚, 王野, 阎军, 等. 海洋柔性管道骨架层压溃的有限元分析[J].
哈尔滨工程大学学报, 2013, 34(9): 1135-1140.
TANG M G, WANG Y, YAN J, et al. Finite element analysis for collapse of flexible pipes carcass[J]. Journal of Harbin Engineering University, 2013, 34(9): 1135-1140. |
| [11] | TANG M G, LU Q Z, YAN J, et al. Buckling collapse study for the carcass layer of flexible pipes using a strain energy equivalence method[J]. Ocean Engineering, 2016, 111: 209-217. DOI: 10.1016/j.oceaneng.2015.10.057 |
| [12] | CUAMATZI-MELENDEZ R, CASTILLO-HERNÁNDEZ O, VÁZQUEZ-HERNÁNDEZ A O, et al. Finite element and theoretical analyses of bisymmetric collapses in flexible risers for deepwaters developments[J]. Ocean Engineering, 2017, 140: 195-208. DOI: 10.1016/j.oceaneng.2017.05.032 |
| [13] |
任少飞, 唐文勇, 薛鸿祥. 非黏结柔性立管骨架层失效数值计算方法[J].
上海交通大学学报, 2016, 50(3): 466-471.
REN S F, TANG W Y, XUE H X. Numerical method to predict failure of carcass layer of unbonded flexible risers[J]. Journal of Shanghai Jiaotong University, 2016, 50(3): 466-471. |
| [14] | FARNES K A, KRISTENSEN C, KRISTOFFERSEN S, et al. Carcass failures in multilayer PVDF risers[C]//Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes, France: ASME, 2013: V04AT04A024. |
| [15] |
郭有松, 陈希恰, 王德禹, 等. 非黏结柔性立管轴对称载荷作用下的结构响应和数值分析[J].
石油学报, 2015, 36(4): 504-510, 515.
GUO Y S, CHEN X Q, WANG D Y, et al. Analytical and numerical investigation on the structural response of flexible risers under axisymmetric load[J]. Acta Petrolei Sinica, 2015, 36(4): 504-510, 515. DOI: 10.7623/syxb201504012 |
| [16] |
陈希恰. 深海柔性立管结构力学特性分析[D]. 上海: 上海交通大学, 2014. CHEN X Q. Analysis of the mechanical property for deep-sea flexible riser[D]. Shanghai: Shanghai Jiaotong University, 2014. |
| [17] | SKEIE G, SKJERVE H, AXELSSON G, et al. Test validation of finite element analysis results of carcass axial capacity[C]//Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco, California, USA: ASME, 2014: V06BT04A048. |
| [18] | KRISTENSEN C E, MUREN J, SKEIE G, et al. Carcass tear out load model for multi-layer pressure sheath risers[C]//Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco, California, USA: ASME, 2014: V06BT04A012. |
| [19] | HANSEN R, LYCKEGAARD A, CAPPELN C, et al. Carcass tearing in flexible pipes[C]//Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering. St. John's, Newfoundland, Canada: ASME, 2015: V05AT04A041. |
| [20] | PROVASI R, TONI F G, DE ARRUDA MARTINS C. Equivalent model for interlocked carcass under axial loads[C]//Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering. Busan, South Korea: ASME, 2016: V005T04A007. |
| [21] | KRISTENSEN C E, MUREN J, GJENDAL A, et al. Full-scale validation of axial carcass loads in flexible pipe structure from cyclic pressure and temperature[C]//Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering. Trondheim, Norway: ASME, 2017: V05AT04A031. |