0 引言
近年来,随着信息技术的飞速发展,设备及系统的信息化、数字化成为各行各业发展的主流,石油行业中的智慧油田一经提出便获得了广泛的关注。随着对钻井设备安全与可靠性的要求日益提高,以数字化加强油田与平台的管理成为了当前发展的重要方向。石油钻机作为石油工业的核心设备之一,在近30年来也发生了深度变革,其结构朝着复杂化、精密化的方向不断发展。顶部驱动钻井装置(顶驱)是石油钻机的重大变革之一,其作为一种新型钻井驱动系统代替了传统的转盘,极大地促进了钻井作业的自动化,节省了钻井时间,提高了钻井作业能力和效率,目前已经广泛应用于深井钻井、复杂井钻井和海洋钻井之中[1]。然而,顶驱的安全问题也日益突出,作为海洋钻井平台的关键设备,一旦发生故障,不仅会造成停产,造成巨大的经济损失,严重时会导致钻井过程中出现重大失误,造成人员伤亡和设备损伤。因此,及时准确地掌握顶驱的状态十分重要。正常情况下顶驱为露天使用设备,在实际使用过程中将受到周围温度、湿度、盐分及腐蚀钻井液等环境条件的影响,且上下运动和变速、变载荷旋转等工况复杂,特殊情况下将在极为恶劣的环境下工作,对顶驱的状态监测造成了极大干扰。
齿轮箱作为顶驱中主要部件之一,其安全性一直是关注的重点,一旦发生故障将导致巨大的损失。2012年,某钻井平台在顶驱的使用过程中发现润滑油泵压力过低,且磁性滤器发生堵塞,在停机拆卸过程中清理出大量铁屑,之后发现齿轮箱下止推轴承上压盖出现裂纹,传动轴的滚柱轴承底部滚轮支架损坏,需要更换。事故造成顶驱停机无法使用,顶驱整体需全部拆解进行大修,更换上止推轴承。如果故障进一步发展,将导致齿轮箱内其他运动部件损坏,造成次生灾害,导致更长的停机恢复时间,并可能造成严重的井下复杂事故。由于齿轮箱的检测信号中包含齿轮和轴承的复合特征,如何准确地进行齿轮箱早期微弱故障分析及诊断值得研究。
传统的故障诊断方法为振动信号分析法,该方法以其时效性好、信号采集方便、故障模式容易确定及易于推广研究等特点广泛应用于各类机械设备的诊断之中[2-3]。但是传统的应用于振动信号的分解方法(如小波分解[4-5])只能拟合信号中的单一分量,而齿轮箱信号组成复杂,传统方法难以正确分析。2011年,共振稀疏分解(Resonance-based sparse signal decomposition, RSSD)法被提出,由于其对冲击信号的提取效果较好,被引入信号处理以解决传统方法存在的问题。但由于齿轮信号的调幅调频特性及振动信号的多级传递,导致共振稀疏分解法在拟合信号时对于混合着齿轮振动信号的低共振分量分析能力较差。
为了弥补这个缺陷,笔者提出了基于共振稀疏反褶分析的故障信号诊断方法,并引入最小熵反褶积理论,将其应用于齿轮箱故障诊断中。首先对所采集的齿轮箱信号进行时频域分析;然后对得到的信号进行共振稀疏分解,得到信号的高共振分量和低共振分量,并做包络分析,得到齿轮的故障特征频率;最后利用最小熵反褶积变换对低共振分量进行处理,使得低共振分量中的齿轮信号与轴承信号分离开来。齿轮箱故障模拟试验以及实例验证表明,该方法可以有效提取齿轮箱的冲击信号特征,提高了故障识别率。
1 顶驱故障树构建顶驱的故障大致可分为机械故障、电气故障和液压故障3种,其故障树如图 1所示。由于机械故障的种类和复杂程度要大于其余2类故障,且都是顶驱关键部件,一旦发生将极大地影响钻井作业的正常进行;而且由于机械结构的复杂性,维修时间往往较长。据统计,某海上钻井服务公司2017年共发生47起顶驱故障,平均每月4起,其中机械类故障34起,占到了72.34%。因此,对于机械部分的状态监测与诊断十分必要。
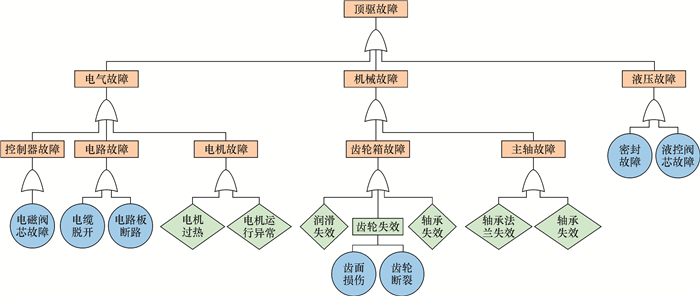
|
| 图 1 顶驱故障树 Fig.1 Fault tree of top drive |
较严重的机械故障通常会导致停机事件的发生,并且在确定故障以及检修维护的过程中往往需要进入设备大修流程,从而导致较高的维护费用以及停机损失。而且,故障恶劣情况将会随着检修时间的延迟而被发展放大,所造成的后果也会更加严重。因此,对于机械故障进行数字化监测诊断,利用大数据平台对其进行状态评估十分重要。
相对其余2类故障而言,机械故障可以通过对传感信号进行诊断分析来判断设备的状态,具有一定的可监测性和可预防性。
2 共振稀疏反褶分析方法笔者在完成齿轮箱故障信号采集之后,首先利用共振稀疏分解对原始信号进行处理,将其分为高、低共振分量2个信号。由于齿轮故障信号具有持续振荡性,往往存在于高共振分量中,而轴承故障信号由于具有瞬态性,往往分布于低共振分量中。之后对分离出的2个信号做包络谱分析,分析信号中所包含的齿轮故障特征频率。由于包含轴承故障信息的低共振分量中混杂了一定的低能量齿轮冲击信号,所以无法直接提取出明显的轴承故障特征。对此,利用最小熵反褶积变换对低共振分量进行处理,加强冲击分量,再对处理后的信号进行包络分析,从而提取出轴承的频率特征信息,完成齿轮箱中齿轮与轴承的诊断。图 2为基于共振稀疏反褶分析的齿轮箱故障诊断流程图。
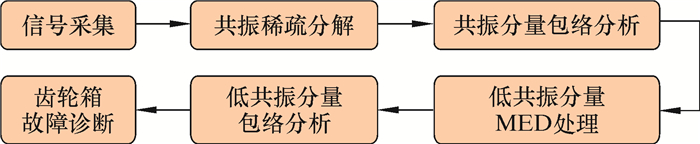
|
| 图 2 基于共振稀疏反褶分析的齿轮箱故障诊断流程图 Fig.2 Flowchart of fault diagnosis of top drive gearbox based on minimum entropy deconvolution resonance-based sparse signal decomposition |
2.1 共振稀疏分解
共振稀疏分解是由I.W.SELESNICK为了医学领域的心脏信号诊断而在2011年最早提出的[6]。区别于传统频率滤波分解依照频率高低来进行分解的方法,共振稀疏分解法是通过对原信号的波形振荡特性(振荡次数)进行原始信号拟合,其拟合过程结合了可调Q因子小波(Tunable Q-factor Wavelet Transform, TQWT)和形态分量分析(Morphological Component Analysis, MCA),可将原始信号在分解过程中依据振荡次数多少分为高共振分量与低共振分量,并且能够有效分离中心频率相近而带宽不同的信号分量。
通过共振稀疏分解进行信号的处理公式如下:

|
(1) |
式中:W1和S1分别代表高品质因子Q1的系数矩阵和其对应的TQWT基函数库,W2和S2分别代表低品质因子Q2的系数矩阵和其对应的基函数库,n表示不能拟合的残余信号。
如果基函数库S能够很好地拟合原信号,则系数矩阵W中的很多元素都会很小,矩阵W中接近0的元素越多,认为系数矩阵W越稀疏。从而可以将式(1)称为信号y的稀疏分解。
该公式可以看成是寻求最佳的系数矩阵W1和W2的过程。这2个系数矩阵可通过文献[7]中提出的目标函数来求解:
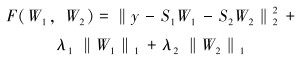
|
(2) |
该目标函数F的寻优过程可由分裂增广拉格朗日收缩算法(SALSA)来迭代实现。当迭代收敛时,高、低共振分量可以分别表示为:
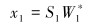
|
(3) |
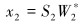
|
(4) |
式中:W1*和W2*是最终获得的系数矩阵。
分离振动信号依靠形态分量分析来完成,可调Q品质因子小波的主要作用是通过选择不同的品质因子Q来构建较合适的小波基函数库,从而保证信号分解结果的稀疏性。一系列具有相同高品质因子的小波基函数线性叠加组成了高共振分量,相对的,低共振分量则是由一系列具有相同低品质因子的小波基函数线性叠加而成。其中,品质因子Q代表信号中心频率和带宽的比值,其表达式为:
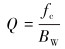
|
(5) |
式中:fc为信号振荡的中心频率,BW为中心频率对应的带宽。
但是对于零部件较多的齿轮箱而言,由于所采集的振动信号中多种特征频率混杂,共振稀疏分解难以完全拟合具有调幅调频特性的齿轮故障信号。因此,笔者提出了一种最小熵反褶积辅助的共振稀疏分解法来进行齿轮箱的故障诊断。
2.2 最小熵反褶积顶驱齿轮箱在故障工况下的振动信号特征表现为脉冲冲击,而这一特征往往被其他信号所淹没,例如齿轮啮合信号等,进而导致特征提取困难。笔者引入最小熵反褶积来突出信号中的强冲击信号,并且将信号的峭度值作为迭代终止条件,以此用于轴承冲击信号的提取。
设故障冲击信号如下式所示[8]:
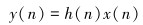
|
(6) |
式中:x(n)为故障冲击信号,h(n)为信号处理过程中系统脉冲响应函数,y(n)为x(n)经过传递路径以及噪声共同影响后检测到的信号,变化过程使得信号的熵变大。
最小熵反褶积变换的目标是通过迭代运算得到一个最优的逆滤波器f(n),对y(n)进行逆运算,使得信号x(n)的熵最小,即有:
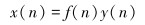
|
(7) |
运算得到的x(n)的峭度值可以作为迭代寻优的目标函数[9]:
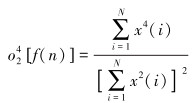
|
(8) |
式中:N为信号长度。
将式(8)对f(n)求偏导,得到信号极大值点如下所示:
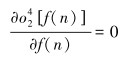
|
(9) |
利用逆滤波器对冲击故障信号进行反褶积计算,即有:
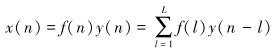
|
(10) |
式中:L为滤波器长度。
由式(9)和式(10)可得:
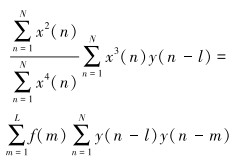
|
(11) |
式(11)可以表示为矩阵形式:

|
(12) |
式中:g为滤波器输出的立方与输入的互相关的加权和,R为故障冲击信号的Toeplitz自相关矩阵,可以得到滤波器系数:

|
(13) |
通过多次迭代求得x(n)的最合适的一个极大值,即是所求的冲击信号,迭代的次数一般选取4~6次。
3 模拟分析 3.1 齿轮故障模拟在理想状态下,齿轮的振动方程可以表示为:
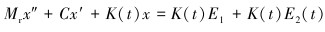
|
(14) |
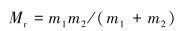
|
(15) |
式中:Mr为啮合齿轮的等效质量,x为沿力的作用线方向上齿轮的相对位移,C为齿轮的啮合阻尼系数,K(t)为啮合刚度,E1为齿轮受载后的平均静弹性变形,E2(t)为故障相对位移函数,指2个齿轮之间因计算差量或者故障变形位移导致的距离改变,m1和m2为相互啮合齿轮的质量。
由于齿轮信号式中包含啮合频率成分,而齿轮振动主要是因为啮合刚度K(t)的改变,且啮合刚度会随着转动1周内啮合点与齿数的改变而周期性改变,使得振动信号也具有了周期性。设一对齿轮其输入轴与输出轴的转动频率分别为f1和f2,齿数分别为Z1和Z2,则其啮合频率fz可表示为:
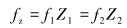
|
(16) |
为了使仿真信号更加真实,加入齿轮倍频信号,得到如下表达式:
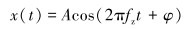
|
(17) |
式中:A为振动幅值,φ为初始相位。
故障情况下,由于存在着幅值调制和频率限制,式(17)又可表示为:

|
(18) |
式中:B为幅值调制系数,β为频率调制系数(弧度制),fr为故障轴转频。
之后加入轴承信号与噪声信号,最终得到齿轮箱故障仿真信号:

|
(19) |
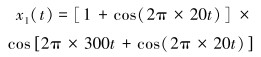
|
(20) |

|
(21) |
式中:n(t)为噪声信号,x1(t)为仿真齿轮故障信号,x2(t)为200 Hz的轴承故障仿真信号,e(t)为以系统共振频率为载波的指数衰减函数,M为采样信号中含有的脉冲次数,T为周期,x(t)为加噪后的齿轮轴承故障仿真信号。
设置轴转频20 Hz,啮合频率为300 Hz。信噪比为4.2。采样频率为10 kHz,采样点数为4 096。仿真信号如图 3所示。

|
| 图 3 齿轮故障仿真信号 Fig.3 Simulation signal of gear fault |
3.2 共振稀疏分解
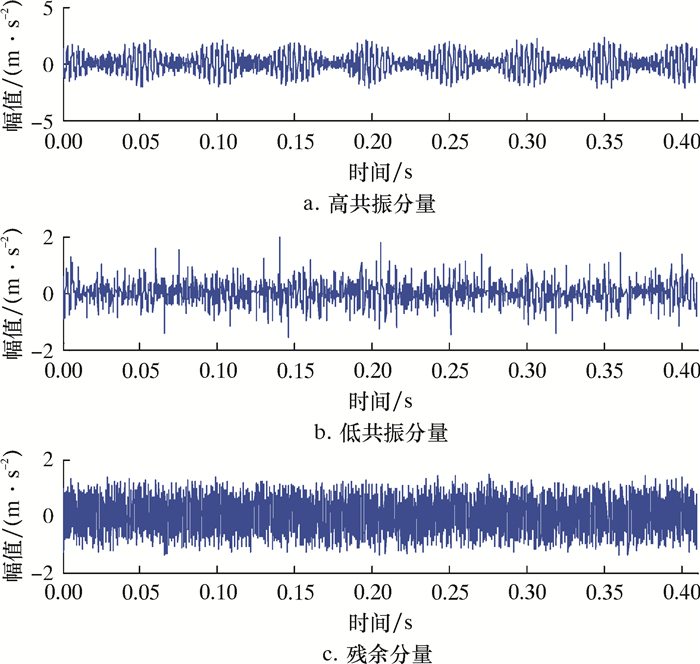
对得到的模拟信号进行共振稀疏分解,令最佳品质因子参数Q1为6.623 3,Q2为1,高、低共振分量修正参数均取为0.5。最终的分解结果如图 4所示。
|
| 图 4 共振稀疏分解结果图 Fig.4 Results of resonance-based sparse signal decomposition |
对稀疏分解后的信号的高、低共振分量进行包络谱分析,结果如图 5所示。

|
| 图 5 共振分量包络谱 Fig.5 Envelope spectrum of resonance component |
从图 5可以看出,高、低共振分量的包络谱中都包含了转频为20 Hz的调幅信号,表明齿轮的故障信号得到了有效提取,但低共振分量中混合了很大一部分无法彻底拟合齿轮冲击的故障信号,导致400与600 Hz的轴承故障2倍频与3倍频不明显。
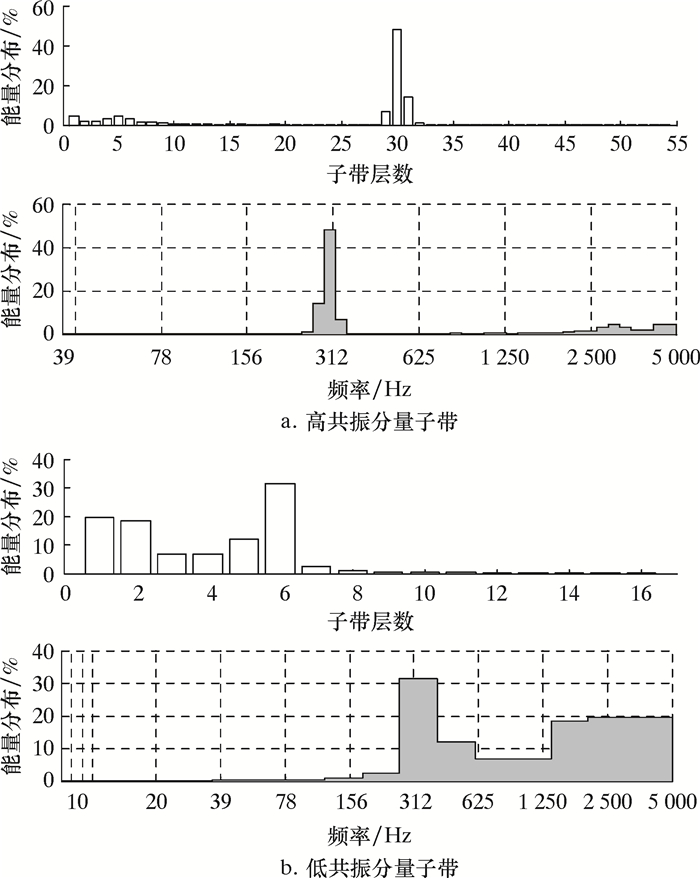
3.3 能量子带分析能量子带分析是通过分析得到的高、低共振分量的能量子带,提取并重构包含故障特征的能量子带[10],再从重构的信号中提取故障特征频率的方法。对稀疏分解之后的高、低共振分量进行能量子带分析,得到高、低共振分量的能量子带,结果如图 6所示。
|
| 图 6 共振分量能量子带分析图 Fig.6 Energy sub-band analysis of resonance component |
子带能量分布图反映了共振分量子带能谱及其对应的频率分量大小。从图 6可以看出,不同的振动分量包含的能量集中的层数差距很大,高共振分量子带能量集中在29~31层,而低共振分量的能量主要集中在1~6层上。对此重构高、低共振分量能量子带的信号分析发现,高共振分量的重构信号高度还原了齿轮的模拟故障信号,对1~3和4~6层对应频率分别提取并做包络分析,1~3层的包络图中可以明显看出200.2 Hz的轴承故障冲击信号,4~6层中的时域图则发现齿轮故障模拟信号较为明显,并存在300 Hz的齿轮故障信息以及20 Hz的边频带,这些能量的产生是高共振分量未能完全拟合故障冲击信号,部分齿轮故障信号泄漏到低共振分量中所致。
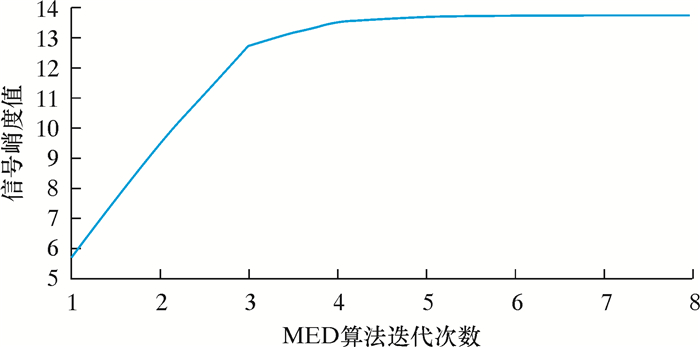
3.4 最小熵反褶积处理对于混合了未能被很好拟合的低能量齿轮振动信号的低共振分量部分,直接对其做包络分析存在一定干扰,因此使用最小熵反褶积对其进行处理,保留信号中峭度分量,抑制夹杂的齿轮信号,削弱信号中的振荡分量,加强冲击分量。最小熵反褶积求解迭代最佳次数的过程如图 7所示。
|
| 图 7 最小熵反褶积迭代分析 Fig.7 Iterative analysis of minimum entropy deconvolution |
由图 7可知,最小熵反褶积的最佳迭代次数为5次,接着利用其对得到的低共振分量处理,加强冲击信号,并将得到的信号进行包络分析,得到的结果如图 8所示。

|
| 图 8 最小熵反褶积处理效果图 Fig.8 Processing results of minimum entropy deconvolution |
由图 8可以看出,经过最小熵反褶积处理后的包络谱去除了齿轮信号的干扰,各特征频率相对于子带分析更加明显,幅值更大,且最小熵反褶积无需各种复杂的人为选择等步骤,使用更加简便。
4 试验验证 4.1 试验设置设置齿轮箱试验台模拟齿轮故障信号,试验台设置如图 9所示。齿轮箱试验台为斜齿轮2级减速传动机构,第1级的齿数比为16:48,第2级齿数比为24:40。其中,第2级齿轮为正常齿轮,第1级齿轮为故障齿轮,故障设置为断齿。高速轴处轴承型号为MB Manufacturing ER-10K,含8个滚子,每个滚子直径为7.937 5 mm,轴承节径为33.502 6 mm,接触角为0°,轴承故障设置为内圈点蚀故障。选用的加速度传感器为Endevco 10mv/g Accel,设置采样的频率为66.667 kHz,采样点数为30 000。

|
| 图 9 齿轮箱试验台 Fig.9 Gearbox test bench |
设置电机转速为3 000 r/min,并加高负载,采集高速轴轴承内圈和输入端齿轮断齿复合信号,并做傅里叶变换,得到信号的频域图如图 10所示。
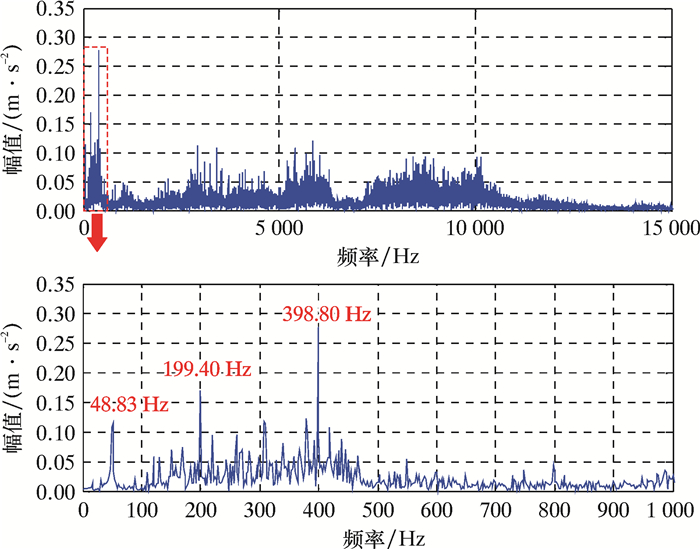
|
| 图 10 复合故障信号频域图 Fig.10 Frequency domain diagram of composite fault signals |
从图 10可以看出,0~1 000 Hz的低频部分中存在着48.83 Hz的高速轴转频、199.40 Hz的低速轴半倍啮合频率以及398.80 Hz的低速轴啮合频率。1 000 Hz以上的高频段成分复杂,能量较多,包含了3 200 Hz左右的高速轴啮合频率的4倍频,6 400 Hz左右的高速轴啮合频率8倍频以及8 000 Hz左右的系统共振频率。因此,传统方法难以将齿轮与轴承特征频率有效地分离提取,从而进行齿轮箱故障的准确诊断。
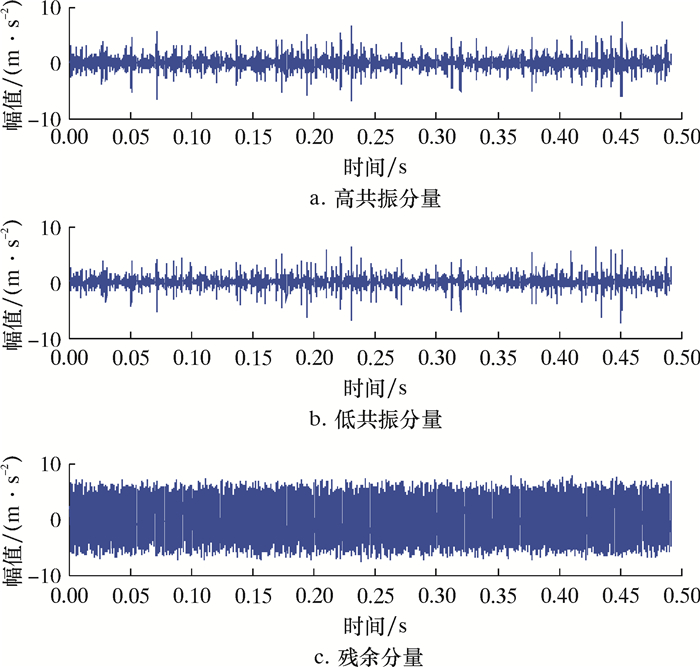
4.2 共振稀疏反褶分析对上一步所采集到的振动信号进行共振稀疏分解,设置高品质因子Q1=3.762 6,Q2=1,高、低共振分量修正参数均为0.5。共振稀疏分解结果如图 11所示,对高共振分量进行包络谱分析,结果如图 12所示。
|
| 图 11 信号共振稀疏分解结果图 Fig.11 Envelope spectrum of high resonance component |

|
| 图 12 高共振分量信号包络谱图 Fig.12 Envelope spectrum of high resonance component |
从高共振分量包络谱中可以明显看到转子转频分量及其倍频信号和398.8 Hz的低速轴啮合频率,可以判断高速轴齿轮可能存在故障。
对低共振分量做最小熵反褶积变换,并对处理后的信号进行包络分析,结果如图 13所示。

|
| 图 13 低共振分量包络谱分析图 Fig.13 Envelope spectrum of low resonance component |
由图 13可看出,在低共振分量的包络谱中发现246.2 Hz的轴承内圈故障特征频率十分明显,同时发现该特征频率的2倍频也清晰可见。由此可以得出结论,经过高品质因子寻优及最小熵反褶积优化处理之后的共振稀疏分解法具有有效提取齿轮故障特征与轴承故障特征信号的能力,证明了笔者所提出方法的有效性。
5 结论(1) 利用共振稀疏分解能够有效地将组成复杂的齿轮箱故障信号分为高共振分量和低共振分量信号。通过对高、低共振分量信号进行包络分析,在高共振分量的包络谱中有效地提取出了齿轮故障特征频率,提高了齿轮故障诊断的准确性。
(2) 利用最小熵反褶积优化低共振分量信号后,有效地加强了其中的齿轮箱轴承工作过程中的冲击信号,排除了信号分解后齿轮高共振分量混入低共振分量中而导致的干扰,解决了传统诊断方法只能拟合高共振分量信号的问题。
(3) 利用所提出的方法进行了齿轮模拟故障信号及齿轮箱试验台故障诊断试验,成功地诊断出齿轮断齿故障及齿面磨损故障的复合故障,这表明笔者所提方法可以有效地提高齿轮箱复合故障的诊断能力。
| [1] |
陈朝达.
顶部驱动钻井系统[M]. 北京: 石油工业出版社, 2000, 1-66.
CHEN C D. Top drive drilling system[M]. Beijing: Petroleum Industry Press, 2000, 1-66. |
| [2] |
朱繁泷. 基于振动信号的旋转机械运行状态趋势分析与故障诊断[D]. 南昌: 江西理工大学, 2014. ZHU F L. Research on vibration signals for rotary machinery condition monitoring and fault diagnosis[D]. Nanchang: Jiangxi University of Science and Technology, 2014. |
| [3] |
冯志鹏, 宋希庚, 薛冬新, 等. 旋转机械振动故障诊断理论与技术进展综述[J].
振动与冲击, 2001, 20(4): 36-39.
FENG Z P, SONG X G, XUE D X, et al. Survey of vibration fault diagnosis of rotational machinery[J]. Journal of Vibration and Shock, 2001, 20(4): 36-39. |
| [4] | ERISTI H. Fault diagnosis system for series compensated transmission line based on wavelet transform and adaptive neuro-fuzzy inference system[J]. Measurement, 2013, 46(1): 393-401. DOI: 10.1016/j.measurement.2012.07.014 |
| [5] |
王仲生, 何红, 陈钱. 小波分析在发动机早期故障识别中的应用研究[J].
西北工业大学学报, 2006, 24(1): 68-71.
WANG Z S, HE H, CHEN Q. Exploring effective early identification of aero-engine rotor faults[J]. Journal of Northwestern Polytechnical University, 2006, 24(1): 68-71. |
| [6] | SELESNICK I W. Resonance-based signal decomposition:A new sparsity-enabled signal analysis method[J]. Signal Processing, 2011, 91(12): 2793-2809. DOI: 10.1016/j.sigpro.2010.10.018 |
| [7] | BAYRAM I, SELESNICK I W. Frequency-domain design of overcomplete rational-dilation wavelet transforms[J]. IEEE Transactions on Signal Processing, 2009, 57(8): 2957-2972. DOI: 10.1109/TSP.2009.2020756 |
| [8] |
王志坚. 齿轮箱复合故障诊断特征提取的若干方法研究[D]. 太原: 太原理工大学, 2015. WANG Z J. Research on some new methods in fault diagnosis of gearbox with compound faults[J]. Taiyuan:Taiyuan University of Technology, 2015. |
| [9] | WIGGINS R A. Minimum entropy deconvolution[J]. Geoexploration, 1978, 16(1/2): 21-35. |
| [10] |
孙云嵩. 基于信号共振稀疏分解的齿轮故障诊断方法研究[D]. 长沙: 湖南大学, 2013. SUN Y S. Research on the fault diagnosis methods of gears based on resonance-based sparse signal decomposition[D]. Changsha: Hunan University, 2013. |



