2. 中国石油天然气销售东部分公司;
3. 中国石油西气东输管道公司
2. Marketing Eastern Company, PetroChina;
3. West-East Pipeline(Marketing) Company, PetroChina
0 引言
天然气长输管道压气站内的喘振控制系统是避免压缩机发生喘振,保证设备安全、平稳运行的重要装置。实际压气站喘振控制系统的设计及相关设备的选型往往缺乏理论依据,因此需要对其进行研究,重点分析各设备的性能对喘振控制系统总体性能的影响,从而为离心式压缩机组喘振控制系统的建立提供依据。
国外众多学者已经对压缩机喘振控制系统进行了大量研究。较为典型的是F.K.MOORE等[1]针对轴流式压缩机建立的低阶非线性动态参数模型,通过研究分岔特性(bifurcation characteristic)获得压缩机系统的非线性动力学特性,目前已广泛应用于压缩机稳定系统的分析和设计,但该模型没有考虑压缩机流扰动与产生的压力扰动之间的时间间隔,且将流体视为不可压缩流体,仅适用于低速压缩机。E.H.ABED等[2]在低阶非线性动态参数模型的基础上,应用旋转失速和喘振动力学中经典非线性动力学理论,建立了一种旋转失速和喘振控制简化模型,大大减少了计算量。K.M.EVEKER等[3]在工业涡轮机械的安装过程中验证了其正确性。为克服非线性模型的弊端,A.H.EPSTEIN等[4]充分考虑了流扰动与压力扰动的时间间隔,基于线性化方法,建立了动态喘振控制系统。文献[5-6]通过系统识别和控制系统设计将该线性化模型应用到工程实际中,验证了其正确性。这些早期的研究主要利用较为简单的动态模型作为建立压缩机防喘振系统的尝试,对压缩机稳定运行具有重要意义。
随着相关研究的不断发展,R.KURZ等[7]提出用简化模型进行喘振控制系统模拟,其核心思想是将压缩机排气端、防喘阀及下游单向阀间的管道内部容积简化为一个固定容积空间,利用模型计算通过阀门和压缩机的流量,但并不准确计算管道内气体的流动。该简化模型以较少的计算量获得了喘振控制系统特性与排气容积和防喘阀特性之间的关系,但计算精度未得到试验验证。另一类典型研究方法是利用计算流体力学方法对管道内的流动进行动态计算,通过对阀门、压缩机、空冷器、弯头和变径管等部件分别进行建模,衡量管道内流动对于紧急停机等事件的响应。K.BOTROS等[8-9]是此类研究路线的代表性研究学者,他们采用特征线方法对管道流动控制方程进行求解,并采用准定常方法对各类部件进行模拟。L.ZHANG[10]对管道内流体采用有限体积法高阶迎风格式求解控制方程,对于离心式压缩机和阀门等部件则分别建立了准定常模型,分析了压缩机管道防喘振系统的性能,结果显示压缩机工况点和压力等模拟结果在压缩机紧急停机初始阶段与试验数据的差异不超过10%,验证了当前模型用于评估压缩机防喘振性能的准确性。
笔者在对压缩机管路布置方案准确建模的基础上,采用有限体积法对管道流动控制方程进行求解,控制方程引入了壁面摩擦和传热对流动的影响;对于压缩机采用准定常的方法计算其对管道流动的影响,模拟压缩机特性随时间的变化。利用所得计算程序动态模拟紧急停机过程中气体在管道内的流动,分析喘振控制系统的性能及其用于避免压缩机组喘振的可靠性和有效性。
1 数学模型 1.1 管道流动控制方程直管道是管道增压系统及喘振控制系统的主体,其内部流动采用一维非定常可压缩流动的守恒型控制方程,包括连续性方程、动量方程以及能量方程。
连续性方程:
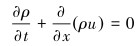
|
(1) |
动量方程:
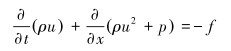
|
(2) |
能量方程:
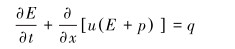
|
(3) |
式中:u为速度,f和q分别为单位体积的摩擦力及对流换热速率,分别用于计入管道壁面摩擦和传热对于流动的影响,ρ为流体密度,E为包括气体内能和动能的总能量。
引入表面摩擦因数Cf(Fanning friction factor)计算f,其定义为:
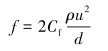
|
(4) |
式中:d为管道内径。
式(3)中的q通过下式计算:
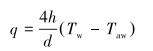
|
(5) |
式中:Tw为壁面温度,Taw为绝热壁面温度,h为对流传热的膜系数。
对于管道的湍流流动,h可以通过如下关联式计算。
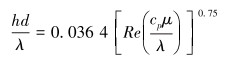
|
(6) |
式中:λ为阻力系数,μ为流体黏度。
1.2 管道流动数值计算模型基于有限体积法,采用较为典型的迎风格式——Roe流量差分(Roe flux differencing)格式[11]对管道流动控制方程(1)~(3)进行求解。为了推导控制方程的Roe差分计算格式,首先得到其雅克比矩阵:
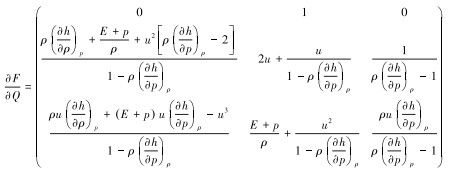
|
(7) |
上述矩阵存在以下3个特征值:
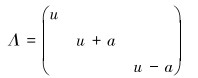
|
(8) |
式中:a为声速。
式(7)中,雅克比矩阵存在3个特征向量,即:
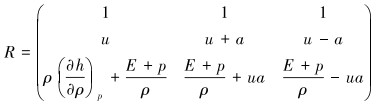
|
(9) |
矩阵R的逆矩阵为:
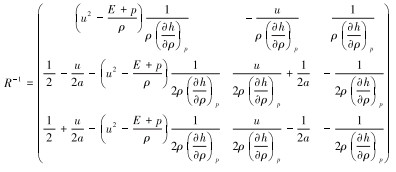
|
(10) |
在直管道长度方向上对计算域进行均匀离散,网格密度可根据计算精度需要进行调整。根据Roe格式,在网格单元交界上的数值通量通过式(11)计算:
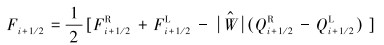
|
(11) |
式中:下标i+1/2、i-1/2均为网格的交界面,上标L、R分别为守恒变量在交界面左、右侧的值,取为交界面左、右侧网格单元的平均值。
为实现更高阶的计算精度,采用MUSCL格式重构得到上述交界面两侧的守恒变量值,最高可实现三阶计算精度。
MUSCL格式具体表述为:
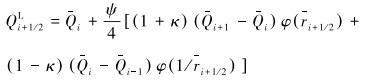
|
(12) |
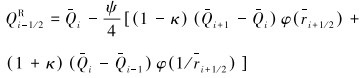
|
(13) |
其中: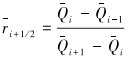
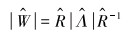
|
(14) |
式中: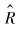
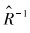
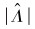
由于实际部件内部几何形状较为复杂,所以采用准定常计算方法对部件进行模拟,即部件的端口之间在任意时刻存在直接的能量及质量守恒关系,不同端口的参数之间根据部件特性也存在直接联系。在计算过程中,各部件起到连接管道流动的作用。从入口管道流动中获取流动及状态参数,根据其特性及准定常方程进行求解,从而为出口管道流动计算提供边界条件。由于部件内部流动长度远小于管道内流动尺度,能够更为迅速地响应流场内的瞬态变化,所以准定常模型是合理的计算方法。对于天然气管道压气站,主要考虑限流型、容积型、离心式压缩机及三通型4类部件。
离心式压缩机的作用在于对气体做功、提高其压力和温度。离心式压缩机的气体压缩过程是一个多变过程,其多变效率根据多变指数有如下定义[12]:
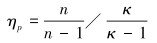
|
(15) |
式中:n为多变指数,κ为等熵指数。
离心式压缩机的多变能量头由下式定义[12]:
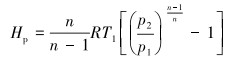
|
(16) |
式中:p2/p1=r,为压缩机的压缩比,T1为入口端温度。
若压缩机的多变效率和能量头已知,则压缩机压缩比r和温度比可通过式(16)计算获得。多变效率和能量头根据当前工况下的压缩机转速和进口体积流量由压缩机特性曲线获得。由于大多数压缩机组仅具备特定转速下的有限个数点的实测性能数据,所以首先利用三次多项式对实测性能数据进行拟合,由风机相似定律推算得到压缩机在不同转速下的性能曲线,进而得到多变效率和能量头关于转速和流量的函数关系,即:η=η(Q, N)和H=H(Q, N)。此外,根据质量守恒,压缩机吸气端和排气端的气体质量流量存在如下关系:
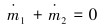
|
(17) |
式中:m1和m2分别为压缩机吸气端和排气端的气体质量流量。
在压缩机正常运转过程中,如果其驱动机突然失去动力(燃气轮机切断燃料或者电动机断电),则将发生压缩机的紧急停机(Emergent shutdown, ESD)事件,其转子转速迅速下降,是压气站中对喘振控制系统的防喘振性能要求最高的过程,因此模拟紧急停机过程中喘振控制系统的性能是评价喘振控制系统性能的重要依据。在紧急停机过程中,需求解转子转速随时间的变化规律,根据风机相似定律,有下式:
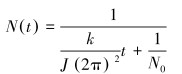
|
(18) |
式中:N(t)表示转速,N0为初始转速,J为转动惯量,k为比例系数。
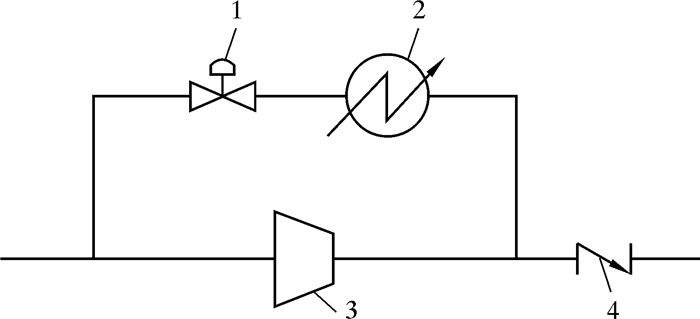
3 实例分析以中卫天然气压气站的喘振控制系统为例进行分析。中卫压气站是西气东输工程的重要枢纽,站内为西气东输一线配备由Rolls-Royce提供的天然气管道增压系统,核心部件为RF36型离心式压缩机,配备1台RB211型燃气轮机作为驱动机。中卫压气站的喘振控制管路方案如图 1所示。由图可知,中卫站喘振控制系统的特点是在防喘管路上设置了1台专用空冷器,核心部件是防喘阀。中卫站的实际管路布置方案还涉及多个弯头、变径管和球阀等部件,但未在图中显示。
|
| 图 1 中卫压气站喘振控制系统布置方案示意图 Fig.1 Schematic diagram of the arrangement of the surge avoidance system in gas compression station 1—防喘阀;2—冷却器;3—压缩机;4—单向阀。 |
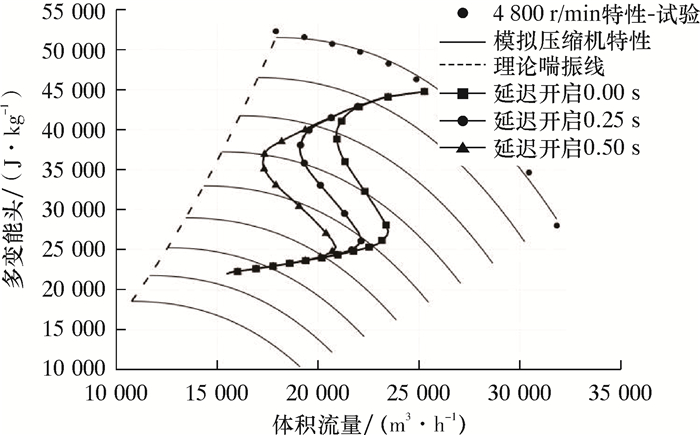
首先对中卫压气站的详细管路布置方案进行分析,得到了管道尺寸、部件特性以及管道-部件连接情况等数据,并根据这些数据建立了计算模型。计算压缩机特性的试验数据依据为图 2中转速为4 800 r/min下的多个离散特性点,使用三次曲线方法对其进行拟合,并利用风机相似定律推算其他任意转速下的特性。
|
| 图 2 防喘阀开启延迟时间对喘振控制的影响 Fig.2 Effect of anti-surge valve opening delay time on surge avoidance |
在压缩机的停机过程开始之后,通过开启图 1中防喘阀进行喘振控制。在真实的控制过程中,阀门的开启往往存在一定的延迟时间,即其接到开启指令的时刻起,直到产生实际大于0的开度所需时间。为研究防喘阀开启的延迟时间对喘振控制系统性能的影响,首先模拟计算了防喘阀不同开启延迟时间下的停机过程,所得压缩机工况点的轨迹如图 2所示。
由图 2可知,防喘阀的开启延迟时间对喘振控制系统的总体性能有重要影响。延长开启延迟时间意味着系统的反应更为迟缓,不能及时抑制压缩机流量的减小趋势,系统的可靠性受到影响,尤其对于停机过程的初始阶段,相同转速下压缩机的工况点更加接近于喘振线,发生喘振的风险更大。在压缩机进气流量回到峰值之后,各条工况点的轨迹归于一致,表明防喘阀开启延迟时间对于此后的压缩机进气流量没有影响。
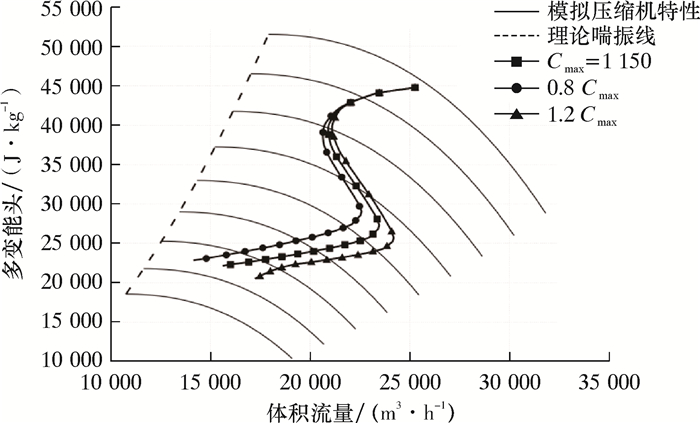
除开启延迟时间之外,最大流量系数Cmax也是防喘阀的重要特性参数。为研究防喘阀的最大流量系数对喘振控制系统性能的影响,重复中卫站压缩机组停机模拟,分别使用0.8倍和1.2倍原防喘阀最大流量系数进行计算,得到压缩机工况点的轨迹如图 3所示。从图可以看出,防喘阀最大流量系数反映了喘振控制系统的有效性,较大的流量系数可以明显提高停机过程中压缩机的进气流量并且使其在整个过程中一直保持相对较高的水平。因此,较大的流量系数可使压缩机在停机过程中总体更加远离喘振工况。
|
| 图 3 防喘阀最大流量系数对喘振控制的影响 Fig.3 Effect of maximum flow coefficient of anti-surge valve on surge avoidance |
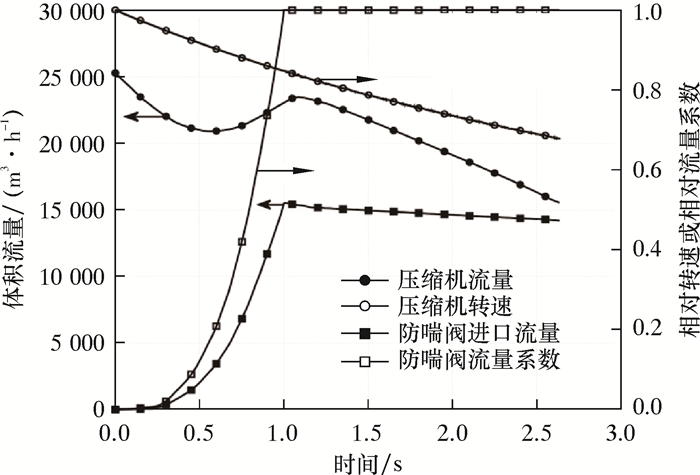
图 4所示为停机过程中压缩机和防喘阀特性随时间变化趋势及各自进气流量的历史数据,能够反映2个部件间的相互作用规律,数据均取自图 2中阀门开启延迟时间为0 s的算例。从图可以看到,防喘阀的进口气体流量基本遵循其开度随时间的变化规律,在开度达到最大之后其通流流量也达到最大值,同时使压缩机的进气流量稍后回升到一个峰值,此后压缩机进气流量以一个相对初始停机阶段较慢的速率持续减小。
|
| 图 4 停机过程中压缩机和防喘阀特性及入口流量随时间变化规律 Fig.4 Behavior of the compressor and anti-surge valve and the inlet flow rate over time during shutdown |
由以上讨论可以知道,当利用喘振控制系统对停机过程中的压缩机进行喘振控制时,压缩机工况点的变化规律是管路布置方案中各个设备的特性对管道内气体流动影响的综合表现。除重点讨论的防喘阀特性之外,方案中涉及到的其他设备均会对其造成一定影响[13],因此在实际天然气压气站的设计、设备的选型和安装过程中,需要对管道布置方案进行完整的建模并且准确计算各部件的特性,最后根据停机过程的模拟计算结果判断喘振控制系统的性能。
4 结论(1) 通过模拟研究压气站喘振控制系统的性能,提出了关于压气站管道内气体流动的模拟计算理论,即对于管道内流动采用有限体积法进行模拟,所用数值计算格式考虑了天然气作为真实气体的物理性质及管道壁面的摩擦和传热对流动的影响。
(2) 针对压缩机给出了相应的准定常模型及特性的计算方法,用于衡量部件对管道内气体流动的影响。
(3) 进一步利用压气站管道内流动计算模型对西气东输中卫站的实际喘振控制系统进行分析。分析结果表明:防喘阀的开启延迟时间和最大流量系数对于喘振控制系统的总体性能有着重要影响,在压气站中喘振控制系统的设计及相关设备的选型中应作为重点进行考虑。
(4) 该模型能够精确模拟压缩机的惰转过程,具有重要的现实意义。
| [1] | MOORE F K, GREITZER E M. A theory of post-stall transients in axial compression systems:Part Ⅰ-Development of equations[J]. ASME Journal of Engineering for Gas Turbines and Power, 1986, 108(1): 68-76. DOI: 10.1115/1.3239887 |
| [2] | ABED E H, HOUPT P K, HOSNY W M. Bifurcation analysis of surge and rotating stall in axial flow compressors[J]. Journal of Turbomachinery, 1993, 115(4): 817-824. DOI: 10.1115/1.2929320 |
| [3] | EVEKER K M, GYSLING D L, NETT C N, et al. Integrated control of rotating stall and surge in high-speed multistage compression systems[J]. Journal of Turbomachinery, 1998, 120(3): 440-445. DOI: 10.1115/1.2841735 |
| [4] | EPSTEIN A H, WILLIAMS J E F, GREITZER E M. Active suppression of aerodynamic instabilities in turbomachines[J]. Journal of Propulsion and Power, 1989, 5(2): 204-211. DOI: 10.2514/3.23137 |
| [5] | PADUANO J D, EPSTEIN A H, VALAVANI L, et al. Active control of rotating stall in a low-speed axial compressor[J]. Journal of Turbomachinery, 1993, 115(1): 48-56. DOI: 10.1115/1.2929217 |
| [6] | PADUANO J D, VALAVANI L, EPSTEIN A H, et al. Modeling for control of rotating stall[J]. Automatica, 1994, 30(9): 1357-1373. DOI: 10.1016/0005-1098(94)90001-9 |
| [7] | KURZ R, WHITE R C. Surge avoidance in gas compression systems[J]. Journal of Turbomachinery, 2004, 126(4): 501-506. DOI: 10.1115/1.1777577 |
| [8] | BOTROS K, BAKKER D. Application of three methods in determining the effectiveness of surge protection systems in gas compressor stations[C]//Proceedings of the 9th International Pipeline Conference. Calgary: ASME, 2012: 24-28. |
| [9] | BOTROS K, PETELA G. Use of method of characteristics & quasi-steady approach in transient simulation of compressor stations, advances in computational methods in fluid dynamics[C]//ASME Fluids Engineering Division Summer Meeting. Lake Tahoe, Nevada, USA, 1994. |
| [10] | ZHANG L. Simulation of the transient flow in a natural gas compression system using a high-order upwind scheme considering the real-gas behaviors[J]. Journal of Natural Gas Science and Engineering, 2016, 28: 479-490. DOI: 10.1016/j.jngse.2015.12.012 |
| [11] | PLETCHER R H, TANNEHILL J C, ANDERSON D A. Computational fluid mechanics and heat transfer[M]. 3rd ed. London: CRC Press, 2011. |
| [12] |
姬忠礼, 邓志安, 赵会军.
泵和压缩机[M]. 北京: 石油工业出版社, 2008.
JI Z L, DENG Z A, ZHAO H J. Pump and compressor[M]. Beijing: Petroleum Industry Press, 2008. |
| [13] |
段礼祥, 郝少鹏, 张北, 等. 基于ANSYS的往复压缩机国产活塞响应谱分析[J].
石油机械, 2017, 45(12): 62-66.
DUAN L X, HAO S P, ZHANG B, et al. Response spectrum analysis of the domestic piston of reciprocating compressor based on ANSYS[J]. China Petroleum Machinery, 2017, 45(12): 62-66. |



