0 引言
在进行水力压裂的储层改造过程中,人工裂缝经常会遭遇天然裂缝。因此,对人工裂缝与天然裂缝相交后裂缝的发育问题的研究就变得极为重要。当人工裂缝遭遇天然裂缝时,天然裂缝可能会发生剪切破坏、剪切滑移和剪切错断等现象,这些现象对人工裂缝能否穿过天然裂缝起着决定性作用。R.Q.JEFIFREY等[1]从定性的方向给出了天然裂缝对人工裂缝扩展的影响。文献[2-5]采用边界元法、扩展有限元法和离散元法等数值模拟方法分析了天然裂缝被破坏时的形态,但没有过多地分析天然裂缝的应力干扰作用,也没考虑力学参数对破坏天然裂缝形态的影响。T.L.BLANTON[6]的研究认为,人工裂缝和天然裂缝的逼近角和最大、最小主应力的大小是影响人工裂缝的主要因素。
以往的学者对分析天然裂缝的形态以及天然裂缝发生剪切破坏时的条件做作了详细研究,但对人工裂缝遭遇天然裂缝时能否穿过以及穿过所需要的条件却很少涉及。笔者在上述研究的基础上,建立了人工裂缝穿过天然裂缝的条件准则,推断出当人工裂缝穿过天然裂缝时,逼近角和最大最小主应力的比值需要满足的条件,并采用ABAQUS分析软件对人工裂缝穿过天然裂缝时所需要的条件进行了模拟分析。
1 人工裂缝与天然裂缝相交后裂缝走向 1.1 人工裂缝与天然裂缝相交时应力表达式裂缝性油藏在进行水力压裂的储层改造时,人工裂缝不断延伸,在延伸过程中,天然裂缝一定会经过天然裂缝发育区域,而天然裂缝的产状会对人工裂缝的发育和扩展起到决定性作用[7]。这时,控制裂缝的走向因素则变得复杂起来,此时,由地应力和水力压裂的压力因素变为了它们与天然裂缝共同控制的因素。想要人工裂缝穿过天然裂缝,则在人工裂缝与天然裂缝相交时,需要满足以下条件[8]:①作用在天然裂缝壁面上的正应力必须大于等于岩石的抗张强度。②天然裂缝不发生剪切滑移,如果发生剪切破坏,则需要继续持续加压以满足条件①。
假设在人工裂缝延伸的过程中只遭遇1条天然裂缝,人工裂缝与天然裂缝的逼近角为θ,最大最小主应力分别为σH和σh,天然裂缝与最大主应力方向的夹角为β,在最大最小主应力和天然裂缝的综合作用下,天然裂缝缝面上的应力表达式为[9]:
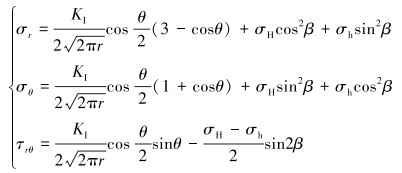
|
(1) |
式中:KI为I型应力强度因子,σr为径向应力,σθ为周向应力,τrθ为剪切应力,r为井眼半径。
设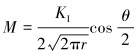
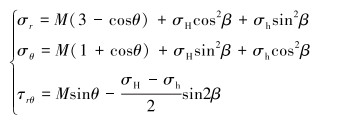
|
(2) |
在人工裂缝刚刚遭遇天然裂缝时,随着水力压裂的进行,如果想要人工裂缝穿过天然裂缝,需要满足一系列条件。设人工裂缝与天然裂缝相交处压力为σ1,天然壁面上正应力为σn,假设天然裂缝壁面上各处岩石力学性质相同。
1.2.1 当σ1≤σn时天然裂缝不发生剪切破裂时,则满足:
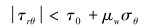
|
(3) |
式中:τ0为岩石黏聚力,裂缝闭合时为0;μw为天然裂缝面的内摩擦因数。
将式(2)代入式(3)并整理得:
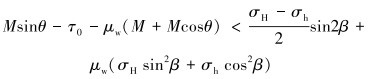
|
(4) |
当天然裂缝不发生剪切破裂时,裂缝的发育将有以下几种情况:
(1) 当天然裂缝另一边的壁面破裂压力高于天然裂缝的张开压力时,裂缝不发生延长。继续施加压力,一直到σ1>σn。
(2) 当天然裂缝另一边的壁面破裂压力低于天然裂缝的张开压力时,人工裂缝将穿过天然裂缝。此时的相交点压力σ′需满足:
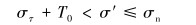
|
(5) |
式中:στ为平行天然裂缝缝面上的正应力;T0为岩石的抗张强度。
天然裂缝发生剪切破裂时,则满足:
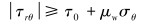
|
(6) |
整理式(6)可得:
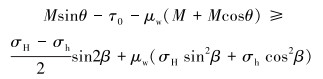
|
(7) |
此时的裂缝发生了剪切破坏,则裂缝的发育有2种情况。
(1) 裂缝暂时性的延伸停止,继续施加压力,一直到σ1>σn。
(2) 人工裂缝穿过天然裂缝。此时裂缝穿过需要满足的条件与天然裂缝不发生剪切时的第(2)种情况是相通的。
1.2.2 当σ1>σn时持续加压使得人工裂缝与天然裂缝相交处压力超过了天然壁面上的正压力,此时裂缝的发育有以下2种情况。
(1) 天然裂缝膨胀,人工裂缝沿着天然裂缝走向延伸,从天然裂缝的端部发生破裂而转向,继续沿着最小主应力的方向扩展;
(2) 天然裂缝膨胀,人工裂缝直接穿过天然裂缝。此时需满足:
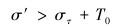
|
(8) |
除此条件之外,如果想要让人工裂缝直接穿过天然裂缝,还需满足条件:流体压力不能压开天然裂缝端部的同时又能压开交点处的另一侧壁面,因此需满足:
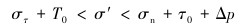
|
(9) |
式中:Δp为交点与最近端部之间流体的压力降。
整理式(9)可得:
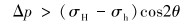
|
(10) |
综上所述,当天然裂缝未膨胀时,要想使人工裂缝穿过天然裂缝,必须满足式(4)和式(5),归纳为:
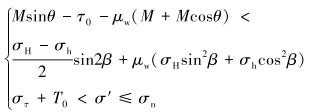
|
(11) |
当天然裂缝发生膨胀时,使人工裂缝穿过天然裂缝,必须满足式(8)和式(10),归纳为:
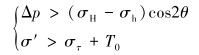
|
(12) |
设σH/σH=ε,分别代入式(11)和式(12)并整理得:
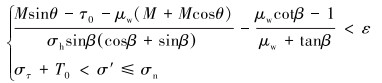
|
(13) |
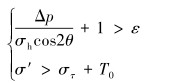
|
(14) |
式中的τ0、β、Δp、μw、T0、σH和KI这些数据在实际储层中都是固定且已知的,那么在进行水力压裂的过程中,当人工裂缝遭遇天然裂缝时,只有当最大最小主应力的比值ε和人工裂缝与天然裂缝的逼近角θ满足式(13)或式(14),人工裂缝才会穿过天然裂缝。
2 实例模拟验证 2.1 储层基本参数大庆某目标区块地层深度2 310 m,泊松比0.16,弹性模量5.3 GPa,孔隙度0.11,天然裂缝缝面内摩擦因数0.3,抗张强度5.3 MPa,缝内流体压力35 MPa,Boit系数0.6。人工裂缝与天然裂缝逼近角取5°、15°、30°、45°、60°和90°共6组,每组对应的最大最小主应力比取0.15、0.45、0.75、0.95、1.00、1.50、4.00和7.00共8组进行模拟。
2.2 ABAQUS软件模拟假设在人工裂缝延伸的过程中只遭遇1条天然裂缝,根据如下数据建立在人工裂缝刚刚与天然裂缝相交时的模型:井筒半径145.55 mm,人工裂缝长度20 m,天然裂缝长度15 m,裂缝缝宽4 mm。
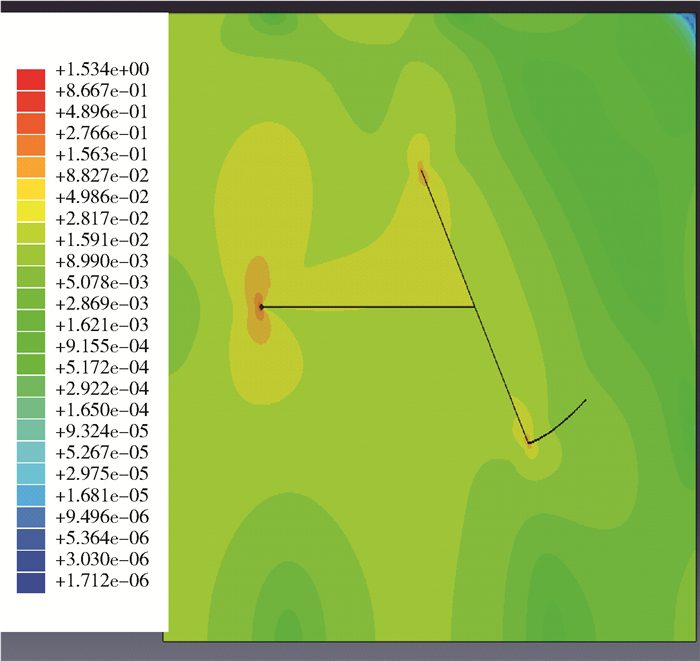
在进行结果显示时,如图 1所示代表人工裂缝穿过天然裂缝。如图 2所示代表人工裂缝没有穿过天然裂缝。图 1和图 2中的数值是对数变换显示结果,无量纲。

|
| 图 1 人工裂缝穿过天然裂缝情况 Fig.1 Artificial fracture crossing natural fracture |
|
| 图 2 人工裂缝未穿过天然裂缝情况 Fig.2 Artificial fracture not crossing natural fracture |
具体裂缝穿过情况如表 1所示(√表示人工裂缝穿过天然裂缝,×表示未穿过)。
| θ/(°) | 水平主应力比值 | |||||||
| 0.15 | 0.45 | 0.75 | 0.95 | 1.00 | 1.50 | 4.00 | 7.00 | |
| 5 | √ | √ | √ | √ | × | × | × | × |
| 15 | √ | √ | √ | √ | × | × | × | × |
| 30 | √ | √ | √ | √ | √ | × | × | × |
| 60 | × | √ | √ | √ | √ | √ | √ | √ |
| 90 | × | × | √ | √ | √ | √ | √ | √ |
从模拟结果可看出,最大最小主应力的比值和逼近角越大或最大最小主应力的比值与逼近角越小,人工裂缝越容易穿过天然裂缝。在确定了逼近角之后,存在当人工裂缝能够穿过天然裂缝时的最大最小主应力的一个比值范围,超过或小于该范围,人工裂缝都不会穿过天然裂缝。
3 结论(1) 基于人工裂缝遭遇天然裂缝时的应力场分析,建立了新的人工裂缝穿过天然裂缝时的判断准则,给出了能使人工裂缝穿过天然裂缝的最大最小主应力的比值与逼近角满足的关系式。
(2) ABAQUS模拟验证结果表明:在大庆油田特定区块的水力压裂过程中,最大主应力方向与人工裂缝方向垂直时,要想使人工裂缝遭遇天然裂缝时穿过天然裂缝,逼近角的范围必须在5°~30°之间;当最大主应力与人工裂缝方向一致时,要想使人工裂缝遭遇天然裂缝时穿过天然裂缝,逼近角的范围必须在60°~90°之间;当人工裂缝与天然裂缝垂直时,要想使人工裂缝遭遇天然裂缝时穿过天然裂缝,水平主应力比值必须大于0.75。模拟结果与理论推导结果一致。
(3) 水平主应力比值越高、逼近角越大或水平主应力比值越小、逼近角越小,人工裂缝越易穿过天然裂缝。
| [1] | JEFFREY R Q, ZHANG X, BUNGER A P. Hydraulic fracturing of naturally fractured reservoirs[C]//Proceedings of 35th Workshop on Geothermal Reservoir Engineering. Stanford, California: Stanford University, 2010. https://es.scribd.com/document/274607126/Hydraulic-Fracturing |
| [2] | THIERCELIN M, MAKKHYU E. Stress field in the vicinity of a natural fault activated by the propagation of an induced hydraulic fracture[R]. ARMA 07-201, 2007. http://www.mendeley.com/research/stress-field-vicinity-natural-fault-activated-propagation-induced-hydraulic-fracture/ |
| [3] | NAGEL N B, SANCHEZ-NAGEL M. Stress shadowing and microseismic events: A numerical evaluation[R]. SPE 147363, 2011. http://dx.doi.org/10.2118/147363-MS |
| [4] | KESHAVARZI R, MOHAMMADI S. A new approach for numerical modeling of hydraulic fracture propagation in naturally fractured reservoirs[R]. SPE 152509, 2012. |
| [5] | CHUPRAKOV D A, AKULICH A V, SIEBRITS E, et al. Hydraulic-fracture propagation in a naturally fractured reservoir[J]. SPE Production & Operations, 2011, 26(1): 88-97. |
| [6] | BLANTON T L. An experimental study of interaction between hydraulically induced and pre-existing fractures[R]. SPE 10847, 1982. http://dx.doi.org/10.2118/10847-MS |
| [7] |
李亚楠. 天然裂缝与人工裂缝相互作用机理及模型研究[D]. 大庆: 东北石油大学, 2016. LI Y N. Study on natural fracture and hydraulic fracture interaction mechanism and model[D]. Daqing: Northeast Petroleum University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10220-1016221041.htm |
| [8] |
赵金洲, 杨海, 李勇明, 等. 水力裂缝逼近时天然裂缝稳定性分析[J].
天然气地球科学, 2014, 25(3): 402-408.
ZHAO J Z, YANG M, LI Y M, et al. Stability of the natural fracture when the hydraulic fracture is approaching[J]. Natural Gas Geoscience, 2014, 25(3): 402-408. |
| [9] |
周健, 陈勉, 金衍, 等. 压裂中天然裂缝剪切破坏机制研究[J].
岩石力学与工程学报, 2008, 27(增刊1): 2637-2641.
ZHOU J, CHEN M, JIN Y, et al. Mechanism study of shearing slippage damage of natural fracture in hydraulic fracturing[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 2637-2641. |



