2. 中国科学院金属研究所
2. Institute of Metal Research, Chinese Academy of Sciences
0 引言
螺栓作为工业中常用的连接件,广泛应用于航空航天、船舶轮机、桥梁建设及石油化工设备等领域[1]。高强螺栓作为螺栓中的一种,具有强度高和承受高应力的特点。螺栓轴向应力或预紧力是影响螺栓性能、寿命以及使用状态的重要指标。在拧紧螺栓时若预紧力过大,易导致螺栓产生应力腐蚀裂纹和疲劳破坏;若预紧力不足则会引起振动松弛和滑移,影响结构整体性能或造成密封泄漏,这2种情况都将导致设备损坏和严重的事故发生。因此,应采取有效的手段控制高强螺栓的预紧力并监测螺栓的应力状态,以确保高强螺栓的使用安全。为控制和检测螺栓拧紧时的预紧力和工作状态下的应力状况,通常采用扭矩扳手法测量螺栓的预紧力。扭矩扳手法受摩擦系因数分散性和应力集中的影响存在较大误差,误差高达±40%[2]。为此,研发了超声波检测方法。超声法具有快速、简便和无损测量等优点,并且精度较高。超声波测量方法是根据声弹性原理,通过研究螺栓轴向应力与超声波传播时间(传播速度)的关系来测量螺栓中的应力。在拧紧的过程中,可根据回波信号把螺栓的预紧力调整到适当的范围[3]。超声法包含2种方法:纵波法和纵、横双波法。纵波法的优点是测量和标定操作简单,设备也简单,精确度高;缺点是必须测量螺栓不受力状态下的声波速度,已经上紧的螺栓需要松开,重新上紧。双波法的优点是无需测量螺栓不受力状态下的声波速度,已经上紧的螺栓不必松开;缺点是测量和标定操作复杂,设备也比较复杂,精确度低。双波法精度低的原因是横波不易耦合,耦合分散引起了较大误差,既影响标定,也影响测量,误差可达15%~25%[4]。为了克服耦合困难,有人采用了电磁超声(EMAT),EMAT不能在铁磁性介质中激励纵波,因此只适用于有色金属螺栓或奥氏体不锈钢螺栓[5]。国内外都在研究通过改进双波技术的标定方法提高测量精度[1-4],精度虽有所提高,但是整套技术的复杂程度不但未减,甚至增加,工业应用依旧困难。
为了建立快速简便的螺栓预紧力测量技术,笔者在介绍超声法测定螺栓应力原理的基础上,推导了超声波在螺栓两端传播的计算公式,依此建立了螺栓预应力指标计算模型,并对模型开展了现场试验。
1 超声法测定螺栓应力的原理超声波传播速度随应力状态改变而变化的现象称为声弹性现象。这种现象不论在弹性范围还是在非线性应力-应变范围均存在[6]。声弹性现象为超声应力测量技术提供了理论依据,以此为基础的材料应力测量方法称为声弹法。材料内部应力和应变之间的关系通常被认为是线性关系,即胡克定律。但是随着测量技术的发展,人们发现弹性模量等弹性常数不是不变的,而是随应变的大小不同而有微小的改变。当材料内部的原子通过压应力被压在一起时,弹性模量变大了,而当原子受拉应力被拉开时,弹性模量变小了,这表明应力和应变之间的关系是非线性的[7]。
对于各向同性弹性固体介质,在一维情况下,弹性体波(纵波和横波)的控制方程如下。
纵波控制方程:
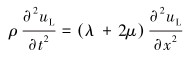
|
(1) |
横波控制方程:
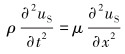
|
(2) |
进而可推导出纵波和横波声速计算公式。
纵波声速:
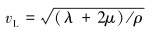
|
(3) |
横波声速:
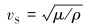
|
(4) |
式中:uL为纵波的位移,uS为横波的位移,t为时间,x为坐标轴,即x方向,λ和μ为各向同性体的2个Lame常数,ρ为材料密度。
当物体存在初始变形时,会出现2种可能:一种是初始变形与变形梯度很小,线性应力-应变关系仍然适用,那么所有的基本控制方程仍然是线性的。在线性弹性范围内,弹性波的传播与应力场无关,传播速度不会因应力的施加而改变。另一种情况是变形足够大,以至于线性应力-应变关系不再适用,应力-应变关系无法忽略高阶项。有高阶弹性时,弹性应变能U可以展开为应变ε的多项式[5]:
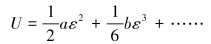
|
(5) |
这是一种非胡克应力-应变关系,式(5)对应变求导可得应力,即:
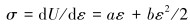
|
(6) |
式(6)中第1项是用二阶弹性常数a表示的线弹性;第2项代表的是线性度的偏差,用三阶弹性常数b来确定偏差的程度。
通过非胡克应力-应变关系可推出应变与弹性常数之间的关系, 弹性常数C可表示为:
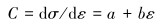
|
(7) |
假定介质中存在静应力σ0,考虑静应力对弹性常数的影响,因为弹性波的动应力σ很小,可以不考虑它对弹性常数的影响,于是有:
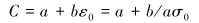
|
(8) |
波动方程仍按线弹性计算,弹性常数采用静应力σ0加以修正。纵波声速为:
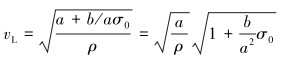
|
(9) |
当σ0=0时,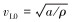
为了简化书写,下面用σ代替σ0, 即用σ代表静态应力,于是有:
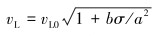
|
(10) |
将式(10)后面根号部分用Taylor级数展开,取前2项得:
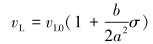
|
(11) |
采用同样的方法可推导出横波的声速计算公式,由于纵波声速与横液声速有同样的形式,所以都采用统一的形式,即有:
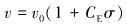
|
(12) |
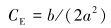
|
(13) |
v0是静应力为0时的速度,CE是速度的应力敏感因子。在这种近似范围内,弹性非线性导致了速度v对应力σ的线性依赖关系,试验结果表明,v-σ线性关系具有较高的精确性。
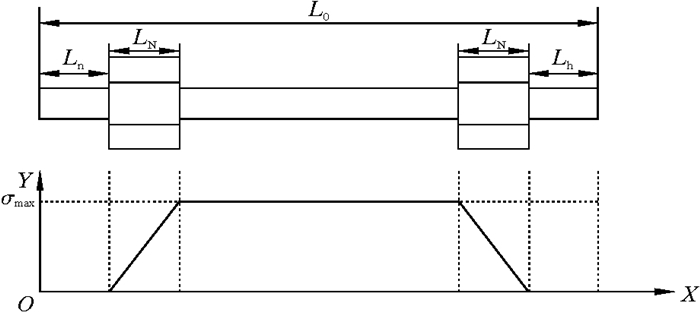
下面以图 1所示的简化模型为基础,计算螺栓的轴向应力。
|
| 图 1 高强螺栓拉应力轴向分布 Fig.1 Axial distribution of tensile stress of high-strength bolt |
螺栓的总长度为L0,在无应力条件下的体波速度为v0,LN和LH分别为两端螺母的高度。当沿轴向施加拉伸应力σ时,螺栓的一小段dx被拉长到(1+σ/E)dx的长度,E是弹性模量。螺栓受力后,纵波声速v随着应力变化而发生线性变化,如公式(12)所示。用上面的长度和速度计算超声波穿过该小段的时间dt,即有:
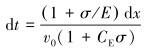
|
(14) |
由于σ/E=1、CEσ=1,忽略高次项之后, 上式可简化为:
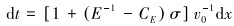
|
(15) |
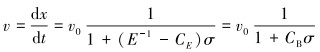
|
(16) |
这里CB=E-1-CE。在螺栓中往返1次的传播时间可表示为:
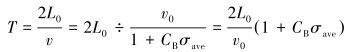
|
(17) |
令2L0/v0=T0,于是有:
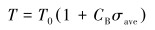
|
(18) |
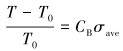
|
(19) |
这里L0表示螺栓未受力情况下的长度,σave=βσ,β为有效长度比。有效长度比β根据螺栓使用情况进行定义,对于图 1所示螺栓,β计算式为:
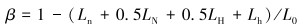
|
(20) |
图 1中L0=280 mm,LN=34 mm,LH=34 mm,Ln=42 mm,Lh=42 mm,计算得β=0.457 1。
2 超声法测定螺栓应力的试验公式(19)表明,只要在螺栓不受力和受力2种条件下测得超声波在螺栓两端面之间往返1次的时间,即公式中的T0和T,就可以计算出螺栓承受的应力σ。但是公式中的常数CB尚属未知,需要通过试验来求得,也就是通过试验来标定公式(19)中的线性关系。标定工作完成之后,就可以开展现场检测应用试验。
以压力容器常用的高强螺栓作为试样,对公式进行标定。螺栓材料为35CrMo钢,弹性模量209 GPa,屈服应力819 MPa,许用应力228 MPa[8]。螺栓长度280 mm,直径33 mm。螺帽高度34 mm。
超声波测量螺栓应力的试验装置由2部分组成:施加及测量应力部分和超声测量部分,整套装置如图 2所示。
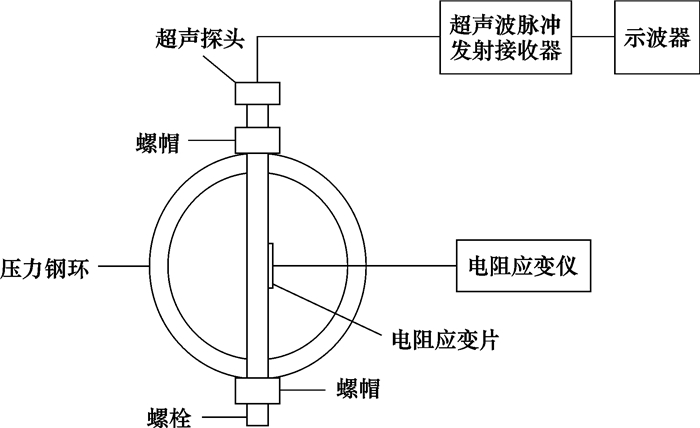
|
| 图 2 超声波测量螺栓应力示意图 Fig.2 Schematic diagram of ultrasonic measurement of bolt stress |
加力装置是一个厚壁圆环,最好用弹簧钢制作。钢环外径不超过200 mm,钢环上有2个ϕ35 mm的圆孔,2孔在圆周上相距180°,螺栓穿过2孔固定在圆环上,如图 3所示。扭紧螺帽可以对螺栓施加拉力。这种加力方式的优点是:①钢环-螺栓组装体的体积小、质量轻,可以携带到任何位置进行超声检测,也可以存放到任何时刻进行超声检测;②螺栓受力状况与螺栓使用状况相同;③结构简单,制作快,成本低。扭转螺母时须要较大的扭矩,因此必须将螺栓-钢环组装体固定在稳固的台架上。采用电阻应变片测量螺栓所受应力,笔者使用BFH120-3BA-Q3型120 Ω应变片和SDY2206型程控静态电阻应变仪,将应变换算成应力。

|
| 图 3 钢环-螺栓组装体 Fig.3 Steel ring-bolt assembly 1—超声探头;2—螺栓;3—螺帽;4—电阻应变片导线;5—固定装置;6—垫片;7—压力钢环。 |
测量超声波在螺栓两端面之间往返1次的传播时间,即测量公式(19)中的T和T0,使用2.5 MHz晶片,直径14 mm直探头,用OLYMPUS-5073型超声发射器和接收器来发射和接收超声波,用Tecktronix TDS-2012B型示波器显示回波并测量传播时间。实测的螺栓长度280 mm,再考虑测得的底波传播时间,由此算出超声波在未受力螺栓中的传播速度vL=5 921 m/s,这个速度与探伤手册给出的钢中纵波传播速度5 900~5 950 m/s符合。扭紧螺栓-钢环组装体上的螺母,对螺栓施加不同的拉力(拉力用应变片的应变测量),用上述方法测量传播时间,就得到了不同拉应力下T的数值。测量结果列于表 1中。
| 微应变 | 施加的应力/ MPa |
时间/ μs |
时间变化率/ 10-4 |
超声测量应力/ MPa |
| 0 | 0.000 | 94.571 9 | 0.000 | 0.000 0 |
| 57 | 11.913 | 94.581 1 | 0.973 | 16.640 7 |
| 110 | 22.990 | 94.587 6 | 1.660 | 28.397 7 |
| 153 | 31.977 | 94.590 0 | 1.914 | 32.738 8 |
| 191 | 39.919 | 94.598 8 | 2.844 | 48.656 0 |
| 220 | 45.980 | 94.600 7 | 3.045 | 52.092 6 |
| 296 | 61.864 | 94.607 2 | 3.733 | 63.849 7 |
| 349 | 72.941 | 94.608 4 | 3.859 | 66.020 2 |
| 380 | 79.420 | 94.610 5 | 4.082 | 69.818 6 |
对表中数据进行一元线性拟合,得到应力σ和传播时间变化率T-T0/T0之间的关系式和关系图,即公式(21)和图 4。习惯上称图 4的关系曲线为标定曲线。
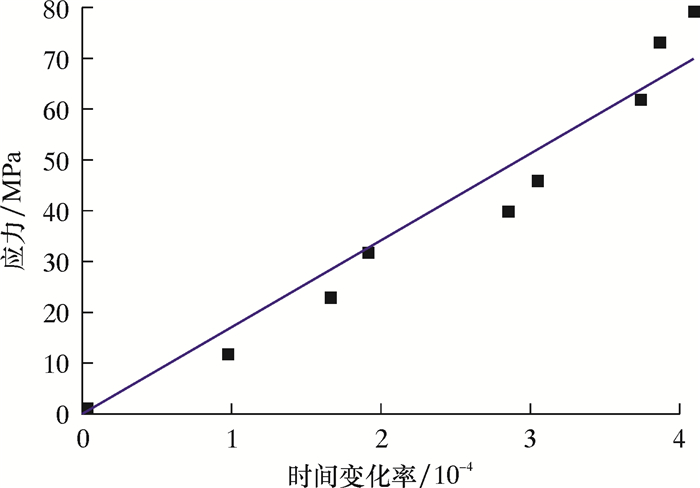
|
| 图 4 超声波纵波传播时间变化率与应力的关系曲线 Fig.4 The relation between the travel time change rate of ultrasonic longitudinal wave and stress |
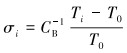
|
(21) |
根据线性回归法的原理,求常数即CB-1的方程为:
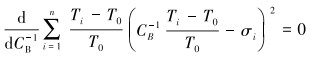
|
(22) |
于是有:
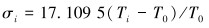
|
(23) |
超声测量的应力是σ,而应变片测量的应力是σs(施加的应力)。将应变片测量的应力视为真实应力,求出超声测量应力差值,如表 2所示。
| σs/MPa | σ/MPa | 应力差值/MPa | 差值平方/MPa2 |
| 0.000 | 0.000 0 | 0.000 0 | 0.000 0 |
| 11.913 | 16.640 7 | 4.727 7 | 22.351 2 |
| 22.990 | 28.397 7 | 5.407 7 | 29.243 2 |
| 31.977 | 32.738 8 | 0.761 8 | 0.580 3 |
| 39.919 | 48.656 0 | 8.737 0 | 76.335 2 |
| 45.980 | 52.092 6 | 6.112 6 | 37.363 9 |
| 61.864 | 63.849 7 | 1.985 7 | 3.943 0 |
| 72.941 | 66.020 2 | -6.920 8 | 47.897 5 |
| 79.420 | 69.818 6 | -9.601 4 | 92.186 9 |
由表 2中的差值平方计算超声测量应力的标准误差,即均方根误差:
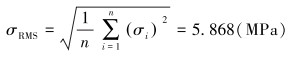
|
(24) |
公式(23)表明标定工作完成,可以进行现场螺栓应力的检测试验。条件是只能检测用35CrMo钢制作的各种规格的螺栓,其他螺栓的应力检测需要对相应的钢种重新制作标定曲线。对于新安装的设备,在螺母扭紧之前测出T0,扭紧过程中连续测量T,这样就能将螺栓的应力控制在标准规定的预紧力水平。在设备大修的过程中,如果设备已经泄压,可以和新安装设备一样控制螺栓的预紧力。如果不能泄压,可以选择多个螺栓中的一个,首先测量底波传播时间Ti,之后将螺母松开测量T0,最后重新扭紧螺母,在扭紧螺母的过程中连续测量T,将螺栓应力控制在设计的预紧力水平。从Ti可以计算旋松之前的螺栓预紧力。
3 讨论用表 2中的数据进行计算,可以得出螺栓应力测量的标准误差ΔσS=5.868 MPa,螺栓应力测量误差|Δσ|≤9.6 MPa的置信度为95%。误差的主要来源可能是螺栓受力的模型简化,因为应变的测量误差只有1%~3%,超声传播时间的测量误差是0.01 μs。
为了了解液体耦合分散性对超声传播时间测量的影响,在1根螺栓试样上进行了17次底波传播时间测量,得到的标准误差是ΔTS=0.013 6 μs。
相对于35CrMo钢螺栓的许用应力228 MPa,笔者的标定曲线最大应力只有80 MPa,因此有必要进一步测定应力范围更大的标定曲线。
4 结束语笔者开发的通过测量超声纵波传播速度测量螺栓预紧力的方法,在95%置信度的条件下测量误差≤10 MPa。使用小型便携式仪器,操作简便,在扭紧螺栓的过程中同时进行测量,每次测量所需时间不超过3 min。可以开展现场检测应用,并在应用中进一步考核。上述方法只是一项阶段性成果,有明显的局限性和缺点,表现在:①方法要求测量2次超声纵波在螺栓内的传播时间,一次在螺栓不受力的条件下进行,另一次在受预紧力或工作应力的条件下进行,进一步改进的方向是,只需要在受力条件下进行测量,在用螺栓不必松开就可以测量其所承受的应力;②标定应力的范围较小,只有80 MPa,有必要扩大到200 MPa以上;③误差仍然偏大,有必要进一步减小。
| [1] |
徐春广, 李骁, 潘勤学, 等. 螺栓拉应力超声无损检测方法[J].
应用声学, 2014, 33(2): 102-106.
XU C G, LI X, PAN Q X, et al. Bolt stress measurements by ultrasonic non-destructive methods[J]. Applied Acoustics, 2014, 33(2): 102-106. DOI: 10.11684/j.issn.1000-310X.2014.02.002 |
| [2] | JOHNSON Q C, HOLT A C, CUNNINGHAM B. An ultrasonic method for determining axial stress in bolts[J]. Journal of Testing and Evaluation, 1986, 14(5): 253-259. DOI: 10.1520/JTE10337J |
| [3] |
刘镇清, 王路. 用超声波技术测量螺栓轴向紧固应力[J].
测试技术学报, 1997, 11(1): 32-37.
LIU Z Q, WANG L. The measurement of axial stress in bolts by using ultrasonic technique[J]. Journal of Test and Measurement Technology, 1997, 11(1): 32-37. |
| [4] | CHAKIS, CORNELOUPG, LILLAMANDI, et al. Combination of longitudinal and transverse ultrasonic waves for in situ control of the tightening of bolts[J]. Journal of Pressure Vessel Technology, 2006, 129(3): 383-390. |
| [5] | HIRAOM, OGIH. Electromagnetic acoustic transducers: noncontacting ultrasonic measurements using EMATs[M]. 2nd ed. Japan: Springer, 2017: 233-269. |
| [6] |
王寅观. 声弹法及其应力测量的超声技术[J].
新技术新工艺, 1989(4): 13-15.
WANG Y G. Ultrasonic technology of acoustic bomb method and its stress measurement[J]. New Technology & New Process, 1989(4): 13-15. |
| [7] |
杜刚民, 李东风, 曹树林, 等. 螺栓轴向应力超声测量技术[J].
无损检测, 2006(1): 20-22, 25.
DU G M, LI D F, CAO S L, et al. Bolt axial stress measurement by ultrasonic testing[J]. Nondestructive Testing, 2006(1): 20-22, 25. |
| [8] |
秦晓钟, 滕明德.
世界压力容器用钢手册[M]. 北京: 机械工业出版社, 1995, 643-648.
QIN X Z, TENG M D. World handbook of steel for pressure vessels[M]. Beijing: China Machine Press, 1995, 643-648. |




