0 引言
修井机作为目前应用最广泛的石油特种车辆,对于石油与天然气开发重要性不言而喻[1-2]。由于修井作业连续工作时间长、作业强度大,司钻人员的不良作业姿态容易引发早期肌肉疲劳、关节酸痛甚至骨肌损伤。对司钻作业姿态舒适度进行研究,通过科学合理的操作舱人机布置,实现更为宜人的作业姿态,对延缓早期疲劳的产生、减少肌肉骨骼伤害(MSDs)有举足轻重的意义。
RULA(Rapid Upper Limb Assessment)[3]和REBA(Rapid Entire Body Assessment)[4]等作业姿态评价方法已经应用于很多领域,它们以关节角度作为评价依据,易用性好,但缺乏骨肌力学层面的分析数据支持,定量评价精确度不够,难以引导人机布置方案的优化。随着生物力学仿真技术的发展,利用AMS和OpenSim等仿真分析软件能够准确获得人体骨肌系统的力学参数,结合生理学相关研究,可以更为深入地了解人体疲劳特性[5]。对于司钻作业姿态定量评价来讲,考虑人体作业负荷,基于肌肉激活度的舒适度评价方法,显然更为准确、合理。
笔者将相关肌群的肌肉激活度作为舒适度评价指标,采用AMS对司钻作业下肢动作进行逆向动力学仿真,并运用Matlab对各肌群的仿真结果进行拟合处理;利用回归分析法确定相关肌群的权重系数,构建司钻作业姿态整体舒适度评价模型,从而实现操作舱布置设计方案的人机工效定量评价,并为其优化指明方向。
1 作业姿态设定及仿真模型构建 1.1 修井机司钻作业姿态设定自走式修井机的操作舱一般位于车辆尾部,受限于整车宽度及井架等上装设备的安装位置,舱体内部空间非常狭小却集中了大量显示仪表及控制装置,需要综合考虑司钻作业的可触及范围和视野范围等因素,因而人机布置难度较大。
修井机司钻人员的作业动作大致分为观察和操作2大类别,其中操作又可分为上肢动作和下肢动作,涉及工作刹车和油门控制等大量操纵装置,因此以用户为中心的作业动作规划就显得十分必要。笔者着重研究下肢油门踏板的操作动作,该动作属于典型的长时、高频操作,对坐姿下司钻作业舒适度影响很大,是操作舱人机布置的关键因素。
目前尚无修井机人机布置的行业标准,笔者结合修井作业要求[6]与SAE标准J1517中对B类车辆的相关规定[7],以司钻人员的乘坐参考点(SgRP)为基点,由坐高h、踵点水平距离l和座椅靠背倾角α 3个主要布置参数,共同确定了司钻人员工作姿态,如图 1所示。
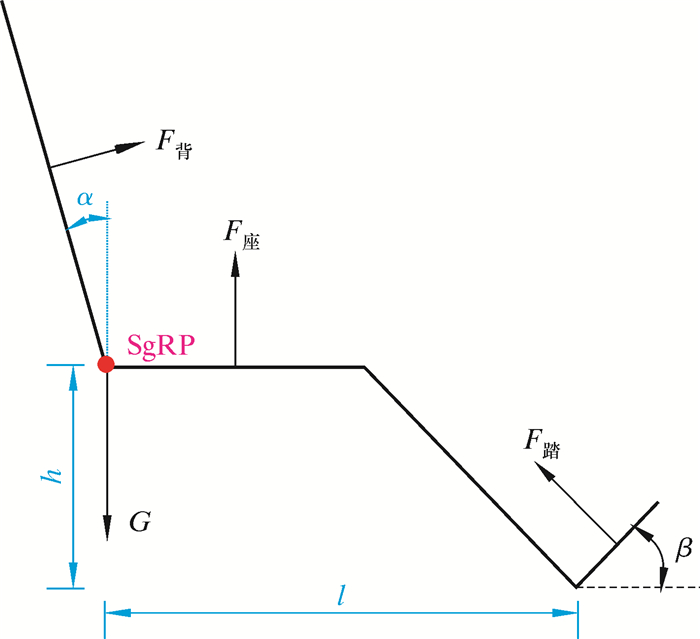
|
| 图 1 司钻人员主要布置参数及受力分析 Fig.1 The main layout parameters and force analysis of driller |
了解该作业姿态下司钻人员受力情况,可以更为准确地定义AMS仿真模型的约束及载荷;将人体躯干及下肢抽象简化为一个刚体模型,并对其进行受力分析,则力系平衡方程为:
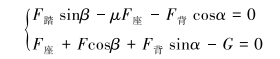
|
(1) |
计算得:
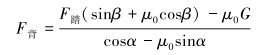
|
(2) |
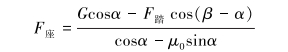
|
(3) |
式中:F背为靠背对人体的作用力,N;F座为座面对人体的作用力,N;F踏为踏板对人体的作用力,N;G为人体所受的重力,N;μ0为静摩擦因数;α为座椅靠背倾角,(°);β为脚踏板与地面的夹角,(°)。
1.2 逆向动力学仿真模型构建基于GB 10000—1988中国成年人人体尺寸数据,在AMS中建立了第50百分位中国成年男子人体骨肌模型,对其关节添加约束并调整数字人体模型的姿态,仿真模型如图 2所示。AMS的仿真参数设定如下:踏板旋转角度范围12°,运动时间0.5 s,阻力矩100 N·m/rad,座面的静摩擦因数0.3,踏板位置的横向和纵向变化范围设定为500 mm,步进值50 mm。
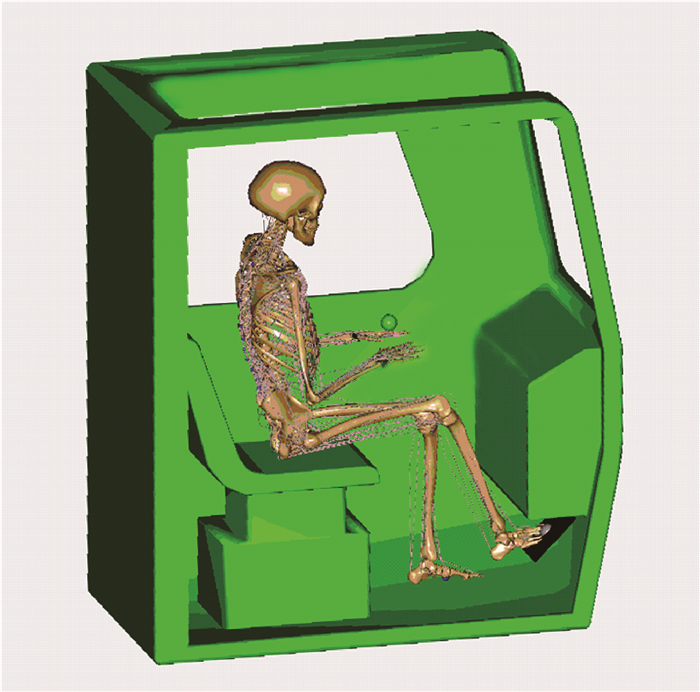
|
| 图 2 AMS逆向动力学仿真模型 Fig.2 AMS inverse dynamics simulation model |
为了解决逆向动力学求解中的肌肉冗余问题[8],根据肌肉激活度最优化原则构建目标函数:
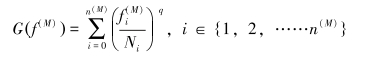
|
(4) |
式中:fi(M)为第i块肌肉的肌肉力,N;Ni为肌肉横截面积,mm2;n(M)为已知的肌肉总数。
考虑肌肉协同性因素,可以将多项式次数赋值为3。
2 仿真数据处理与分析踩下踏板的动作涉及下髋部、大腿、膝部、小腿、踝和足的几十个肌群,各肌群协同完成,但其贡献率差别巨大。笔者以运动解剖学结论为依据对参与肌群进行初步筛选[9],动作参与肌群如图 3所示。确定研究对象为臀中肌、臀大肌和大收肌等8组肌群,大大减少了数据处理量。利用AnyScript脚本语言提取仿真结果中选定的8组肌群激活度数值,以踏板位置为自变量,以相关肌群的肌肉激活度为因变量,运用Matlab软件构建各肌群对应的舒适度评价模型[10];再利用回归分析法,多次迭代确定参与肌群对整体舒适度评价的影响权重,进而构建整体舒适度评价模型,具体流程如图 4所示。

|
| 图 3 动作参与肌群示意图 Fig.3 Schematic diagram of muscle groups involved in action 1—臀中肌;2—臀大肌;3—大收肌;4—半腱肌;5—半膜肌;6—股二头肌;7—肌四头肌。 |
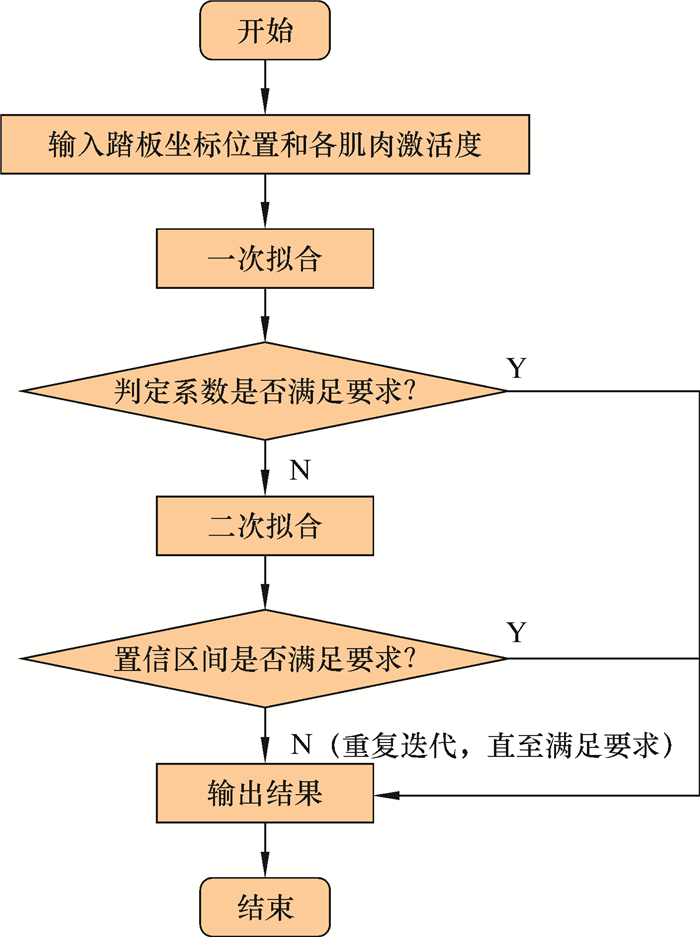
|
| 图 4 回归分析法流程图 Fig.4 Regression analysis flowchart |
2.1 相关肌群的舒适度评价模型
在AMS中,脚踏位置参数以50 mm为步进值在500 mm范围内变化;从仿真结果中提取大收肌的肌肉激活度,图 5为其散点图,图中水平坐标(x, y)为脚踏位置,垂直坐标P为肌肉激活度。
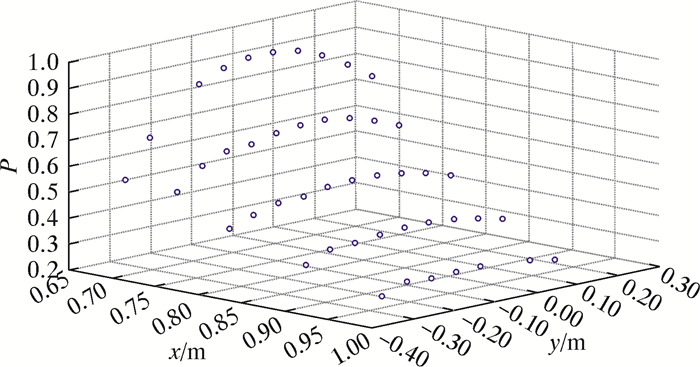
|
| 图 5 大收肌激活度散点图 Fig.5 Scattering diagram of the adductor magnus activity |
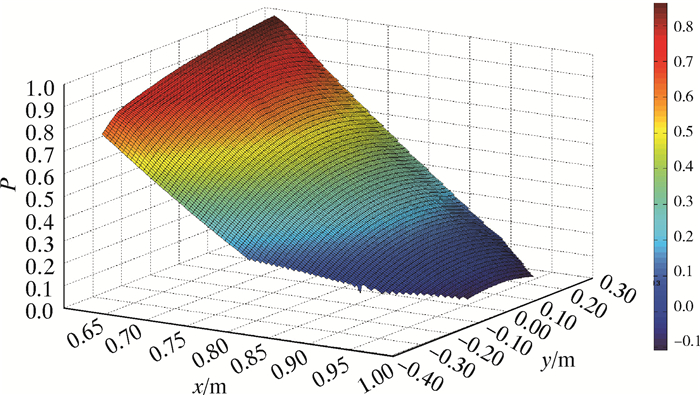
以脚踏位置(x, y)为自变量,大收肌肌肉激活度P1为因变量,构建其姿态舒适度评价模型P1=f1(x, y);利用Matlab将仿真结果二次拟合,得到如图 6所示曲面,其函数表达式为:
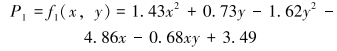
|
(5) |
|
| 图 6 大收肌激活度二次拟合图 Fig.6 Quadratic fit diagram of the adductor magnus activity |
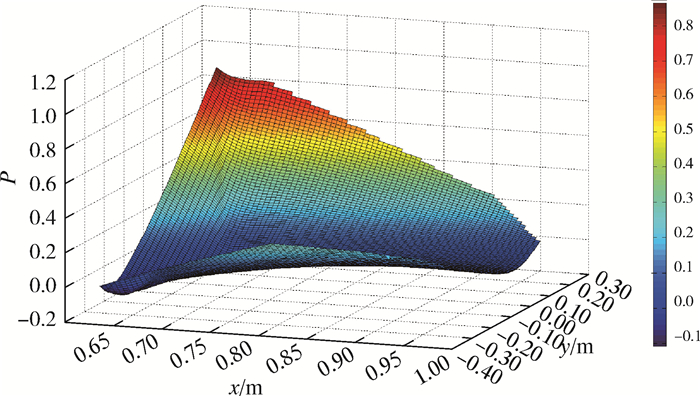
同理,可得到股二头肌激活度二次拟合图,如图 7所示,其函数表达式为:
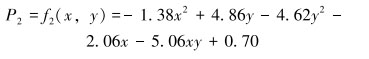
|
(6) |
|
| 图 7 股二头肌激活度二次拟合图 Fig.7 Quadratic fit diagram of the biceps femoris activity |
依次得到肌群激活度二次拟合图,臀大肌评价模型的函数表达式为:
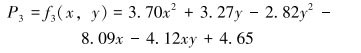
|
(7) |
臀中肌评价模型的函数表达式为:
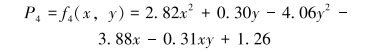
|
(8) |
股四头肌评价模型的函数表达式为:
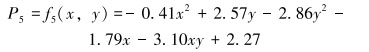
|
(9) |
半膜肌评价模型的函数表达式为:
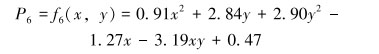
|
(10) |
半腱肌评价模型的函数表达式为:
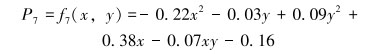
|
(11) |
阔筋膜张肌评价模型的函数表达式为:
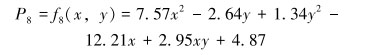
|
(12) |
首先,等权重下整体舒适度评价模型为:
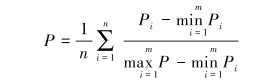
|
(13) |
式中:P为整体舒适度;i为变量代号;n为自变量个数;m 为数据记录个数;Pi为各肌群激活度。
等权重下各肌群舒适度与整体舒适度的相关关系如表 1所示,分别为0.860、0.630、0.830、0.110、0.770、0.540、0.004和0.110。
| 关系项 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P |
| P1 | 1.000 | 0.300 | 0.840 | -0.210 | 0.870 | 0.210 | -0.100 | -0.040 | 0.860 |
| P2 | 0.300 | 1.000 | 0.280 | 0.220 | 0.290 | 0.800 | 0.340 | -0.270 | 0.630 |
| P3 | 0.840 | 0.280 | 1.000 | -0.260 | 0.880 | 0.200 | -0.140 | -0.080 | 0.830 |
| P4 | -0.210 | 0.220 | -0.260 | 1.000 | -0.490 | 0.290 | 0.090 | 0.520 | 0.110 |
| P5 | 0.870 | 0.290 | 0.880 | -0.490 | 1.000 | 0.220 | -0.100 | -0.260 | 0.770 |
| P6 | 0.210 | 0.800 | 0.200 | 0.290 | 0.220 | 1.000 | 0.310 | -0.180 | 0.540 |
| P7 | -0.100 | 0.340 | -0.140 | 0.090 | -0.100 | 0.310 | 1.000 | -0.230 | 0.004 |
| P8 | -0.040 | -0.270 | -0.080 | 0.520 | -0.260 | -0.180 | -0.230 | 1.000 | 0.110 |
| P | 0.860 | 0.630 | 0.830 | 0.110 | 0.770 | 0.540 | 0.004 | 0.110 | 1.000 |
对相关系数进行归一化处理,得到各肌群与整体舒适度之间的不等权重系数,分别为0.220、0.160、0.220、0.030、0.200、0.140、0.001和0.028;将各肌群评价模型的函数表达式带入,即得到踏板位置与整体舒适度之间的函数表达式:
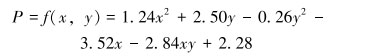
|
(14) |
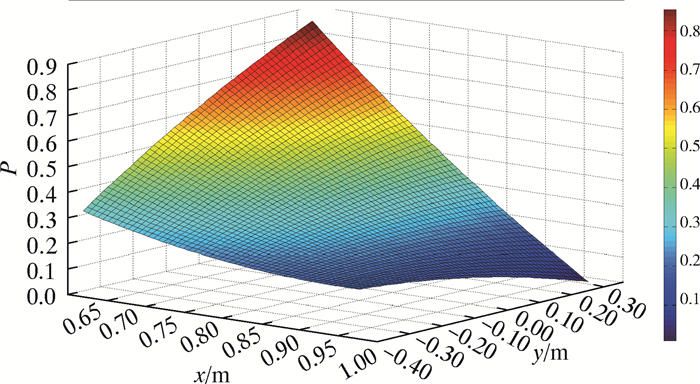
整体舒适度二次拟合图如图 8所示。
|
| 图 8 整体舒适度二次拟合图 Fig.8 Quadratic fit diagram of the overall comfort level |
从整体舒适度模型可以看出,踏板位置参数是操作舱人机布置优化的关键。伴随踏板位置逐渐远离人体冠状面,下肢肌肉激活度整体呈现下降趋势;伴随踏板位置逐渐远离人体矢状面,下肢肌肉激活度整体呈现下降趋势。相对来讲,踏板位置在冠状面附近时,适当远离近身范围整体舒适度提升幅度超过80%;踏板位置在矢状面附近时,适当远离近身范围整体舒适度也会有50%左右的提升;踏板位置在接近下肢可触及范围的边缘时,整体舒适度会有小幅度降低。使用该整体舒适度评价模型,可以非常快捷、准确地筛选操作舱布局设计方案,也可为座椅调节范围等参数设定提供依据。
3 结束语与目前主流的基于关节角度的姿态评价方法相比,基于肌肉激活度的作业姿态舒适度评价,考虑了人体疲劳特性及多肌群协同对整体舒适度的影响,可以更为准确地对操作舱设计方案进行人机工效评价,并为其人机布置优化指引方向。由于笔者只研究了踏板位置参数对下肢整体舒适度的影响,后续研究可考虑增加坐高、靠背倾角等布置参数和上肢操作的仿真。
| [1] |
谢永金. 我国修井机发展的技术现状与展望[J].
石油机械, 2005, 33(10): 72-75.
XIE Y J. Technical status and prospects of workover rig development in China[J]. China Petroleum Machinery, 2005, 33(10): 72-75. DOI: 10.3969/j.issn.1001-4578.2005.10.027 |
| [2] |
冯定, 杨志远, 柳进, 等. 液压修井机现状与发展趋势[J].
石油机械, 2010, 38(1): 69-72.
FENG D, YANG Z Y, LIU J, et al. Status and development trend of hydraulic workover rigs[J]. China Petroleum Machinery, 2010, 38(1): 69-72. |
| [3] | MC ATAMNEY L, CORLETT E N. RULA:a survey method for the investigation of work-related upper limb disorders[J]. Applied Ergonomics, 1993, 24(2): 92-98. |
| [4] | HIGNETT S, MC ATAMNEY L. Rapid entire body assessment(REBA)[J]. Applied Ergonomics, 2000, 31(2): 202-204. |
| [5] |
丁晨, 王君泽, 高瞻. 基于AnyBody的汽车驾驶中人体腿部逆向动力学仿真[J].
中国生物医学工程学报, 2013, 32(1): 125-126.
DING C, WANG J Z, GAO Z. Inverse dynamics simulation of the musculoskeletal model of human legs in driving based on AnyBody modeling system[J]. Chinese Journal of Biomedical Engineering, 2013, 32(1): 124-128. |
| [6] |
束奇, 王丙刚. 基于CATIA的修井机作业操控室人机工程设计[J].
人类工效学, 2012, 18(3): 49-53, 57.
SHU Q, WANG B G. Ergonomic design of operation control cabin of workover rig based on CATIA[J]. Chinese Journal of Ergonomics, 2012, 18(3): 49-53, 57. |
| [7] |
任金东.
汽车人机工程学[M]. 北京: 北京大学出版社, 2010, 142-159.
REN J D. Automotive ergonomics[M]. Beijing: Peking University Press, 2010, 142-159. |
| [8] | DINESH K P. Muscle mass in musculoskeletal models[J]. Journal of Biomechanics, 2010, 43(11): 2094-2097. |
| [9] |
布朗蒂娜﹒卡莱-热尔曼. 运动解剖书: 运动者最终要读透的身体技能解析书[M]. 北京: 北京科学技术出版社, 2015: 227-254. CALLE-GERMAN B. Anatomie pour le mouvement[M]. ZHANG F, trans. Beijing: Beijing Science and Technology Press, 2015: 227-254. |
| [10] | LI W H, ZHANG M, LV G M, et al. Biomechanical response of the musculoskeletal system to whole body vibration using a seated driver model[J]. International Journal of Industrial Ergonomics, 2015, 45: 91-97. DOI: 10.1016/j.ergon.2014.12.006 |



