2. 江苏省特种设备安全监督检验研究院
2. Special Equipment Safety Supervision Inspection Institute of Jiangsu Province
0 引言
多孔介质是一种由固体骨架和孔隙空间构成的多相物质,应用于阻隔防爆和强化传热的多孔介质必须是开孔结构的多孔介质,即孔隙之间相互连通[1]。由于多孔材料具有比表面积大、质量轻、体积小以及导热性能好等优点,所以多孔材料越来越被人们所关注。它广泛用于工业、国防科技和环境保护等领域,可作为防火防爆填充材料及噪声环境下的吸声材料等。多孔材料作为填充材料,常常是填充在密闭容器和管道等内提高其阻隔防爆及强化传热等特性。D.A.NIELD等[2]最先开始多孔介质方面的研究。H.SHOKOUHMAND等[3]讨论了多孔材料放置位置对通道流动及传热的影响。M.E.NIMVARI等[4]研究了通道中心和壁面2种位置放置多孔材料,通道内湍流流动和传热的变化情况。关于储罐内填充多孔材料的研究相对较少,邢志祥等[5]模拟了圆柱形储罐内填充聚氨酯多孔材料后可燃气体火焰传播的情况,并对比了13L圆柱形密闭储罐现场试验结果,研究结果表明:模拟结果与试验结果相吻合,填充物平均孔径越小,阻火抑爆性能越好;田宏等[6-7]只是对填充在液化石油气储罐中的多孔金属材料做了笼统介绍,并没有通过试验来验证。
液化天然气(LNG)储罐是储存液化天然气的重要设备,其运行时处于超低温状态下容易引发各类安全事故,液化天然气翻滚是其中一种类型。储罐内由于LNG存在密度差而产生分层,在上层液体和下层液体之间产生一层薄薄的液-液分界面,外界环境和储罐内液体存在温度差而导致热量通过壁面向液体传递,储罐壁面处的流体率先吸收热量导致密度减小,产生浮力驱动流,沿着壁面向上移动,形成流动边界层;由于上、下2层流体存在温度差和密度差,所以位于分界面处的流体出现自然对流现象,且流体流速较储罐其他位置的流速大,而分界面处边界层的流体流速最大。当上层液体和下层液体密度接近一致时,下层液体会突然越过上层液体,急剧蒸发,产生大量蒸发气体,安全阀频繁开启,释放到大气空间,更加严重的还会发生爆炸,造成严重的经济损失和安全生产事故。基于多孔材料的优点,笔者选取储罐边界层填充多孔材料,并取不同的填充厚度(1.0、1.5和2.0 mm),通过建立储罐边界层填充多孔材料的物理模型与数学模型,对储罐内液体的流动情况进行数值模拟,以期为储罐内填充多孔材料抑制LNG翻滚事故的发生提供理论指导。
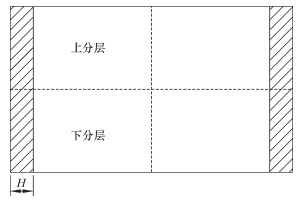
1 多孔材料填充储罐内液体流动计算模型的建立 1.1 物理模型对边界层填充多孔材料进行模拟,建立的物理模型如图 1所示。
|
| 图 1 在储罐边界层填充多孔材料的物理模型 Fig.1 Physical model for filling the porous material in the boundary layer of the storage tank |
对填充多孔材料储罐内液化天然气流动情况的物理模型(灰色区域为多孔材料区域,白色区域为纯流体区域)做如下简化:①储罐内部流体分成2个高度相等的分层,上分层流体密度为424 kg/m3,下分层流体密度为425 kg/m3,初始密度差为1 kg/m3,2个分层内的密度均匀一致;②储罐内流体密度符合Boussinesq假设;③选取金属铝多孔材料,且视多孔材料为均匀各向同性;④多孔材料的孔隙为球形空洞,孔隙之间相互连通,即为开孔结构;⑤多孔材料的物性参数为常数;⑥多孔材料固体骨架与流体处于局部热平衡,且无任何化学反应;⑦储罐内流体流动为湍流流动;⑧忽略流体流动过程中的黏性耗散;⑨不考虑辐射换热。
1.2 数学模型采用非稳态模型、VOF模型和标准k-ε湍流模型,基于Boussinesq假设,多孔区域动量方程采用Darcy-Brinkman-Forchheimer模型,能量方程采用局部热平衡模型,得到的控制方程如下。
连续性方程:
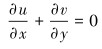
|
(1) |
式中:u为x轴方向的速度分量,m/s;v为y轴方向的速度分量,m/s。
动量方程:
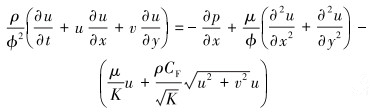
|
(2) |
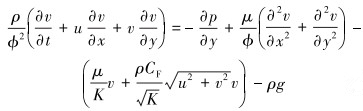
|
(3) |
式中:ρ为液体密度,kg/m3;t为时间,s;p为压力,Pa;μ为动力黏度,Pa·s;g为重力加速度,m/s2;φ为孔隙率;K为渗透率,m2;CF为Forchheimer系数。
能量方程:
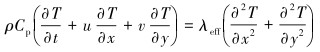
|
(4) |
式中:Cp为定压比热容,J/(kg·K);T为温度,K;λeff为多孔区域的有效导热系数,W/(m·K)。
k方程:
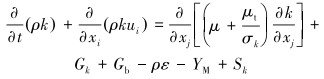
|
(5) |
ε方程:
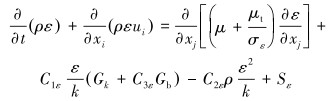
|
(6) |
式中:k、ε分别为湍动能和湍流扩散率;σk、σε分别为k方程和ε方程的普朗特数,σk= 1.0,σε= 1.3;μt为湍流黏性系数,μt =Cμρk2/ε,其中Cμ =0.09;Gk为平均速度梯度引起的湍动能k的产生项;Gb为浮力引起的湍动能k的产生项;YM为可压缩湍流流动中脉动扩张的贡献;C1ε、C2ε、C3ε为经验常数,C1ε =1.44,C2ε =1.92,C3ε =1;Sk、Sε为用户自定义源项。
当φ= 1时,k→∞,λeff =λf,动量方程的源项趋近于0,能量方程也变为标准能量方程,则上述控制方程变为纯流体区域的控制方程。多孔区域的有效导热系数λeff由流体的导热系数λf和固体的导热系数λs的体积平均值计算得到,即λeff = (1-φ)λs+φλf。在计算过程中,多孔区域和纯流体区域通过φ的取值进行区分,统一进行求解。
1.3 边界条件和初始条件储罐侧壁面和底壁面取为无滑移壁面边界条件,并采用定热流的方式加热,热流密度恒定为30 W/m2;气液交界面取为压力出口;多孔区域采用金属铝多孔材料,孔隙率设为0.95,并需设定黏性阻力系数和惯性阻力系数;多孔区域与纯流体区域的交界面设为内部边界。
初始表压为15 kPa,x和y轴方向的速度分量都为0,分层区初始温度为111.0 K,主流区初始温度为111.5 K。
1.4 相关参数介绍 1.4.1 孔隙率和孔径[8]孔隙率φ是指孔隙体积占多孔材料总体积的比值;孔密度n是指多孔材料每英寸上孔的数目,孔径dp = 0.025 4 m。
1.4.2 渗透率K和Forchheimer系数[9]渗透率K代表了多孔介质中孔隙的表面积和弯曲程度,通常由Vafai总结的经验公式确定:
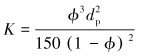
|
(7) |
当多孔材料中的流体流动为湍流流动时,达西定律便不能描述流体流动的情况,此时可采用其修正模型进行描述,即在动量方程中加入源项,源项由黏性阻力项和惯性阻力项组成,惯性阻力项的系数用CF表示,称为Forchheimer系数,表示为:
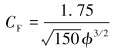
|
(8) |
压差Δp=p2-p1,其中p2为底壁面平均压力,p1为压力出口平均压力。
2 结果分析 2.1 储罐内无多孔材料填充的液化天然气流动情况储罐内液体翻滚的发生需要孕育时间和计算机的限制,因此在对填充多孔材料后储罐内液体的流动情况进行模拟时,并没有对整个过程进行模拟,只进行了前1 000 s时的计算及分析。无多孔材料填充时的模拟结果如图 2所示。
|
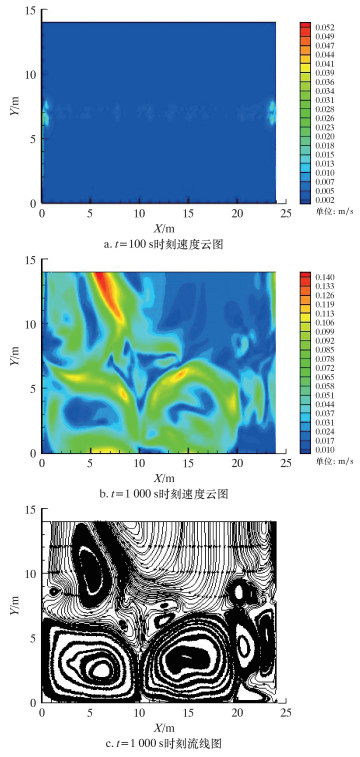
| 图 2 无多孔材料填充时t=100和t=1 000 s 时刻的模拟结果 Fig.2 Simulation results at time t=100 and t=1 000 s without porous material filling |
从图 2可以看出,在t=100 s时,由于外界环境的漏热,储罐壁面处的流体率先吸收热量导致密度减小,产生浮力驱动流,沿着壁面向上移动,形成流动边界层;由于上、下2层流体存在温度差和密度差,所以位于分界面处的流体出现自然对流现象,且流体流速较储罐其他位置的流速大,而分界面处边界层的流体流速最大;此刻,储罐内流速最大为0.04 m/s。在t=1 000 s,分界面处流体的自然对流发展到整个储罐内流体的自然对流,且上、下2层流体的自然对流各自独立,即由液液分界面隔开,被限制在自身区域内;对于上层流体,由于储罐侧壁面的漏热,导致边界层处的流体受热膨胀密度减小,沿储罐壁面向上移动,当其到达气液交界面时,其中一部分流体蒸发变成气体释放到气相空间,其密度增大导致向下移动,由此形成了上层流体的自然能对流现象;对于下层流体,边界层处的流体受热膨胀密度减小,沿着边界层向上移动,当其到达液液分界面时,因浮力太小而无法穿过分界面进入上层,但会通过分界面向上层流体传递热量,因而温度降低,密度增大,导致向下移动,由此形成了下层流体的自然能对流现象。
在纯自然对流运动中,瑞利数Ra是判定由浮力产生的对流强度大小的标准[10]。当瑞利数Ra小于临界值时,流体之间是热传导状态,不发生对流运动;当瑞利数Ra大于临界值时,才会发生对流运动,从而在液体中出现宏观对流花纹,称其为Benard花纹[11]。储罐内无多孔材料填充时,在t=1 000 s时,上层和下层的自然对流结构明显不同,但流动都是由类似圆形的滚动圈组成,上层的滚动圈数为1个,为扁长形,而下层的滚动圈数为4个,分别为2个胖圆形和2个扁长形的滚动圈;相比于t=100 s时分界面处的流体流速较高,t=1 000 s时分界面处的流体流速反而较小,除此之外,在滚动圈中心处的流速也较小,称为滞留区。
储罐内无多孔材料填充时,二维截面上的最大流速为0.195 m/s。
2.2 多孔材料填充厚度H为1.0 m时的液化天然气流动情况多孔材料填充厚度为1.0 m时的模拟结果如图 3所示。
|
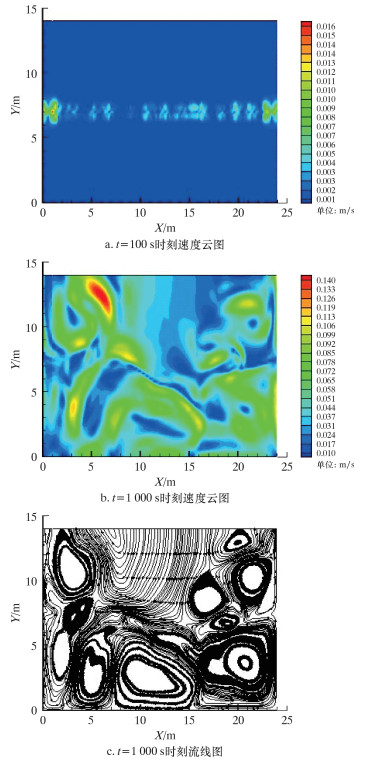
| 图 3 多孔材料填充厚度为1.0 m时,t=100和t=1 000 s 时刻的模拟结果 Fig.3 Simulation results at time t=100 and t=1 000 s with the filled porous material thickness of 1.0 m |
从图 3可以看出,在t=100 s时,储罐内最大流速为0.015 m/s,而无多孔材料填充时储罐内最大流速为0.040 m/s;在分界面两侧对流强度较高,且以多孔材料与流体区域交界面为中心,形成了“翅膀形”对流图案,且多孔区域对流范围小于纯流体区域对流范围。在t=1 000 s时,储罐内最大流速为0.148 m/s,多孔材料填充区域比相邻区域的流体流速小,且滚动圈没有穿过多孔材料,而是沿着多孔材料与流体区域交界面滚动;从流线图中可以看出,相比于不填充多孔材料时而言,上层和下层的自然对流结构有明显不同,上层的自然对流结构由1个扁长形滚动圈变为几个小的椭圆形滚动圈;下层的自然对流结构由2个胖圆形和2个扁长形的滚动圈组成,只是滚动圈比无多孔材料填充时的小,滚动圈方向从左到右依次为顺时针、逆时针、顺时针、逆时针和顺逆方向是交替出现;同时发现,罐体两边的流动强度较弱,中间的流动强度较强。
储罐内沿边界层填充多孔材料厚度为1.0 m时,二维截面上的最大流速为0.184 m/s。
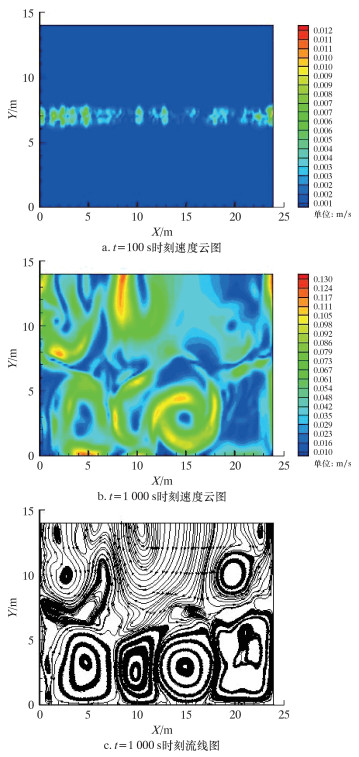
2.3 多孔材料填充厚度H为1.5 m时的液化天然气流动情况多孔材料填充厚度为1.5 m时的模拟结果如图 4所示。从图可以看出,在t=100 s时,储罐内最大流速为0.013 m/s,仍是边界层处流体和分界面处流体的流速较储罐其他位置的流速大,分界面处出现自然对流现象。在t=1 000 s时,储罐内最大流速为0.129 m/s。从流线图可以看出,上层的自然对流结构和多孔材料填充厚度为1.0 m时明显不同,滚动圈明显变小,下层的自然对流结构沿储罐中心线呈对称分布,由4个大小近似相等的胖圆形滚动圈组成,从左到右的滚动圈方向依次为顺时针、逆时针、顺时针和逆时针,与多孔材料填充厚度为1.0 m时的滚动圈方向一致。从速度云图上可以看出,在壁面热边界条件和多孔材料作用下,罐体两边流动强度较弱,中间流动强度较强,两侧滚动圈的滞留区面积比中间滚动圈大。
|
| 图 4 多孔材料填充厚度为1.5 m时,t=100 s 和t=1 000 s 时刻的模拟结果 Fig.4 Simulation results at time t = 100 and t = 1 000 s with the filled porous material thickness of 1.5 m |
储罐内沿边界层填充多孔材料厚度为1.5 m时,二维截面上的最大流速为0.163 m/s。
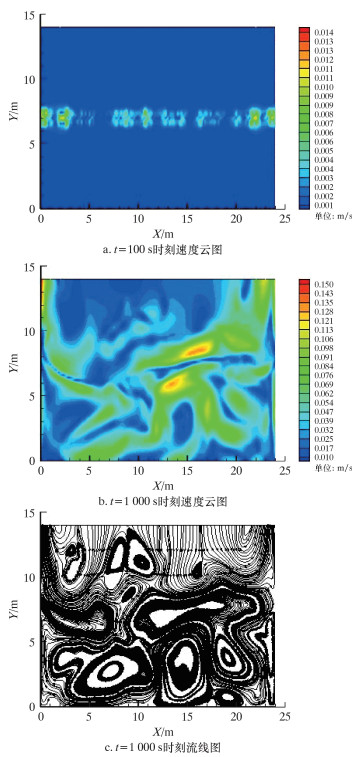
2.4 多孔材料填充厚度H为2.0 m时的液化天然气流动情况多孔材料填充厚度为2.0 m时的模拟结果如图 5所示。
|
| 图 5 多孔材料填充厚度为2.0 m 时,t=100和t=1 000 s 时刻的模拟结果 Fig.5 Simulation results at time t=100 and t=1 000 s with the filled porous material thickness of 2.0 m |
从图 5可以看出,在t=100 s时,储罐内最大流速为0.014 3 m/s,储罐内流体流动发展情况和同时期多孔材料填充厚度为1.5 m时比较相似,都是在多孔材料填充区域与壁面接触一侧流速较高,与液体接触一侧流速较低;在t=1 000 s时,储罐内最大流速为0.150 m/s,对流运动的高速区域明显比无多孔材料填充及多孔材料填充厚度为1.0和1.5 m时的小;从流线图可以看出,在中间界面出现了2个扁长形滚动圈,下层的自然对流结构为3个较大的胖圆形滚动圈和1个扁长形滚动圈,且与多孔材料填充厚度为1.0和1.5 m时的滚动圈方向一致,同时从速度云图可以看出,在壁面热边界条件和多孔材料作用下,同样也是罐体两边的流动强度较弱,中间的流动强度较强,两侧滚动圈的滞留区面积比中间滚动圈大。
储罐内沿边界层填充多孔材料厚度为2.0 m时,二维截面上的最大流速为0.181 m/s。
2.5 多孔材料填充厚度对液化天然气流动情况影响分析不同多孔材料填充厚度下的二维截面最大平均流速如表 1所示。从表可以看出,填充多孔材料可降低流体的平均流速,且填充厚度越厚,流体的平均流速越低。
| 填充厚度/m | 0.0 | 1.0 | 1.5 | 2.0 |
| 最大平均流速/ (m·s-1) | 0.052 8 | 0.051 1 | 0.049 1 | 0.048 9 |
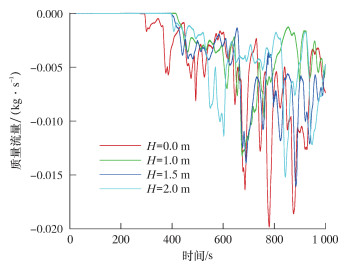
图 6是不同多孔材料填充厚度下的压力出口质量流量变化曲线图。在气液交界面有蒸发气体进入到气相空间,气相空间压力增大,当其超过安全阀设定压力时,安全阀开启,释放蒸发气体到大气空间,当储罐内液体发生翻滚时,会瞬间产生大量蒸发气体,不仅会带来经济损失,还会发生安全事故。从图 6可以看出,不管是哪种情况,压力出口的质量流量都为负值,但填充多孔材料的储罐均能不同程度地减少压力出口质量流量,这样不仅可减少经济损失,还可减弱事故发生时的剧烈程度,起到一定的抑制作用;此外,填充多孔材料的储罐均能延迟压力出口有蒸发气体流出的时间。
|
| 图 6 不同多孔材料填充厚度下的压力出口质量流量变化曲线图 Fig.6 Pressure outlet mass flow under different thicknesses of porous materials |
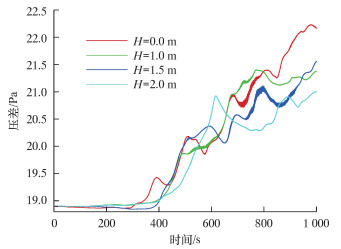
图 7是不同多孔材料填充厚度下的压差变化曲线图。
|
| 图 7 不同多孔材料填充厚度下的压差变化曲线 Fig.7 Pressure differences under different thicknesses of porous materials |
从图 7可以看出,在储罐内填充多孔材料可以减小储罐内上、下分层之间的压力差,即减小储罐内翻滚事故发生时释放的能量,从而在一定程度上抑制翻滚事故的发生;整体来说,填充厚度越大,压力差越小。
3 结论通过对无多孔材料填充和在边界层填充多孔材料时储罐内液化天然气流动情况进行对比,得出以下结论:
(1) 在储罐边界层填充多孔材料,多孔材料填充部分的流体流速明显比相邻区域小,同时在壁面热边界条件和多孔材料作用下,罐体两边的流动强度较弱,中间的流动强度较强,两侧滚动圈的滞留区面积比中间滚动圈大,且滚动圈的方向是顺时针与逆时针交替出现。
(2) 填充多孔材料可减小流体平均流速,减少压力出口质量流量,减小储罐内上、下分层之间的压力差。
| [1] |
林瑞泰.
多孔介质传热传质引论[M]. 北京: 科学出版社, 1995, 39-47.
LIN R T. Introduction to heat and mass transfer in porous media[M]. Beijing: Science Press, 1995, 39-47. |
| [2] | NIELD D A, BEJAN A. Convection in porous media[M]. New York: Springer, 1999, 23-65. |
| [3] | SHOKOUHMAND H, JAM F, SALIMPOUR M R. The effect of porous insert position on the enhanced heat transfer in partially filled channels[J]. International Communications in Heat and Mass Transfer, 2011, 38(8): 1162-1167. DOI: 10.1016/j.icheatmasstransfer.2011.04.027 |
| [4] | NIMVARI M E, MAEREFAT M, EL-HOSSAINI M K. Numerical Simulation of turbulent flow and heat transfer in a channel partially filled with a porous media[J]. International Journal of Thermal Sciences, 2012, 60: 131-141. DOI: 10.1016/j.ijthermalsci.2012.05.016 |
| [5] |
邢志祥, 杜贞, 张成燕, 等. 密闭储罐内填充非金属多孔材料后预混可燃气体火焰传播的数值模拟[J].
安全与环境学报, 2014, 14(6): 91-95.
XING Z X, DU Z, ZHANG C Y, et al. Simulation for the propagation of the premixed combustible gas flame in a closed tank with non-metal porous materials[J]. Journal of Safety and Environment, 2014, 14(6): 91-95. |
| [6] |
田宏, 王旭, 高永庭. 用于石油液化气体储罐填充的多孔金属材料的防火防爆机理及应用[J].
消防技术与产品信息, 2000(1): 29-30.
TIAN H, WANG XU, GAO Y T. Fireproof and explosion-proof mechanism and application of porous metal materials for filling in petroleum liquefied gas storage tanks[J]. Fire Technique and Products Information, 2000(1): 29-30. |
| [7] |
田宏, 王旭, 高永庭. 多孔填充材料的防火防爆机理及应用[J].
工业安全与防尘, 2000, 26(4): 43-46.
TIAN H, WANG X, GAO Y T. Mechanism of fire protection and explosion suppression of porous materials and application[J]. Industrial Safety and Dust Control, 2000, 26(4): 43-46. |
| [8] |
付全荣. 泡沫金属填充套管换热器内流体流动和传热研究[D]. 太原: 太原理工大学, 2010. FU Q R. Researches on fluid and heat transfer in a double pipe heat exchanger with metal foams[D]. Taiyuan: Taiyuan University of Technology, 2010. |
| [9] |
于明跃. 多孔固体构架与气流对流换热特性数值研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. YU M Y. Numerical study on convection heat transfer of porous materials[D]. Harbin: Harbin Institute of Technology, 2010. |
| [10] |
李泊然. 晃荡条件下LNG液货舱分层与翻滚现象的数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2016. LI B R. Simulation of stratification and rollover phenomenon in the LNG cargo tank under sloshing condition[D]. Harbin: Harbin Institute of Technology, 2016. |
| [11] |
秦允豪.
热学[M]. 2版. 北京: 高等教育出版社, 2004, 154-156.
QIN Y H. Thermal science[M]. 2nd Edition. Beijing: Higher Education Press, 2004, 154-156. |



