2. 中石油物资公司;
3. 西南油气田分公司工程技术研究院;
4. 贵州天然气能源投资股份有限公司
2. China Petroleum Materials Corporation;
3. Engineering and Technology Research Institute of PetroChina Southwest Oil & Gas Field Company;
4. Guizhou Natural Gas Energy Investment Co., Ltd
0 引言
页岩气井体积压裂过程中套管变形问题突出[1-5]。截至2017年7月,威远-长宁页岩气田共压裂水平井141口,其中34口井套管发生变形,共计47处套管变形点,导致桥塞无法坐封到位、压裂段数减少,单井产量明显降低,同时还增加了施工成本和难度,缩短了井的生命周期,影响了压裂整体效果。针对该问题,许多学者开展了相关研究。田中兰和戴强等[6-7]针对井筒温度变化和狗腿角大小等多项因素进行了综合分析,指出外载增加和强度降低是导致套管变形的重要原因;练章华和于浩等[8-9]指出压裂过程中井筒周围岩石强度降低引发了套管挤毁问题;尹虎和W.YAN等[10-12]指出压裂过程中井筒温度变化是引发套管变形的重要影响因素。以上研究或者是针对具体某一个方面展开的,或者是同时讨论多个因素,但是均未考虑岩性界面对套管应力的影响。但是现场统计数据表明61.7%的套管变形点位于岩性界面处[13]。因此开展岩性界面对套管应力影响的研究具有重要意义。
笔者基于页岩气井压裂工程实际,通过力学试验测量了页岩储层各向异性参数,通过建立井筒温度场明确了压裂过程中套管动温度边界条件,在考虑岩性界面的基础上,建立了套管-水泥环-地层有限元模型,计算了非均匀地应力、页岩储层各向异性、瞬态温度-压力耦合作用以及岩性界面对套管应力的影响。研究结果可为页岩气井压裂过程中井筒完整性设计与控制提供参考。
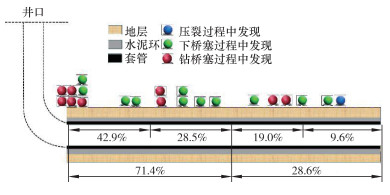
1 威远-长宁页岩气井套管变形特征选择23口井的工程、地质、测井资料进行分析,其中12口水平井出现套管变形,共21处。该23口井水平段最长1 510 m,最短1 045 m,最大分段数24段,最小分段数12段。进行归一化处理后,套管变形点分布位置如图 1所示。套管变形点主要具有以下特点。
|
| 图 1 套管变形点分布 Fig.1 Distribution of casing deformation points |
(1) 从位置分布来看,套管变形点从趾端到跟端不断增多。套管变形点主要集中在水平段靠近跟端的半部分,占已统计套管变形点总数的71.4%,靠近趾端半部分套管变形点数量占28.6%。如果将整个套管水平段分为4部分,可以明显看到从趾端到跟端每一部分套管变形点数量在不断增多。部分套管变形点(占33.3%,7处)位于跟端附近(±100 m)。
(2) 从影响因素上看,11处套管变形点还处于岩性界面处。因此,分析岩性界面对套管应力的影响对于研究页岩气井压裂过程中的套管变形具有重要意义。
(3) 由于水平井筒处于页岩储层当中,必然要受到页岩各向异性的影响,且在压裂过程中整个井筒温度都发生变化,瞬态温度-压力耦合作用也是套管应力分析过程中必须要考虑的因素。
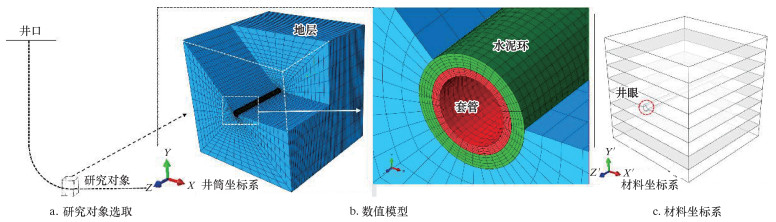
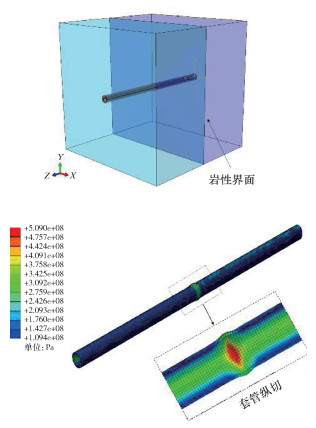
2 数值模型建立考虑套管应力瞬态变化时,受井筒温度变化的影响,水平段同位置不同时刻、同时刻不同位置处套管应力有所不同,选择页岩气井水平段跟端套管-水泥环-地层作为研究对象进行建模,建立套管-水泥环-地层组合体三维有限元模型,如图 2所示。
|
| 图 2 套管-水泥环-地层组合体数值模型 Fig.2 Numerical model of casing-cement sheath-formation |
基于圣维南定理,模型大小为3 m×3 m×3 m,边长为井眼10倍以上。建模过程中,为进一步分析页岩储层各向异性对套管应力的影响,建立材料局部坐标系,坐标轴X′Y′Z′采取与全局坐标系坐标轴XYZ一一对应的方式,O为坐标原点,XOZ与X′OZ′面位于各向同性面内,如图 2c所示。
在载荷施加和边界条件设置方面,采用有限元软件Abaqus中的Predefined功能施加地应力,套管内壁加入液压。温度内边界为动态边界条件,经由井筒温度场模型计算得出,作为随时间变化的动态函数输入到有限元模型中,温度外边界为平行于井筒的模型外壁,为稳定热源。
3 算例及关键参数确定H302-2井为威远-长宁页岩气区块1口实钻井,井深为3 874 m,水平段长1 276 m。地层最大、最小水平主应力分别为84和64 MPa,垂向地应力为52 MPa。地温梯度为每100 m上升3.12 ℃。压裂时施工泵压为82 MPa,排量为16 m3/min,压裂时间为4 h。套管为P110钢级套管,厚度为12.14 mm。其他参数见表 1。
| 名称 | 外径/mm | 弹性模量/GPa | 泊松比 | 热传导系数/
(W·kg-1·℃-1) |
比热容/
(J·kg-1·℃-1) |
密度/
(kg·m-3) |
热膨胀系数/
(10-6 ℃-1) |
| 套管 | 127.0 | 210 | 0.30 | 45.00 | 461 | 7 800 | 13.0 |
| 水泥环 | 168.3 | 10 | 0.17 | 0.98 | 837 | 3 100 | 11.0 |
| 地层 | — | — | 0.23 | 1.59 | 1 256 | 2 600 | 10.5 |
3.1 材料各向异性参数
页岩储层的层理性特征导致其平行层理面和垂直层理面力学效应不同,通常被称为横观各向同性,是各向异性的一种特殊形式,可以用5个独立的弹性常数来表示。基于弹性体中应力应变线弹性关系,本构方程可以表示为:
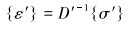
|
(1) |
当XOY为横观各向同性面时:
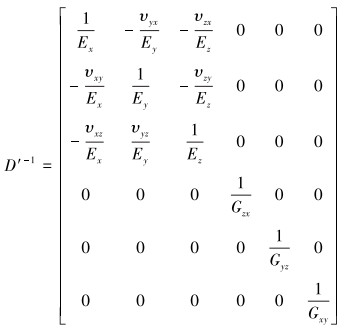
|
(2) |
式中:Ex=Eh为平行于层理面的弹性模量,Ey=Ez=Ev为垂直于层理面的弹性模量,GPa;υxz=υh,υxy=υyz=υv为平行于和垂直于层理面的泊松比。
各向同性面内的剪切模量为:
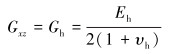
|
(3) |
S.BATUGIN等[14-15]基于大量试验数据,提出了第5个弹性常数的数学解法:

|
(4) |
式中:Gxz=Gh,Gxy=Gyz=Gy,分别为平行于和垂直于各向同性面的剪切模量,GPa。
垂直和平行于层理面的弹性模量和泊松比通过试验得出,Eh=24.91 GPa,υh=0.32,Ev=14.09 GPa,υv=0.36。依据式(1)~式(4)可对其他参数进行求取。
3.2 动温度边界条件参数计算页岩气井压裂过程中,瞬态温度-压力耦合作用始终作用于整个井筒,在计算过程中必须予以考虑,因此建立套管压裂过程中井筒温度计算模型[16],明确数值模型的动温度边界条件。
地层温度与深度呈线性关系:
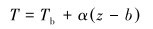
|
(5) |
式中:T表示地层某一点的温度,℃;Tb表示地层恒温点的温度,℃;α表示地温梯度,℃/m;z表示地层某一点的深度,m;b表示基准深度,m。
基于能量守恒原理,对于压裂液单元体,压裂过程中伴随压裂液进出热量的差值、压裂液套内壁摩擦产生热量以及地层传入热量之和等于单位时间内压裂液单元体内热量的变化,即有:
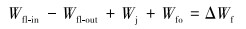
|
(6) |
具体表达式为:
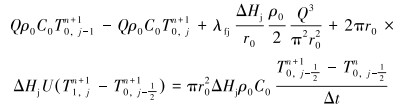
|
(7) |
式中:Wfl-in、Wfl-out分别为压裂液流入带进、流出带走的热量,J;Wj为压裂液与井壁接触摩擦产生的热量,J;Wfo为无限远地层传入的热量,J;ΔWf为压裂液单元体内热量变化,J;Q为压裂液排量,m3/min;ρ为密度,kg/m3;C为比热容,J/(kg·℃);r为半径,m;ΔHj为单元体高度,m; U为流体与套管表面对流换热系数,W/(m2·℃;λfj为套管摩阻系数,与流体雷诺数有关。
对于套管内壁单元,套管壁传入到压力液单元体的热量与地层传入到套管壁上的热量之和,等于套管壁上的热量变化:
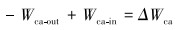
|
(8) |
具体表达式为:
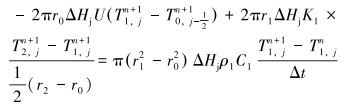
|
(9) |
基于同样的原理,对于套管内壁外的固体单元,套管内壁传入到固体单元的热量与地层传入到固体单元上的热量之和等于固体单元上的热量变化,具体表达式为:
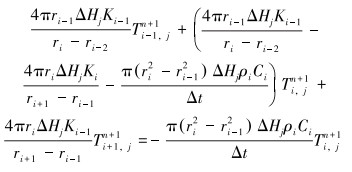
|
(10) |
式中:根据网格划分情况,i=0,1≤i<n,n≤i<m,m≤i<k时,分别代表压裂液、套管、水泥环、地层的相应参数,n、m、k分别代表划分的网格数;Wca-out、Wca-in分别为套管壁传入到压力液单元体的热量与地层传入到套管壁上的热量,J; ΔWca为套管内壁单元体内热量变化,J。
压裂过程中套管壁面对流换热系数与压裂液排量和流态存在一定关系,计算过程中需要予以考虑。结合套管压裂实际对雷诺数进行计算,结果显示套管压裂时井筒内压裂液流态为紊流。换热系数计算公式经过推导可得[3]:
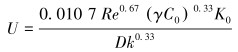
|
(11) |
式中:Re为雷诺数;γ为压裂液表观黏度,Pa·s;C0为压裂液比热容,J/(kg·℃);K0为压裂液导热系数,J/(m·s·K)。
基于前述公式,可以建立页岩气井压裂过程中动温度边界条件表达式:
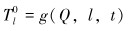
|
(12) |
式中:l代表研究对象到井底的距离,m。
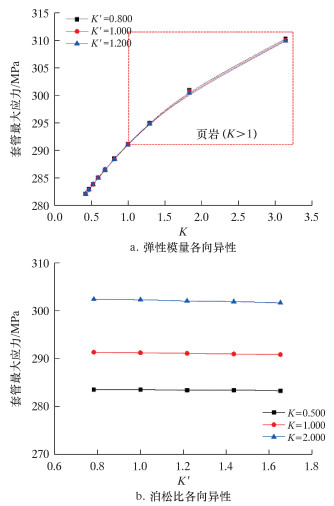
4 模拟结果和讨论 4.1 页岩储层各向异性对套管应力的影响页岩储层各向异性包含弹性模量各向异性和泊松比各向异性。定义页岩层理面弹性模量与法向弹性模量的比值为K,K=Eh/Ev,页岩层理面泊松比与层理面法向泊松比的比值K′,K′=υh/υv,K和K′均为表征材料各向异性的参考值。图 3所示为页岩各向异性对套管应力的影响。
|
| 图 3 页岩各向异性对套管应力影响 Fig.3 Effect of shale anisotropy on casing stress |
由图可知,弹性模量各向异性越强,套管应力越大;泊松比各向异越强,套管应力越小;弹性模量各向异性比泊松比各向异性对套管应力影响更大。试验数据表明:当井下围压达到30 MPa时,K=2.348,K′=1.650,套管应力为305.4 MPa,相对于不考虑各向异性(同条件下各向同性模型计算结果291.2 MPa),提升幅值仅为4.9%,因此页岩储层各向异性不是套管变形的主要因素。
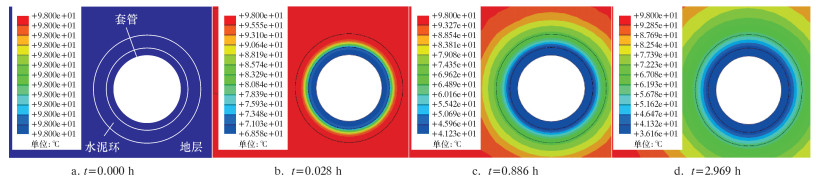
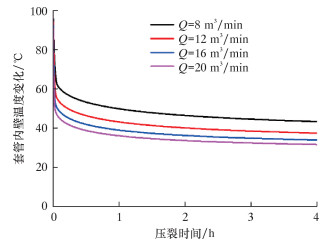
4.2 压裂过程中温度变化对套管应力的影响页岩气井压裂过程中,压裂液与套管直接接触,导致套管在短时间内温度迅速下降,瞬态温度-压力耦合作用明显。基于已建立的井筒温度场模型对压裂液温度进行计算,并且作为动态边界条件输入到有限元模型中。首先得到不同时刻井筒温度分布(见图 4),以及不同排量下套管内壁温度瞬态变化(见图 5)。计算结果表明:压裂过程中套管温度在前0.5 h内下降幅值达到90%以上,并且逐步达到接近稳定的状态。C.SUGDEN等[17]利用商业软件WELLCAT对井筒温度进行了计算,得到了同样的规律,从而也验证了模型的正确性。
|
| 图 4 不同时刻井筒温度分布 Fig.4 Wellbore temperature distributions at different times |
|
| 图 5 不同排量下套管温度瞬态变化 Fig.5 Transient temperature changes of the casing at different displacements |
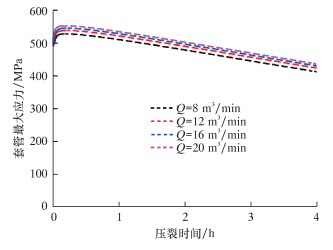
图 6为不同压裂排量下套管最大应力瞬态变化。压裂过程中套管内壁最大应力先迅速升高,然后缓慢下降。主要是因为压裂液进入井筒后,套管内壁遇冷剧烈收缩,外壁则来不及冷却变形,在整体几何条件约束下,变形不协调形成了对内壁收缩的抵制,导致套管内壁受巨大拉应力、外壁受压,因此最大应力迅速增大;压裂一段时间后,套管冷却速度稳定,外壁开始冷却且收缩趋势增强,内部收缩趋势减弱,内拉外压作用减弱,从而使得套管最大应力逐渐减小。排量越大,套管应力最大值也越大。该过程中套管最大应力为545.1 MPa,相比各向同性模型下、仅考虑套管内压和非均匀地应力(291.2 MPa)提升约为87.2%。
|
| 图 6 不同压裂排量下套管最大应力瞬态变化 Fig.6 Transient variation of the maximum stress of casing under different pumping displacements |
4.3 岩性界面对套管应力的影响
地震和测井资料显示,已发生的47处套管变形中61.7%位于岩性界面[13]。基于测井资料数据,利用UMAT子程序将模型材料设置成2部分,第1部分力学性能保持不变,第2部分力学性质设置为E2=38 GPa,υ2=0.36,然后进行计算。计算结果表明:岩性界面交界处套管应力急剧增大(见图 7),相比各向同性模型下、仅考虑套管内压和非均匀地应力(291.2 MPa)提升幅度达到75.6%,为509.0 MPa。
|
| 图 7 岩性界面对套管应力的影响 Fig.7 Effect of lithology interface on casing stress |
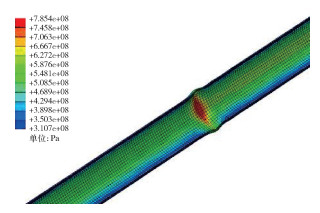
由前述分析可知,页岩气井压裂过程中分析套管应力必须考虑页岩储层各向异性和瞬态温度-压力耦合作用,在套管内压、非均匀地应力以及该2项因素共同作用下,套管应力为574.4 MPa,未达到屈服强度。然后将这些因素与岩性界面共同分析,计算结果表明套管应力为785.4 MPa(见图 8),已经超过P110套管屈服强度(758 MPa)。由此可以说明,页岩气井压裂过程中,套管居中时,岩性界面为套管变形的主要影响因素。
|
| 图 8 多因素耦合作用下套管应力 Fig.8 Case stress under multi-factor coupling |
5 结论
(1) 基于页岩气井套管压裂实际,计算了页岩储层各向异性和温度变化对套管应力的影响。研究结果表明:相比各向同性模型,页岩储层各向异性小幅提升了套管应力;考虑瞬态温度-压力耦合作用时,套管应力先升高、后降低,压裂液排量越大,套管应力越大。
(2) 页岩气井压裂过程中,岩性界面的存在大幅提升了套管应力,是部分页岩气井产生套管变形的主要影响因素。
| [1] |
蒋可, 李黔, 陈远林, 等. 页岩气水平井固井质量对套管损坏的影响[J].
天然气工业, 2015, 35(12): 77-82.
JIANG K, LI Q, CHEN Y L, et al. Influence of cementing quality on casing failures in horizontal shale gas wells[J]. Natural Gas Industry, 2015, 35(12): 77-82. DOI: 10.3787/j.issn.1000-0976.2015.12.012 |
| [2] |
于浩, 练章华, 徐晓玲, 等. 页岩气直井体积压裂过程套管失效的数值模拟[J].
石油机械, 2015, 43(3): 73-77.
YU H, LIAN Z H, XU X L, et al. Numerical simulation for casing failure during volumetric fracturing of shale gas vertical wells[J]. China Petroleum Machinery, 2015, 43(3): 73-77. |
| [3] |
席岩, 李军, 柳贡慧, 等. 瞬态力-热耦合作用下水泥环形态对套管应力的影响[J].
断块油气田, 2017, 24(5): 700-704.
XI Y, LI J, LIU G H, et al. Impact analysis of cement sheath shape on casing stress under transient mechanical-thermal coupling effect[J]. Fault-Block Oil & Gas Field, 2017, 24(5): 700-704. |
| [4] |
席岩, 柳贡慧, 李军, 等. 力-热耦合作用下套管应力瞬态变化研究[J].
石油机械, 2017, 45(6): 8-12.
XI Y, LIU G H, LI J, et al. Study on casing transient stress under thermo-mechanical coupling effect[J]. China Petroleum Machinery, 2017, 45(6): 8-12. |
| [5] |
高利军, 柳占立, 乔磊, 等. 页岩气水力压裂中套损机理及其数值模拟研究[J].
石油机械, 2017, 45(1): 75-80.
GAO L J, LIU Z L, QIAO L, et al. Mechanism analysis and numerical simulation of casing failure in hydraulic fracturing of shale gas formation[J]. China Petroleum Machinery, 2017, 45(1): 75-80. |
| [6] |
田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J].
天然气工业, 2015, 35(9): 70-76.
TIAN Z L, SHI L, QIAO L. Research of and countermeasure for wellbore integrity of shale gas horizontal well[J]. Natural Gas Industry, 2015, 35(9): 70-76. |
| [7] |
戴强. 页岩气井完井改造期间生产套管损坏原因初探[J].
钻采工艺, 2015, 38(3): 22-25.
DAI Q. Analysis of production casing damage reasons during testing and completion of shale gas well[J]. Drilling & Production Technology, 2015, 38(3): 22-25. |
| [8] | LIAN Z H, YU H, LIN T J, et al. A study on casing deformation failure during multi-stage hydraulic fracturing for the stimulated reservoir volume of horizontal shale wells[J]. Journal of Natural Gas Science and Engineering, 2015, 23: 538-546. DOI: 10.1016/j.jngse.2015.02.028 |
| [9] |
于浩, 练章华, 林铁军. 页岩气压裂过程套管失效机理有限元分析[J].
石油机械, 2014, 42(8): 84-88, 93.
YU H, LIAN Z H, LIN T J. Finite element analysis of failure mechanism of casing during shale gas fracturing[J]. China Petroleum Machinery, 2014, 42(8): 84-88, 93. |
| [10] |
尹虎, 张韵洋. 温度作用影响套管抗挤强度的定量评价方法——以页岩气水平井大型压裂施工为例[J].
天然气工业, 2016, 36(4): 73-77.
YIN H, ZHANG Y Y. A quantitative evaluation method for the effect of temperature on casing collapsing strength:A case study of large-scale hydraulic fracturing in shale gas horizontal wells[J]. Natural Gas Industry, 2016, 36(4): 73-77. DOI: 10.3787/j.issn.1000-0976.2016.04.011 |
| [11] |
董文涛, 申瑞臣, 梁奇敏, 等. 体积压裂套管温度应力计算分析[J].
断块油气田, 2016, 23(5): 673-675.
DONG W T, SHEN R C, LIANG Q M, et al. Calculation and analysis of casing thermal stress during stimulated reservoir volume fracturing[J]. Fault-Block Oil & Gas Field, 2016, 23(5): 673-675. |
| [12] | YAN W, ZOU L Z, LI H, et al. Investigation of casing deformation during hydraulic fracturing in high geo-stress shale gas play[J]. Journal of Petroleum Science and Engineering, 2017, 150: 22-29. DOI: 10.1016/j.petrol.2016.11.007 |
| [13] |
陈朝伟, 石林, 项德贵. 长宁-威远页岩气示范区套管变形机理及对策[J].
天然气工业, 2016, 36(11): 70-75.
CHEN Z W, SHI L, XIANG D G. Mechanism of casing deformation in the Changning-Weiyuan national shale gas project demonstration area and countermeasures[J]. Natural Gas Industry, 2016, 36(11): 70-75. DOI: 10.3787/j.issn.1000-0976.2016.11.009 |
| [14] | BATUGIN S A, NIRENBURG R K. Approximate relation between the elastic constants of anisotropic rocks and the anisotropy parameters[J]. Soviet Mining, 1972, 8(1): 5-9. DOI: 10.1007/BF02497798 |
| [15] |
席岩, 李军, 柳贡慧, 等. 页岩储层各向异性对套管应力影响敏感性研究[J].
特种油气藏, 2016, 23(6): 128-132.
XI Y, LI J, LIU G H, et al. Sensitivity study of shale reservoir anisotropy on casing stress[J]. Special Oil and Gas Reservoirs, 2016, 23(6): 128-132. |
| [16] |
席岩, 李军, 柳贡慧, 等. 瞬态力-热耦合作用下水泥环完整性分析[J].
石油钻采工艺, 2017, 39(4): 417-423.
XI Y, LI J, LIU G H, et al. Analysis on cement sheath integrity under transient thermo-mechanical coupling effect[J]. Oil Drilling & Production Technology, 2017, 39(4): 417-423. |
| [17] | SUGDEN C, RING G A, CHAMBERS M R, et al. Special considerations in the design optimization of high rate, multistage fractured shale wells[R]. SPE 151470, 2012. |



