2. 北京工业大学;
3. 西南油气田公司采气工程研究院
2. Beijing University of Technology;
3. Research Institute of Gas Production Engineering, Southwest Oil & Gas Field Company
0 引言
页岩气压裂采用大排量高泵压进行施工,当压裂液注入井筒后,将会对井底温度产生很大影响[1]。赵金洲等[2]通过隐式差分模型计算注液或产液过程中井筒温度场分布。王鸿勋等[3]提出一种非稳态井筒传热新方法,对压裂过程中井筒温度场进行了详细计算。卢德唐等[4]建立多孔介质热传导数学模型,通过数学方法给出了油气井在注入及生产情况下的温度解析解。王六鹏等[5]考虑压裂过程中压裂液的摩擦生热,对井筒温度场进行求解,认为摩擦生热对压裂液温度影响不可忽略。A.SATMAN等[6]针对井筒传热理论进行了深入探讨,理清了静态和瞬态传热的本质,J.Y.YOU等[7]建立一种全隐式算法对井筒及其围岩非稳态温度场进行计算,J.J.CAI等[8]建立耦合模型研究压裂水平井生产过程中温度场分布。
综上所述,虽然国内外学者针对井筒温度场的计算进行了较多的研究,但大部分仅针对油管注入的温度场计算,而对于页岩气井压裂过程中瞬态温度场及温度应力研究较少。鉴于此,笔者基于流变学和热弹性理论,建立压裂过程中套管-水泥环-地层组合体瞬态温-压耦合模型,考虑压裂液流变参数影响,着重分析施工排量、注入温度和施工压力对套管应力的影响,并且根据影响规律提出针对性措施。
1 换热系数 1.1 压裂液流变参数计算压裂过程中所使用的滑溜水压裂液一般为非牛顿幂律流体[9],其流变特性方程为:
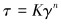
|
(1) |
式中:K为稠度系数,Pa·s-n′;n为流性指数,若n < 1则为假塑性流体,若n>1则为膨胀性流体,对压裂液来说n < 1,即为假塑性流体;γ为剪切速率,s-1。
1.2 压裂液与套管壁间换热系数压裂液泵入井筒后,一般排量很大,因此压裂液处于紊流状态,则压裂液与套管内壁之间换热系数采用Marshall模型进行计算[10],即有:
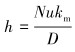
|
(2) |
其中:
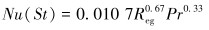
|
(3) |
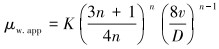
|
(4) |
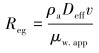
|
(5) |
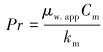
|
(6) |
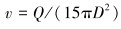
|
(7) |
式中:h为壁面对流换热系数,W/(m2·℃);Nu为努塞尔数;D为计算处的管径,m;Deff为当量直径,m;ρa为钻井液密度,kg/m3;μw, app为表观黏度,Pa·s;v为流体流速,m/s;Q为压裂液排量,m3/min;Cm为比热容,J/(kg·℃)。
由上述方程可计算不同施工排量下压裂液与套管壁之间的对流换热系数,继而可计算井底温度。
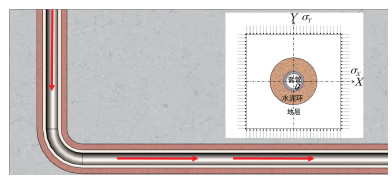
2 模型建立页岩气压裂井在固井水泥浆凝固后,套管、水泥环及井壁围岩将固结为一整体,假设三者接触部位胶结良好、无滑动产生,三者均为均匀各向同性热弹性体[11-12],基于热弹性理论,建立组合体温-压耦合模型,如图 1所示。由于组合体轴向的尺寸远大于径向尺寸,所以将组合体简化为平面应变模型[13],即在径向上有应变,在轴向上没有应变。
|
| 图 1 套管-水泥环-地层组合体温-压耦合模型 Fig.1 Thermal-pressure coupling model of casing-cement sheath-formation |
2.1 热学基本方程
组合体模型基本传热方程如下:
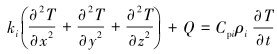
|
(8) |
初始条件为:
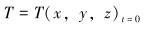
|
(9) |
边界条件如下。
在Γ1边界上:
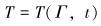
|
(10) |
在Γ2边界上:
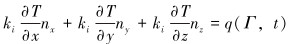
|
(11) |
在Γ3边界上:
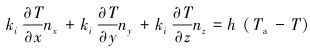
|
(12) |
方程按伽辽金提法的等效积分弱形式为:
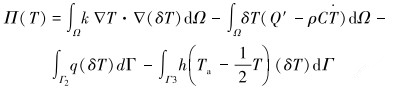
|
(13) |
式中:ki为导热系数(i=1、2、3, 分别表示套管、水泥环和地层导热系数),W/(m·℃);h为流固表面对流换热系数,W/(m2·℃);Cpi为比热容(i=0、1、2、3,分别表示流体、套管、水泥环和地层比热容),J/(kg·℃);ρi为密度(i=1、2、3, 分别表示套管、水泥环和地层),kg/m3;t为时间,s;Ta为套管内壁温度,℃;T为套管-水泥环-地层岩石温度场, ℃;Q′为热源密度,W/m3;q为边界热流密度,W/m2。
将求解域离散为有限个单元,并利用合适的形函数用单元节点的温度值表示单元内温度,可得求取节点温度的有限元求解方程[14]。
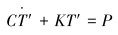
|
(14) |
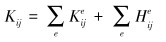
|
(15) |
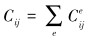
|
(16) |
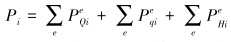
|
(17) |
式中:C为热容矩阵;K′为热传导矩阵;P为温度载荷矩阵;T′为节点温度列阵;Kije为单元热传导矩阵的贡献;Hije为单元热交换边界对热传导矩阵的修正;Cije为单元对热容矩阵的贡献;PQie为单元热源产生的温度载荷;Pqie为单元给定热流边界的温度载荷;PHie为单元的对流换热边界的温度载荷。单元的物理量都可以通过形函数来表示。
2.2 力学基本方程根据弹性理论可得力学基本方程如下。
平衡方程:
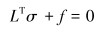
|
(18) |
几何方程:
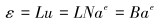
|
(19) |
本构方程:
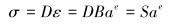
|
(20) |
在Sσ上力边界条件:
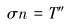
|
(21) |
最小位能的泛函总位能为:
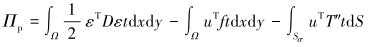
|
(22) |
单元节点与结构节点自由度转换方程为:
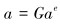
|
(23) |
将求解域离散后,利用各单元总位能可以将系统位能用节点位移a表示,根据变分原理,取泛函一次变分为0,即:
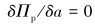
|
(24) |
由此可得泛函的驻值,即为所求的位移向量。可得有限元求解方程:
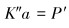
|
(25) |
其中
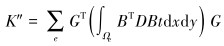
|
(26) |
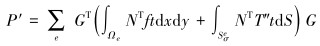
|
(27) |
式中:L为微分算子;σ为应力矩阵;f为体积力;T″为边界面力;u为位移列阵;N为形函数矩阵;ae为单元节点位移列阵;ε为应变列阵;D为弹性矩阵;B为应变矩阵;S为应力矩阵;K″为整体刚度矩阵;a为结构节点位移列阵;P′为结构载荷列阵;G为单元节点和结构节点自由度的转换矩阵;t为厚度。
2.3 温-压耦合方程井筒与地层固结为一个整体,无法自由变形,当温度变化时,就会产生温度应力[15]。温度变化引起的各向同性弹性体温度应变为:
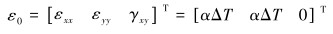
|
(28) |
式中:ΔT为温度变化,℃;α为热膨胀系数,1/℃。
根据最小位能原理可得包含温度应变在内的求解热应力的有限元方程,其形成与式(22)一致,仅载荷向量表达式有所差异:
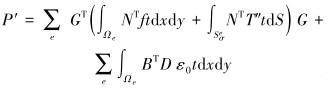
|
(29) |
式(29)与式(27)相比,仅仅多了温度应变引起的载荷项。对于瞬态温度应力计算,由于热学参数在考虑的温度范围内不随时间变化而变化,所以可以选在整个瞬态温度场分析完成后,与力学分析步进行叠加,通过这种方式可以计算在温度和压力耦合作用下组合体的应力变化。
3 参数设置根据弹性力学理论可知,无限大板内圆孔附近会产生应力集中现象[16],但当边界尺寸超过圆孔直径的5倍时应力集中影响就很小,模型基本参数设置如表 1所示。
| 基本参数名称 | 数值 |
| 井眼直径/mm | 215.9 |
| 套管直径/mm | 139.7 |
| 套管壁厚/mm | 9.17 |
| 边界尺寸/mm | 3 000 |
| 套管弹性模量/GPa | 210 |
| 套管泊松比 | 0.3 |
| 套管热膨胀系数/(10-5 K-1) | 1.06 |
| 水泥石弹性模量/GPa | 10 |
| 水泥石泊松比 | 0.17 |
| 水泥石热膨胀系数/(10-5 K-1) | 1.0 |
| 地层弹性模量/GPa | 22 |
| 地层泊松比 | 0.23 |
| 地层热膨胀系数/(10-5 K-1) | 1.02 |
| 最大水平地应力/MPa | 48 |
| 最小水平地应力/MPa | 29 |
| 垂直地应力/MPa | 35 |
| 垂直地应力梯度/(MPa·m-1) | 0.023 |
| 地温梯度/(K·m-1) | 0.025 |
| 泵排量/(m3·min-1) | 1~20 |
| 稠度系数/(Pa·s- n′) | 0.01~1.00 |
| 流性指数 | 0.1~1.0 |
| 压裂液温度/℃ | 100, 150 |
| 比热容/(J·kg-1·K-1) | 3 935, 460, 1 830, 1 043 |
| 热传导系数/(J·m-1·s-1·K-1) | 1.73, 58.20, 1.74, 1.00 |
| 密度/(kg·m-3) | 1 080, 7 850, 1 800, 2 500 |
| 井深/m | 1 500 |
4 结果分析 4.1 换热系数变化
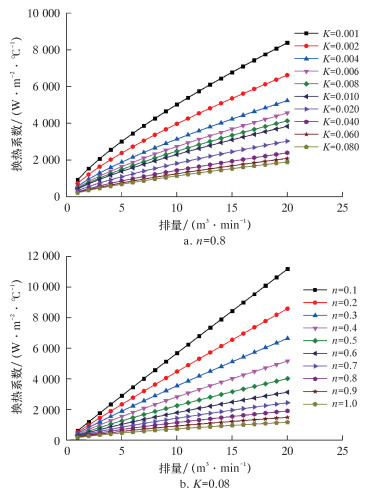
压裂液的流变参数与排量将会影响换热系数[17],由公式(2)~(7)可计算不同流变性参数及排量下换热系数的变化规律,如图 2所示。
|
| 图 2 不同流变参数下换热系数变化曲线 Fig.2 The heat transfer coefficients under different rheological parameters |
由图 2可知,当流变参数n或K不变时,随着泵排量的增加,换热系数随之增大;当排量为定值时,随着流变参数的增加,换热系数先急剧减小,而后缓慢减小。因此,通过改变流变参数和排量可以得到合适的换热系数。
4.2 压裂液瞬态温度场变化取压裂液流变参数K=0.08、n=0.8,压裂排量0、3、6和20 m3/min,计算对应的换热系数,结果如表 2所示。
| 排量/(m3·min-1) | 换热系数/(W·m-2·K-1) |
| 0 | 50 |
| 3 | 107 |
| 6 | 777 |
| 20 | 1 890 |
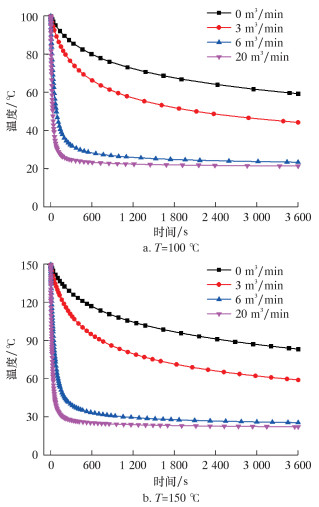
求得换热系数后即可通过式(14),计算储层温度100和150 ℃时井底瞬态温度变化,结果如图 3所示。由图可知,当压裂液排量为0时,井底温度变化较为缓慢,而当压裂液排量增大时,井底温度就会急剧降低。当排量一定时,井底温度越高,温度降低幅度越大,例如100 ℃井底温度时最大温差接近80 ℃,150 ℃井底温度时最大温差接近120 ℃。因此,采用大排量进行压裂施工就会产生较大温差。
|
| 图 3 不同排量下井底瞬态温度变化曲线 Fig.3 The transient temperatures at the bottom of the well with different displacements |
4.3 温-压耦合套管应力变化 4.3.1 施工排量影响
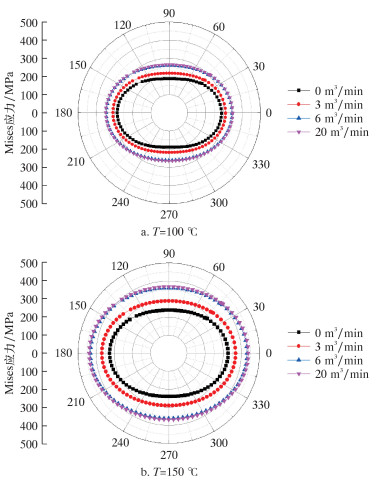
由温-压耦合模型基本方程,将上述计算所得的瞬态温度场变化代入组合体应力模型中,进行温度-压力耦合计算,以此计算不同流量下套管内壁应力变化,结果如图 4所示。
|
| 图 4 不同排量对套管应力影响 Fig.4 Effect of displacement on casing stress |
由图 4可知,随着排量的增加,井底温差增加,套管应力随之增大,而后保持一定数值。同时,地层温度越高,相同排量下井底温差越大,套管应力也会更大。由此可见,在压裂施工中,排量的增加会导致温度剧烈变化,进而增大套管应力。
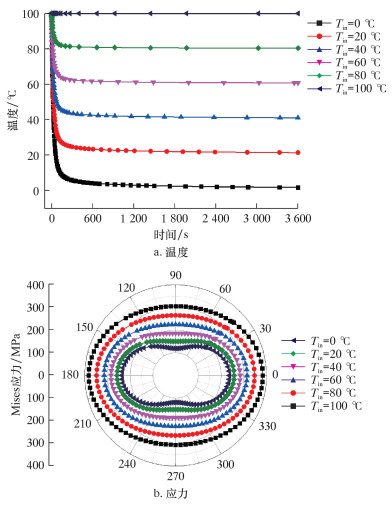
4.3.2 注入温度影响不同压裂液注入温度对套管应力的影响如图 5所示。由图可知,压裂液温度对井底温度和套管应力也会产生较大的影响。随着压裂液温度的降低,井底温度降低幅度增大,套管应力也随之增大。由此可见,在压裂过程中合适的压裂液注入温度有助于降低套管应力。
|
| 图 5 不同压裂液注入温度对井底温度和套管应力的影响 Fig.5 Effect of injection temperatures of fracturing fluids on bottomhole temperature and casing stress |
4.3.3 施工压力影响
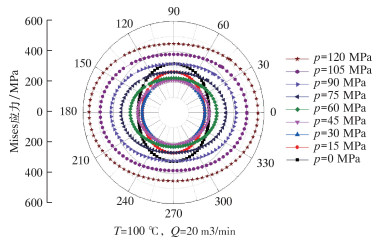
改变施工压力,计算温度-压力耦合条件下套管应力变化,结果如图 6所示。
|
| 图 6 不同施工压力对套管应力的影响 Fig.6 Effect of operating pressure on casing stress |
由图 6可知,施工压力会对套管应力产生一定影响。随着施工压力增加,套管应力先减小后增大,因此适当的压裂压力能够有效减小套管应力。
5 结论(1) 根据页岩气现场压裂施工数据,建立了考虑瞬态温度场变化的套管-水泥环-地层组合体瞬态温-压耦合模型,以此为基础研究了不同施工参数对套管应力的影响。
(2) 通过对压裂液的流变参数进行分析,认为流变参数会影响对流换热系数,继而影响井底温度的变化。因此,应该选择合理的流变参数,改善压裂液与井筒之间的对流换热。
(3) 计算结果表明:压裂液排量增加会迅速降低井底温度,套管应力也随之增加;原始储层温度越高,温度降低的幅度也越大,套管应力增加幅度也大;套管应力随压裂液注入温度降低而增加;合理的施工压力有助于降低套管应力。因此合理的施工泵排量、压裂液注入温度以及施工压力能有效降低压裂过程中井底温度差,从而改善套管受力,保证压裂过程中套管的安全。
| [1] |
董文涛, 申瑞臣, 梁奇敏, 等. 体积压裂套管温度应力计算分析[J].
断块油气田, 2016, 23(5): 673-675.
DONG W T, SHEN R C, LIANG Q M, et al. Calculation and analysis of casing thermal stress during stimulated reservoir volume fracturing[J]. Fault-Block Oil & Gas Field, 2016, 23(5): 673-675. |
| [2] |
赵金洲, 任书泉. 井筒内液体温度分布规律的数值计算[J].
石油钻采工艺, 1986, 8(3): 49-57.
ZHAO J Z, REN S Q. Numerical calculation of liquid temperature distribution in wellbore[J]. Oil Drilling & Production Technology, 1986, 8(3): 49-57. |
| [3] |
王鸿勋, 李平. 水力压裂过程中井筒温度的数值计算方法[J].
石油学报, 1987, 8(2): 91-99.
WANG H X, LI P. Numerical method for calculating wellbore temperature during hydraulic fracturing[J]. Acta Petrolei Sinica, 1987, 8(2): 91-99. DOI: 10.7623/syxb198702012 |
| [4] |
卢德唐, 曾亿山, 郭永存. 多层地层中的井筒及地层温度解析解[J].
水动力学研究与进展, 2002, 17(3): 382-390.
LU D T, ZENG Y S, GUO Y C. Analytical solution of temperature in wellbore and formation in multi-layer[J]. Journal of Hydrodynamics, 2002, 17(3): 382-390. |
| [5] |
王六鹏, 李琪. 垂直井筒压裂温度场分布理论和计算方法研究[J].
科学技术与工程, 2013, 13(35): 10466-10469, 10480.
WANG L P, LI Q. Theory and calculation method study of fracturing temperature distribution in vertical well-bore[J]. Science Technology and Engineering, 2013, 13(35): 10466-10469, 10480. |
| [6] | SATMAN A, TUREYEN O I. Geothermal wellbore heat transmission:Stabilization times for "static" and "transient" wellbore temperature profiles[J]. Geothermics, 2016, 64: 482-489. DOI: 10.1016/j.geothermics.2016.07.003 |
| [7] | YOU J Y, RAHNEMA H, MCMILLAN M D. Numerical modeling of unsteady-state wellbore heat transmission[J]. Journal of Natural Gas Science and Engineering, 2016, 34: 1062-1076. DOI: 10.1016/j.jngse.2016.08.004 |
| [8] | CAI J J, DUAN Y G. Study on temperature distribution along wellbore of fracturing horizontal wells in oil reservoir[J]. Petroleum, 2015, 1(4): 358-365. DOI: 10.1016/j.petlm.2015.10.003 |
| [9] |
李达, 贾建鹏, 滕飞启, 等. 压裂施工过程中的井底压力计算[J].
断块油气田, 2013, 20(3): 384-387.
LI D, JIA J P, TENG F Q, et al. Calculation of bottomhole pressure during fracturing[J]. Fault-Block Oil & Gas Field, 2013, 20(3): 384-387. |
| [10] |
樊洪海.
实用钻井流体力学[M]. 北京: 石油工业出版社, 2014, 399.
FAN H H. Practical drilling fluid mechanics[M]. Beijing: Petroleum Industry Press, 2014, 399. |
| [11] |
殷有泉, 陈朝伟, 李平恩. 套管-水泥环-地层应力分布的理论解[J].
力学学报, 2006, 38(6): 835-842.
YIN Y Q, CHEN Z W, LI P E. Theoretical solutions of stress distribution in casing-cement and stratum system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(6): 835-842. |
| [12] |
李军, 陈勉, 张辉, 等. 水泥环弹性模量对套管外挤载荷的影响分析[J].
石油大学学报(自然科学版), 2005, 29(6): 41-44.
LI J, CHEN M, ZHANG H, et al. Effects of cement sheath elastic modulus on casing external collapse load[J]. Journal of the University of Petroleum, China, 2005, 29(6): 41-44. |
| [13] |
李自平. 大庆油田嫩二底标志层套管剪切失效的有限元分析[J].
断块油气田, 2015, 22(6): 812-815.
LI Z P. Finite element analyses of casing shear failure in Member Ⅱ of Nenjiang Formation in Daqing Oilfield[J]. Fault-Block Oil & Gas Field, 2015, 22(6): 812-815. |
| [14] |
王瑁成.
有限单元法[M]. 北京: 清华大学出版社, 2015, 776.
WANG M C. Finite element method[M]. Beijing: Tsinghua University Press, 2015, 776. |
| [15] | ZHANG L S, YAN X Z, YANG X J, et al. Evaluation of wellbore integrity for HTHP gas wells under solid-temperature coupling using a new analytical model[J]. Journal of Natural Gas Science and Engineering, 2015, 25: 347-358. DOI: 10.1016/j.jngse.2015.05.023 |
| [16] |
李学忠, 刘积松, 董事尔. 高压异常地层局部双层组合套管的设计与应用[J].
断块油气田, 1997, 4(5): 42-46.
LI X Z, LIU J S, DONG S E. Design and application of local double-layer pattern casing of surpressure formation[J]. Fault-Block Oil & Gas Field, 1997, 4(5): 42-46. |
| [17] |
张锋三, 沈一丁, 任婷, 等. 相似雷诺数法在滑溜水压裂管柱摩阻测试中的应用[J].
科学技术与工程, 2016, 16(25): 86-90.
ZHANG F S, SHEN Y D, REN T, et al. Application of similar Renault number standards in string friction test of slick water fracturing[J]. Science Technology and Engineering, 2016, 16(25): 86-90. DOI: 10.3969/j.issn.1671-1815.2016.25.014 |



