2. 中国石油大学(北京)海洋工程研究院
2. Institute for Ocean Engineering, China University of Petroleum(Beijing
0 引言
非黏结柔性立管作为连接海底设施与海上作业平台的枢纽,对于深海油气资源的开采具有重要作用。它主要由金属螺旋缠绕层和聚合物圆柱层复合而成。骨架层作为非黏结柔性立管最内层,由截面近似S形不锈钢螺旋缠绕形成互锁型结构。骨架层的主要作用是承担外部传递来的径向压力[1],因此在工程中对其径向抗压性能研究分析较为成熟。
目前,针对非黏结柔性立管骨架层径向压溃失效研究较多,理论方法主要是根据弹性理论建立圆环挠曲线微分方程,求解径向压力作用下的径向位移[2],并对比分析数值模拟结果,得到骨架层在不同状态下的临界压溃值。在2013年的OMAE会议上,K.A.FARNES等[3]首次提出骨架层新的失效模式,即骨架撕裂,其主要是由骨架层中过大的轴向力引起。目前针对骨架层轴向力学行为的研究较少,笔者对受到轴向变化载荷骨架层的摩擦损失进行研究分析,以期为骨架层端部失效及工程设计制造时的强度计算提供依据。
骨架层截面形状复杂,目前国内外较多学者将其等效为均质螺旋带模型或各向异性圆柱壳进行研究分析[4-5],虽然方法简便,但所有模型与骨架层真实受力情况仍有差别。此时,借助有限元软件对骨架层进行受力分析有很大帮助。任少飞等[6]建立了骨架层三维有限元模型,考虑层间接触,采用质量放大方法解决了计算时间过长的问题,可以有效计算任意载荷及边界条件下立管截面力学性能。T.PEDRIZE等[7]利用ABAQUS软件计算了非黏结性柔性立管在轴向拉力及弯曲载荷作用下的截面力学性能, 通过对比ABAQUS/Standard和ABAQUS/Expilcit 2种算法,采用显式虽然计算时间较长,但可以有效解决计算收敛问题。G.SKEIE等[8]运用ABAQUS和MARC有限元软件对骨架层建模仿真, 计算了不同载荷下骨架层的承载能力,经过试验与有限元模拟结果对比分析,得到骨架层承载能力与内径、骨架层轮廓及钢带厚度等有直接关系。
船舶在海浪的作用下会发生不规则运动,导致连接在下部的柔性立管会受到变化的轴向载荷作用,考虑到骨架层是S形螺旋缠绕的互锁型结构,在外载荷作用下其内部互锁的表面间出现相对运动,从而产生摩擦。在变化的轴向力作用下,骨架层相邻表面接触面面积是个变值,造成骨架层中摩擦力理论计算存在很大的难度。为此,笔者将采用ABAQUS/Explicit算法,考虑相邻表面间光滑摩擦和摩擦因数μ≠0的库伦摩擦2种情况,计算骨架层在变化轴向力作用下的摩擦损失。
1 理论模型根据非黏结柔性立管各层的特点,将骨架层简化为一根螺旋带建立力学模型,求解在轴向力作用下的螺旋带方程。此时包含未知量为螺旋带轴向力F,径向变形量Δr,螺旋角度变形量Δα,轴向变形量Δu,扭转角变形量Δφ。研究中基于以下假设:①轴向伸长率相同;②材料为各向同性线弹性材料;③应变和变形很小;④应力和应变服从均匀分布。
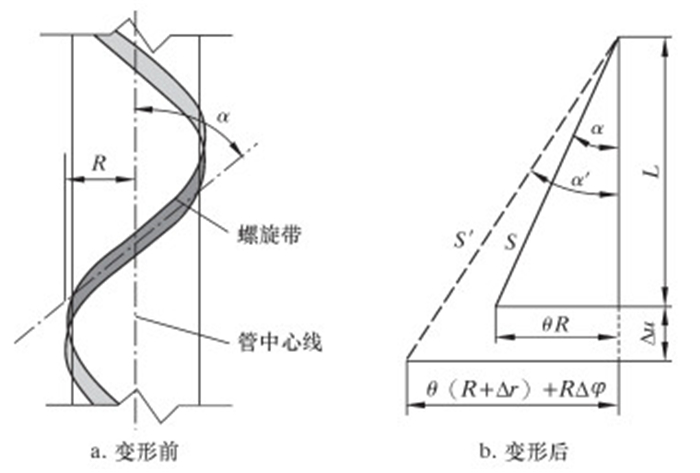
将螺旋带展开成平面直线,在轴对称载荷作用下,螺旋带模型变形前、后形状如图 1所示。图中S和S′分别为拉伸前、后长度,θ为螺旋带缠绕角度,R为骨架层节圆半径,α和α′分别为拉伸前、后螺旋角度,Δr为径向位移[9]。
|
| 图 1 螺旋带变形前、后平面几何形状 Fig.1 The plane geometry of helical strip before and after deformation |
由几何关系可知,螺旋带轴向应变为:
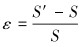
|
(1) |
其中:
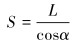
|
(2) |
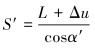
|
(3) |
L和α′可表示为:
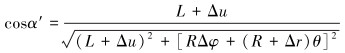
|
(4) |
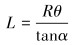
|
(5) |
基于以上假设, 螺旋带轴向应变为[9]:
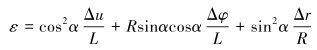
|
(6) |
根据本构关系,轴向力表达式为:
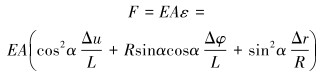
|
(7) |
将螺旋带上轴向力向立管轴向投影,得到轴向力公式:
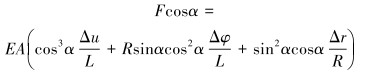
|
(8) |
将螺旋带上轴向力向周向投影,得到螺旋带扭矩公式:

|
(9) |
扭转角度与扭矩关系为:
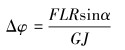
|
(10) |
螺旋角变化值Δα表达式为[10]:

|
(11) |
运用弹性力学知识,径向变化量为:
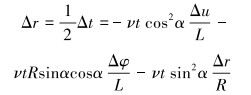
|
(12) |
对于单根螺旋带受轴向力作用时,可联立式(8)~式(12)求解螺旋带各未知变量。
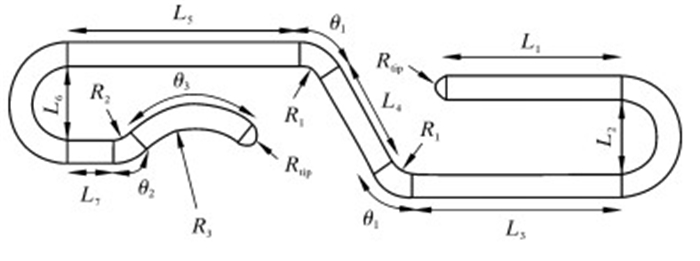
2 有限元计算模型 2.1 几何模型及材料参数由于理论模型做出大量假设,无法考虑骨架层实际模型与相邻表面间的摩擦作用,所以计算结果存在一定误差。骨架层截面如图 2所示。从图中可以看到影响骨架层结构形状的参数有很多,比如钢带厚度、圆弧半径及线段长短等。根据实际结构,笔者将以内径150 mm的骨架层为研究对象。骨架层三维模型具体参数如表 1所示[11-13]。
| 参数 | 取值 |
| E/GPa | 190 |
| L1/mm | 8.0 |
| L2/mm | 3.0 |
| L3/mm | 9.0 |
| L4/mm | 4.5 |
| L5/mm | 10.0 |
| L6/mm | 3.0 |
| L7/mm | 2.0 |
| v | 0.3 |
| θ1/(°) | 60 |
| θ2/(°) | 45 |
| θ3/(°) | 90 |
| R1/mm | 1.0 |
| R2/mm | 1.0 |
| R3/mm | 3.0 |
| Rtip/mm | 0.5 |
|
| 图 2 骨架层截面图 Fig.2 Cross section of the carcass layer |
骨架层材料选用AISI304(奥氏体不锈钢),骨架层结构的缠绕角为87.5°,截面面积A=35.786 mm2,最小转动惯量I=68.108 mm4。
2.2 网格划分与边界条件设置根据实际骨架层建立如图 3所示的完整三维网格模型。运用扫掠映射网格划分模型,其中厚度方向划为2段。采用C3D8单元进行模拟,C3D8是八节点线性六面体单元。线性单元的优势在于受轴向方向载荷时,积分单元不会出现特殊变形,力学行为表现较好,但是在弯扭载荷作用下就会出现剪切自锁等现象,影响模型的计算精度及收敛。因此,在模型受载比较简单而且没有弯曲载荷时,才可考虑使用完全积分单元进行计算。

|
| 图 3 骨架层三维网格模型 Fig.3 3D mesh model of the carcass layer |
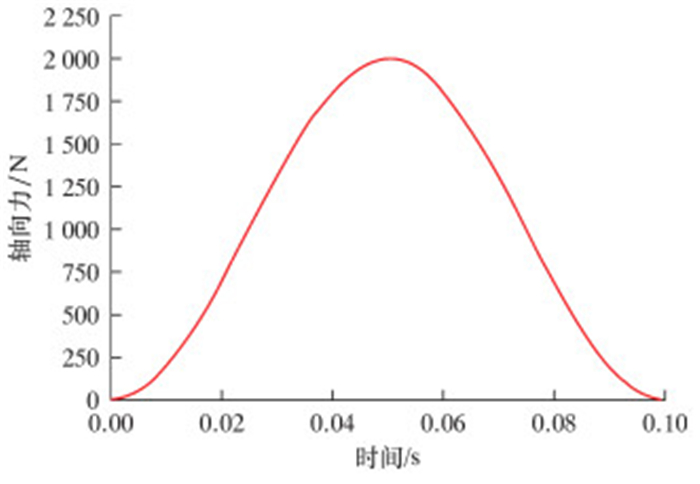
边界条件设置骨架层在X轴正方向端部进行完全约束,限制各个方向位移和旋转。X轴负方向端部限制Y轴方向与Z轴方向位移。为了便于计算截面施加的轴向载荷,将截面上所有点与RP1点进行耦合,如图 4所示。考虑到船舶不规则运动对骨架层的影响,对RP1点施加变化的轴向力F,其大小如图 5所示。

|
| 图 4 骨架层截面耦合设置 Fig.4 Cross-section coupling setting of carcass |
|
| 图 5 变化的轴向力 Fig.5 The variable axial force |
2.3 接触设置
接触问题属于较为复杂的状态非线性问题,接触面之间作用分为切向接触和法向接触。如图 6所示,骨架层在外部载荷作用下,黑色标识的表面容易发生接触。在ABAQUS软件中法向接触行为设置成较为常用的是“硬接触”,即有接触间隙时,接触压力为0。接触距离为0时,接触压力急剧增加为任何可能数值。切向接触行为使用库伦摩擦,其基本概念是将越过接触的最大许用摩擦应力与接触体间的接触应力联系起来。此接触表面为2种情况:①采用通用接触,接触切向设置为光滑摩擦,法向不可穿透;②采用通用接触,接触切向设置为摩擦因数μ≠0的库伦摩擦,法向不可穿透。

|
| 图 6 骨架层相邻接触表面 Fig.6 Adjacent contact surfaces of carcass layer |
3 有限元计算结果 3.1 骨架层应力分析
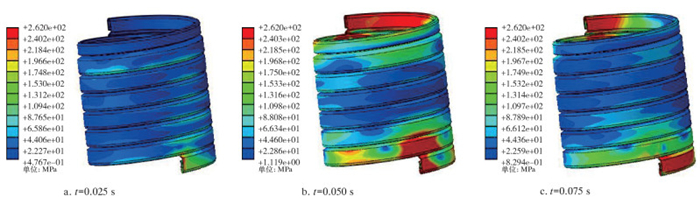
骨架层一端固定,另一端受到变化的轴向力F作用,设置骨架层相邻表面为光滑摩擦,对其进行应力应变分析。由图 5可知,轴向力F变化的趋势是先增大后减小。骨架层不同时刻的Mises应力云图如图 7所示。由图可知,在0.025 s时刻,F=1 000 N,由于载荷沿螺旋骨架层传递作用,初始时刻轴向力作用端面存在较大的Mises应力,上部骨架层应力值较小;在0.050 s时刻,F达到最大值2 000 N,骨架层上、下端面及所延伸区域最大Mise应力达到262 MPa,该部分已发生塑性变形,由于上端面处于完全约束,该区域易发生应力集中;中间部分骨架层应力值明显增大,部分区域达到175 MPa,但仍处在弹性范围内。在0.075s时刻,F=1 000 N,对比图 7b,骨架层上端应力集中区域减少,骨架层中存在残余应力,中间区域骨架层应力值较0.025 s时刻有所增大。
|
| 图 7 骨架层不同时刻的Mises应力云图 Fig.7 Mises stress distribution at different moments in the carcass layer |
3.2 骨架层变形分析
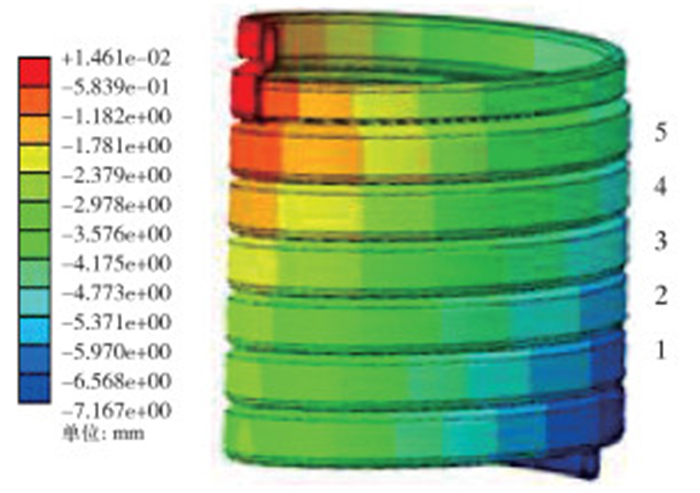
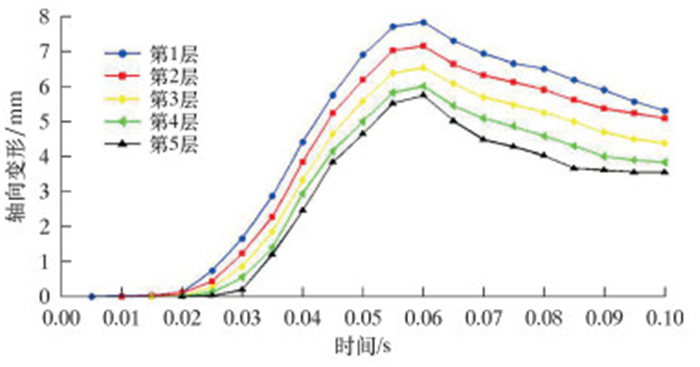
图 8是0.1 s时骨架层的变形情况。由图可知,上端固定约束,轴向位移趋近于0,下端轴向位移7.167 mm;因为骨架层自身属于螺旋缠绕结构,每层变形均是沿着螺旋方向逐渐变化。图 9表示在XY横截面上每层轴向位移随时间变化情况。由于载荷沿螺旋骨架层逐渐传递,各层结构先后被拉伸,在初始状态下各层会在不同时刻出现位移量。大约在0.06 s时,变形位移量最大,在0.10 s时轴向力F大小变为0,各层最终变形量在3.5~6.0 mm之间。从骨架层应力云图中得知,在整个F作用周期内,骨架层上、下端区域已经发生塑性变形,中间部分区域应力值相对较小,材料仍处于弹性范围内,所以在骨架层轴向变形量会出现随着F减小而减小,但最终不会回到原始状态,存在残余变形量。以上分析说明,在实际工程中,骨架层上端部焊接在终端装置内,当柔性立管受到较大轴向载荷,在焊接部位很容易因为应力过大造成骨架层端部变形。K.A.FARNES等在2013年OMAE会议上第1次对骨架层撕裂失效进行了系统性的介绍,他同时也提到,当轴向力过大时,骨架层在焊接点的下部位置容易出现非螺旋状塑性变形。
|
| 图 8 骨架层0.10 s时的轴向变形云图 Fig.8 Axial deformation of carcass layer at 0.10 s |
|
| 图 9 各层节点轴向位移随时间变化关系 Fig.9 The axial displacements of each layer node along time |
4 骨架层摩擦损失计算
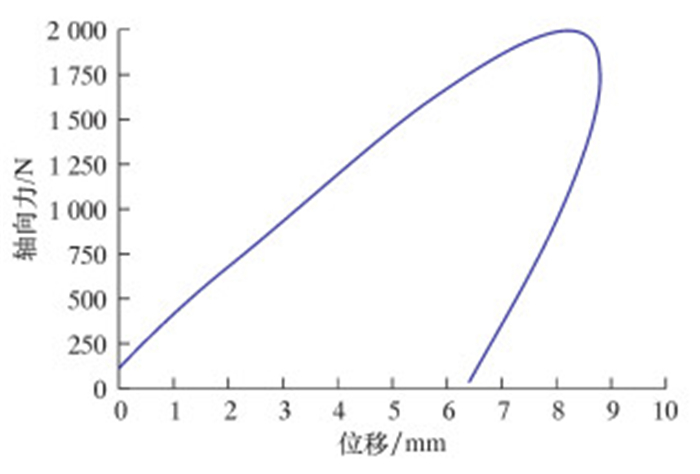
骨架层在轴向力作用下,其特殊的螺旋缠绕结构使相邻表面间更容易发生接触,因为载荷沿各层逐渐传递并且接触面不便于确定,运用理论方法计算骨架层摩擦力做功显得十分困难。在考虑骨架层内部摩擦力时,轴向力F对骨架层做功主要转化为2部分能量,一部分是骨架层产生的变形能,另一部分是克服摩擦力做功所产生的热能。根据能量守恒原理,近似求出骨架层摩擦损失。利用最小二乘法对F作用点位移时间曲线进拟合,将拟合后的作用点位移设置为横坐标,轴向力F设置为纵坐标,绘制F-S图,如图 10所示。图形曲线与坐标轴所包围的面积S代表变化轴向力对骨架层做功WF,它等于骨架层在轴向力作用下产生的变形能Wε与骨架层内部摩擦力做功Wf之和。相应的计算式为:
|
| 图 10 切向摩擦因数μ=0.1条件下节点载荷与位移关系 Fig.10 The node load-displacement diagram under the coefficient of tangential friction μ=0.1 |

|
(13) |
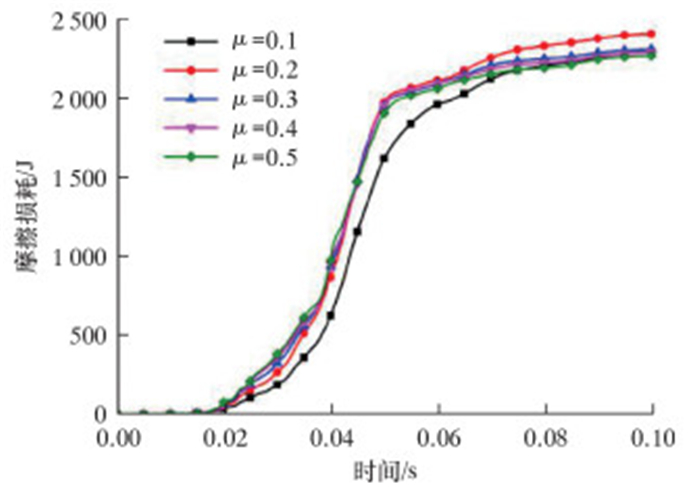
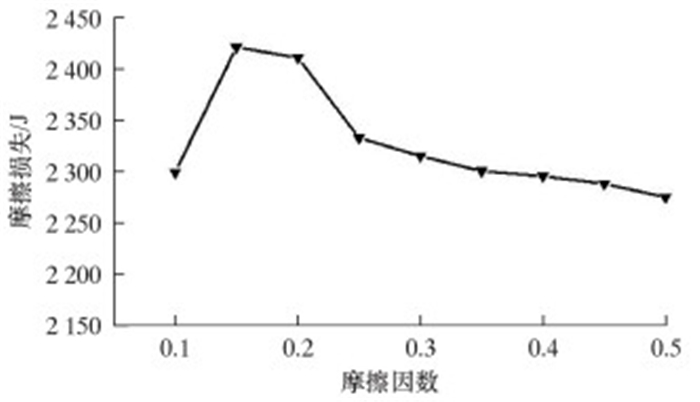
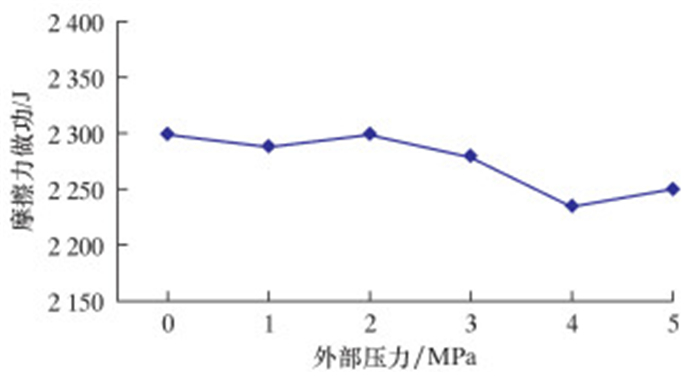
骨架层采用材料为304不锈钢,相邻表面之间在外载荷作用下属于滑动摩擦,在有润滑状态下摩擦因数为0.1~0.3,无润滑状态下摩擦因数为0.3~0.5。图 11表示在不同摩擦因数情况下骨架层内部摩擦力做功情况。在初始状态下,摩擦力做功为0,主要是因为作用在骨架层中轴向力较小,并没使骨架层相邻表面发生接触。在0.02~0.06 s时间内,摩擦力做功迅速增大,骨架层相邻表面间发生严重接触。随着轴向力逐渐减小至0,相邻接触表面逐渐分开,摩擦力不再做功。骨架层摩擦损失随摩擦因数变化曲线如图 12所示。由图可知,摩擦力做功随着摩擦因数的增加先增大后减小,在摩擦因数μ=0.15~0.20时摩擦力做功最大。在摩擦因数逐渐增大时,相邻表面间相对滑动位移会越来越小,导致摩擦力做功也随之减小。对骨架层施加不同的径向外压,结果如图 13所示。由图可知,骨架层没有承载外压时,摩擦力做功2 299 J,当径向外压为1 MPa时,摩擦力做功为2 288 J。随着径向外压逐渐增大至5 MPa,摩擦力做功值也并没有较大变化,这说明在径向外压5 MPa以内时,其外部压力变化对相邻表面间摩擦力做功并没有太大影响。
|
| 图 11 骨架层摩擦损失随时间变化关系 Fig.11 Friction loss of carcass layer along with time |
|
| 图 12 骨架层摩擦损失随摩擦因数变化曲线 Fig.12 Friction loss of carcass layer along with friction factor |
|
| 图 13 骨架层摩擦损失随外压变化曲线 Fig.13 Friction loss of carcass layer along with external pressure |
如果要减小骨架层塑性变形,可考虑在骨架层端部增加摩擦力做功。为了便于表示摩擦力做功在整个系统能量中的作用,可引用文献[14]提出的能量损失因子公式:
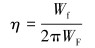
|
(14) |
式中:η表示能量损失因子。
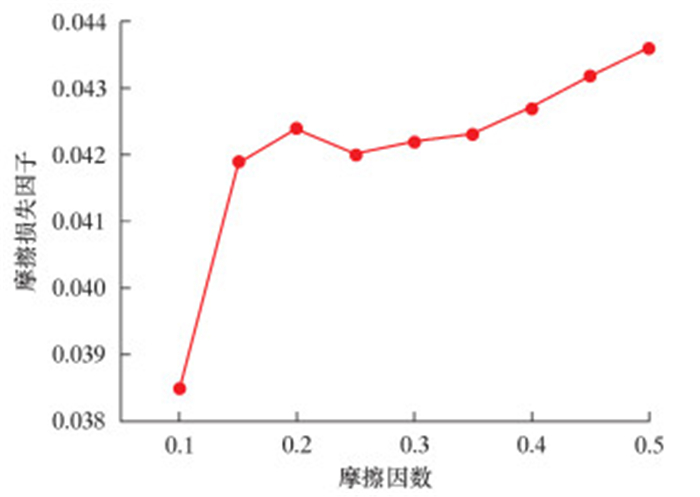
摩擦损失因子随摩擦因数变化曲线如图 14所示。从图中看到,摩擦因数从0.10到0.15时,变化梯度较大,摩擦损失因子从0.038 5增加到0.041 9,在随后的过程中,该因子随摩擦因数逐渐变大。当摩擦因数大于0.25时,摩擦因数变化对摩擦损耗影响较小。
|
| 图 14 摩擦损失因子随摩擦因数变化曲线 Fig.14 Friction loss factor along with friction factor |
5 结论
针对理论方法无法考虑骨架层实际结构和层间接触作用,笔者采用数值模拟方法建立骨架层完整三维模型,运用ABAQUS/Explicit分析了骨架层在轴向变化载荷作用下的应力状态及变形情况,并借助ABAQUS软件分析了不同摩擦因数与不同径向外压下骨架层相邻表面摩擦力做功情况,得到以下结论:
(1) 骨架层在变化的轴向力作用下,上端固定区域与下端施加载荷区域应力较大,这2部分易发生塑性变形,中间部分骨架层应力较小,材料仍处于弹性范围内。最终骨架层被拉伸后仍可收缩,但不可回到初始状态。在实际工程中,应对骨架层固定端进行研究分析,尽量避免塑性变形导致的骨架层失效。
(2) 当摩擦因数在0.15~0.20区间内时,摩擦力做功最大;当摩擦因数大于0.25时,摩擦力做功随着摩擦因数的增加逐渐减小;对骨架层施加径向外压在5 MPa以内时,其外部压力变化对摩擦力做功没有太大影响;摩擦损失因子随着摩擦因数增大而逐渐增大,当摩擦因数大于0.2时,摩擦因数的变化对摩擦损失因子改变影响较小。
| [1] |
王彩山, 汤明刚, 阎军, 等. 海洋柔性管道骨架层径向压缩行为的数值模拟[J].
哈尔滨工程大学学报, 2015, 36(8): 1057-1061.
WANG C S, TANG M G, YAN J, et al. Numerical simulation of the radial compression of carcass layers of unbonded flexible pipes[J]. Journal of Harbin Engineering University, 2015, 36(8): 1057-1061. |
| [2] |
李伟民. 海上建筑非粘结柔性管骨架层径向压溃数值模拟[J].
菏泽学院学报, 2017, 39(2): 65-69.
LI W M. Numerical simulation of radial compression of non-bonded flexible pipe frame in offshore construction[J]. Journal of Heze University, 2017, 39(2): 65-69. |
| [3] | FARNES K A, KRISTENSEN C, KRISTOFFERSEN S, et al. Carcass failures in multilayer PVDF risers[C]//Proceedings of ASME 201332nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes, France: ASME, 2013: V04AT04A024. |
| [4] | PROVASI R, TONI F G, DE ARRUDA MARTINSC. Equivalent model for interlocked carcass under axial loads[C]//Proceedings of ASME 201635th International Conference on Ocean, Offshore and Arctic Engineering. Busan, South Korea: ASME, 2016: V005T04A007. |
| [5] |
董磊磊. 非粘合柔性立管截面特性的理论计算及BSR区域的疲劳分析[D]. 大连: 大连理工大学, 2013. DONG L L. Theoretical prediction of cross-sectional properties and fatigue analysis in the BSR area for unbonded flexible risers[D]. Dalian: Dalian University of Technology, 2013. |
| [6] |
任少飞, 唐文勇, 薛鸿祥. 非黏结柔性立管骨架层失效数值计算方法[J].
上海交通大学学报, 2016, 50(3): 466-471.
REN S F, TANG W Y, XUE H X. Numerical method to predict failure of carcass layer of unbonded flexible risers[J]. Journal of Shanghai Jiaotong University, 2016, 50(3): 466-471. |
| [7] | PERDRIZET T, LEROY J M, BARBIN N, et al. Stresses in armour layers of flexible pipes: Comparison of Abaqus models[C]//Proceedings of 2011 SIMULIA Customer Conference. Barcelona: SIMULIA Customer Conference, 2011: 1-14. |
| [8] | SKEIE G, SKJERVE H, AXELSSON G, et al. Test validation of finite element analysis results of carcass axialcapacity[C]//Proceedings of ASME 201433rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco: ASME, 2014: V06BT04A048. |
| [9] |
郭有松, 陈希恰, 王德禹, 等. 非黏结柔性立管轴对称载荷作用下的结构响应和数值分析[J].
石油学报, 2015, 36(4): 504-510, 515.
GUO Y S, CHEN X Q, WANG D Y, et al. Analytical and numerical investigation on the structural response of flexible risers under axisymmetric load[J]. Acta Petrolei Sinica, 2015, 36(4): 504-510, 515. DOI: 10.7623/syxb201504012 |
| [10] |
陈希恰. 深海柔性立管结构力学特性分析[D]. 上海: 上海交通大学, 2014. CHEN X Q. Analysis of the mechanical property for deep-sea flexible riser[D]. Shanghai: Shanghai Jiao Tong University, 2014. |
| [11] | NOGUEIRA V P P, NETTO T A. A simple alternative method to estimate the collapse pressure of flexible pipes[C]//Proceedings of ASME 201029th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai: ASME, 2010: 693-699. |
| [12] |
汤明刚, 王野, 阎军, 等. 海洋柔性管道骨架层压溃的有限元分析[J].
哈尔滨工程大学学报, 2013, 34(9): 1135-1140.
TANG M G, WANG Y, YAN J, et al. Finite element analysis for collapse of flexible pipes carcass[J]. Journal of Harbin Engineering University, 2013, 34(9): 1135-1140. |
| [13] | TANG M G, LU Q Z, YAN J, et al. Buckling collapse study for the carcass layer of flexible pipes using a strain energy equivalence method[J]. Ocean Engineering, 2016, 111: 209-217. DOI: 10.1016/j.oceaneng.2015.10.057 |
| [14] | UNGAR E E, KERWIN JR E M. Loss factors of viscoelastic systems in terms of energy concepts[J]. Journal of the Acoustical Society of America, 1962, 34(7): 741. |



