0 引言
深水J形管道铺设是一项施工周期长、工艺复杂、受环境影响大的高费用作业,因此在铺管作业之前,应根据拟定的作业环境,对施工中涉及的关键参数进行优化分析,从而通过选择合理的作业参数最大限度地降低发生局部失稳的风险。
管道在下放过程中要承受静水压力、轴力和弯矩的共同作用,极有可能发生局部屈曲,一旦超过了屈曲失效的临界载荷,就会发生屈曲失稳[1]。铺设水深越深,发生失稳的风险越高,其中管道与海床的接触点即着泥点TDP附近是最危险的区域。海底管道处在水下的悬跨段,一方面在轴向力、弯曲和外部静水压力作用下必然产生弯曲变形;另一方面在巨大的复合载荷作用下,局部屈曲几乎不可避免,如果达到了局部屈曲失效的临界载荷,就会发生屈曲失稳,影响正常的铺管作业。
梁振庭[2]和袁林等[3]分别以非线性理论为基础,运用Newton-Raphson迭代法对纯弯曲以及弯曲和静水压组合作用下海底管道的非线性屈曲进行了研究。G.E.HARRISON等[4]采用特征值法对双层管的失稳进行了研究,忽略了海床对外管的影响以及管道初始的几何缺陷,得出了内、外管刚度和夹层厚度对管道整体屈曲的影响。P.JUKES和H.C.RONG等[5-6]系统介绍了双层管研究面临的挑战以及屈曲问题。T.F.ZHAO等[7]运用改进的有限弧长法模拟双层管的侧向屈曲,对顺应式双层管和非顺应式双层管进行了研究,发现对于顺应式结构,短波长和长波长模型都可以模拟其屈曲行为,对于非顺应式结构,内管环向屈曲最有可能导致失效。J.SUN等[8]在考虑管道初始缺陷的基础上,对双层管进行分析,提出了减小内管残余应力,提高高温下承载能力的方法。M.M.HAQ等[9]对影响双层管屈曲参数进行了专门分析,包括管道埋设深度、土壤抗力、土壤特性、外压以及管道的弯曲度,研究结果表明管道的局部屈曲受这些参数和模型边界条件的共同影响。文献[10-12]利用小尺寸模型试验装置对双层管道屈曲进行了试验研究,分析管道位移与临界轴力的关系。韩端峰等[13]综述了S形铺管力学中悬链线法以及奇异摄动法分析对比,介绍了J形铺管在着泥点受力分析的普遍计算方法,讨论了J形铺管管线的形态与受力的解析解情况。
通过上面的文献可以看出,双层管的屈曲问题是一个非常复杂的问题,影响因素较多。目前大多数分析依靠数值计算,还没有可靠的关于屈曲临界应力的解析式。在深水铺设过程中,因局部屈曲引起的失效是最主要的失效模式,随着铺设深度的增加,巨大的静水压力使管道发生局部屈曲失稳的风险进一步加大。鉴于海洋铺管作业高成本的特性,工程上的安全性和工艺上的可靠性是必须优先考虑的因素。因此,如果能建立一个精准的局部屈曲失稳极限载荷的校核模型,在工程设计时,通过数值计算,详细评估发生局部屈曲失稳的风险,将会为J形铺设的安全评估提供理论依据。
1 基于大变形理论的分段模型深水J形铺设中,悬链线模型是描述J形铺设最简单形式。它将管线近似成细缆,忽略弯曲刚度,只承受轴向拉力,假定土壤是刚性,简化为固定平面内的二维模型。
Winkler模型将整个管线分成2部分,TDP左边的位置(已铺设段)考虑刚度作用,以梁弯曲理论建立方程,TDP右边的位置继续使用自然悬链线方程,然后通过TDP的边界条件将2段曲线连接起来,从而得到完整的铺管形态。
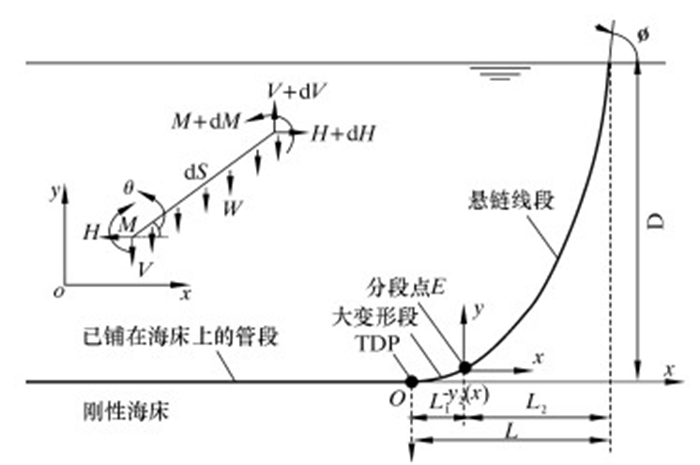
1.1 模型建立笔者采用分段模型对自然悬链线法进行改进。根据J形铺设管道形态(见图 1所示),发现在靠近TDP点(x>0)一段水平距离L1内,管道曲率较大,L2段曲率相对较小,找到管线上曲率小于某值λ的分段点,将整条管线分成2段。将L1段定义为大变形段,应用大变形梁理论进行分析,L2段沿用自然悬链线法的模型进行求解。
|
| 图 1 J形铺管分段模型示意图 Fig.1 Schematic diagram of sectional model of J-lay |
对大变形段L1,利用大变形理论,考虑刚度影响,将微元段看成等截面细直梁,取大变形段任意一点微元dx,则有如下平衡方程:
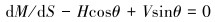
|
(1) |
式中:S为管道长度,θ为管道与水平方向夹角,H、V分别为水平、竖直方向的力,dV/dS=ω,M为弯矩。
根据梁弯曲理论的近似微分方程可得:
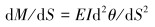
|
(2) |
将式(2)带入式(1)得控制方程:
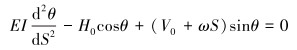
|
(3) |
式中,H0、V0分别为H、V在原点(TDP)的值。
将控制方程无量纲化,令:s=S/L,ω=PL/H0,ε=EI/(H0L2),于是有:
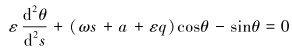
|
(4) |
其中,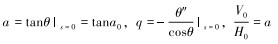
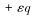
式(4)是典型的二阶非线性微分方程,对于高压大张力的J形铺管而言,由于H0和L数值很大,ε很小,且由于其边界可动,故采用奇异摄动理论求解[14]。奇异摄动理论包括内层展开和外层展开。内层展开适用于边界点附近的求解,如J形铺管中的TDP和顶部分离点附近,外层展开适用于除边界点以外的区域。采用Van Dyke匹配原则[15],在O点和E点邻域使用内层展开,一般区域使用外层展开,假设海床为刚性,将边界条件无量纲:
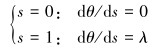
|
(5) |
将函数θ(s,ε)展开成关于ε的幂级数:
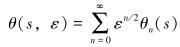
|
(6) |
则q表示为:
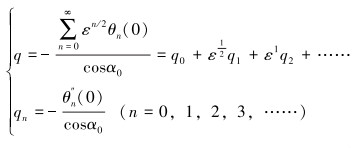
|
(7) |
将式(6)和式(7)带入式(4),并使ε各次幂系数为0,可得到θn(s)的各阶递推方程。
ε0阶:
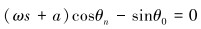
|
(8) |
ε1/2阶:
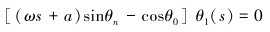
|
(9) |
ε1阶:
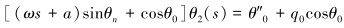
|
(10) |
解方程(8)~方程(10)可得:
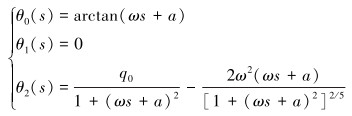
|
(11) |
由式(11)得方程(4)的二阶外场展开解为:
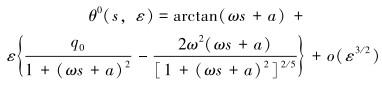
|
(12) |
式(12)的解不满足式(5)的边界条件,对s=0或1的2个边界层区域不适用,只能用在中间部分,因此还需要建立两边界层内的内场近似解。
1.2.2 在TDP附近(s=0端)的内场展开鉴于计算范围很小,引入坐标变换,放大边界层内坐标:引入变量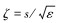
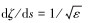
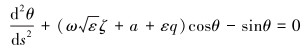
|
(13) |
令θ(s, ε)=φ(ζ, ε)+α0,引入变量β=(1+a2)1/4,则β2=secα0,于是有:
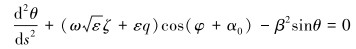
|
(14) |
将θ(s, ε)展成关于ε的幂级数,即:
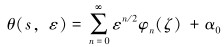
|
(15) |
将式(7)和式(15)带入式(13),展开并使ε各次幂系数为0,得φn(s)的各阶递推方程。
ε0阶:
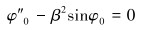
|
(16) |
ε1/2阶:
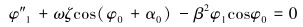
|
(17) |
ε1阶:
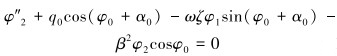
|
(18) |
引入边界条件,根据Van Dyke匹配原则,即n项外场展开式的m项内场展开式等于m项内场展开式的n项外场展开式,可以得出θ在s=0端的二阶内场展开解:
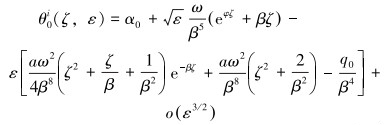
|
(19) |
式中:θi0(ζ, ε)中的i表示内场解,下标0表示s=0处边界层。
1.2.3 在分段点E附近(s=1端)的内场展开与s=0端类似,引入坐标变换,放大边界层内坐标: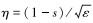
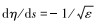
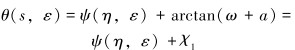
|
(20) |
将式(20)带入控制方程,并引入参数χ=[1+(ω+a)2]1/4,化简得:
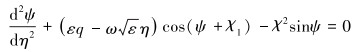
|
(21) |
将ψ(η, ε)展开成关于ε的幂级数,得:
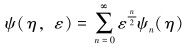
|
(22) |
与前面的求解过程类似,将式(22)带入式(21)展开,使ε各次幂的系数为0,并考虑s=1处的边界条件,再运用Von Dyke匹配原则,得:
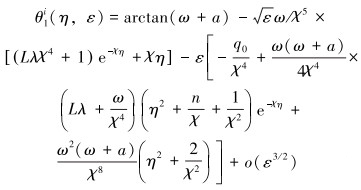
|
(23) |
式(12)、式(19)和式(23)是3个独立的展开解。第1个解θ0(s, ε)适用于除s=0和s=1边界点临近区域外的所有位置,第2个解θ0i(ζ, ε)只能用于s=0临近的小区域内,同样第3个解θ1i(η, ε)只能用于s=1临近的小区域内,在2个边界点附近,它们有重叠的地方,因此应当采用合成的方式,整合得到s∈[0, 1]区间内的一致有效解。可以通过下面公式合成:
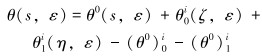
|
(24) |
式(24)中的后2项分别表示s=0和s=1端边界处外场解的内场场限。根据海底水平的假设,有:α0=0, α=tana0=0, χ=[(1+(ω+a)2)]1/4=(1+a2)1/4, β=(1+α2)1/4=1, q0=0,则合成解的表达式为:
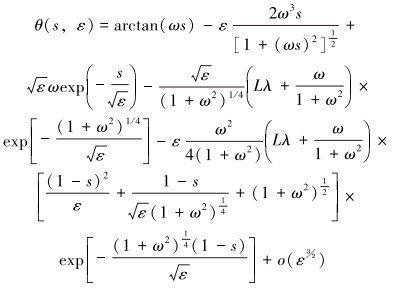
|
(25) |
根据几何关系得:
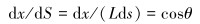
|
(26) |
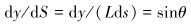
|
(27) |
由式(25)得到管线形态,曲线各点坐标为:
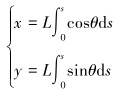
|
(28) |
重新求解后的大变形梁总长可由下式得出:
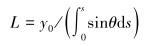
|
(29) |
设分段点E的水平倾角为θe,由θe=θ(1)=arctanω可得:
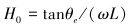
|
(30) |
轴力和弯矩方程如下:
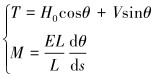
|
(31) |
将轴力、弯矩以及静水压力公式带入DNV-OS-F101[16]校核公式中,可得J形铺管的局部屈曲校核公式,并得出校核系数c。
分段模型的优点:①考虑了EI的影响,模型的计算精度更高;②不需要假设顶端的刚性条件;③自然悬链线法在远离TDP点的计算精度较高、算法简单,大大提高了计算效率。
1.3 计算结果对比分析为了验证分段力学模型的合理性,使用算例进行MATLAB计算分析。选用API规范中的X65钢,海床倾角0°,分段点控制曲率0.004,弹性模量210 GPa,其余参数见表 1。
| 管道外 径/mm |
管道壁 厚/mm |
铺设水 深/m |
铺设角 度/(°) |
海水密度/ (kg·m-3) |
管道密度/ (kg·m-3) |
| 500 | 9.53 | 2 000 | 80 | 1 025 | 7 850 |
1.3.1 管道形态对比分析
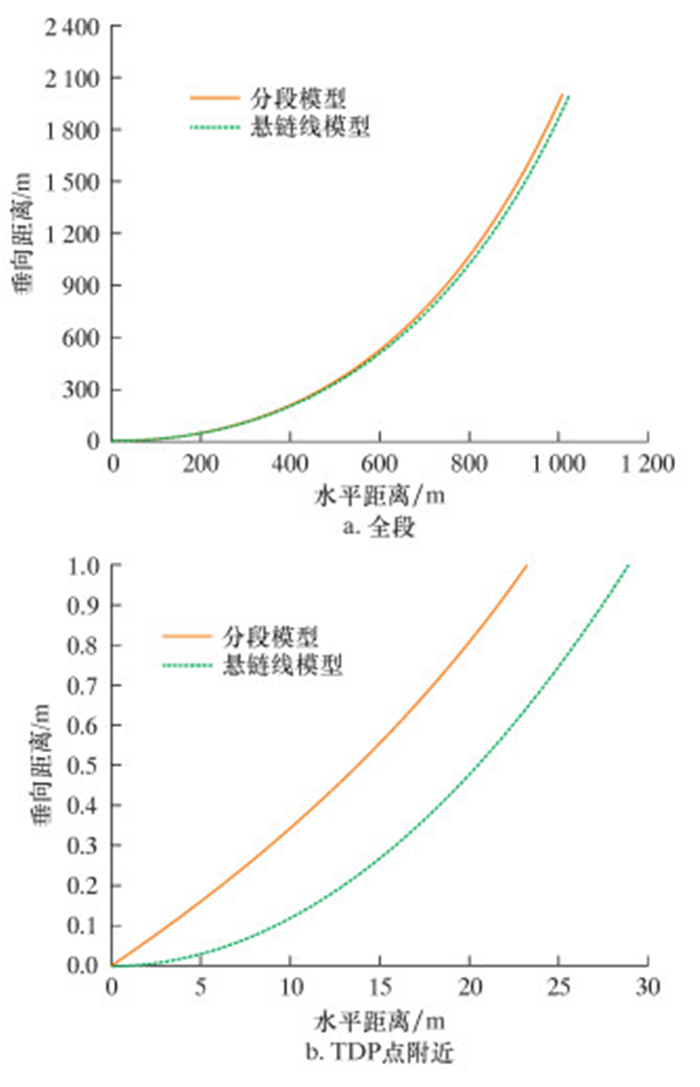
分段模型和悬链线模型对管道形态的计算结果如图 2所示。
|
| 图 2 2种模型形态计算结果 Fig.2 Calculation results of two model configuration |
由图 2a可知,悬链线和分段模型计算的管线形态基本一致。由图 2b可知,分段模型的垂向位移略大,整体上看2种模型的契合度很高。
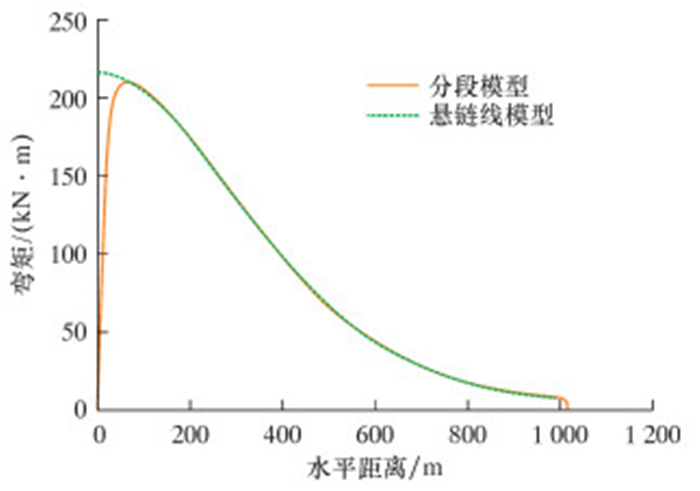
1.3.2 弯矩对比分析用2种模型计算的弯矩如图 3所示。由图可知,自然悬链线模型和分段模型计算的弯矩有很大区别,前者计算的弯矩是间断的,后者计算的弯矩是连续的,出现最大弯矩的位置和大小也不同。对于悬链线模型,x=0时,得Mmax=215.7 kN·m,当x=61.62 m时,得Mmax=209.8 kN·m,两者相差2.9%,除了最大值外,其他部分契合度高,这说明分段模型合理。在J形铺设过程中,弯矩最大位置靠近海床,水深接近铺设最大深度,静水压力大,是容易局部屈曲失稳的部位。因此,克服了悬链线模型局限性的分段模型可以更准确地计算局部屈曲安全评价系数。
|
| 图 3 弯矩计算结果 Fig.3 Calculation results of bending moment |
2 局部屈曲极限载荷参数敏感性分析 2.1 水深变化对局部屈曲的敏感性分析
对于深水J形铺管,水深的变化是局部屈曲控制中最重要的参数,因为水深变化不仅改变了管道的空间形态和内力分布,而且是铺管船上张紧器设计的重要参考。此外,在海底管道铺设过程中,海底的高度差变化也是必须要面对的问题。因此,深入了解影响局部屈曲校核公式中的各种参数随水深的变化规律,有益于预测当水深变化时该如何调整铺管作业中的各个输入参数,并通过监测和止屈技术进行控制,确保铺管作业安全可靠。
首先将DNV-OS-F101极限载荷校核公式[16]进行简化,消去无关的修正系数,得:
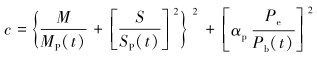
|
(32) |
式中:MP(t)为塑性弯矩抗力,SP(t)为塑性轴力抗力,Pe为管道承受的外压力,αP为流动应力系数,Pb为抗压力系数。
研究发现,管道与海床TDP附近是J形铺管发生局部屈曲失稳的危险区域,即最大弯矩发生位置附近,TDP处管道轴力最小,因此式(32)括号第2项计算值远小于第1项,可以忽略,于是:
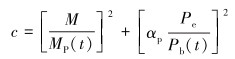
|
(33) |
近一步简化校核公式,令x=0,将式(31)中M带入式(33)得:
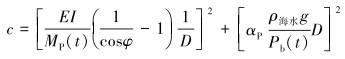
|
(34) |
分析上式可知,EI、MP(t)、αP和Pb(t)只与管道参数有关,cosφ由铺设角度决定。保持表 1中铺管算例分析的各个输入参数不变,将水深设为1 500、2 500和3 000 m,分析水深变化对主要内力以及校核系数的影响,结果如图 4所示。
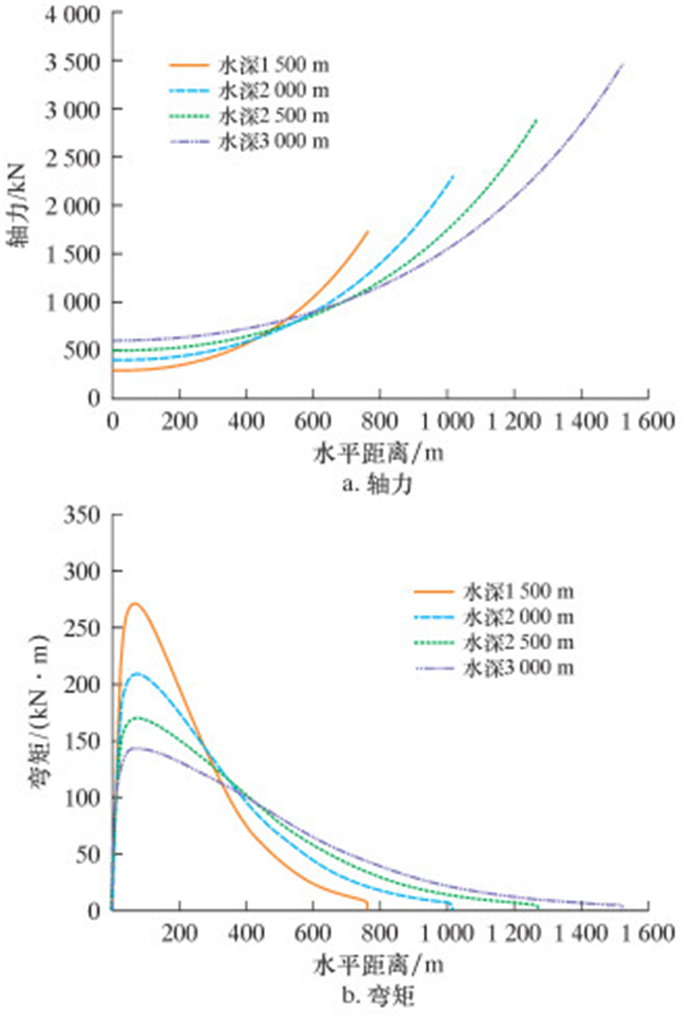
|
| 图 4 水深变化对管道内力影响曲线 Fig.4 Effect of water depth on pipeline internal forces |
从图 4可以看出,随着铺设水深的变化,管道内力分布情况有明显变化。图 4a显示,随着水深的增加,铺管船离TDP点越来越远,J形铺管的悬跨段明显增长,相应的湿重也会增大,张紧器提供的张力增大,管道的轴力也随之增加。因此,对于不同的深度,最大轴向张力不同,水越深,最大轴向力以及TDP附近的轴向张力也增大。图 4b显示,对于给定的水深,弯矩先从TDP点增大,迅速达到最大值,然后逐渐减小,最后趋于0。随着水深的增加,最大弯矩位置离TDP点稍远,但数值变化比较明显,水深越大,管道悬跨段距离增加,曲线变得越来越平坦,弯矩最大值减小。
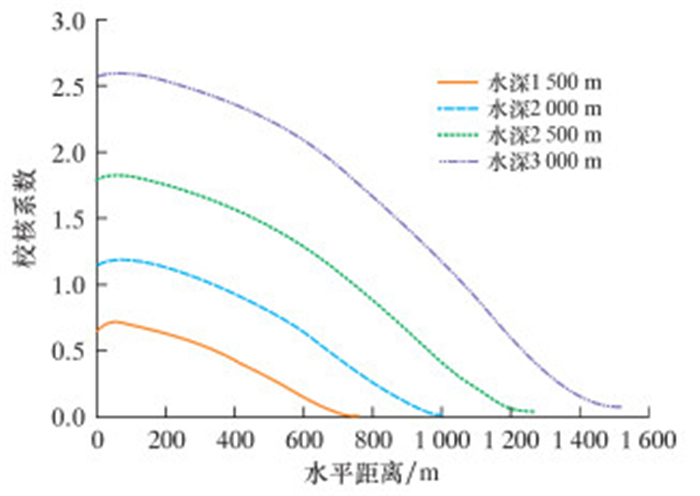
将参数带入公式(34)得到校核系数c的变化曲线,如图 5所示。从图可以看到,校核系数c变化的曲线与弯矩图相似,先增加到最大值,然后逐渐减小,最大值在管道最大弯矩处,这个位置靠近TDP点,因此不同水深下的轴力相差不大,主要影响因素是最大弯矩和静水压力。从1 500 m到3 000 m最大弯矩减小,轴力略微增小,静水压力增加了15.10 MPa,而随着水深增加到3 000 m,静水压力为30.10 MPa,是1 500 m水深的2倍,校核系数显著增大,也说明静水压力是导致管道局部屈曲失稳最主要的外载荷因素。
|
| 图 5 水深变化对校核系数的影响 Fig.5 Effect of water depth on checking coefficient |
综合以上分析,可以得出结论:J形铺管中,在其他参数不变的情况下,随着水深的增加,管道会承受更高的局部屈曲失稳风险,初始缺陷的存在更会降低管道抵抗局部屈曲的能力。
2.2 铺设角度对局部屈曲的敏感性分析J形铺管中,铺管角度的选择与调整是铺管作业的关键,首先通过式(34)分析铺管角度对局部屈曲的影响。分析发现,在其他参数给定的情况下,铺设角度φ越大,cosφ越小,校核系数c越大,因此校核系数c受铺设角度φ的影响,呈正相关关系。然后通过算例分析铺设角度对局部屈曲的敏感性,保持表 1中各个输入参数不变,将铺管角度分别设为75.0°、77.5°和82.5°,分析水深对主要内力以及校核系数的影响,结果如图 6所示。
|
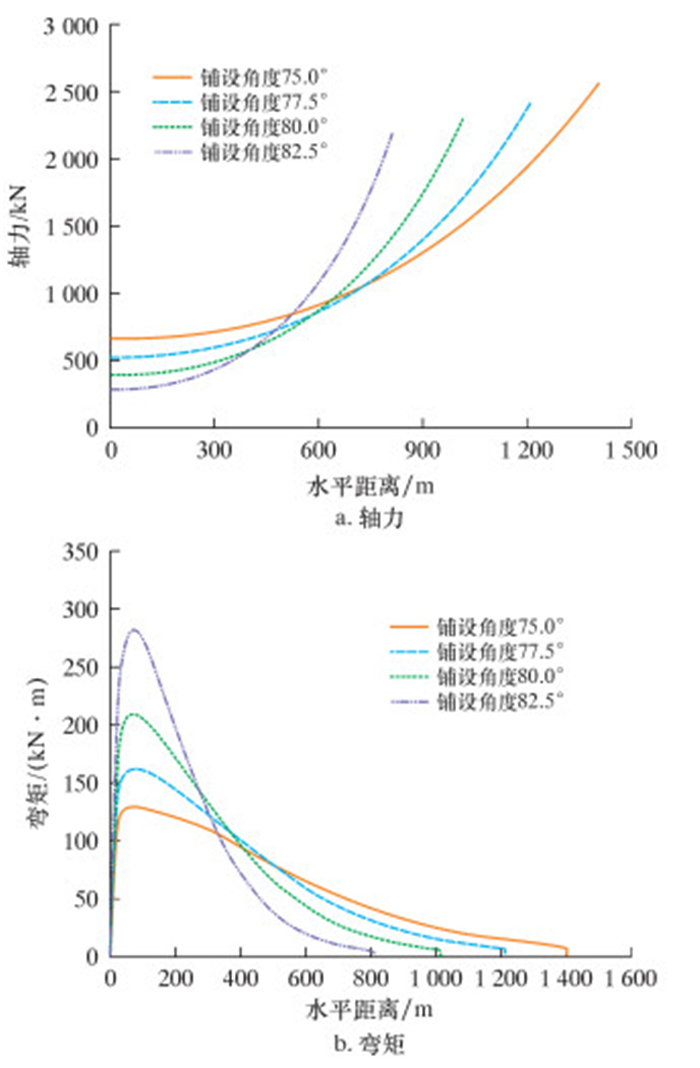
| 图 6 铺设角度对管道内力影响曲线 Fig.6 Effect of laying angle on pipeline internal forces |
从图 6a可以看出,初始倾角不同,管道内力分布也不同;随着铺设角度的增加,管道悬跨段逐渐变得更陡且管线长度减小,从铺管船到TDP的距离减小,铺设角度越大,悬跨段轴向张力越小,TDP附近轴向张力变化随着铺设角度的增加而略微减小。从图 6b可以看出,随着铺设角度的增加,最大弯矩的出现位置略有增加,但最大弯矩明显增加,弯矩曲线形态变得更加尖锐。对于给定的水深,弯矩随着离TDP距离的增加首先增加,迅速达到极值后逐渐减小,直到接近0。
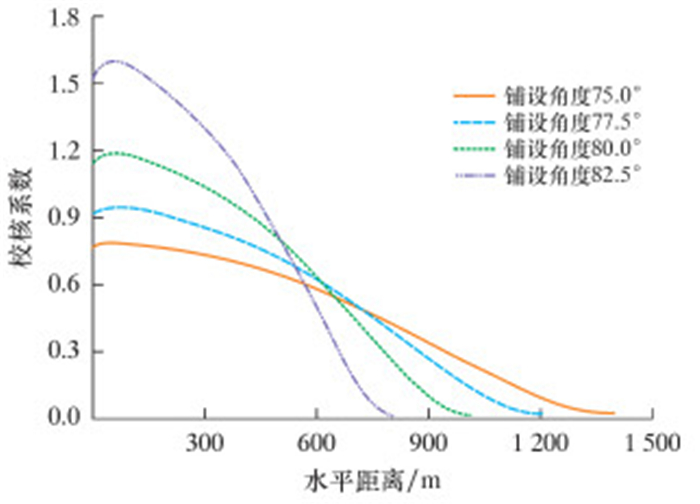
将参数带入公式(34)得到校核系数c随铺设角度变化的曲线,结果如图 7所示。
|
| 图 7 铺设角度对校核系数影响曲线 Fig.7 Effect of laying angle on checking coefficient |
从图 7可知,铺设角度越大,校核系数越大。这是因为弯矩增大时,一旦接近或者大于塑性弯矩抗力MP(t),局部校核系数会急剧变大,但同时管道轴力也会减小,减小校核系数。显然,铺设角度越小,对控制局部屈曲越有利,但是铺设角度受铺管船上张紧器性能的限制,管道下放过程中,必须保证有足够大的张紧力。张紧力有2个作用:一是利用压力产生的摩擦力来平衡管道自身的重力,同时起到固定管道的作用;二是用来保证管线下放过程中的弯曲,即J形铺管形态。
分析可知,铺设角度越小,夹紧相同质量的管道所需要的张紧力越大,而深水铺设管道通常比较长,需要的张紧力非常大,因此铺管角度必须同时满足局部屈曲和张紧力的需求。结合理论分析可以得到以下结论:在深水J形铺设过程中,在局部屈曲不发生失稳的条件下,应选择大角度铺管。
3 结论针对以自然悬链线模型为基础建立的J形铺管局部屈曲失效评价公式的局限性,引入Winkler地基的建模思想对其进行改进,将整个悬跨段分成2段,在接近TDP点附近的大变形段考虑刚度的因素,采用大变形梁理论进行分析,在远离TDP点的悬跨段沿用自然悬链线的算法,得出了更准确的失效评价公式。通过MATLAB对比计算,验证了分段模型的合理性,并且对J型铺管局部屈曲的敏感性参数进行对比分析,得到以下结论。
(1) 分段模型的弯矩连续,弯矩最大位置靠近海床,水深接近铺设最大深度,静水压力大,是容易局部屈曲失稳的部位。与全段应用大变形梁理论求解相比,分段模型迭代求解高阶微分方程的过程更少,减少了计算量,提高了计算速度,可为后续研究提供参照。
(2) 在其他输入参数不变的情况下,单独改变铺设水深和铺设角度,都可以改变校核系数;在其他参数不变的情况下,随着水深的增加,管道会承受更高的局部屈曲失稳风险,管道初始缺陷的存在,更会降低管道抵抗局部屈曲的能力;在局部屈曲不发生失稳的条件下,应选择大角度铺管。
(3) 在静水压力、轴力和弯矩外载荷中,静水压力是对局部屈曲失稳影响最大的因素,J形铺管中,应优先选用大直径的薄壁管,并选取合适的铺管角度以提高管道的抗屈曲能力。只要保证最大弯矩处求解出的校核系数符合规定,就会大大降低铺管过程发生局部屈曲失稳的风险。
| [1] |
陈飞宇, 余建星, 赵羿羽, 等. 复杂载荷条件下有缺陷海底管道非线性屈曲分析[J].
中南大学学报(自然科学版), 2015, 46(7): 2701-2706.
CHEN F Y, YU J X, ZHAO Y Y, et al. Nonlinear buckling of subsea pipes with imperfection under complex loads[J]. Journal of Central South University (Science and Technology), 2015, 46(7): 2701-2706. DOI: 10.11817/j.issn.1672-7207.2015.07.043 |
| [2] |
梁振庭. 深水海底管道铺设受力性能分析[D]. 杭州: 浙江大学, 2008: 8-10. LIANG Z T. Analysis on mechanical performance for deepwater pipe-laying[D]. Hangzhou: Zhejiang University, 2008: 8-10. |
| [3] | YUAN L, GONG S F, JIN W L. Analysis on buckling performance of submarine pipelines during deepwater pipe-laying operation[J]. China Ocean Engineering, 2009, 23(2): 303-316. |
| [4] | HARRISON G E, KERSHENBAUM N Y, CHOI H S. Expansion analysis of subsea pipe-in-pipe flowline[C]//Proceeding of 1997 seventh international offshore and polar engineering conference. Honolulu, USA: ISOPE, 1997: 293-298. |
| [5] | JUKES P, ELTAHER A, SUN J, et al. Extra high-pressure high-temperature (XHPHT) flowlines: design considerations and challenges[C]//Proceedings of the ASME 200928th international conference on ocean, offshore and arctic engineering. Honolulu, USA: ASME, 2009: 469-478. |
| [6] | RONG H C, INGLIS R, BELL G, et al. Evaluation and mitigation of axial walking with a focus on deep water flowlines[R]. OTC 19862, 2009. |
| [7] | ZHAO T F, DUAN M L, PAN X D. Lateral buckling performances of untrenched HT PIP systems[C]//Proceedings of 2007 seventeenth international offshore and polar engineering conference. Lisbon, Portugal: ISOPE, 2007: 945-950. |
| [8] | SUN J, JUKES P. From installation to operation: A full-scale finite element modeling of deep-water pipe-in-pipe system[C]//Proceedings of the ASME 200928th international conference on ocean, offshore and arctic engineering. Honolulu, Hawaii: ASME, 2009: 439-436. |
| [9] | HAQ M M, KENNY S. Assessment of parameters influencing lateral buckling of deep subsea pipe-in-pipe pipeline system using finite element modeling[C]//Proceedings of the ASME 201433rd international conference on ocean, offshore and arctic engineering. San Francisco, California, USA: ASME, 2014: V06AT04A051. |
| [10] |
曾霞光, 段梦兰, 车小玉. 海底埋设双层管管道隆起屈曲分析[J].
海洋工程, 2014, 32(2): 72-78.
ZENG X G, DUAN M L, CHE X Y. Analysis on upheaval buckling of buried subsea PIP pipeline[J]. The Ocean Engineering, 2014, 32(2): 72-78. |
| [11] |
车小玉, 段梦兰, 曾霞光, 等. 双层管道整体屈曲实验研究及数值模拟[J].
应用数学和力学, 2014, 35(2): 188-201.
CHE X Y, DUAN M L, ZENG X G, et al. Experimental study and numerical simulation of global buckling of pipe-in-pipe systems[J]. Applied Mathematics and Mechanics, 2014, 35(2): 188-201. DOI: 10.3879/j.issn.1000-0887.2014.02.007 |
| [12] |
庞熠骞, 段梦兰. 双层海底管道隆起屈曲参数分析[J].
复旦学报(自然科学版), 2015, 54(3): 379-385.
PANG Y Q, DUAN M L. Parametric analysis of upheaval buckling of submarine pipe-in-pipe system[J]. Journal of Fudan University (Natural Science), 2015, 54(3): 379-385. |
| [13] |
韩端峰, 昝英飞, 袁利豪, 等. S型铺管力学计算方法发展现状及技术展望[J].
中国海上油气, 2016, 28(6): 99-107.
HAN D F, ZAN Y F, YUAN L H, et al. Development status and prospect of S-laying mechanical calculation method[J]. China Offshore Oil and Gas, 2016, 28(6): 99-107. |
| [14] | PLUNKETT R. Static bending stresses in catenaries and drill strings[J]. Journal of Engineering for Industry, 1967, 89(1): 31-36. DOI: 10.1115/1.3610004 |
| [15] | DIXON D A, RUTLEDGE D R. Stiffened catenary calculations in pipeline laying problem[J]. Journal of Engineering for Industry, 1968, 90(1): 153-160. DOI: 10.1115/1.3604590 |
| [16] | OCTOBER. Submarine pipeline system: DNV-OS-F101[S]. Oslo: Det Norske Veritas, 2013. |



