2. 中石化胜利石油工程有限公司钻井工艺研究院
2. Drilling Technology Research Institute, Shengli Petroleum Engineering Co., Ltd., SINOPEC
0 引言
随钻扩眼器的工作方式是在钻头钻进的同时对其钻出的井眼进行扩大,该工具目前正在开发和完善,其中扩眼器控制短节的球座周边冲蚀问题凸显出来。目前,可查阅的文献多数是通过Fluent软件对阀座及流道等结构进行流场模拟、数值分析和结构改进,而对随钻扩眼器控制短节中的流体压力控制元件——球和球座的相关研究很少。球与球座之间的密封好坏直接决定扩眼器控制短节的憋压情况,进而决定能否剪掉销钉,心轴能否带动刀翼张开或张开是否到位。因此,需要保证球座的流道结构和材质在投球前有抵抗冲蚀的能力,以保障投球后球与球座良好的密封性能。另外,憋压同时球座下移后,新流道打开,流体仍会冲蚀新流道的相关部位,冲蚀严重会影响控制短节的再次使用。流体流经流道时会与壁面产生摩擦,即冲蚀效果。影响冲蚀的主要因素有流体流速、含砂量和冲蚀时间。用Fluent模拟时无法考虑冲蚀时间,重点考虑流体冲蚀速度,速度越大,冲蚀越快[1]。
笔者主要研究随钻扩眼器未投球时球座入口内壁冲蚀性能及投球后新流道的冲蚀性能[2]。通过Fluent流体模拟软件对流道流场情况进行模拟,以优化流道结构参数,降低冲蚀速度。
1 球座流道有限元分析随钻扩眼器球座位于随钻扩眼器的控制短节内,其流道如图 1所示。投入一枚球,球座卡住球产生憋压,使销钉剪断,球座下移等一系列动作完成后,使扩眼器扩眼短节刀翼张开。

|
| 图 1 流道示意图 Fig.1 Schematic diagram of flow pass 1—球;2—球座外滑套;3—球座;A—流道外扩处;B—流道不变处;C—流道内收处;D—球座上端冲蚀部位;E—外滑套锥面上端;F—外滑套锥面下端。 |
未投球时,流道冲蚀位置在球座内壁和球的密封面上,其流道如图 1a所示。投球后,球及球座等在球座外滑套内轴向下移一定距离,并在球座外罩周边形成了新的流道,如图 1b所示。图中A、B、C表示流道变化情况。
1.1 模型建立应用有限元分析软件ANSYS Workbench建模和划分网格,在Fluent软件中分析2种情况下的流场情况,具体步骤如下。
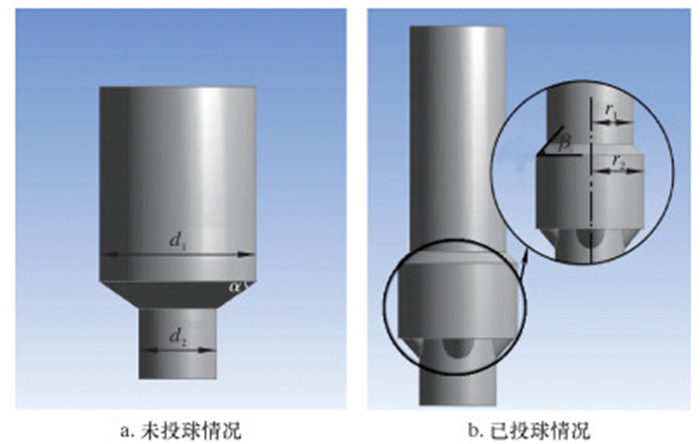
(1) 建立流体模型,如图 2所示。图 2a中,d1为入口直径,α为流道收敛角度,d2为出口直径。原设计球直径55 mm,d1=60 mm,d2=40 mm。图 2b中的原设计参数:r1为入口半径,r1=49 mm;r2是球座上端外部新流道环形空间部分的外径,r2=62 mm。
|
| 图 2 Workbench流体模型 Fig.2 Workbench fluid model |
(2) 采用六面体网格和网格细分命令建立网格模块。
(3) 对模型进行定义。选择标准k-ε两相流模型。
(4) 定义材料。流体定义为钻井液,其密度为1 200 kg/m3,黏度为10-3kg/(m·s)。
(5) 定义边界条件。入口边界定义为质量流动速率入口,入口速率设为28 L/s,入口压力为15 MPa(3 000 m左右的压降),温度313 K,湍流强度5%,水力直径68 mm,水力直径在管内流动中引入,其目的是给非圆管流动取一个合适的特征长度来计算其雷诺数[3-4]。出口设为自由流动出口;迭代步数为5 000步,每10步记录1组数据。
选择相应方法后,通过相应参数的控制条件可以控制收敛条件。模拟的流道流场情况如图 3和图 4所示。

|
| 图 3 未投球时流道冲蚀速度场 Fig.3 Erosion velocity field of flow pass before ball drop |
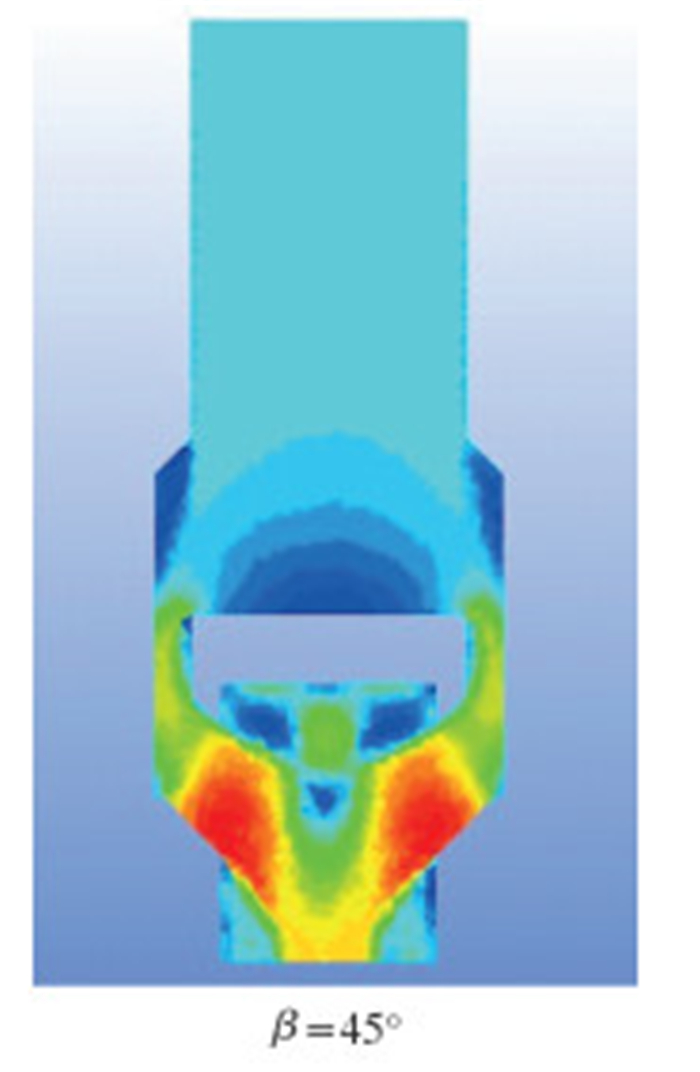
|
| 图 4 投球后流道冲蚀速度场 Fig.4 Erosion velocity field of flow pass after ball drop |
1.2 未投球过程模拟分析
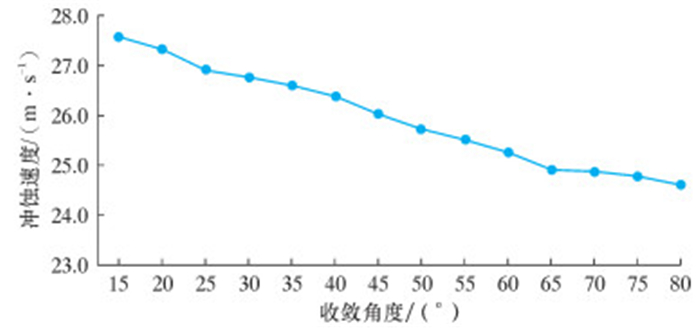
根据以上步骤进行设定,固定入口直径d1=60 mm,出口直径d2=40 mm,只改变图 2a中的α值,得到冲蚀速度随流道收敛角度变化的曲线,结果如图 5所示。
|
| 图 5 入口、出口直径不变,冲蚀速度随收敛角度变化曲线 Fig.5 Effect of convergence angle on the erosion velocity under given inlet and outlet diameters |
随着α的增大,流道变得平缓,冲蚀速度逐渐变小,湍动程度降低,对球座内壁的冲蚀强度变弱。但α值增大而d1、d2不变,会使球座的轴向长度变大,这会引起其他结构尺寸的改变。α值不能无限制的大。另外,α大到一定值时,投球之后球会卡在球座处,卡住球的流道极限角度为81.47°[5]。
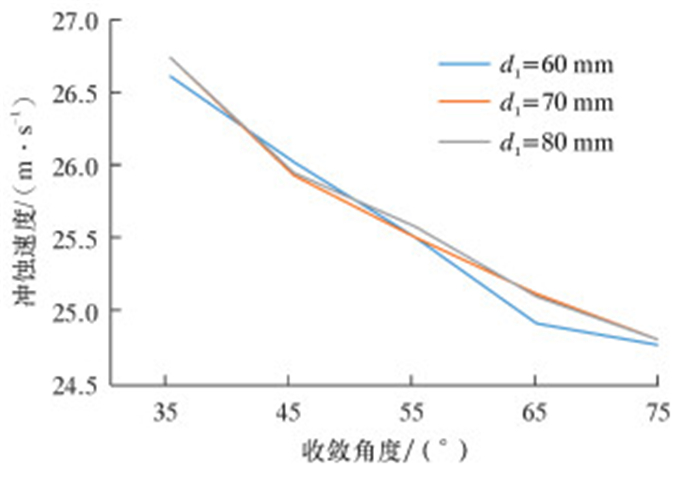
用同样的模拟方法,固定出口直径d2,改变入口直径d1,得到冲蚀速度随收敛角度变化的曲线,结果如图 6所示。从图可以看出,d1分别为60、70和80 mm时3条速度曲线很贴近,这说明在流量值不改变的情况下,增大入口直径对冲蚀速度的影响较小,湍动程度不高。
|
| 图 6 出口直径不变,入口直径变化时冲蚀速度随收敛角度变化曲线 Fig.6 Effect of convergence angle on the erosion velocity under given outlet diameter and different inlet diameters |
根据上述结论,在不改变球座主体尺寸的情况下,优化结果如图 7所示,流道收敛角度α=80°。优化后模拟结果如图 8所示,其最大冲蚀速度为19.69 m/s,是上述算例中最小的,即最优球座结构。

|
| 图 7 优化后的球座关键部位尺寸 Fig.7 The dimensions of key parts of optimized ball seat |
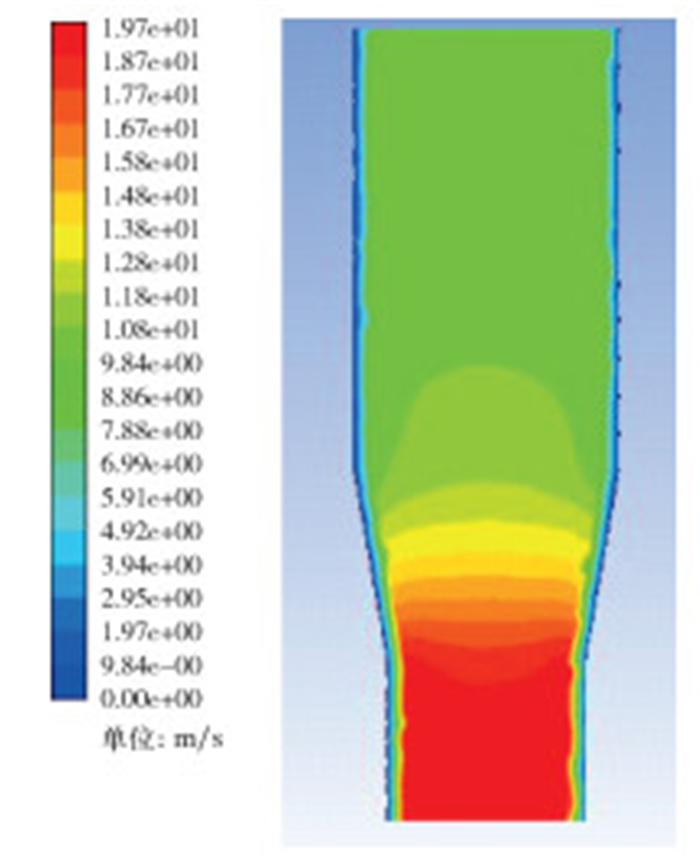
|
| 图 8 优化后的流体冲蚀速度分布云图 Fig.8 The erosion velocity distribution of optimized ball seat |
1.3 已投球过程模拟分析
通过试验可知,投球后A处流道外扩处产生的冲蚀较严重,因此重点对A处流道进行分析和改进。通过变化β来分析流体进入环形空间的速度变化情况,选取较小的冲蚀速度对应的β。模拟计算结果如表 1所示。根据表 1绘制冲蚀速度随β角的变化曲线,结果如图 9所示。
| β/(°) | A处流道冲蚀速度/ (m·s-1) |
全流道冲蚀速度/ (m·s-1) |
| 25 | 7.38 | 13.06 |
| 30 | 6.52 | 12.82 |
| 35 | 5.78 | 11.61 |
| 40 | 5.14 | 10.69 |
| 45 | 5.08 | 10.32 |
| 50 | 5.18 | 10.48 |
| 55 | 5.50 | 10.45 |
| 60 | 5.89 | 10.56 |
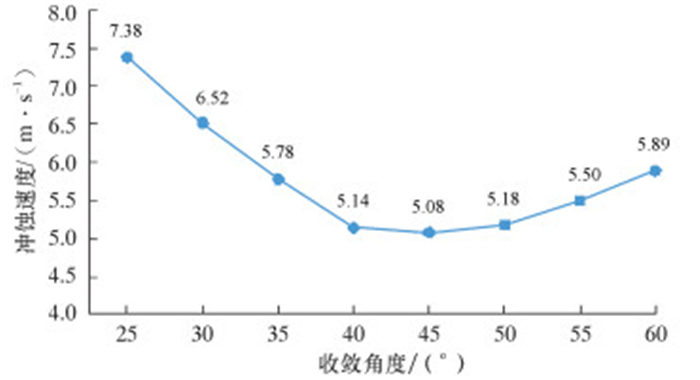
|
| 图 9 改变β角时的冲蚀速度变化情况 Fig.9 Effect of β on erosion velocity |
全流道冲蚀速度是指整个流道流场最大的冲蚀速度。A处冲蚀速度对流道冲蚀影响最大,若严重则会导致再次使用控制短节时,球座上端外部与球座外滑道上端口之间不能有效密封。
由表 1可知,随着β的增大,冲蚀速度减小,对控制短节的冲蚀能力减弱。通过分析可知,β过小会使环形流道变窄,造成憋压;β过大又会导致外扩流道长度增大,从而使图 1b中E点上移或F点下移。E点上移过多会导致投球前球座上端外部与球座外滑道上端口之间密封面在轴向方向变短,影响密封性能;F点下移过多又会使环形流道变窄,导致冲蚀速度加大。β=45°时最好,即r1=49 mm、r2=62 mm、β=45°、h=13 mm为最佳。
2 结论采用Fluent流场模拟软件对扩眼器球座周围流场进行模拟和分析,并优化流道结构,通过分析得到以下结论:
(1) 未投球状态下,冲蚀影响较大位置出现在球座的收缩处,优化后的参数为:流道入口直径d1=60 mm、轴向高度h=46 mm、流道收敛角度α=80°。
(2) 已投球状态下,对冲蚀会影响控制短节再次使用的流道结构进行模拟和优化,结果为:流道入口半径r1=49 mm,球座上端外部新流道环形空间部分的外径r2=62 mm,β=45°,流道轴向高度h=13 mm。
| [1] |
赵阳, 郑政宝. 基于流场仿真的多路阀流道结构优化设计[J].
流体传动与控制, 2007(3): 23-25.
ZHAO Y, ZHENG Z B. Optimum design of flow passage in directional control valve based on flow simulation[J]. Fluid Power Transmission and Control, 2007(3): 23-25. |
| [2] |
王福军.
计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
WANG F J. Computational fluid dynamics analysis:Principles and applications of CFD software[M]. Beijing: Tsinghua University Press, 2004. |
| [3] |
杨源泉.
阀门设计手册[M]. 北京: 机械工业出版社, 2000.
YANG Y Q. Valve design manual[M]. Beijing: China Machine Press, 2000. |
| [4] |
李广军, 王彦枝. 偏心半球阀流场数值模拟与分析[J].
阀门, 2013(2): 33-35.
LI G J, WANG Y Z. Numerical simulation and analysis on flow in eccentric hemisphere valve[J]. Valve, 2013(2): 33-35. |
| [5] |
王朝富, 马浩南, 卢鉴, 等. 强制密封球阀流场模拟分析及优化[J].
油气田地面工程, 2015, 34(11): 87-88, 90.
WANG C F, MA H N, LU J, et al. Simulation analysis and optimization of flow field of forced sealing ball valve[J]. Oil and Gas Field Surface Engineering, 2015, 34(11): 87-88, 90. DOI: 10.3969/j.issn.1006-6896.2015.11.035 |




