2. 中国石油化工股份有限公司上海海洋油气分公司石油工程技术研究院;
3. 中国石油大学(北京)
2. Offshore Petroleum Engineering institute of SINOPEC Shanghai offshore Oil & Gas Company;
3. China University of Petroleum(Beijing
0 引言
目前, 在水平井段以及曲线井段,因为钻具刚度等因素的影响,滑动托压现象频频发生,最终导致定向钻井提速受到限制。顶驱扭摆减阻技术的发展为解决这一问题带来了希望,几年之前,国外斯伦贝谢和CanRig等公司就开始了对该技术的研究工作,并且研制出了新型高效的顶驱扭摆减阻控制系统,该控制系统对于解决滑动钻井过程中的滑动托压问题效果显著[1],在现场应用中极大地提高了机械钻速以及钻井效率[2-3]。到目前为止,国内还没有研制出类似的自动控制系统,在进行定向钻井作业时仍然使用人为控制的方式,根据现场作业人员的经验来输入扭矩极限,扭摆减阻作业效果无法达到最佳,并且容易影响工具面,导致定向钻井的机械钻速和钻井效率都比较低,并且伴有一定的作业风险。
笔者在广泛调研和充分吸收国外相关技术的基础上,拟提供一种适用于扭摆减阻工艺的摩阻扭矩计算模型,并且将模型应用于现场实际钻井作业中,与现场数据进行对比分析,帮助滑动钻进过程中扭摆减阻操作人员及时获取最佳的扭矩极限和扭摆角度,在不影响工具面的情况下,尽量减小钻柱的轴向摩擦阻力,确保扭摆减阻作业能够安全高效地实施,有效解决滑动钻进过程中的滑动托压问题,提高钻井效率。
1 顶驱扭摆减阻工艺原理分析在滑动钻进模式下,可以根据钻井施工中获取的工程数据,利用相关软件分析判断钻柱滑动钻进时的摩阻情况。经过分析计算,利用顶驱(或转盘)旋转控制系统,按照一定的扭矩限定值和扭转角度对钻柱交替施加适当的正扭力和反扭力,使钻柱在周向适当幅度内来回扭摆,从而使得从井口以下到某一井深之间井段中的钻柱运动状态表现为左、右扭摆转动的周向旋转,将该井段中的钻柱与井壁之间的摩擦力由轴向静摩擦力转变为动摩擦力,大大减小钻柱在滑动钻进过程中所受到的轴向摩擦力,消除滑动钻进过程中的托压问题,提高钻井效率,延长水平井水平段长度。
2 建立顶驱扭摆减阻计算模型笔者在充分调研了国内外摩阻扭矩计算模型后[4-6],决定将硬模型与有限元模型相结合,建立一种二维的有限元硬模型。该模型在二维平面空间内对摩擦阻力和扭矩进行分析计算,在计算过程中有以下几个基本假设条件:①井壁为刚性,管柱与井眼轴线的形状基本相同,同时与井壁连续接触;②钻柱的刚性相对较高;③钻柱有扭矩而无弯矩;④动态因素对于钻柱摩阻和扭矩计算结果的影响可以相对忽略;⑤钻柱局部的扶正器、钻柱接头和井径扩大等因素对于模型精确度的影响小,可以忽略;⑥每一个钻柱单元所受的压力、摩擦力和重力均匀分布;⑦忽略方位角对摩阻扭矩计算结果的影响。该模型相对而言,计算简单,对于某些特定井而言,摩阻扭矩计算准确度相对较高,能够为今后在顶驱扭摆减阻技术领域中摩阻扭矩的精确计算起到很好的指导作用。
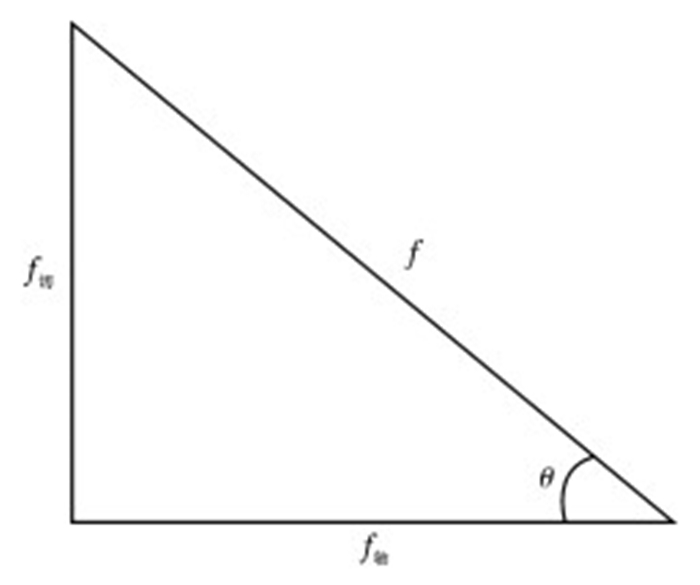
2.1 扭摆减阻钻进摩阻扭矩分析扭摆减阻钻进过程中钻柱与井壁之间的摩阻主要包括轴向摩阻和切向摩阻(动摩擦)2种[7-8]。轴向摩阻是指钻进过程中钻柱沿井壁向下运动,管柱相对井壁发生滑动,因而产生的摩擦阻力。切向摩阻指的是顶驱控制钻柱来回扭摆时,钻柱与井壁接触摩擦产生的摩擦阻力。在钻进过程中,切向摩阻因数跟总摩阻因数并不相等,现场作业时的经验摩阻因数通常是钻柱与井壁之间的总摩阻因数,在钻柱一边旋转一边沿井眼向下滑动的过程中,钻柱会同时受到切向摩阻和轴向摩阻的影响,为了分别计算切向摩阻和轴向摩阻,需要对总摩阻因数进行分解。切向摩阻因数f切、轴向摩阻因数f轴和总摩阻因数f三者之间的关系如图 1所示。
|
| 图 1 摩阻因数关系 Fig.1 Relationship between friction coefficients |
根据图 1所示,轴向摩阻因数、切向摩阻因数和总摩阻因数三者之间存在一定的三角函数关系,因此可以导出如下的关系式:
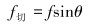
|
(1) |
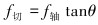
|
(2) |
要计算出切向摩阻因数和轴向摩阻因数,就需要确定θ角的大小。θ角由转速、钻柱外半径和机械钻速三者共同决定,其计算公式如下:
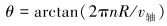
|
(3) |
式中:n为顶驱扭摆转速,r/min;v轴为机械钻速,m/min;R为钻柱外半径,m。
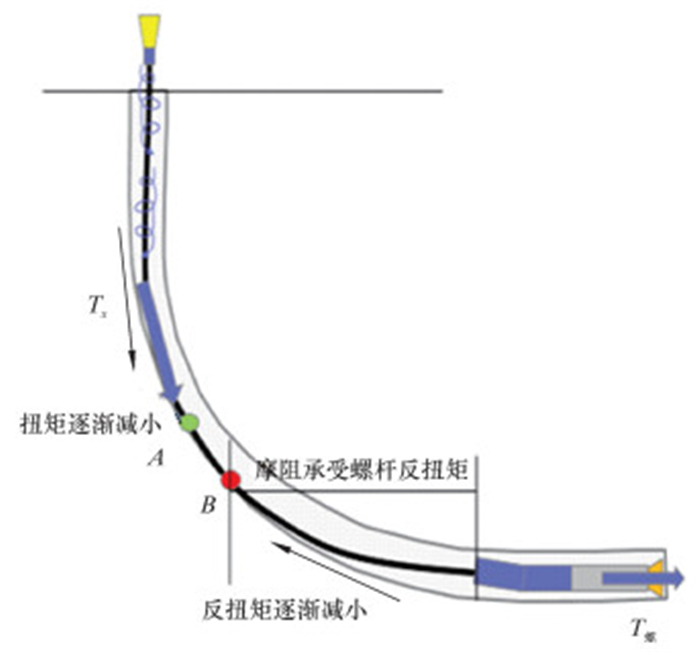
在分析完顶驱扭摆减阻钻进过程中的摩阻后,还要对扭矩进行分析。图 2所示为扭摆减阻钻进扭矩分析,对顶驱扭摆减阻钻进过程中的扭矩分析可通过图片形式更直观地呈现出来。
|
| 图 2 扭摆减阻钻进扭矩分析 Fig.2 Torque analysis on torsion and oscillation drag-reduction drilling |
如图 2所示,在理想工具面时,通过顶驱左、右旋转钻具,顶驱扭矩Tx将会沿着钻具向下传递,同时钻具旋转摩擦会产生一个摩擦反扭矩,该反扭矩与顶驱扭矩方向相反,能够抵消顶驱扭矩。当扭矩传递到井下钻具某一点时,摩擦反扭矩恰好能够克服顶驱扭矩,在该点处钻具就会停止旋转,该点在图 2中标记为A点;同时,在井底由于螺杆钻具旋转会产生一个反扭矩T螺,反扭矩向上传送至钻具的某一位置,即图 2所示的B点,在B点处钻具停止旋转。B点就是钻具克服井底螺杆钻具反扭矩的位置,称B点为干扰点,B点与钻头之间的区域称为干扰区。随着顶驱左、右旋转圈数的增加,顶驱扭矩不断增大,A点会不断下移,当A点移动到B点以下时,即A点进入到干扰区时,将会影响到工具面角。为了避免A点进入干扰区域,需要依据每次现场作业过程中所采集到的钻头悬空扭矩和钻进扭矩,设置一定的安全余量,通过精确计算控制钻具左、右旋转。
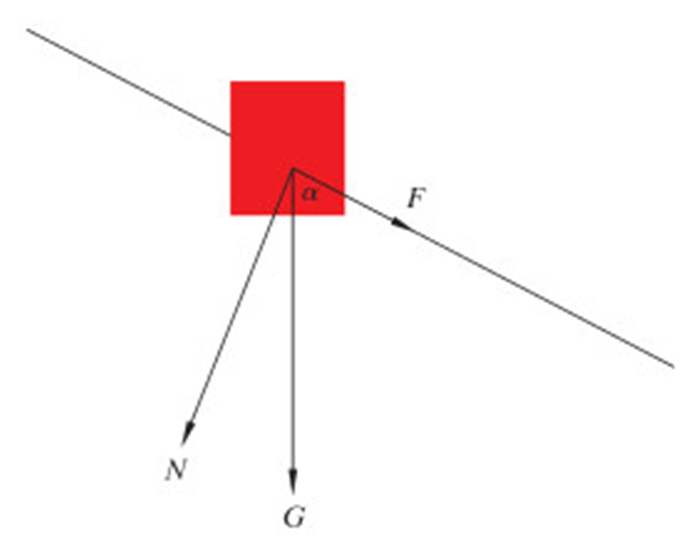
2.2 建立释放摩阻和钻柱扭矩的计算模型建立释放摩阻和钻柱扭矩计算模型,需要对钻柱的受力情况进行分析,利用微积分思想,取钻柱单元体对其进行受力分析。钻柱单元体受力分析如图 3所示。
|
| 图 3 钻柱单元体受力分析 Fig.3 Force analysis of the drill string unit |
钻柱单元体在钻井液中的浮重和钻柱单元体与井壁正接触应力的计算公式如下:
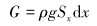
|
(4) |
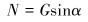
|
(5) |
式中:G为钻柱单元体在钻井液中的浮重, N;N为钻柱单元体与井壁正接触应力, N。
知道了钻柱与井壁正接触应力、钻柱半径以及钻柱与井壁的周向摩擦因数后,就能够求解钻柱扭矩了。钻柱受到的摩擦扭矩如图 4所示。
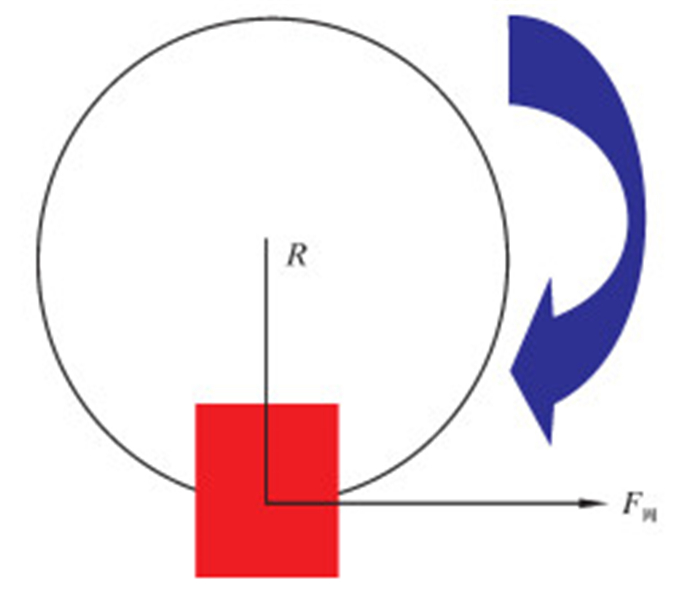
|
| 图 4 扭矩示意图 Fig.4 Torque diagram |
钻柱所受的摩擦扭矩计算式为:
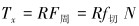
|
(6) |
式中:R为钻柱外半径,m;F周为钻柱受到的周向摩擦力,N。
因此,根据以上分析,可以得到钻柱扭矩和释放摩阻的计算公式。
钻柱扭矩为:
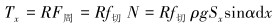
|
(7) |
释放摩阻为:
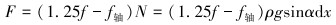
|
(8) |
式中:α为井斜角度,(°);Sx为井深x处钻柱横截面面积,m2;x为井深,m;ρ为钻柱在钻井液中的相对密度,kg/m3。
钻柱在钻井液中的相对密度等于钻柱密度减去钻井液密度。资料显示,通常情况下静摩擦因数是动摩擦因数的1.25倍。顶驱扭摆减阻技术原理是变静摩擦为动摩擦,而释放摩阻的含义正是静摩阻与动摩阻之差,因此计算释放摩阻时需要在动摩阻因数f前乘上1.25。
将钻柱扭矩、释放摩阻和释放钻压沿钻柱从地面往下积分到深度x处可得到如下计算模型。
钻柱扭矩:
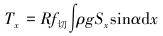
|
(9) |
释放摩阻:
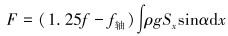
|
(10) |
为了计算方便,将钻柱模型离散化,采用有限单元法,以每1 m钻柱为1个计算单元,从地面往下用迭代累加的方法计算,取n=1, 2, 3,……。则钻柱扭矩计算模型为:
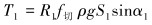
|
(11) |
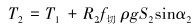
|
(12) |
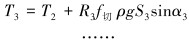
|
(13) |
释放摩阻计算模型为:
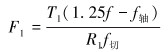
|
(15) |
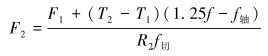
|
(16) |
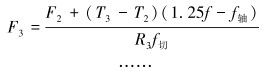
|
(17) |
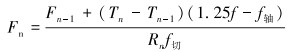
|
(18) |
扭转角度为:
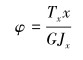
|
(19) |
其中
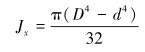
|
(20) |
式中:Jx为井深x处钻柱的极惯性矩;G为井深x处钻柱的切变模量,钻杆、钻铤和方钻杆的切变模量差距很小,通常取80 GPa;D为钻柱外径,m;d为钻柱内径,m。
2.4 扭矩控制范围初步确定扭矩的控制原则为既能释放足够的轴向摩阻,使得在滑动钻井中能给钻头提供作业所需的钻压,又不能改变滑动钻进中工具面方向。具体控制范围如下。
最大控制扭矩:
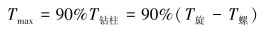
|
(21) |
式中:T旋是全旋转钻进(钻柱旋转加螺杆旋转)的扭矩。
最小的控制扭矩:
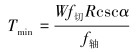
|
(22) |
式中:W是施加的钻压。
释放足够的轴向摩阻,从而为钻头提供作业所需的钻压,这需要用到最小控制扭矩作为控制变量。为了不改变滑动钻进中工具面方向,需要以最大控制扭矩作为控制变量。
2.5 闭环扭摆减阻工艺实施流程(1) 了解当地钻井中的经验摩阻因数(或利用现场数据计算),收集试验井的轨迹数据、井眼数据和管柱数据等。
(2) 根据厂家提供的螺杆钻具工作特性,建立螺杆钻具输出扭矩和压差之间的关系模型。
(3) 将试验井数据(轨迹数据、井眼数据和管柱数据等)录入到摩阻扭矩计算软件中,将计算系统与录井仪连接,实时获取相关钻井参数(钻井液密度、钻速和扭摆转速等),并且将钻井参数也导入到计算软件中。
(4) 先将顶驱扭摆减阻控制系统与顶驱控制台对接,再将摩阻扭矩计算软件输出的钻柱扭矩极限和顶驱扭转角度等数据实时传递给顶驱控制系统。
(5) 顶驱自动按照控制程序进行扭摆减阻作业,控制扭矩随井深动态调整。
(6) 施工中以最大扭矩作为主要控制参数,相应的钻柱旋转角度作为扭矩控制的辅助控制参数。
(7) 扭摆减阻中注意根据需要适当调整顶驱载荷(上提吊打或下压)。
3 顶驱扭摆减阻模型实际应用笔者根据建立的顶驱扭摆减阻模型编制出一套基于顶驱扭摆减阻的摩阻扭矩计算软件,并且将软件应用于现场作业。软件界面如图 5所示。
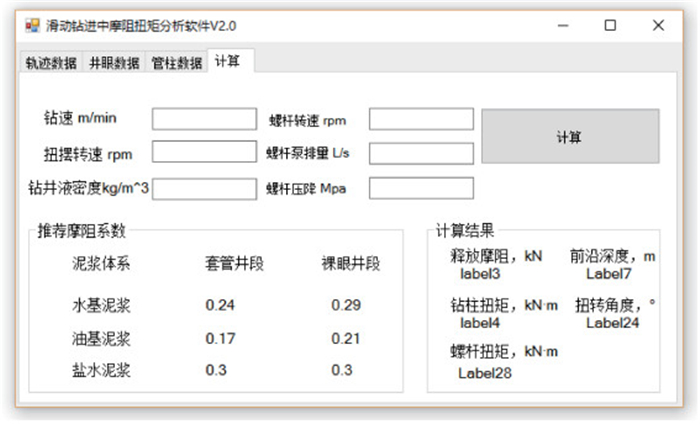
|
| 图 5 软件界面 Fig.5 Software interface |
选取L26-1井和D202井为算例,将软件计算结果与现场数据进行对比总结。下面分别对2口井的现场应用情况进行分析讨论。
L26-1井为一口致密油水平井,三开井身结构如图 6所示。该井井深为3 467 m,实际垂深为1 770 m,水平段长度为1 432 m,造斜点深度为1 390 m,表层套管下入深度为1 281.49 m,外径为244.5 mm;表层钻头钻进深度为1 282 m,外径为311.2 mm;生产套管下入深度为3 464.15 m,外径为139.7 mm。该井三开水平段采用油基钻井液钻进,钻井液密度为1.14 g/cm3,塑性黏度为28 mPa·s,动切力为15 Pa。为验证摩阻扭矩计算软件的精度,在三开2 224 m处对实际钻井摩阻进行了现场测试。
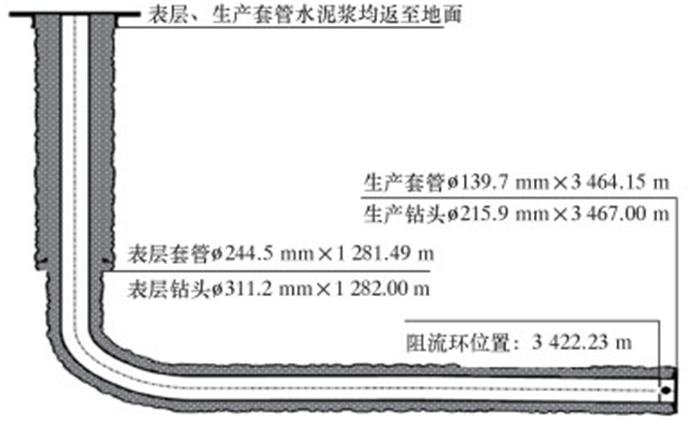
|
| 图 6 L26-1井井身结构图 Fig.6 Borehole configuration of Well L26-1 |
表 1所示为软件在L26-1井的应用结果。计算结果为钻柱扭矩极限2.95 kN·m,释放摩阻45.9 kN,扭摆前沿井深2 224 m,顶驱扭转角度351°,螺杆扭矩3.0 kN·m。现场实际测试数据为2 224 m对应扭矩3.2 kN·m,释放摩阻50.0 kN。扭矩误差为7.81%,摩阻误差为8.20%,均在10%以内。这说明摩阻扭矩计算软件计算精度较高。
| 参数 | 现场数据 | 计算数据 |
| 扭矩极限/(kN·m) | 3.20 | 2.95 |
| 释放摩阻/kN | 50.0 | 45.9 |
D202井是一口页岩气水平井,四开井身结构如图 7所示。

|
| 图 7 D202井井身结构图 Fig.7 Borehole configuration of Well D202 |
该井垂直段钻进方式为顶驱加主轴定位,造斜段为螺杆加顶驱扭摆减阻,水平段为旋转导向工具。在造斜段实施扭摆减阻作业之前,首先通过摩阻扭矩计算软件,结合现场实际钻井数据,对扭摆减阻过程的扭矩极限和扭转角度进行理论计算,计算结果表明:在造斜段实施扭摆减阻钻进的扭矩极限为3.7 kN·m,释放摩阻57.0 kN,扭摆前沿井深3 293 m,顶驱扭转角度744°,螺杆扭矩2.5 kN·m。根据计算结果开展了顶驱扭摆减阻试验,试验井段3 244~3 390 m,井斜从32°上升到64°,扭摆进尺146 m,耗时87 h,平均机械钻速1.68 m/h。在维持立压不变的情况下,实施扭摆减阻后,造斜段“托压”情况明显改善,机械钻速大幅提高。
使用顶驱扭摆减阻技术前,滑动钻进机械钻速为0.40 m/h,使用顶驱扭摆减阻技术后,滑动钻进机械钻速平均达到1.68 m/h,最高达3.40 m/h,试验过程中钻压平稳持续,起钻循环次数显著减少。这充分说明顶驱扭摆减阻技术能够有效降低摩阻,显著提高大斜度井段和水平段钻井效率。
4 结论及认识(1) 滑动钻进过程中,利用顶驱控制上部钻柱往复扭摆,将静摩擦变成动摩擦,可降低滑动钻进钻柱轴向摩擦阻力,消除滑动钻进过程中的托压现象,提高钻井效率。
(2) 所建立的顶驱扭摆减阻模型在现场实际应用结果显示,误差均在10%以内,在可接受范围之内,可以认为计算数据与真实数据误差比较小。因此可以认为笔者建立的顶驱扭摆减阻计算模型较为合理,符合现场实际钻井作业要求,能够为现场作业提供有效指导。
(3) 理论数据与现场数据存在误差可能有以下原因:①简单认为管柱与井眼轴线的形状基本相同;②忽略了弯矩对计算结果的影响;③对钻柱单元进行受力分析时,认为其所受应力全部均匀分布;④软件使用的摩阻扭矩模型建立在二维空间,忽略了方位角对于摩阻扭矩计算结果的影响。
| [1] |
米飞, 张健, 王玉冰. 水平井托压问题原因分析及解决措施[J].
中国石油和化工标准与质量, 2013, 33(10): 181.
MI F, ZHANG J, WANG Y B. Horizontal well backing pressure problems cause analysis and solutions[J]. China Petroleum and Chemical Standard and Quality, 2013, 33(10): 181. DOI: 10.3969/j.issn.1673-4076.2013.10.159 |
| [2] | GILLAN C, BOONE S, KOSTIUK G, et al. Applying precision drill pipe rotation and oscillation to slide drilling problem[R]. SPE 118656, 2009. |
| [3] | MAIDLA E E, HACI M, WRIGHT D. Case history summary: Horizontal drilling performance improvement due to torque rocking on 800 horizontal land wells drilled for unconventional gas resources[R]. SPE 123161, 2009. |
| [4] |
范光第, 黄根炉, 李绪锋, 等. 水平井管柱摩阻扭矩的计算模型[J].
钻采工艺, 2013, 36(5): 22-25.
FAN G D, HUANG G L, LI X F, et al. Calculation model of friction torque for horizontal well string[J]. Drilling & Production Technology, 2013, 36(5): 22-25. |
| [5] |
闫铁, 李庆明, 王岩, 等. 水平井钻柱摩阻扭矩分段计算模型[J].
大庆石油学院学报, 2011, 35(5): 69-72, 83.
YAN T, LI Q M, WANG Y, et al. Segmental calculation model for torque and drag of drillstring in horizontal wells[J]. Journal of Daqing Petroleum Institute, 2011, 35(5): 69-72, 83. |
| [6] |
张林强. 大位移井摩阻扭矩计算模型[J].
断块油气田, 2008, 15(2): 88-91.
ZHANG L Q. Calculating model of torque and drag in extended-reach well[J]. Fault-Block Oil & Gas Field, 2008, 15(2): 88-91. |
| [7] |
郭永峰, 白云程. 国内外钻井摩阻力研究的现状及趋势[J].
国外油田工程, 2001, 17(8): 31-33.
GUO Y F, BAI Y C. The present and trend of study for drilling frictional Resistance written by[J]. Foreign Oilfield Engineering, 2001, 17(8): 31-33. |
| [8] |
张会增, 管志川, 刘永旺, 等. 基于旋转激励的钻柱激振减阻工具的研制[J].
石油机械, 2015, 43(5): 9-12.
ZHANG H Z, GUAN Z C, LIU Y W, et al. Development of drill string excitation drag reduction tool based on rotary excitation[J]. China Petroleum Machinery, 2015, 43(5): 9-12. |



