0 引言
套管柱下入深度设计是井身结构设计中非常重要的一部分。决定套管下入深度的因素有很多,比如地层破裂压力、孔隙压力、井涌余量、岩石性质以及浅层气等。井涌余量是井控过程中确保井控安全的一个参数,它表示在钻井条件下处理井内溢流能力的大小,是评价压井作业安全的重要判据。在井身结构设计过程中,为了保证井身结构安全可靠,在对套管下入深度进行设计时必须考虑井涌余量的影响。
目前,井涌余量的概念缺乏统一的标准[1-10],给井涌余量这一参数的应用带来一定影响。1991年K.P.REDMANN定义井涌余量为井控过程中确保井筒内薄弱层段不被压裂的井筒的最大承压能力[6]。1998年S.OHARA等人将井涌余量定义为允许安全关井而不压裂井筒内薄弱层段的钻井液密度与地层压力当量密度的差值[7];同年O.L.A.SANTOS等也给出了井涌余量定义,即表示为井筒内某一深度发生溢流,能够安全关井,且应用原密度钻井液安全循环溢流排出井筒,而不压裂井筒内薄弱层段(一般为套管鞋位置)的最大井底压力当量钻井液密度与井内压力当量钻井液密度的差值[8]。2011年,CATAK等人定义井涌余量为井筒内某一深度发生溢流,在当时特定的溢流强度下,溢流能够安全循环出井筒,而不压裂井筒内最薄弱层段的最大溢流体积。1983年,国内的郝俊芳定义井涌余量为钻达一定井深时,不压漏井内地层的最大井底压力的当量密度与当时井内钻井液密度的差值,并给出了在压井、无溢流和溢流3种情况下的井涌余量计算公式[9]。1990年国内刘凯根据常规井控,定义井涌余量为在关井和处理溢流过程中允许的最大井底压力当量钻井液密度与正常压井钻井液密度的差值,并给出了不同压井方法的井涌余量计算公式和方法[10]。
笔者主要研究井涌余量对套管下入深度的影响。井涌余量的定义虽然比较多,但是从本质上讲,主要表示在当时井身条件下能够关井和处理溢流的能力。笔者应用O.L.A.SANTOS和R.V.BARRAGAN对井涌余量的定义,根据司钻法压井作业程序,给出了关井和循环排出溢流2个关键阶段井涌余量的计算方法,分别定义为关井井涌余量和循环井涌余量,并应用这2种方法对套管下入深度进行分析和对比,得出一种更合理的应用井涌余量设计套管下入深度的方法。
1 井涌余量计算方法 1.1 关井井涌余量关井井涌余量即为井筒内某一深度发生溢流能够安全关井,而不压裂井筒内薄弱层段(一般为套管鞋位置)的最大井底压力当量钻井液密度与井内压力当量钻井液密度的差值。应用关井法计算井涌余量,首先假设:①侵入井筒的气体在井筒内连续;②不考虑溢流流体的滑移速度;③考虑溢流流体的膨胀;④循环过程中井底压力保持恒定,且为地层压力。关井时,由于停止循环,井内压力当量钻井液密度即为钻井液的密度。
关井井涌余量的计算公式为[8]:
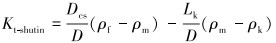
|
(1) |
式中:Kt-shutin为关井井涌余量,g/cm3;D和Dcs分别为井的深度和套管鞋的深度,m;ρf为套管鞋深度Dcs的破裂压力当量密度,g/cm3;ρm和ρk分别为钻井液和溢流流体的密度,g/cm3;Lk为溢流流体在井筒中的高度,m。
1.2 循环井涌余量循环井涌余量定义为井筒内某一深度发生溢流,采用司钻法进行压井过程中,应用原密度钻井液安全循环排出侵入井筒的流体,而不压裂井筒内薄弱层段(一般是套管鞋位置)的最大井底压力当量钻井液密度与井内压力当量钻井液密度的差值。计算公式如下:
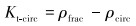
|
(2) |
式中:Kt-circ为循环井涌余量,g/cm3;ρfrac为井筒内薄弱层段的破裂压力当量密度,g/cm3;ρcirc为井筒内薄弱层段的最大循环压力当量密度,g/cm3。
2 套管下入深度设计方法井控过程中,由于气体的可压缩性,井控难度最大,井涌余量计算时,假设溢流流体为气体。井身结构设计过程中,假设套管鞋位置是井筒内薄弱的层段,破裂压力最小。下面分别应用关井井涌余量和循环井涌余量对套管柱下入深度进行设计,设计方法分别简称为关井法和循环法。
2.1 关井法整理式(1)可得出关井时套管鞋深度处的压力当量密度表达式:
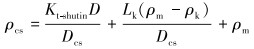
|
(3) |
式中:ρcs为关井时套管鞋处的最大压力当量密度,g/cm3。
在井身结构设计时,井涌余量的取值应不小于发现溢流和关井过程中产生的压力当量密度的变化,以保障井控作业的安全进行。通常把溢流和安全关井而产生的井底压力当量密度的变化称为初始井涌余量。在井身结构设计过程中,初始井涌余量的取值一般根据井控技术水平来确定,钻井过程中所使用的钻井设备的溢流监测能力和钻井人员及井控设备的响应能力越强,初始井涌余量的取值越小。依据石油天然气行业标准《井身结构设计方法》,采用自下而上的套管下入深度设计方法[11],具体如下。
(1) 确定孔隙压力与破裂压力的压力梯度剖面。
(2) 根据某一层段的井深D,确定此深度的孔隙压力、钻井液密度、初始井涌余量和溢流流体密度。
(3) 假设套管鞋深度Dcs。
(4) 根据式(3)计算套管鞋Dcs处所允许的最大压力当量密度。
(5) 确定套管鞋Dcs处的地层的破裂压力当量密度。
(6) 比较第4步和第5步计算的压力当量密度值。如果相等或最大压力当量密度略小于破裂压力当量密度,则假设的深度为套管的下入深度;如果不等,重复第3步计算,重新假设新的套管下入深度,直到相等为止。
2.2 循环法采用司钻法循环排气的过程中,溢流气体到达套管鞋位置时,套管鞋处的循环压力最大。应用气液两相流理论来计算循环排气过程中,套管鞋位置处压力的变化。计算过程中考虑了循环排气过程中气体的膨胀和滑移效应,也考虑了两相流流动的摩阻压耗。
溢流气体和钻井液的连续性方程为:
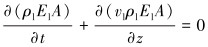
|
(4) |
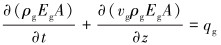
|
(5) |
气体和钻井液的动量守恒方程为:
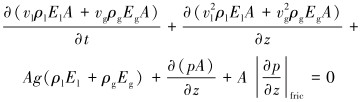
|
(6) |
式中:ρl和ρg分别为钻井液和气体的密度,kg/m3;El和Eg为钻井液和产出气的体积分数;vl和vg分别为钻井液和气体的速度,m/s;A为环空截面积,m2;qg为单位厚度产出气的质量流量,kg/(s·m);p为压力,Pa。
根据气体产能方程,可得到单位时间、单位厚度气侵质量[12]为:
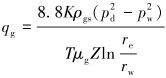
|
(7) |
式中:K为气相渗透率,μm2;μg为天然气黏度,mPa·s;Z为天然气压缩系数;T为气层温度,K;re为供油半径,m;rw为井眼半径,m;pd为地层压力,MPa;pw为井底压力,MPa。
当循环排气时,通过调节井口的节流阀施加回压平衡地层压力,地层流体不再进入,此时qg=0。
采用有限差分方法对气液两相流控制方程求解,整个环空设定为空间域,从正常循环至气体排出井口这个时间段设定为时间域。通过有限差分对数学模型进行离散,将原数学模型在定解域上的解转化为在定解域中网格节点上的离散解,通过迭代循环求得不同时间域和空间域上各节点的值,再求得任意时刻任意未知的压力[13-14],进而求得气体前缘到达套管鞋位置时套管鞋位置承受的最大压力pcs-circ。
根据计算的套管鞋处的最大压力计算套管鞋处的最大循环压力当量密度:
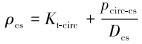
|
(8) |
套管下入深度的设计同关井法一样,依据石油天然气行业标准《井身结构设计方法》,采用自下而上的套管下入深度设计方法。如果计算的最大循环压力当量密度与地层破裂压力当量密度相等或略小于破裂压力当量密度,则假设的深度为套管的下入深度;如果不等,则重复计算。
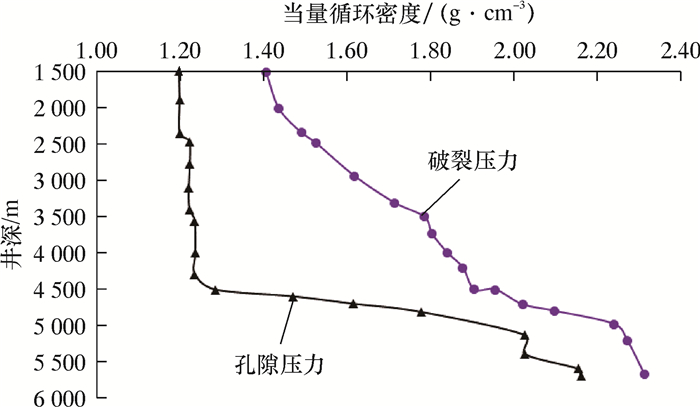
3 算例分析采用文献[15]中一口深水井的孔隙压力和破裂压力曲线进行算例分析,该井设计目的深度为5 700 m。应用关井法和循环法对套管下入深度进行设计。该深水井的孔隙压力和破裂压力的压力剖面如图 1所示。
|
| 图 1 孔隙压力梯度和破裂压力梯度随井深变化关系 Fig.1 The pore pressure and fracture pressure ECD profile |
3.1 设计方法对比
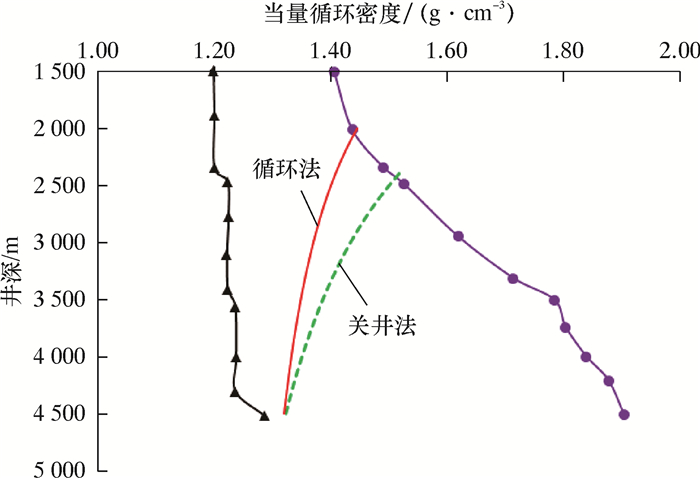
应用该深水井的压力剖面对ø177.8 mm套管的下入深度进行设计。表 1为ø177.8 mm套管下入深度设计参数。假设初始井涌余量为0.05 g/cm3,分别应用关井法和循环法确定套管的下入深度,如图 2所示。
| 目标深度/m | 井涌余量/(g·cm-3) | 地层渗透率/(10-3μm2) | 气体的相对密度* | 钻井液密度/(g·cm-3) | 钻井液黏度/cP | 钻杆外径/m | 井筒内径/m | 钻井液排量/(L·s-1) |
| 4 500 | 0.05 | 800 | 0.7 | 1.32 | 10 | 0.127 | 0.158 75 | 1.58 |
| *注:该密度为相对于空气的密度。 | ||||||||
|
| 图 2 应用关井法和循环法确定ø177.8 mm套管的下入深度 Fig.2 Application of shut-in method and circulation method to determine the setting depth of ø177.8 mm casing |
从图 2可知,在相同井涌余量情况下,应用关井法确定的套管下入深度要比循环法确定的下入深度深,即单层套管柱的下入长度较短。关井法计算相对简单,计算结果偏于保守,在一定程度上增加了井身结构设计的安全性,但同时也增加了钻井成本。
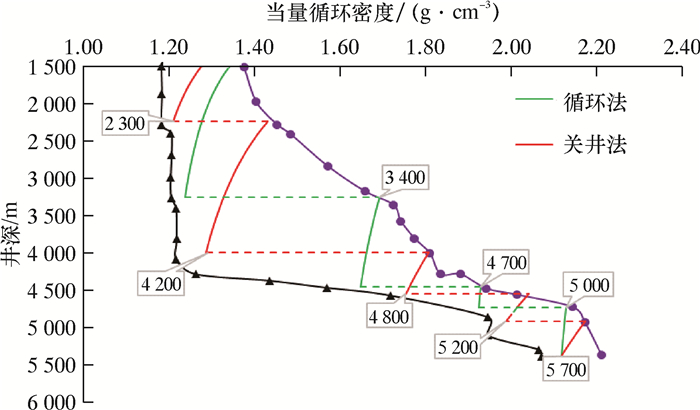
根据该深水井的孔隙压力和破裂压力曲线,应用关井法和循环法对该井的井身结构进行设计。设计参数如表 2所示。假设每层套管设计时应用的井涌余量取值相同,分别应用关井法和循环法对套管的下入深度进行设计,结果如图 3所示。
| 套管外径/mm | 井涌余量/(g·cm-3) | 地层渗透率/(10-3μm2) | 气体的相对密度* | 钻井液密度/(g·cm-3) | 钻井液黏度/cP | 钻杆外径/m | 井筒内径/m | 排量/(m3·min-1) |
| 177.8 | 0.05 | 800 | 0.7 | 2.160 | 10 | 0.127 | 0.158 75 | 1.58 |
| 244.5 | 0.05 | 800 | 0.7 | 2.040 | 10 | 0.127 | 0.215 90 | 1.58 |
| 339.7 | 0.05 | 800 | 0.7 | 1.860 | 10 | 0.127 | 0.279 40 | 1.58 |
| 406.4 | 0.05 | 800 | 0.7 | 1.198 | 10 | 0.127 | 0.374 65 | 1.58 |
| *注:该密度为相对于空气的密度。 | ||||||||
|
| 图 3 关井法与循环法设计结果对比 Fig.3 Comparison of design results of shut-in method and circulation method |
从图 3可以看出,应用关井法对套管下入深度进行设计,由于单层套管的下入深度减少,套管层次增加,设计结果需要5层套管才能钻达目的深度;而循环法可以有效延长单层套管的下入深度,只需要4层套管便能钻达设计深度。井身结构设计时,应用循环法可减少套管层次,使设计的井身结构更加经济。
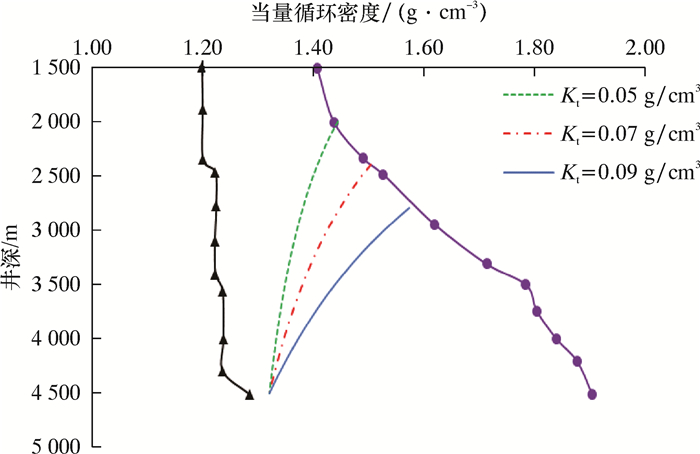
3.2 影响因素分析 3.2.1 初始井涌余量对套管下入深度的影响采用表 1中的数据,改变初始井涌余量Kt,分别设为0.05、0.07和0.09 g/cm3,应用循环法计算套管的下入深度,计算结果如图 4所示。
|
| 图 4 初始井涌余量对套管下入深度的影响 Fig.4 Effect of initial kick tolerance on casing setting depth |
从图 4可以看出,初始井涌余量的设定对套管的下入深度有着非常重要的影响。初始井涌余量越大,套管鞋的深度越深,即单层套管的下入深度越小。初始井涌余量的取值与钻井过程中发现溢流到关井侵入井筒流体的体积有关。初始井涌余量越大,能够处理的侵入井筒流体体积越大,井控安全性越高。在钻井过程中,设备监测溢流的能力、作业人员的操作水平和井控设备的响应时间都决定了发现溢流时侵入井筒流体体积的大小,因此应尽可能提高钻井设备的溢流监测能力和钻井人员及井控设备的响应能力,这样可以有效减小侵入井筒流体体积,减小初始井涌余量,延长单层套管的下入深度。另外,侵入井筒流体体积与井涌强度、油气层暴露面积有关,进入储层段后应尽量控制机械钻速,提醒工作人员密切关注溢流征兆,一旦发生溢流,应及时做出反应,尽量减小溢流的体积。
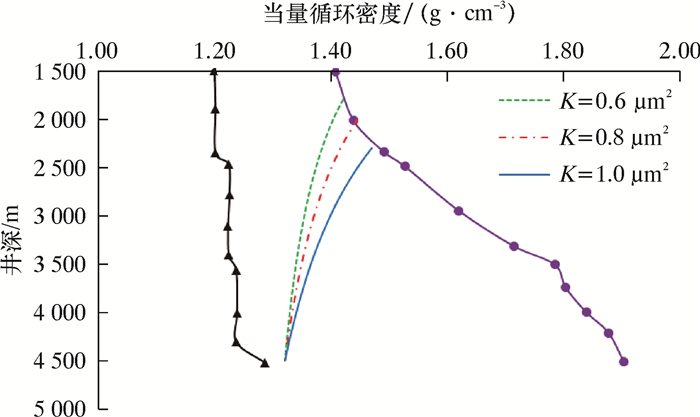
3.2.2 地层渗透率对套管下入深度的影响采用表 1的数据,假设初始井涌余量为0.05 g/cm3,井底负压差为1 MPa,地层渗透率K分别为0.6、0.8和1.0 μm2时,应用循环法计算套管的下入深度,计算结果如图 5所示。
|
| 图 5 地层渗透率对套管下入深度的影响 Fig.5 Effect of formation permeability on casing setting depth |
从图 5可以看出,在相同井涌余量和井底压差的情况下,地层的渗透率对套管的下入深度也产生影响。地层渗透率越大,单层套管的下入深度越小;地层渗透率越小,单层套管的下入深度越大。应用循环法计算井涌余量对套管下入深度进行设计时,除了要考虑侵入井筒内流体体积的影响外,还要考虑所钻地层的物性参数影响,特别是高渗气层,要准确预测地层的渗透率,从而获得更精确的井涌余量,使套管的下入深度设计更为安全可靠。
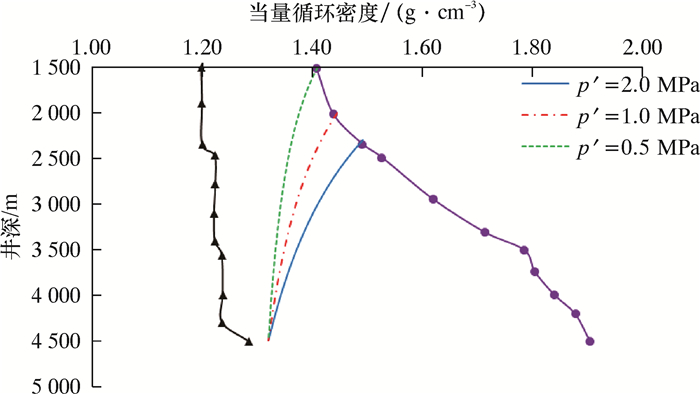
3.2.3 初始井底压差对套管下入深度的影响采用表 1的数据,假设初始井涌余量为0.05 g/cm3,地层渗透率为0.8 μm2,改变井底负压差p′分别为0.5、1.0和2.0 MPa,应用循环法计算套管的下入深度,计算结果如图 6所示。
|
| 图 6 初始井底压差对套管下入深度的影响 Fig.6 Effect of initial bottomhole pressure difference on casing setting depth |
从图 6可以看出,在初始井涌余量和地层渗透率取值相同的情况下,初始井底负压差越大,套管的下入深度越深,即单层套管的下入深度越小。因此在应用循环法对套管柱下入深度进行设计前,应尽量准确预测地层的孔隙压力,减小由于孔隙压力预测误差而引起的井下复杂情况,延长单层套管的下入深度。
通过以上分析可知,从钻井安全角度讲,关井法相比循环法更加安全,如果对所钻地层层段不是很了解,推荐应用关井法对套管柱下入深度进行设计。循环法虽然可以延长单层套管的下入深度,使设计的井身结构更加经济,但是应用前需要对所钻地层的物性参数进行精确预测,如储层渗透率和地层孔隙压力等,因此该方法比较适用于勘探成熟的区块。对所钻层位比较熟悉,或已获得所钻层位的物性参数,可应用循环法对套管柱的下入深度进行设计和优化。
4 结论(1) 根据井控作业程序,采用关井和循环排出溢流2个关键阶段的井涌余量计算方法,得出了2种套管下入深度的设计方法,分别为关井法和循环法。
(2) 通过案例仿真分析,对比了关井法和循环法对套管下入深度设计的影响。关井法计算结果偏于保守,单层套管下入深度较小,安全性较高;循环法计算结果较为精确,可以有效增加单层套管下入深度,减少套管层次,比较经济。
(3) 循环法具有较高的设计精度,但需要对所钻地层物性参数进行精确预测,才能保证设计的可靠性,因此该方法比较适用于对勘探成熟的区块进行井身结构优化。
| [1] | SANTOS O L A, MENDES J R P, RIBEIRO P R. The development and application of a software to assist the drilling engineer during well control operations in deep and ultra deep waters[R]. SPE 81184, 2003. |
| [2] | SANTOS H M, CATAK E, VALLURI S. Kick tolerance misconceptions and consequences to well design[R]. SPE 140113, 2011. |
| [3] | UMAR L, THIAM Y Y, MURAD M S B A, et al. Dynamic multiphase kick tolerance allows safe drilling which led to huge gas discovery in a HPHT exploration well in Malaysia[R]. IPTC 17460, 2014. |
| [4] | NORDIN N A, UMAR L, AZIZ I A B A, et al. Dynamic modeling of wellbore pressures allows successful drilling of a narrow margin HPHT exploration well in Malaysia[R]. SPE 155580, 2012. |
| [5] | REDMANN JR K P. Understanding kick tolerance and its significance in drilling planning and execution[J]. SPE Drilling Engineering, 1991, 6(4): 245-249. DOI: 10.2118/19991-PA |
| [6] | SANTOS O, ADASANI I, AZAR J J, et al. Determination of casing setting depth using kick tolerance concept[R]. SPE 30220, 1995. |
| [7] | OHARA S, BOURGOYNE JR A T. Circulating kick tolerance for deep water drilling[C]//IADC, well control conference of the Americas, caracas, Venezuela, 1998. |
| [8] | SANTOS O L A, BARRAGAN R V. Well control concepts used for planning and executing deep water wells[C]//IADC Deep Water Well Control Conference, Houston, TX, OSA, 1998. |
| [9] |
郝俊芳. 如何计算井涌余量[J].
西南石油学院学报, 1983(3): 45-50.
HAO J F. How to calculate kick tolerance[J]. Journal of Southwest Petroleum Institute, 1983(3): 45-50. |
| [10] |
刘凯. 如何认识和计算井涌余量[J].
西南石油学院学报, 1990, 12(1): 37-45.
LIU K. How to recognize and calculate kick tolerance[J]. Journal of Southwest Petroleum Institute, 1990, 12(1): 37-45. |
| [11] |
中华人民共和国国家发展和改革委员会. 井身结构设计方法: SY/T 5431-2008[S]. 北京: 石油工业出版社, 2008. National Development and Reform Commission. The design method of casing program: SY/T 5431-2008[S]. Beijing: Petroleum Industry Press, 2008. |
| [12] |
宋荣荣, 孙宝江, 王志远, 等. 控压钻井气侵后井口回压的影响因素分析[J].
石油钻探技术, 2011, 39(4): 19-24.
SONG R R, SUN B J, WANG Z Y, et al. Analysis of the influence factors of wellhead back pressure in managed pressure drilling after gas invasion[J]. Petroleum Drilling Techniques, 2011, 39(4): 19-24. |
| [13] | CHOI J, PEREYRA E, SARICA C, et al. An efficient drift-flux closure relationship to estimate liquid holdups of gas-liquid two-phase flow in pipes[J]. Energies, 2012, 5(12): 5294-5306. DOI: 10.3390/en5125294 |
| [14] | CHOI J, PEREYRA E, SARICA C, et al. Development of a fast transient simulator for gas-liquid two-phase flow in pipes[J]. Journal of Petroleum Science and Engineering, 2013, 102: 27-35. DOI: 10.1016/j.petrol.2013.01.006 |
| [15] | LAGE A C V M, NAKAGAWA E Y, ROCHA L A S, et al. New methodology for design of casing setting depth and drilling follow-up[R]. SPE 36102, 1996. |



