0 引言
由于油田采出液含水量较高,同时油田回注水需求量大,目前各油田主要采用化学法和物理法等一些常规油水分离方法[1-2]。考虑污染程度及成本问题,多数处理方法选择物理分离较多,而螺旋管以其结构简单和生产方便等优点适用于石油化工及动力工程等核心领域,其机理运用涉及多相流动和传热交换等诸多方面[3]。螺旋管的结构形状对管内流体流动方式、相变应力及传热特性有着重要影响,同时也直接影响相应配套设备的安全性及高效性[4]。
国内外相关学者对螺旋管的油水两相流动中不同工况下的湍流强度及油滴聚结浮升等做了大量研究,发现相比于水力旋流器的高速离心分离,螺旋管可以在一定程度上将受到重力密度差及离心力的小粒径油滴离散油相聚结,并上升至管内上壁面形成油膜,然后随着流体流动不断滑移聚结直至流出管口。李广军等[5]对立式、卧式螺旋管内油水两相流动的流型变化进行了试验研究。龚道童等[6]对带孔螺旋管的变质量流动进行了模拟研究。华正荣[7]模拟了不同工况下螺旋管的分离效果并与实际试验中的数据进行对比。周云龙等[8]研究了改变矩形截面螺旋管的螺旋直径及升角对气液两相的流行变化。
笔者以水和油为混合介质,运用Euler-Euler多相流模型及PBM相群平衡方程对螺旋管内油水两相流动进行数值模拟,研究了圆形螺旋管在混合液入口流速为0.10~0.50 m/s范围内与在同一速度不同回转形状下管内油水分离效果及两相分布规律,以期为螺旋管结构形状的优化设计提供参考。
1 模型建立 1.1 物理模型使用PROE软件建立回转形状为圆形的基础螺旋管模型,模型沿Y轴竖直放置,回转半径500 mm,螺距100 mm,管径20 mm,圈数为10。其他3种不同回转形状基于圆形进行绘制,4种螺旋管的回转形状几何模型如图 1所示。
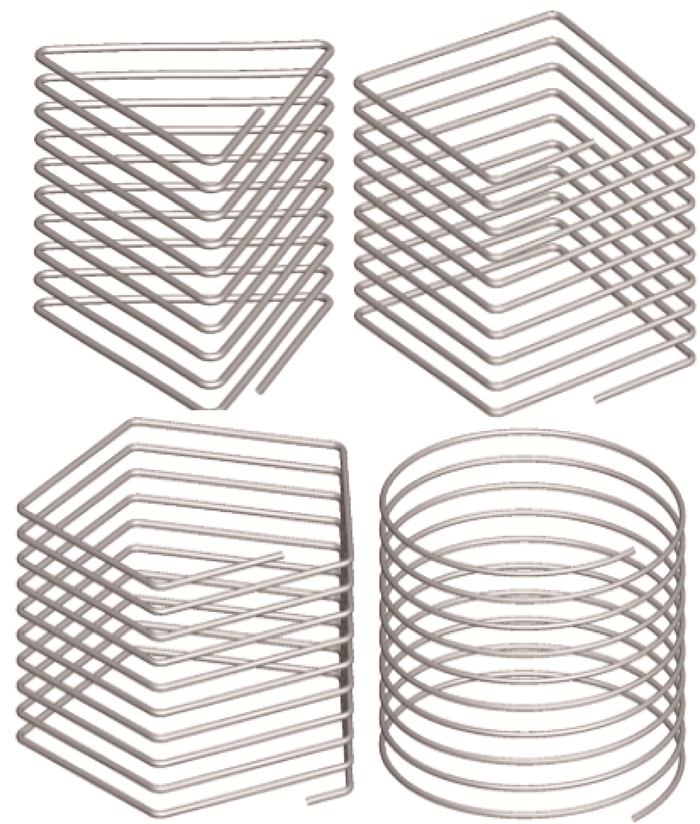
|
| 图 1 4种回转形状几何模型 Fig.1 Geometric model for 4 kinds of spiral shape |
考虑螺旋管曲率及弯曲,使用四面体网格划分方法Tetrahedrons及高级网格划分方式Proximity and Curvature方法划分4种螺旋管,网格结构如图 2所示。
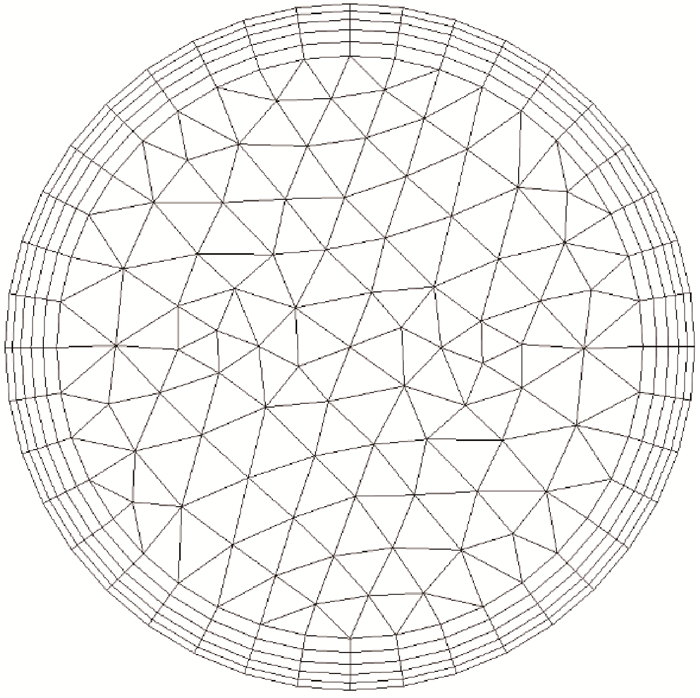
|
| 图 2 网格结构 Fig.2 Grid structure |
4种回转形状螺旋管的具体网格数及网格质量见表 1。
| 回转形状 | 圆形 | 三角形 | 四边形 | 五边形 |
| 网格数 | 110万 | 105万 | 107万 | 109万 |
| 网格质量 | >0.4 | >0.2 | >0.3 | >0.3 |
1.2 边界条件
油水混合物选用流型与油-水两相的相对表观速度有关,笔者因选用流型为带有混合层的分层流,油相初始体积分数为20%,所以选用上入口为速度入口、下出口为自由出口。先以原型螺旋管确定相对较优的入口速度,再以此速度对比模拟不同回转形状下螺旋管内油水分层情况,其具体模拟参数设定见表 2。螺旋管内壁面设定为无滑移边界,壁面粗糙度沿用默认值0.5。
| 压力/Pa | 油滴粒径/mm | 水相密度/(kg·m-3) | 水相动力黏度/(Pa·s) | 油相密度/(kg·m-3) | 油相动力黏度/(Pa·s) |
| 101 325 | 0.1 | 998.2 | 0.001 003 | 889 | 1.06 |
1.3 数值模型选用 1.3.1 多相流模型
将螺旋管内油-水两相流动过程简化设定为恒温恒压体系,不涉及能量交换。因为需要考虑混合流体内两相的相对滑移及相间拽力,采用Euler-Euler多相流模型进行模拟,模拟涉及管内油-水两相间的相互作用,通过连续方程及动量方程计算求解油-水两相分离情况,并利用压力项和界面交换系数实现相间的耦合。
管流连续方程:
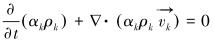
|
(1) |
管流动量方程:
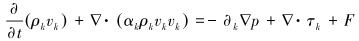
|
(2) |
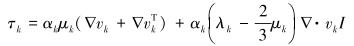
|
(3) |
式中:t为时间,αk为k相体积分数,g为重力加速度,ρk为k相密度,μk为k相湍流黏度,vk为k相速度,τk为k相应变张量,F为相间的相互作用,λk为k相体积黏度,T为应力矢量,I为应力张量的不变量。
1.3.2 湍流模型混合流体在螺旋管内会随着旋流流动产生较大的湍流能量及耗散率,因此选用湍流模型中的RNG k-ε湍流模型,可以在计算中考虑实际两相黏性分层流动,同时对螺旋管内的旋流状况进行模拟修正[9]。
1.3.3 相群平衡模型为考虑液液乳化分离中油滴粒径在两相流动中的增长、聚合及破碎状况,在考虑动量和质量守恒方程的基础上,还添加了ANSYS FLUENT内置平衡方程来描述粒子运动平衡,此方程称为相群平衡方程(PBM)。考虑只有油相一种离散相,所以选用均一离散法模拟计算粒径间隔,通过对油滴粒径变化情况的考量,模拟油水两相在螺旋管中油滴的聚结与油水分离的状况。
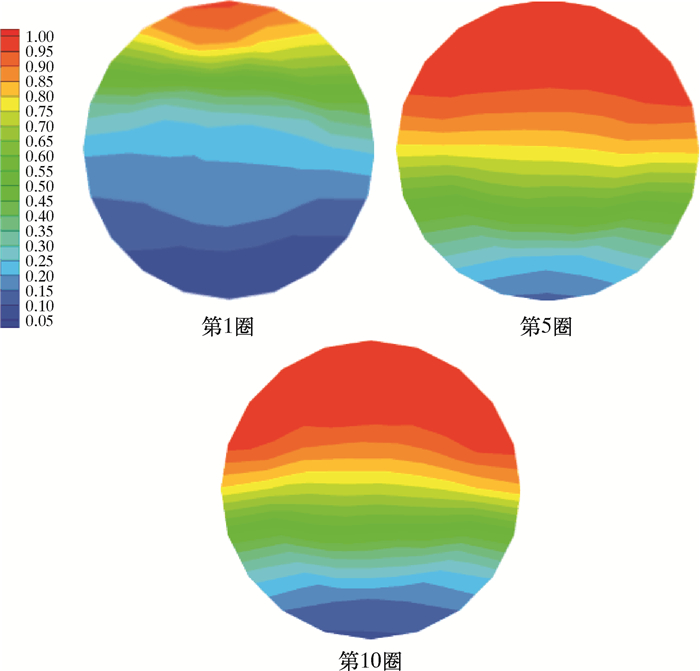
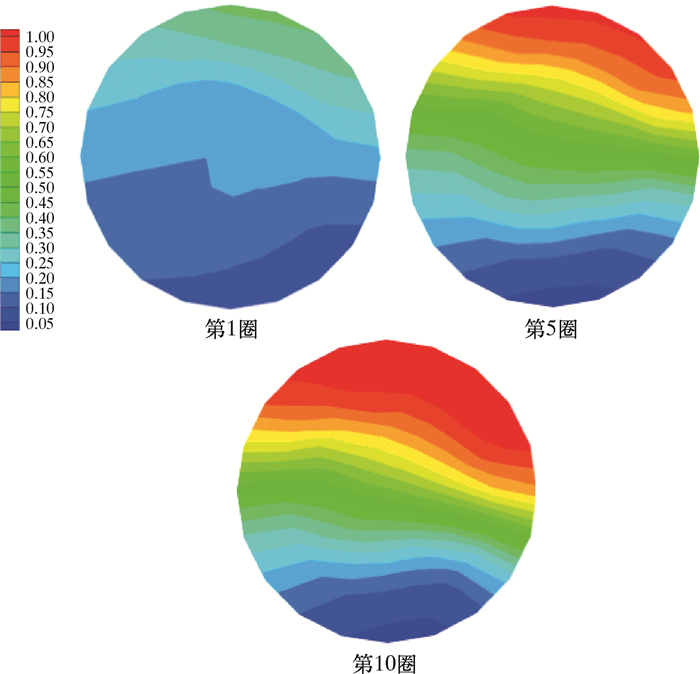
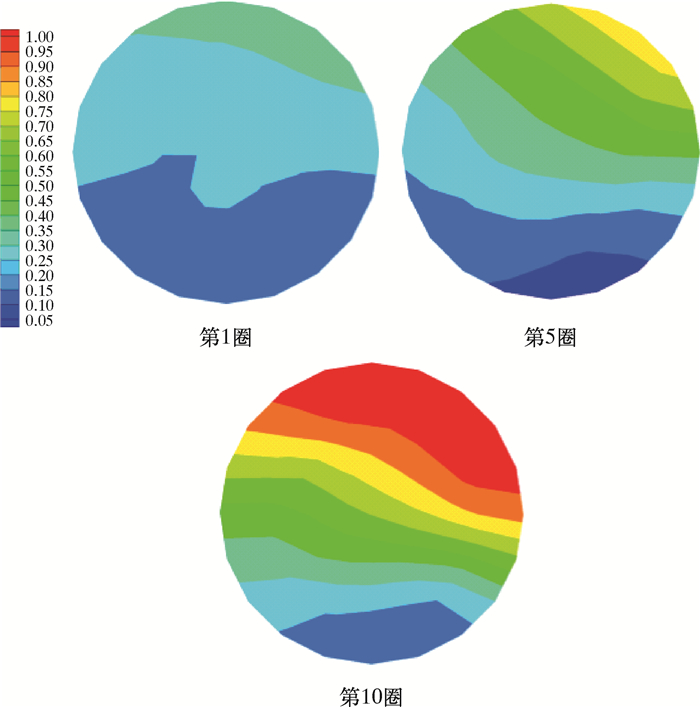
2 螺旋管内油水两相模拟结果分析 2.1 圆形螺旋管不同流速下两相模拟分析为优化选择最佳的分离效果模型,对比分析入口流速的变化对分离效果的影响。通过直接设定不同的入口速度模拟入口流量,并将模拟结果云图进行分析总结。入口流速为0.10、0.25、0.30、0.40和0.50 m/s下的螺旋管XY平面截图下的油相体积分数分布云图分别如图 3~图 7所示。
|
| 图 3 入口流速为0.10 m/s时油相体积分数分布云图 Fig.3 The oil phase volume fraction distribution under the inlet flow rate of 0.10 m/s |
|
| 图 4 入口流速为0.25 m/s时油相体积分数分布云图 Fig.4 The oil phase volume fraction distribution under the inlet flow rate of 0.25 m/s |
|
| 图 5 入口流速为0.30 m/s时油相体积分数分布云图 Fig.5 The oil phase volume fraction distribution under the inlet flow rate of 0.30 m/s |
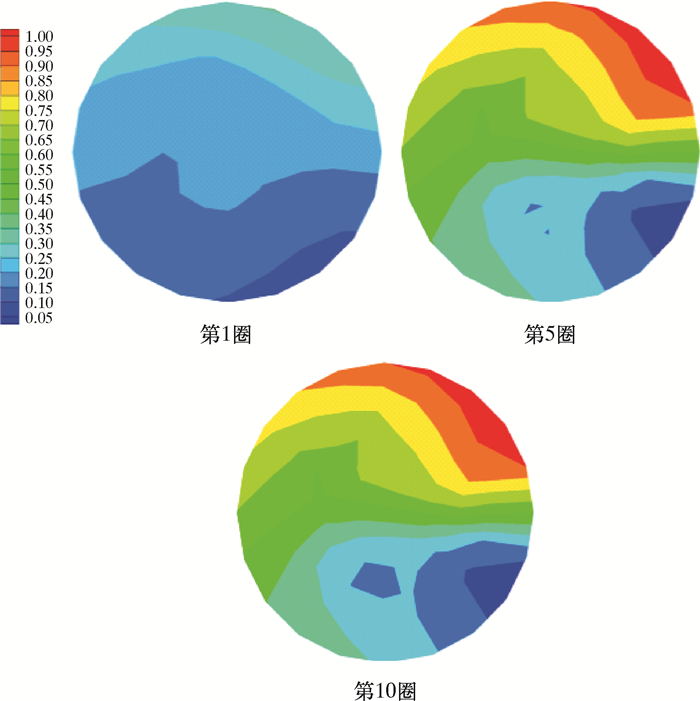
|
| 图 6 入口流速为0.40 m/s时油相体积分数分布云图 Fig.6 The oil phase volume fraction distribution under the inlet flow rate of 0.40 m/s |
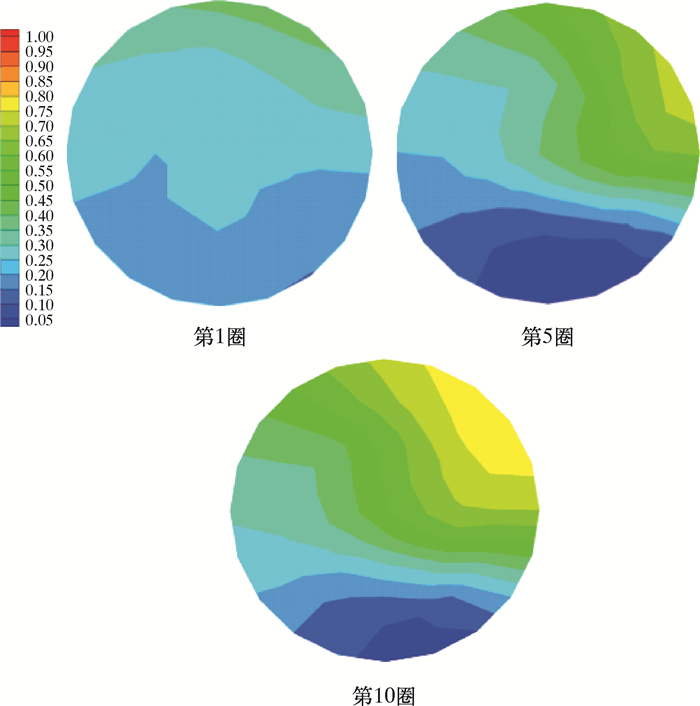
|
| 图 7 入口流速为0.50 m/s时油相体积分数分布云图 Fig.7 The oil phase volume fraction distribution under the inlet flow rate of 0.50 m/s |
螺旋管中油水两相受离心力与重力影响,从第1圈逐渐开始分离,随着回转圈数的增加,油相渐渐聚结浮升至右上角,油相体积分数增加,并且在第10圈达到稳定。通过图 3到图 7对不同速度下油相体积分数云图对比分析发现,改变入口流速对整体的模拟结果变化显著。当入口流速为0.10 m/s时,油水分离主要受到重力影响,分离界面不明显且层数较多,油相体积分数不高。当入口流速为0.25 m/s时,分离受到离心力与重力共同作用,油水分离效果较好,但是分离界面层数较多。当入口流速为0.30 m/s时,油水混合物分离明显且界面分布清晰、层数较少,分离效果最佳。当入口流速为0.40和0.50 m/s时,随着入口流速加快,油水分离效果逐渐减弱。
理论上,随着入口流速加快,油相受到的离心力越大,分离效果越好。可实际上流速的加快伴随着油水混合物在管中停留时间的缩短,致使重力分离影响降低,同时湍动能的增大会阻止油滴的聚结,甚至使油滴破碎。不过在实际流动分离中还需考虑分离时效,加快分离时间。
综上所述,结合模拟几何模型选择的最佳入口流速为0.30 m/s。
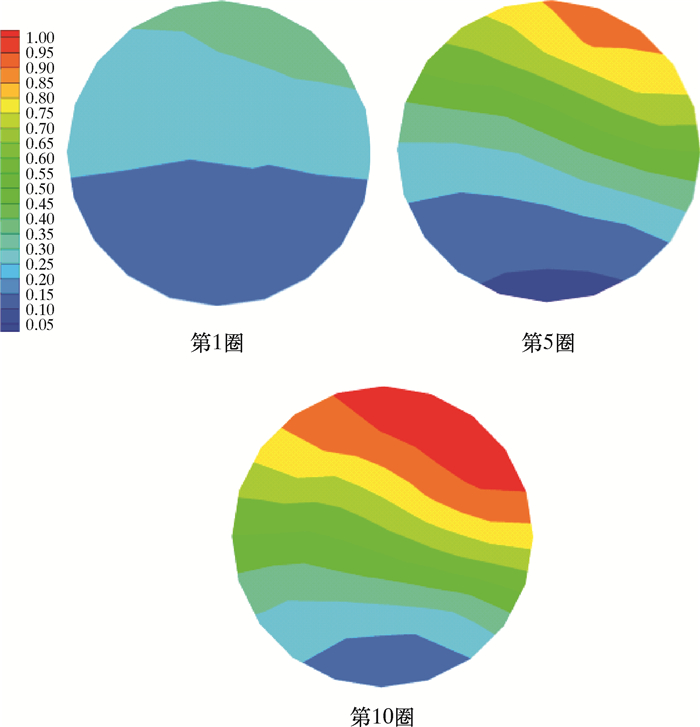
2.2 不同回转形状下两相模拟对比分析在截取选择圆形回转形状的最佳入口流速后,模拟在入口流速为0.30 m/s时,另外3种回转形状的油水分离情况,并得到同等位置下XY平面截图下的油相体积分数分布云图,结果如图 8~图 10所示。
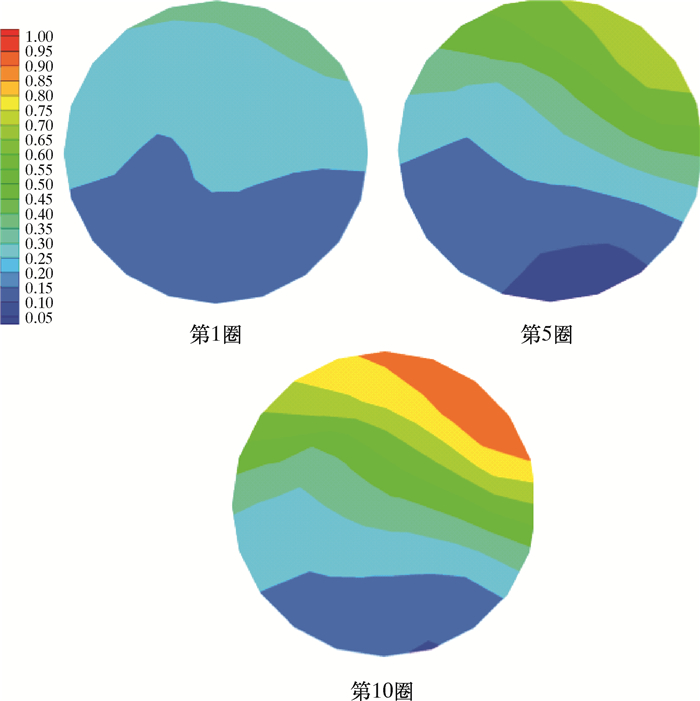
|
| 图 8 三角形回转入口流速为0.30 m/s时油相体积分数分布云图 Fig.8 The oil phase volume fraction distribution under the inlet flow rate of 0.30 m/s in the triangle rotary shape spiral pipe |
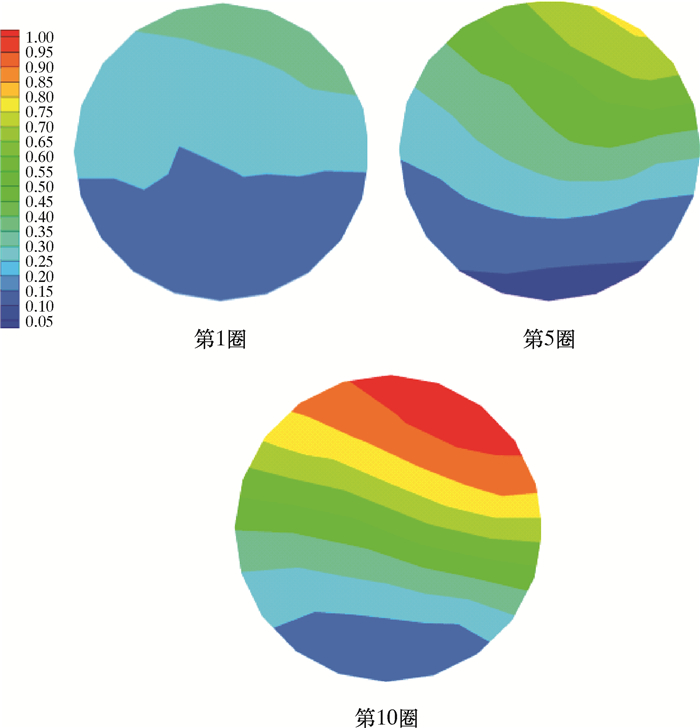
|
| 图 9 四边形回转入口流速为0.30 m/s时油相体积分数分布云图 Fig.9 The oil phase volume fraction distribution under the inlet flow rate of 0.30 m/s in the quadrangular rotary shape spiral pipe |
|
| 图 10 五边形回转入口流速为0.30 m/s时油相体积分数分布云图 Fig.10 The oil phase volume fraction distribution under the inlet flow rate of 0.30 m/s in the pentagonal rotary shape spiral pipe |
同一流速下,随着回转边数的增多,其油水分离效率及分离程度都随之加强。从图 8到图 10可以看出,减少回转角度并没有提升油滴的撞击聚结概率,而增加回转边数,即增加回转流动次数能提高螺旋管的整体油水分离效率。与其他3种回转形状相比,圆形回转形状相当于拥有无数条回转边数的几何多边形状,所以其提高了油水混合液中油滴的聚结概率从而加强大油滴的生成及浮升,最终达到提升油水分离效率的目的。
3 结论(1) 对于圆形回转形状的螺旋管,当入口流速过低,油水分离相当于只受重力沉降影响,分离效果不佳。而当入口流速增加直至到最优值的这一范围内,其分离效果逐步加强、分层明显。但是当入口流速超过最优值,其分离效果将逐渐减弱。基于笔者建立的几何模型,其相对较佳入口流速为0.30 m/s。
(2) 对于非圆形回转形状的螺旋管,在其他几何参数相同的情况下,随着回转边数的增多,螺旋管的分离效果随之增强。相对于另外3种回转形状,圆形回转形状螺旋管分离效果最好,油水分层也较为明显。
| [1] |
罗彩龙, 朱琴. 国内油田含油污水处理现状与展望[J].
石油和化工设备, 2010, 13(11): 55-57.
LUO C L, ZHU Q. Current situation and prospect of oily wastewater treatment in domestic oil fields[J]. Petro & Chemical Equipment, 2010, 13(11): 55-57. DOI: 10.3969/j.issn.1674-8980.2010.11.016 |
| [2] |
任永忠, 陈素宁, 刘智金, 等. 油田外排污水处理技术及研究进展[J].
安全与环境工程, 2011, 18(2): 45-48, 64.
REN Y Z, CHEN S N, LIU Z J, et al. Treatment technology of oilfield discharged wastewater and development tendency[J]. Safety and Environmental Engineering, 2011, 18(2): 45-48, 64. |
| [3] |
朱建国, 仇性启. 螺旋管技术研究[J].
工业加热, 2004, 33(1): 13-17.
ZHU J G, QIU X Q. Technical researches on spiral tube[J]. Industrial Heating, 2004, 33(1): 13-17. |
| [4] |
张小艳, 姜芳芳. 螺旋管换热技术的研究现状综述[J].
制冷与空调(四川), 2014, 28(1): 75-80.
ZHANG X Y, JIANG F F. Present situation of the technical research on spiral tube[J]. Refrigeration & Air Conditioning, 2014, 28(1): 75-80. |
| [5] |
李广军, 郭烈锦, 高晖, 等. 螺旋管内油-水液液两相流流型[J].
化工学报, 2000, 51(2): 239-242.
LI G J, GUO L J, GAO H, et al. Flow patterns of oil-water liquid-liquid two-phase flow in hellcally coiled tubes[J]. Journal of Chemical Industry and Engineering(China), 2000, 51(2): 239-242. |
| [6] |
龚道童, 吴应湘, 郑之初, 等. 变质量流量螺旋管内两相流数值模拟[J].
水动力学研究与进展A辑, 2006, 21(5): 640-645.
GONG D T, WU Y X, ZHENG Z C, et al. Numerical simulation of the oil-water two-phase flow in a helical tube with variable mass flow rates[J]. Journal of Hydrodynamics, 2006, 21(5): 640-645. |
| [7] |
华正荣. 螺旋管分离技术研究[D]. 大庆: 大庆石油学院, 2009. HUA Z R. Study on helical coil separating technology[J]. Daqing: Daqing Petroleum Institute, 2009. |
| [8] |
周云龙, 张立彦. 矩形截面螺旋管内气液两相流型转换数值模拟[J].
化工学报, 2014, 65(12): 4767-4774.
ZHOU Y L, ZHANG L Y. Numerical simulation of flow pattern transition for gas-liquid two-phase flow in helical square ducts[J]. CIESC Journal, 2014, 65(12): 4767-4774. |
| [9] | ZHAO L X, XU B R, JIANG M H, et al. Flow-field distribution and parametric-optimisation analysis of spiral-tube separators[J]. Chemical Engineering Research and Design, 2012, 90(8): 1011-1018. DOI: 10.1016/j.cherd.2011.11.014 |




