0 引言
水力压裂是油气井增产的重要手段之一。水力裂缝为油气藏提供了油气输运通道,改善了储层的油气渗流特性[1]。人工裂缝间距是影响水平井压裂效果的重要因素之一,随着水平井分段压裂级数的不断增加,合理的裂缝间距布置可避免裂缝间的应力干扰,提高油气藏产能。而水力裂缝应力受到相邻裂缝及外界力的干扰[2],随着流体经由裂缝进入地层,水力裂缝周围的应力场可能会发生转向,并最终影响水力裂缝的延伸和周围应力分布[3]。因此,研究水力裂缝周围应力场可以为水平井水力分段压裂的裂缝布置提供理论依据。
国外对于裂缝周围应力分布做了很多研究。I.N.SNEDDON等[4]得到了在不考虑地应力条件下的水平裂缝周围应力分布,发现裂缝的应力沿裂缝对称分布;N.P.ROUSSEL等[5]利用三维数值模型研究了单条和多条裂缝之间的应力干扰,采用位移不连续法控制裂缝的形态和应力,在假设裂缝为理想条件(不发生倾斜)下,通过3条裂缝模型来模拟均质地层中的裂缝应力干扰及裂缝延伸。国内对裂缝周围应力研究主要集中在不同状态下,裂缝端部周围的应力强度因子的变化规律[6]。汤连生等[7]推导得到在静水压力和动水压力作用下岩体中倾斜裂缝端部断裂因子及裂缝断裂准则;王元汉等[8]通过推导得到了裂缝在拉剪及压剪应力状态下端部应力强度因子的变化规律。在石油岩石力学方面,应力场研究主要集中在井筒内部,没有延伸到地层中[9]。姜浒等[10]针对套管射孔改变井眼周围应力,分析了直井水力压裂裂缝周围应力分布;张广清等[11]建立了水平井水力裂缝的空间转向延伸模型,研究了井筒中的应力分布规律。回顾国内外现有的研究成果,并没有对Ⅰ-Ⅱ型水力裂缝的周围应力场形态以及分布机理进行深入的分析。
笔者基于势理论推导得到无限大地层水力裂缝周围应力场解析模型,利用应力叠加原理,建立了考虑地应力和缝内流体压力共同作用下倾斜裂缝周围应力场解析式,并对4种不同倾角下水力裂缝周围应力场分布规律进行了分析,得出水力裂缝周围应力的变化规律以及诱导应力的影响范围。研究结果可为水平井射孔角优选以及分段压裂的裂缝优化布置提供一定的理论指导。
1 Ⅰ-Ⅱ型复合裂缝周围应力数学模型水力裂缝在加载条件下,裂隙面处于拉剪应力状态,目前国内外的研究重点主要是拉剪应力状态下的裂缝端部应力强度因子计算及断裂准则推导,对于拉剪应力条件下无限大平面内单条水力裂缝周围应力场的分析较少。笔者假设裂缝处于无限大平面内,周边岩体均为线弹性体,运用势理论计算得到单条裂缝周边应力场,由westergaard应力函数推导得到拉剪应力作用下裂缝周边的应力场分布,分析该应力场的扰动规律。
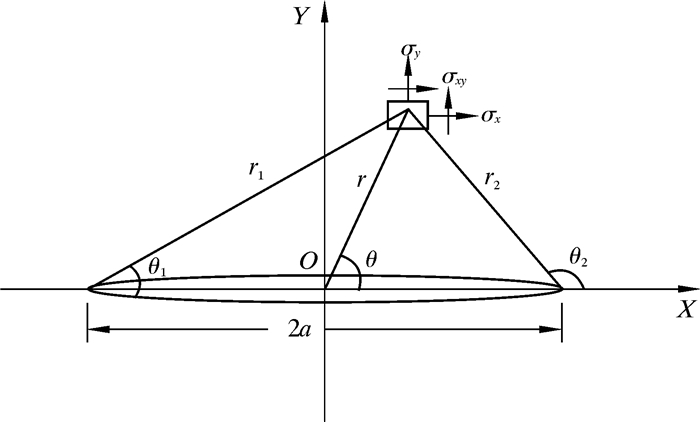
图 1为水力裂缝周围应力在极坐标下示意图。图中:r为裂缝周围任一点到裂缝中心O的距离,m;r1和r2分别是缝周围任一点到裂缝两个端部的距离,m;θ为r与裂缝长轴的夹角,(°);θ1和θ2分别是r1和r2与裂缝长轴的夹角,(°);σr和σθ分别是极坐标下沿r方向和θ方向的主应力,MPa;σrθ是剪应力,MPa。规定拉应力为正,压应力为负。
|
| 图 1 极坐标下裂缝周围应力分量示意图 Fig.1 Schematic diagram of the stress components around the fracture under polar coordinates |
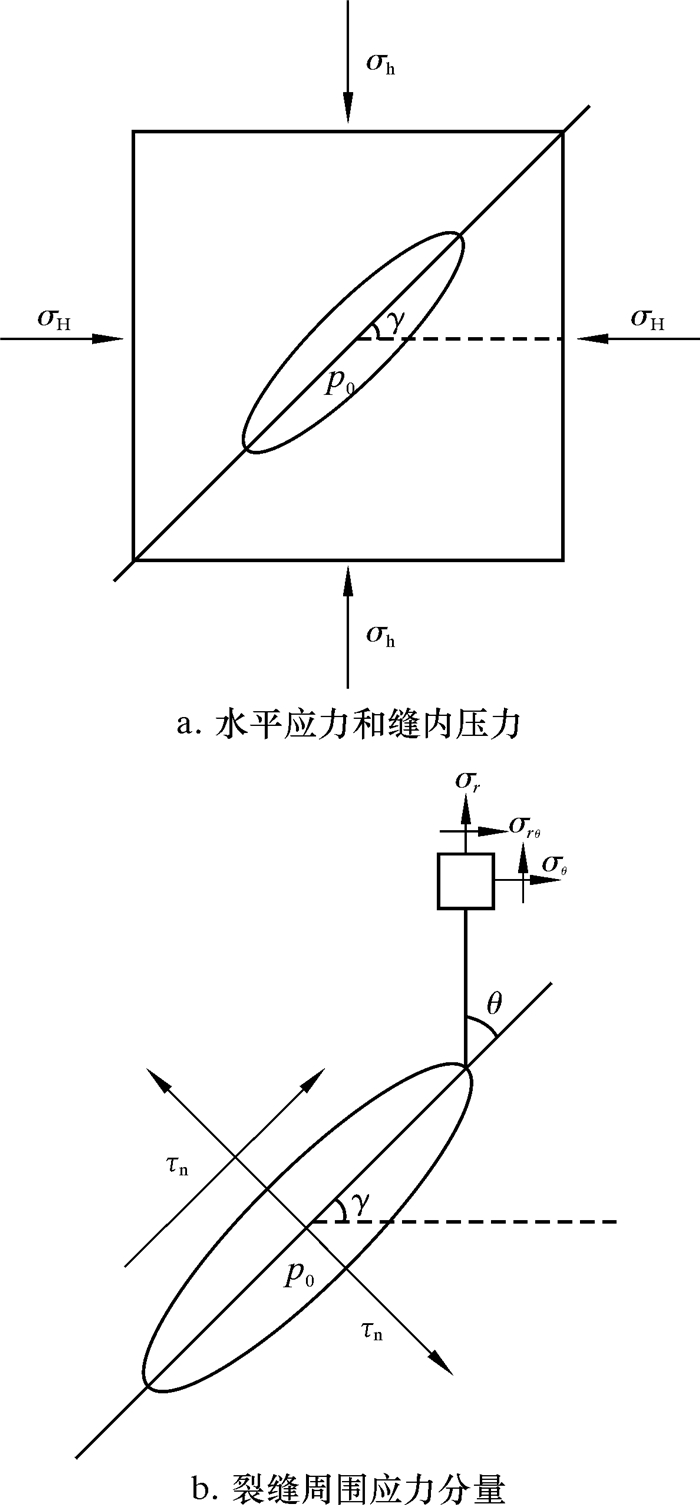
在水平井分段压裂过程中,水平井往往要沿最小水平主应力方向,形成的水力裂缝沿最大水平主应力方向。但是受到钻井经验、设备以及复杂的地质条件限制,井眼轨迹不能完全地沿垂直于最大水平主应力方向延伸,在裂缝和最大水平主应力之间存在一定的夹角γ,如图 2所示。
|
| 图 2 倾斜裂缝受力示意图 Fig.2 Inclined fracture stress diagram |
对于任意裂缝,根据任意斜面上应力分量变化关系,可知作用于裂缝面上的正应力和剪应力表达式分别为:
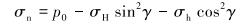
|
(1) |
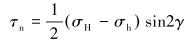
|
(2) |
式中:σn、τn分别是作用在倾斜裂缝表面上的正应力和剪应力,MPa;p0为缝内流体压力,MPa;σH、σh分别是水平最大主应力和水平最小主应力,MPa。
假设地层为线弹性,根据线弹性力学,当裂缝受到拉伸和剪切应力时,裂缝面上的Ⅰ型和Ⅱ型Westergaard应力函数表达式为:
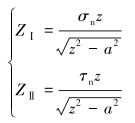
|
(3) |
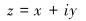
|
(4) |
式中:ZⅠ、ZⅡ分别是Ⅰ型和Ⅱ型应力函数;z是复变函数;a为裂缝半缝长,m。
水力裂缝内部的净压力会产生诱导应力,改变裂缝周围岩体的应力状态。诱导应力分布于裂缝周围,在X-Y二维平面上有σx、σy和τxy3个应力分量。根据叠加准则,当裂缝受到拉剪应力作用时,会产生Ⅰ型和Ⅱ型断裂强度因子,裂缝受到拉剪应力时的诱导应力分量表达式为:
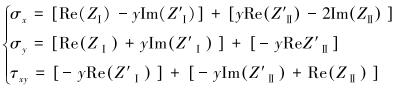
|
(5) |
式中:Z′表示dZ/dz,Re和Im分别表示复变函数的实部和虚部。
Mises屈服准则是工程上应用比较广泛的应力分布计算方法,将式(5)得到的裂缝的应力分量带入Mises应力表达式,得到裂缝周围的应力分布为:
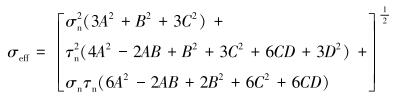
|
(6) |
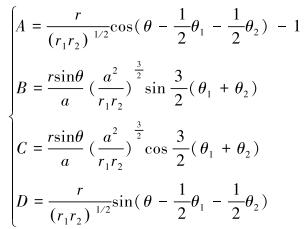
|
(7) |
根据式(6)和式(7)可以计算得到水力裂缝周围的应力分布。
2 复合水力裂缝应力场形态研究选取射孔方向和最大水平主应力夹角α为0°、30°、45°和60°等4种倾斜裂缝,最大水平主应力σH=60 MPa,最小水平主应力σh=40 MPa,缝内流体压力p0=50 MPa。根据式(5)可以计算诱导应力的分量。由于地层非均质性等因素,裂缝在地层中的延伸方向会发生改变,形态会非常复杂,所以为了研究诱导应力的扰动范围,选择在裂缝中心处(井筒处)分析诱导应力的变化情况。
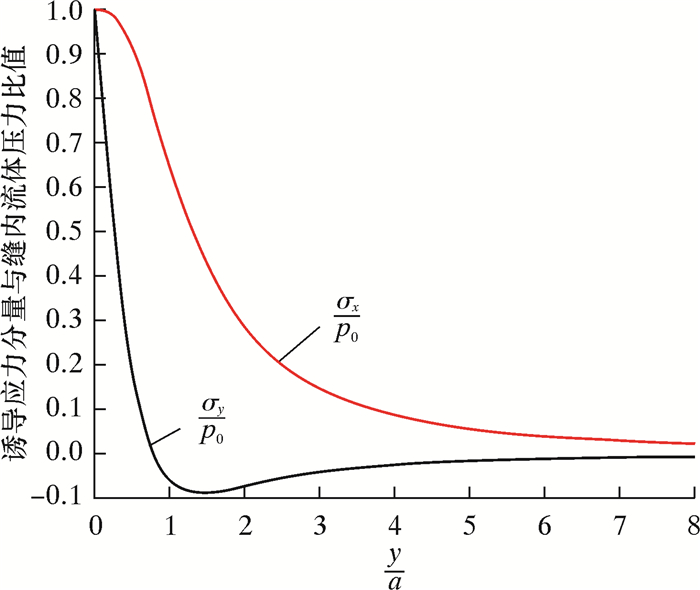
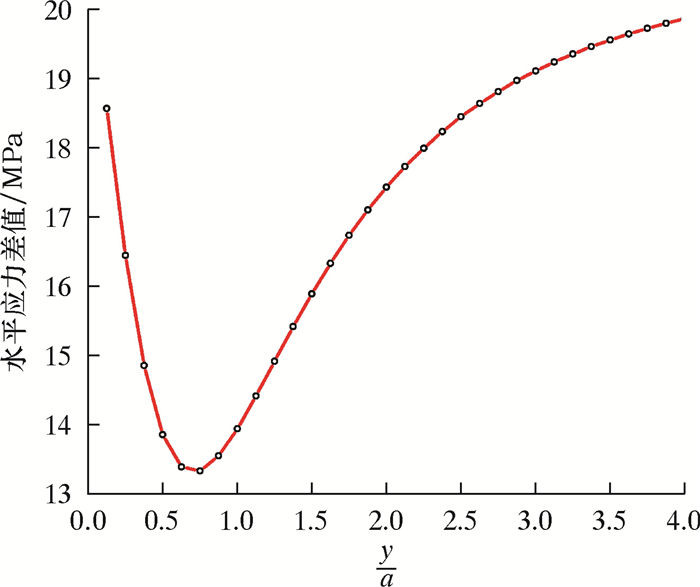
结果发现,随着垂直于裂纹面方向距离的增大,诱导应力分量σx和σy均逐渐减小,并且σx比σy小,如图 3所示。将水力裂缝形成的诱导应力和初始地应力进行叠加,比较沿裂纹面方向和垂直于裂纹面方向的叠加应力差值,发现在垂直于裂纹面方向,超过4倍半缝长时,计算条件下的水平主应力差接近20 MPa(见图 4),和初始的地应力差值基本相等,可以认为诱导应力的扰动作用在超过4倍缝长之后可以忽略不计(相对于给定的水平主应力值σH=60 MPa和σh=40 MPa)。考虑到实际的地应力一般为20~30 MPa(根据地应力梯度可以算出来),笔者选用1 MPa作为标准,判断应力的扰动范围。当应力小于1 MPa时,就认为扰动效应不存在了,在实际的油田地应力中,这个值可能会更小。
|
| 图 3 裂缝诱导应力随垂直于裂纹面方向变化趋势 Fig.3 Trends of fracture induced stress with direction perpendicular to the fracture surface |
|
| 图 4 水力裂缝周围岩体主应力差随垂直于裂纹面方向变化趋势 Fig.4 The main stress difference of rock mass around the hydraulic fracture changes with the direction perpendicular to the fracture surface |
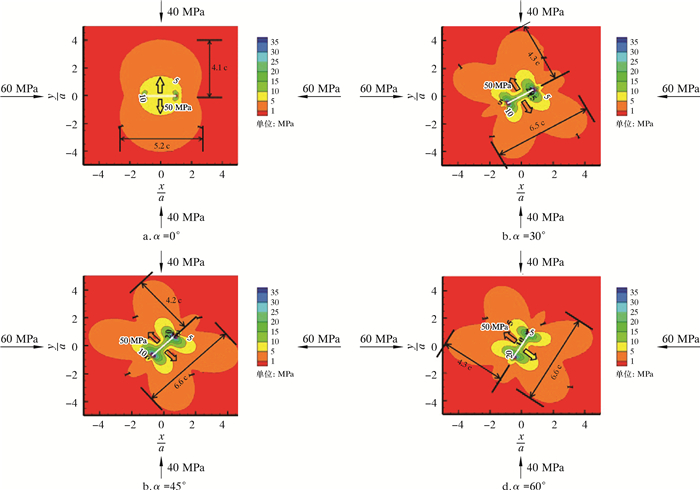
图 5为水力裂缝周围应力分布云图,白线代表裂缝。通过研究发现,当垂直于裂纹面方向距离超过4倍的半缝长时,水力裂缝所产生的诱导应力几乎可以忽略不计。图中橙色区域表示诱导应力扰动区,垂直于裂纹面方向4.1~4.2倍半缝长时,裂缝周围的有效诱导应力为1 MPa,夹角为0°裂缝周围诱导应力扰动区域呈现上下向外凸出的形态,倾斜裂缝周围应力场呈沿裂纹面方向对称分布的“蝴蝶状”。诱导应力干扰区在垂直于裂纹面方向上总的范围是8.2~8.4倍半缝长,沿裂纹面方向总范围是5.2倍半缝长,前者比后者高57.7%~61.5%。
|
| 图 5 射孔方向和最大主应力夹角α不同时水力裂缝Mises应力云图 Fig.5 Mises stress distribution of hydraulic fracture with different angles α between the perforation direction and the maximum principal stress |
3 复合水力裂缝应力场分布机理研究
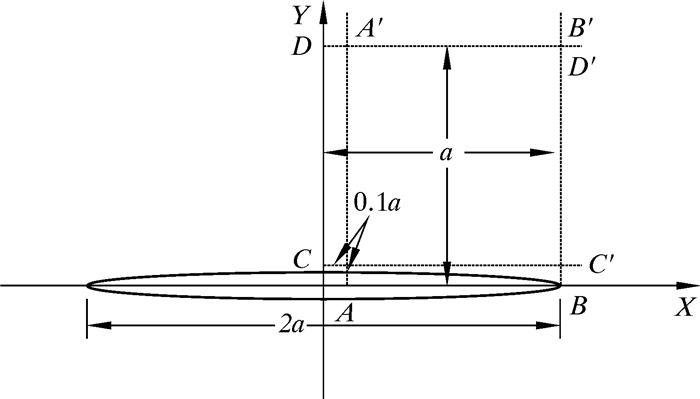
沿裂纹面和垂直于裂纹面方向距离裂缝中心0.1倍半缝长和1个半缝长处各取一条直线(见图 6),研究这些直线上的诱导应力随垂直于裂纹面方向以及沿裂纹面方向的变化规律,结果见图 7~图 10。
|
| 图 6 选取的4条直线示意图 Fig.6 The selected four straight lines |
|
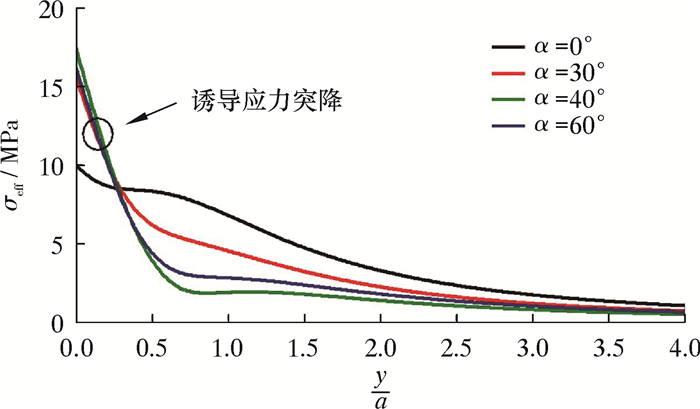
| 图 7 水力裂缝沿直线A-A′的诱导应力变化趋势 Fig.7 Trends of induced stresses of hydraulic fracture along line A-A′ |
|
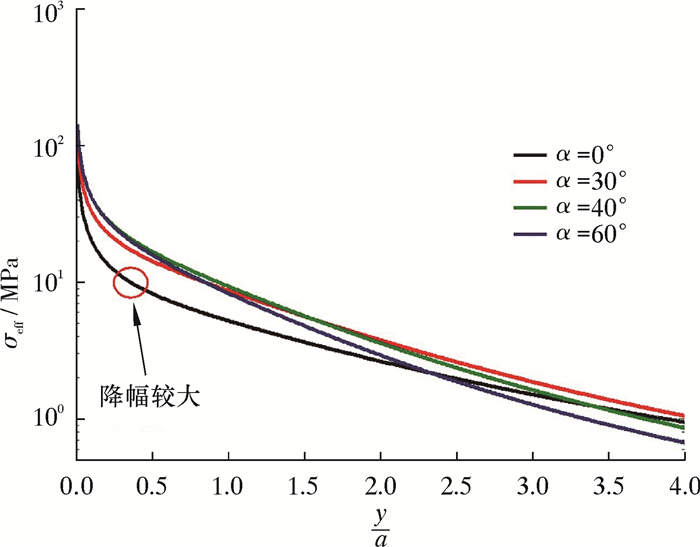
| 图 8 水力裂缝沿直线B-B′的诱导应力变化趋势 Fig.8 Trends of induced stresses of hydraulic fracture along line B-B′ |
|
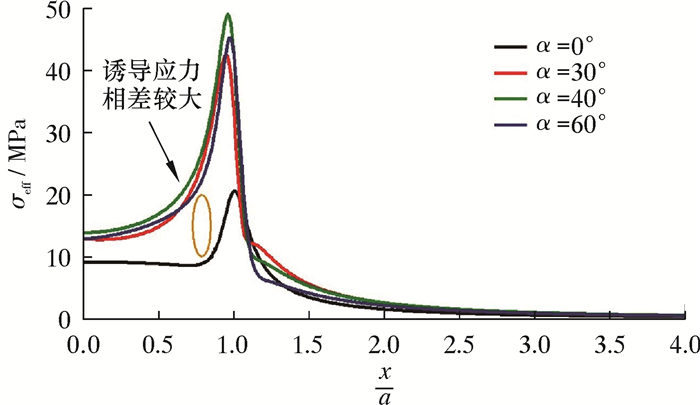
| 图 9 水力裂缝沿直线C-C′的诱导应力变化趋势 Fig.9 Trends of induced stresses of hydraulic fracture along line C-C′ |
|
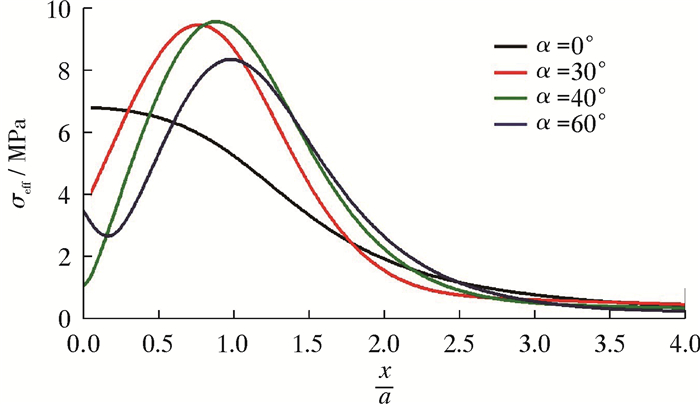
| 图 10 水力裂缝沿直线D-D′的诱导应力变化趋势 Fig.10 Trends of induced stresses of hydraulic fracture along line D-D′ |
图 6为选取的4条直线示意图,X方向为沿裂纹面方向,Y方向为垂直于裂纹面方向。取的4条直线分别为A-A′、B-B′、C-C′、D-D′。A-A′和C-C′距离X轴和Y轴是0.1a,B-B′和D-D′距离X轴和Y轴为半缝长。
图 7和图 8分别为水力裂缝的诱导应力沿直线A-A′和B-B′的变化趋势图,图中纵坐标表示诱导应力值,横坐标表示裂缝沿垂直于裂纹面方向的距离和半缝长a的比值。由图 7可知,诱导应力随垂直于裂纹面方向的距离增大而逐渐减小,倾斜裂缝的诱导应力比夹角为0°裂缝高,但下降的速率较快。沿垂直于裂纹面方向距离达到0.259倍半缝长时,诱导应力均相等。从图 5可知,当诱导应力为1 MPa时,应力扰动基本上没有影响了。因此在图 7和图 8中,在裂缝中心附近,垂直于裂纹面方向的应力扰动范围是2.5~4.1倍半缝长;而在裂缝端部附近,垂直于裂纹面方向的应力扰动范围是3.4~4.2倍半缝长。
图 9和图 10分别为水力裂缝诱导应力沿直线C-C′和D-D′的变化趋势图。由图 9可知,裂缝中心应力沿裂纹面方向逐渐增大,在裂缝端部达到最大值,夹角为0的裂缝应力比倾斜裂缝小5~30 MPa,诱导应力随裂缝方向距离的增大而增大,当距离达到半缝长时,诱导应力达到最大值,随后逐渐减小。由图 10可知,倾斜裂缝应力沿裂纹面方向逐渐增大,在缝端达到最大值,夹角为0°裂缝应力沿裂纹面方向逐渐减小。沿裂纹面方向的应力扰动范围为2.2~2.6倍半缝长。
根据上面的分析,得到夹角为0°裂缝和倾斜裂缝的裂缝中心区域和缝端区域的应力扰动范围,如表 1所示。
| 应力扰动方向 | 水平裂缝应力扰动范围 | 倾斜裂缝应力扰动范围 |
| 垂直于裂纹面中心区域直线A-A’ | 4.1a | 2.5a~3.2a |
| 垂直于裂纹面缝端直线B-B’ | 3.7a~3.8a | 3.4a~4.2a |
| 裂纹附近沿裂纹面方向直线C-C’ | 2.2a | 2.4a~2.6a |
| 裂纹远端沿裂纹面方向直线D-D’ | 2.3a~2.6a | 2.2a~2.6a |
在流体压力和地应力的双重作用下,倾斜裂缝面上受到拉剪应力,由于剪应力沿着裂缝面向端部滑移,造成了裂缝中心区域的应力相应减小,而应力在裂缝端部发生集中,而夹角为0°裂缝缝面不存在剪应力,应力不会向缝两端滑移,这是造成其应力场和倾斜裂缝应力场形态和分布不同的主要原因,所以倾斜裂缝的应力场呈“蝴蝶状”形态,夹角为0°裂缝的应力场呈现向外凸出的形态。
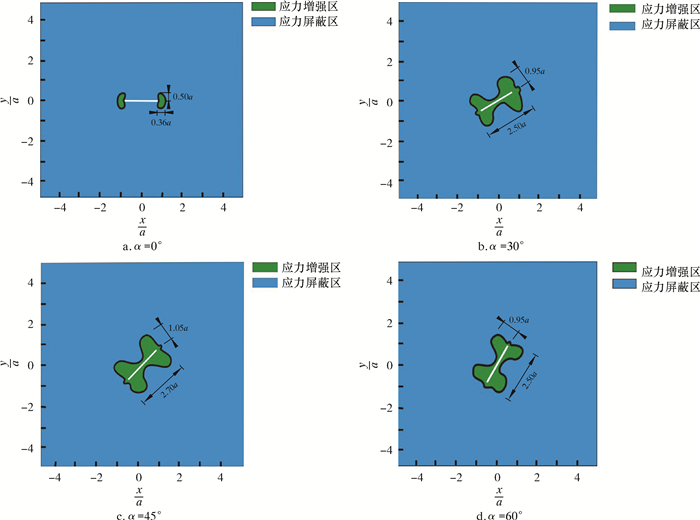
应力增强区表示应力比缝内原始净压力值大,应力屏蔽区表示应力比缝内原始净压力小。由图 5的计算结果可知,裂缝周边的应力存在大于缝内原始净压力(10 MPa)的区域,说明存在应力增强区,相应的必然存在应力屏蔽区。倾角为0°、30°、45°和60°裂缝的应力增强区和应力屏蔽区如图 11所示。
|
| 图 11 水力裂缝应力扰动增强区域和屏蔽区域 Fig.11 The enhancement area and shielding area of hydraulic fracture stress disturbance |
从图 11可以看出,当裂缝和最大水平主应力平行时,应力增强区只存在于裂缝尖端,范围为沿裂纹面方向0.36倍半缝长,垂直于裂纹面方向1.0倍半缝长;当裂缝和最大水平主应力存在倾角时,裂缝的应力增强区为沿裂纹面对称的“蝴蝶状”区域,范围为沿裂纹面方向2.5倍半缝长,垂直于裂纹面方向1.9~2.1倍半缝长。这说明当裂缝不平行于最大水平主应力方向延伸时,形成的诱导应力比沿最大水平主应力方向延伸的裂缝高,作用的范围广。
4 结论建立了倾斜水力裂缝周围应力模型,在地应力条件下,通过计算4组不同倾角的水力裂缝周围应力分布,得到以下结论:
(1) 平行于最大水平主应力的裂缝的应力扰动区呈现向外凸出的形态,不平行于最大水平主应力的裂缝的应力扰动区呈现“蝴蝶状”,且所有的扰动区均沿裂纹面方向对称分布。
(2) 在裂缝周围存在应力增强区和应力屏蔽区,它们的范围随裂缝的倾斜角变化而变化。当裂缝不平行于最大水平主应力方向延伸时,形成的诱导应力比沿最大水平主应力方向延伸的裂缝高,作用的范围广。
(3) 裂缝的诱导应力随射孔方向和最大水平主应力夹角而变化。垂直于裂纹面方向的应力扰动范围比沿裂纹面方向的应力扰动范围高57.7%~61.5%,平行于最大水平主应力方向的裂缝中心区域垂直于裂纹面的应力诱导范围比端部高7.9%~10.8%,不平行于最大水平主应力方向的裂缝中心区域垂直于裂纹面应力诱导范围比端部低23.8%~26.4%。沿裂纹面方向,两者的应力扰动范围相差不大。
(4) 在水平井分段压裂过程中,通过对射孔方向和最大水平主应力夹角的分析,可以避开相邻裂缝的诱导应力干扰,达到稳定增产的目的。
| [1] | ZHOU J, CHEN M, JIN Y, et al. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(7): 1143-1152. DOI: 10.1016/j.ijrmms.2008.01.001 |
| [2] | ROUSSEL N P, SHARMA M M. Strategies to minimize frac spacing and stimulate natural fractures in horizontal completions[R]. SPE 146104, Denver, Colorado, USA: SPE, 2011. http://www.researchgate.net/publication/238050155_Strateg |
| [3] | ROUSSEL N P, SHARMA M M. Quantifying transient effects in altered-stress refracturing of vertical wells[R]. SPE 119522, The Woodlands, Texas: SPE, 2009. https://www.researchgate.net/publication/245418535_Quantifying_Transient_Effects_in_Altered-Stress_Refracturing_of_Vertical_Wells |
| [4] | SNEDDON I N. The distribution of stress in the neighbourhood of a crack in an elastic solid[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1946, 187(1009): 229-260. DOI: 10.1098/rspa.1946.0077 |
| [5] | ROUSSEL N P, SHARMA M M. Optimizing fracture spacing and sequencing in horizontal well fracturing[R]. SPE 127986, Lafayette, Louisiana, USA: SPE, 2010. http://www.researchgate.net/publication/254552452_optimizing_fracture_spacing_and_sequencing_in_horizontal-well_fracturing |
| [6] | 邓华锋, 李建林, 刘杰, 等. 考虑裂隙水压力的岩体压剪裂纹扩展规律研究[J]. 岩土力学, 2011, 32(增刊1): 297-302. DENG H F, LI J L, LIU J, et al. Research on propagation of compression shear fracture in rocks considering fissure water pressure[J]. Rock and Soil Mechanics, 2011, 32(S1): 297-302. |
| [7] | 汤连生, 张鹏程, 王洋. 水作用下岩体断裂强度探讨[J]. 岩石力学与工程学报, 2004, 23(19): 3337-3341. TANG L S, ZHANG P C, WANG Y, et al. On fracture strength of rocks with cracks under water pressure and chemical damage[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3337-3341. DOI: 10.3321/j.issn:1000-6915.2004.19.021 |
| [8] | 王元汉, 徐钺, 谭国焕, 等. 岩体断裂的破坏机理与计算模拟[J]. 岩石力学与工程学报, 2000, 19(4): 449-452. WANG Y H, XU Y, TAN G H, et al. Fracture mechanism and calculation of rock fracture[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(4): 449-452. |
| [9] | 胡强法, 朱峰, 李宪文, 等. 水力喷砂射孔与起裂大型物理模拟试验[J]. 中国石油大学学报(自然科学版), 2011, 35(6): 81-87. HU Q F, ZHU F, LI X W, et al. Physical simulating experiments of hydrajet perforating and fracture initiation process[J]. Journal of China University of Petroleum, 2011, 35(6): 81-87. |
| [10] | 姜浒, 陈勉, 张广清, 等. 定向射孔对水力裂缝起裂与延伸的影响[J]. 岩石力学与工程学报, 2009, 28(7): 1321-1326. JIANG H, CHEN M, ZHANG G Q, et al. Impact of oriented perforation on hydraulic fracture initiation and propagation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1321-1326. |
| [11] | 张广清, 陈勉. 定向射孔水力压裂复杂裂缝形态[J]. 石油勘探与开发, 2009, 36(1): 103-107. ZHANG G Q, CHEN M. Complex fracture shapes in hydraulic fracturing with orientated perforations[J]. Petroleum Exploration and Development, 2009, 36(1): 103-107. |



