0 引言
作为压裂作用中的主要流动通道,高压管汇扮演着举足轻重的角色。在水力压裂过程中,高压管汇原件承受着固液两相流的冲蚀磨损作用。在长期的使用过程中,压裂液以及支撑剂颗粒的冲蚀破坏造成的凹坑会引发高压管汇的破裂甚至穿孔,因此对于不同几何形状和尺寸的高压管汇失效分析尤为重要。
针对水力压裂工况,目前对高压管汇的冲蚀失效研究分析还很少。张继信等[1-2]针对典型的弯管冲蚀磨损进行了数值模拟,研究了不同连接结构下高压管汇的冲蚀分布规律,并建立了固液两相流的数学模型,分析了支撑剂的质量浓度、密度、动力黏度以及携砂流量对于高压管汇的冲蚀影响规律,指出了对管壁影响最严重的因素;周兆明等[3]基于计算动力学软件FLUENT建立了离散相数学模型,计算出了岩屑粒子对高压管汇的冲蚀量和离散相分布量;M.SUZUKI等[4]研究了不同直径颗粒对高压管汇内壁的碰撞以及相关的近壁面函数的设置分析,但是忽略了高压管汇内壁直径、弯曲度以及弯管段曲率半径对高压管汇冲蚀磨损率影响的研究。
笔者以高压管汇作为研究分析对象,通过建立离散相模型,研究压裂液对高压管汇的冲蚀分布规律,分析不同管道直径、不同管道弯曲度以及不同的弯管曲率半径在不同的流速下压裂液对高压管汇的冲蚀磨损规律,以期为高压管汇的失效、预防以及安全防护提供参考依据。
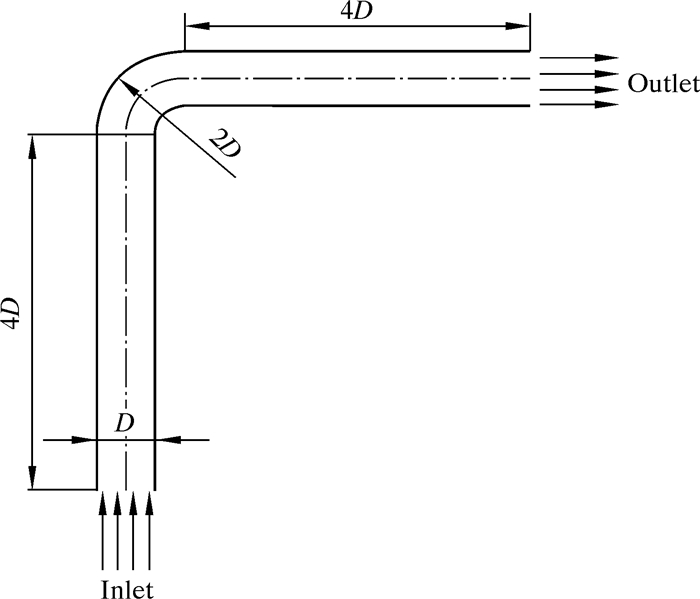
1 高压管汇数值模拟 1.1 几何模型笔者通过建立高压管汇冲蚀几何模型进行数值仿真来实现对高压管汇内壁冲蚀磨损的研究。以弯曲度为90°的高压管汇为研究对象,建立高压管汇模型的内径为45 mm,弯管段曲率半径为90 mm,直管段长度为225 mm,网格划分采用六面体网格。高压管汇几何模型如图 1所示。
|
| 图 1 高压管汇几何模型 Fig.1 The geometry model of the high-pressure manifold |
1.2 控制方程
高压管汇的模型分为直管段和弯管段,为了保证计算的精确度而不至于失真,选用RNG k-ε湍流模型对高压管汇的冲蚀磨损规律进行研究。控制方程为:
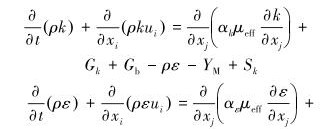
|
(1) |
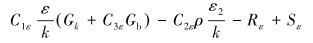
|
(2) |
式中:t为时间,s;ρ为连续相的密度,kg/m3;k为湍流动能,J;ε为湍流耗散率,J/s;xi、xj为位移,m;i、j=1、2、3,分别代表x、y、z坐标系,i≠j;ui为速度,m/s; αk为k方程的普朗特数,J;αε为ε方程的普朗特数,J;YM为湍流中过度扩散产生的波动,J;Sk、Sε为自定义参量,C1、C2、C3为经验常数,Rε为ε的函数。
1.3 冲蚀磨损模型可将Finner冲蚀磨损理论计算公式[2]应用到高压管汇冲蚀磨损机理研究中。N个支撑剂颗粒对高压管汇内壁的冲蚀磨损速率计算式为:
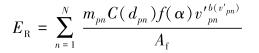
|
(2) |
式中:ER为冲蚀速率,kg/(m3·s);mpn为颗粒质量流量,kg/s;C(dp)为颗粒粒径函数;f(α)为冲蚀攻角函数;N为发生碰撞的颗粒数量;v′p为颗粒相对于管壁的碰撞速度,m/s;b(vp)为颗粒速度相关函数;Af为高压管汇冲蚀计算单元面积,m2。
1.4 边界条件设定综合考虑到水力压裂工况,利用流体动力学分析软件FLUENT离散相模型来模拟高压管汇内部的固液两相流流动[5]。液相作为连续相,颗粒作为离散相。在计算高压管汇的冲蚀磨损时,冲蚀介质为清水加砂,离散相为支撑剂颗粒。由于携砂液流量或进口速度对于管汇冲蚀的冲蚀磨损影响极大,设定在管汇进口处的携砂液流量为1.59 m3/min,支撑剂质量浓度为18 kg/m3,支撑剂颗粒粒径为0.001 m,视密度为3 000 kg/m3,体积密度为1 800 kg/m3,砂比为1%~14%(离散相取0.3%~7.0%),流体动力黏度为0.001 Pa·s。
高压管汇进口设置为速度进口边界,并且在进口处压裂液和离散相颗粒的速度大小相同,出口设置为自由流出。壁面处采用标准壁面函数处理,颗粒粒径采用均匀分布,选用随机追踪模型预测颗粒的弥散,压力速度耦合采用SIMPLE算法,动量、能量、湍动能和湍流耗散率的离散均采用二阶迎风格式,设定壁面边界为反射边界,反弹系数及冲蚀参数参照A.FORDER[6]和K.AHLERT等[7]的研究成果取值。
2 高压管汇冲蚀磨损结果与分析通过FLUENT软件数值模拟计算,得出了高压管汇的冲蚀磨损分布规律,其冲蚀磨损率和离散量分布分别如图 2和图 3所示。
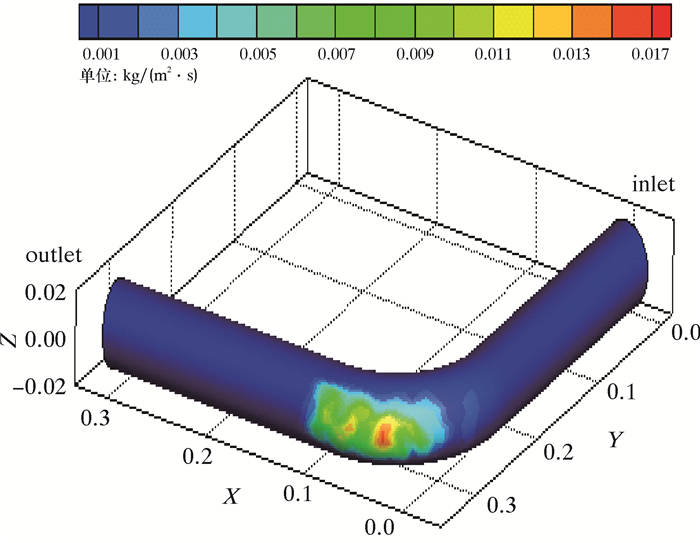
|
| 图 2 高压管汇冲蚀磨损率分布 Fig.2 The erosion wear rate distribution of the high-pressure manifold |
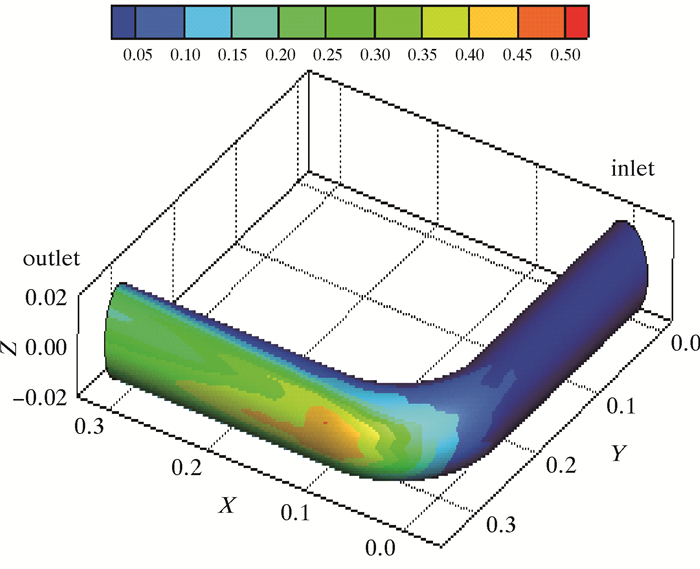
|
| 图 3 高压管汇冲蚀离散量分布 Fig.3 The erosion wear dispersion distribution of the high-pressure manifold |
从图 2和图 3可知,在高压管汇遭受冲蚀的过程中,在高压管汇进、出口的直管段几乎没有发生冲蚀磨损,发生冲蚀磨损最严重的部位集中在弯管部分,并且在弯管的出口处冲蚀磨损最严重,冲蚀率达到0.017 6 kg/(m2·s);颗粒离散量分布在高压管汇的进口直管段处十分微小,离散量分布密集区域主要集中在弯管出口处到直管的出口段,且从弯管出口处到直管的出口段离散量分布逐渐减少。
由于高压管汇的几何尺寸不一,所以研究在不同的流速和不同几何尺寸高压管汇的离散相冲蚀磨损率的变化情况也极为重要。几何尺寸主要包括高压管汇内壁直径、弯管的曲率半径以及弯管段的弯曲度3类参数。
2.1 内壁直径对冲蚀结果的影响在进行计算流体动力学软件模拟仿真时,取高压管汇的内壁直径范围为30~150 mm,分别设定进口流速v为5、10、15、20和25 m/s,计算得到在不同的高压管汇内壁直径下弯管的最大冲蚀磨损率和平均冲蚀磨损率变化情况,如图 4所示。
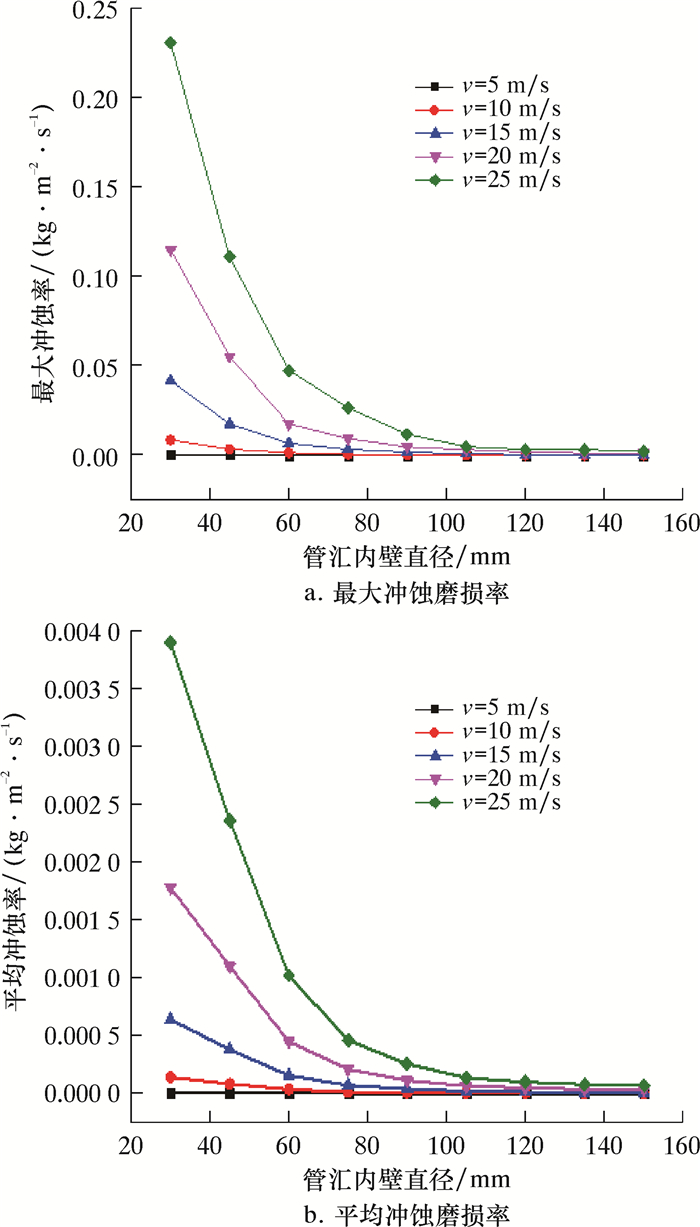
|
| 图 4 管汇内壁直径对管汇冲蚀磨损率的影响 Fig.4 Effect of the manifold inner diameter on the manifold erosion wear rate |
从图 4可知,在进口流速一定的情况下,随着管汇内壁直径的增大,管汇内壁的最大冲蚀磨损率和平均冲蚀磨损率呈现递减的趋势,并且随着进口流速的增加,管汇内壁的最大冲蚀磨损率和平均磨损率逐渐增大。管汇内壁直径在30~150 mm的范围内,分别在5、10、15、20和25 m/s的进口流速下,最大冲蚀磨损率减小了98.61%、98.72%、98.70%、98.80%和98.96%,平均冲蚀磨损率减小了95.51%、98.78%、98.71%、98.11%和98.04%,在不同的速度下管汇最大冲蚀磨损率最大达到了0.230 kg/(m2·s)。其原因在于,管汇内壁直径增大,使得支撑剂颗粒与管汇内壁的碰撞面积增大,在管内压裂液的冲蚀下,单位面积上受到离散相颗粒冲蚀作用的数量减少,导致冲蚀磨损率减小。而冲蚀速度的加快,单位面积上所受到颗粒的冲蚀动能成倍数增加,加重了管道内壁的冲蚀磨损。
2.2 弯管段的曲率半径对冲蚀结果的影响在进行FLUENT数值模拟时,取高压管汇弯管段的曲率半径范围为90~360 mm,分别设定进口流速v为5、10、15、20和25 m/s,计算得到在不同高压管汇弯管段曲率半径下的弯管最大冲蚀磨损率和平均冲蚀磨损率变化情况,如图 5所示。
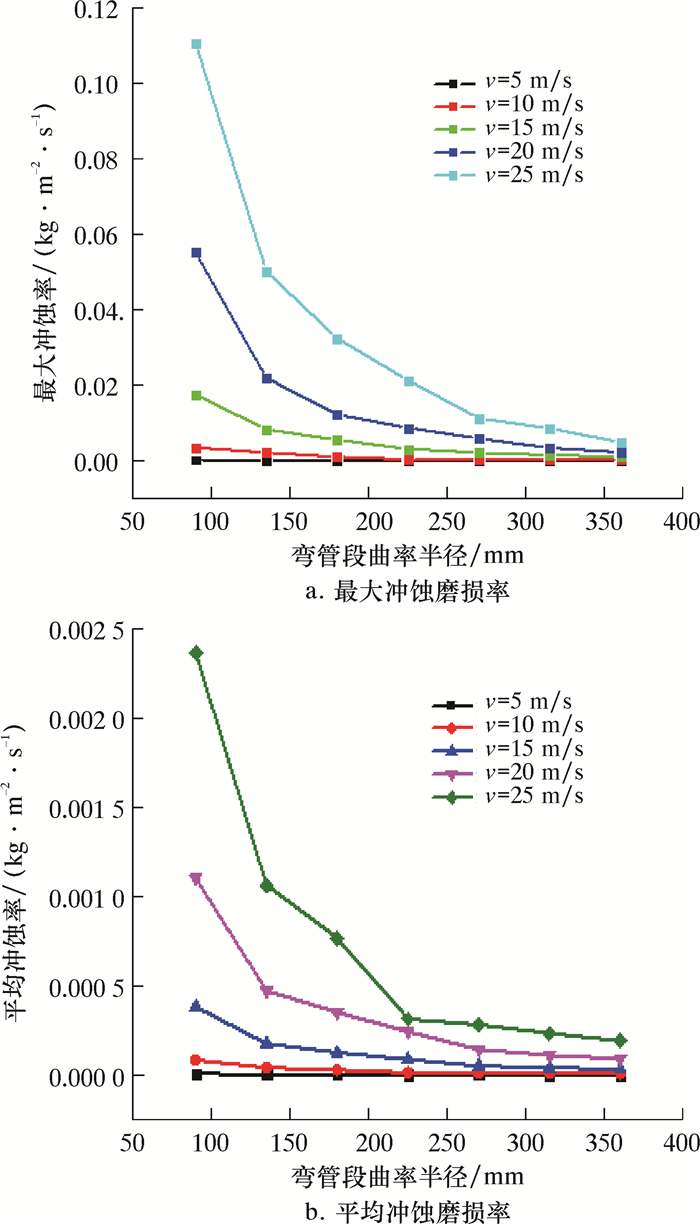
|
| 图 5 管汇弯管段曲率半径对管汇冲蚀磨损率的影响 Fig.5 Effect of the curvature radius of bend on the manifold erosion wear rate |
从图 5可知,随着管汇弯管段曲率半径的增加,管汇的最大冲蚀率和平均冲蚀率不断减小,但减小的幅度也逐渐减小,并且随着进口流动速度的增大,管汇的最大冲蚀率和平均冲蚀率逐渐增大。在曲率半径90~360 mm的范围内,在速度5、10、15、20和25 m/s时,管汇最大冲蚀率分别增加了21.0、11.0、14.7、22.7和21.4倍,平均冲蚀率分别增加了10.6、10.8、11.0、11.3和11.4倍,在不同的速度下管汇最大冲蚀磨损率达到了0.110 kg/(m2·s)。其原因在于,弯管段曲率半径增大,弯管的弯曲程度越小,对于内壁的离心力减小,支撑剂颗粒对于内壁的冲击力也会随之减小,则单位面积上冲蚀磨损率减小,而流动速度的增大也加剧了管汇的冲蚀。
2.3 弯管段的弯曲度对冲蚀结果的影响高压管汇弯管段的弯曲度是指进口直管段与出口直管段的角度。在进行流体数值模拟时,取高压管汇弯管段弯曲度的角度范围为45°~150°,分别设定进口流速v为5、10、15、20和25 m/s,计算得到在不同高压管汇弯管段的弯曲度下弯管的最大冲蚀磨损率和平均冲蚀磨损率变化情况,如图 6所示。
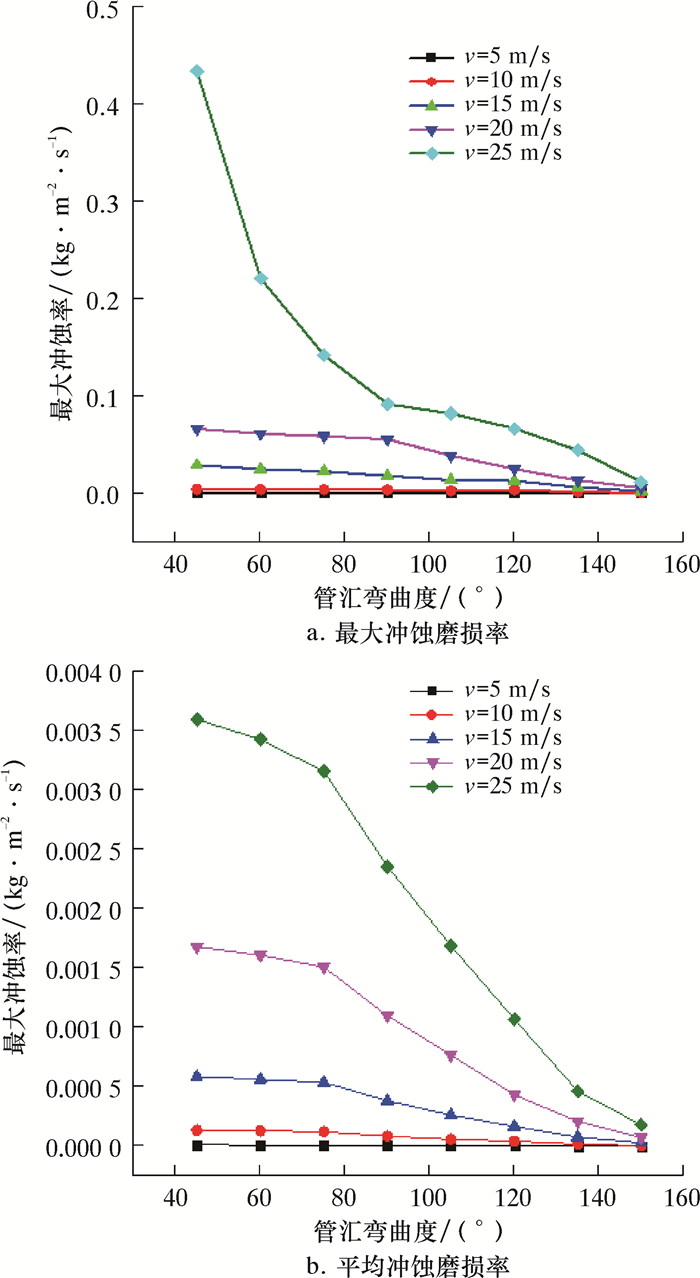
|
| 图 6 管汇弯曲度对管汇冲蚀磨损率的影响 Fig.6 Effect of bend curvature on manifold erosion wear rate |
从图 6可知,随着管汇弯管段弯曲度的增大,管汇内壁的最大冲蚀磨损率和平均冲蚀磨损率逐渐减小,并且随着进口流动速度的增大,管汇的最大冲蚀率和平均冲蚀率逐渐增大。在速度为5、10、15、20和25 m/s时,管汇的最大冲蚀磨损率和平均冲蚀磨损率在45°~150°的弯曲度范围内,分别减小了85.71%、85.29%、92.31%、90.91%,97.30%和95.00%、95.00%、95.00%、95.23%,94.74%,在不同的速度下管汇最大冲蚀磨损率最大达到了0.434 kg/(m2·s)。其原因在于,管汇弯曲度的增加,离散相颗粒的运动方向发生变化,对弯管段内壁的冲击碰撞次数减小,且冲击碰撞内壁的离散相颗粒的数量也会随之减小,从而对管汇的冲蚀率减小。
通过对比,不难发现对管汇冲蚀磨损影响最严重的因素是弯管段的弯曲度,而冲蚀磨损率增长最快的影响因素是管汇内壁直径。
3 结论(1) 高压管汇的弯管出口处发生冲蚀磨损最严重,离散量集中分布在弯管处至直管出口处,而在直管段冲蚀磨损率很小,并且管汇的内壁直径、弯管段的弯曲度以及弯管曲率半径对管汇的冲蚀磨损有很大的影响。
(2) 随着管汇的内壁直径、弯管曲率半径和弯管段的弯曲度3种因素的增大,管汇的最大冲蚀磨损率和平均冲蚀磨损率减小,而随着进口流速的增加,管汇的最大冲蚀磨损率和平均冲蚀磨损率增大,最大的冲蚀磨损率分别是0.230、0.110和0.434 kg/(m2·s)。
(3) 可根据工况的实际需求,通过改变进口流速或者携砂量,合理地选择管汇参数以减小管汇的冲蚀磨损。
| [1] | 张继信, 康健, 樊建春, 等. 高压弯管冲蚀失效分析及数值模拟[J]. 润滑与密封, 2016, 41(10): 40-46. ZHANG J X, KANG J, FAN J C, et al. Failure analysis and numerical simulation of high pressure elbow erosion wear[J]. Lubrication Engineering, 2016, 41(10): 40-46. DOI: 10.3969/j.issn.0254-0150.2016.10.008 |
| [2] | 张继信, 樊建春, 汪彤, 等. 压裂液对高压弯管冲蚀作用的数值分析[J]. 润滑与密封, 2013, 38(4): 27-31. ZHANG J X, FAN J C, WANG T, et al. Research on erosion wear of fracturing fluid on high pressure elbow[J]. Lubrication Engineering, 2013, 38(4): 27-31. |
| [3] | 周兆明, 练章华, 万夫. 高压管汇冲蚀磨损的多相流仿真[J]. 计算机辅助工程, 2013, 22(5): 101-104. ZHOU Z M, LIAN Z H, WAN F. Multiphase flow simulation on erosion of high-pressure manifold[J]. Computer Aided Engineering, 2013, 22(5): 101-104. |
| [4] | SUZUKI M, INABA K, YAMAMOTO M. Numerical simulation of sand erosion in a square-section 90-degree bend[J]. Journal of Fluid Science and Technology, 2008, 3(7): 868-880. DOI: 10.1299/jfst.3.868 |
| [5] | 任宪忠. 多相混输管道90°弯管冲蚀破坏应力分析[D]. 大庆: 东北石油大学, 2014. REN X Z. Multiphase pipeline 90 degrees elbow erosion stress analysis[D]. Daqing: Northeast Petroleum University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yqcy201106006 |
| [6] | FORDER A, THEW M, HARRISON D. A numerical investigation of solid particle erosion experienced within oilfield control valves[J]. Wear, 1998, 216(1): 184-193. |
| [7] | AHLERT K. Effects of particle impingement angle and surface wetting on solid particle erosion of AISI 1018 steel[D]. Tulsa: The University of Tulsa, 1994. http://www.researchgate.net/publication/313747119_Effects_of_particle_impingement_angle_and_surface_wetting_on_solid_particle_erosion_of_AISI_1018_Steel |




