2. 中石化石油工程设计有限公司
2. Sinopec Petroleum Engineering Corporation
0 引言
导管架平台结构简单、安全可靠、造价低廉且适应性强[1],是5~200 m水深范围内应用最多且行之有效的一种平台形式[2]。随着导管架平台由浅海向深海不断发展,导管架的总体尺寸和质量越来越大,100 m以上水深的导管架质量达到几千吨甚至几万吨,往往超过可使用的浮吊资源能力要求,这时采用导管架滑移下水是目前唯一可行的安装方法。导管架滑移下水过程是指导管架从有一定纵倾的下水驳船上沿滑道靠自重滑动入水,直至与驳船分离并在水中达到漂浮状态的过程。滑移下水是导管架整个安装过程中最重要也是风险最大的环节之一。如果在下水过程中出现失误,将会发生导管架构件局部破坏、下水驳船损毁或导管架与下水驳船一起倾覆等事故,导致工程延期和巨大的经济损失[3]。因此,必须预先对导管架下水过程进行详细计算与论证,设计出最佳下水方案,以充分保障下水工程的安全性与可靠性。
影响导管架下水轨迹与安全性的参数众多,传统的导管架下水设计一般凭借工程经验或工程类比法,通过不断试算来找寻优化方案,带有较大的主观随意性,下水参数的选择也缺乏理论根据和方向性,严重影响设计效率和最终优化方案的可靠性与经济性。因此,有必要详细分析各个参数变化对下水过程的影响规律,为导管架安装设计提供数值依据,使下水参数的优选更加快速准确。
尽管国内外针对海洋导管架滑移下水的理论研究和数值模拟已有30多年,取得了很多的研究成果[3-8],但是关于下水参数对导管架下水的影响规律性研究还很少。为此,笔者以东海某导管架下水设计为工程背景,选取驳船初始吃水、驳船初始纵倾角度、导管架在驳船上的放置位置及滑道滑动摩擦因数等下水参数进行研究,以导管架下水三维时域数值模拟为基础,以导管架入水安全且结构受力最小为优化目标,采用正交试验方法[9],对所得的数值计算结果进行参数敏感性分析,确定出优化的导管架下水设计方案。所得结论可为导管架滑移下水方案的优化设计提供参考。
1 正交试验方案设计 1.1 正交试验法正交试验法是多因素优化中常用的一种高效率试验设计方法。它利用数理统计学与正交性原理[10],从大量的试验点中挑选出部分具有代表性和典型性的试验点,利用正交表科学合理地设计部分试验代替全面试验,大大减少了试验次数。试验中每一因素不同水平的试验次数相同,且与不同因素的各水平相遇的概率相等。通过对部分试验结果分析,能系统了解全面试验的情况,得出各因素对指标的影响程度,并确定因素的主次效应顺序,最终搜索出最优或较优的试验方案,从而达到对试验参数优化的目的。正交试验法兼顾了简单对比法次数少和全面试验法结论可靠的优点,克服了简单对比法试验工况代表性差和全面试验法工作量巨大的缺点,具有均衡分散性和整齐可比性的特点,且试验数据的计算分析较简化。
1.2 试验因素与水平的确定影响导管架下水过程的因素很多,其中有些参数是人为可控的。为此,选取驳船初始吃水、驳船初始纵倾角度、导管架在驳船上的放置位置及滑道滑动摩擦因数等4个可以调节的下水参数,作为正交试验的试验因素。以东海某大型导管架滑移下水工程为研究对象,根据相关规范要求和工程经验确定各因素水平。
驳船舯部初始吃水通常为型深的60%~80%,因此,初始吃水参数每隔0.5 m分别选取7~9 m之间的共5个水平值。初始纵倾角通常在3°~5°之间选取,以克服初始的滑道静摩擦力。本例初始纵倾参数每隔0.5°分别选取3°~5°之间的共5个水平值。导管架在驳船上的位置需要结合连续滑靴布置、导管架拖航分析、下水分析及艏需预留的操作空间等综合因素确定。本例选择导管架距离艏65、70、75、80和85 m(即滑靴压摇臂2、7、12、17及22 m)等5个水平值。不同接触面的滑动摩擦因数有较大不同,如木头和聚四氟乙烯之间的动力摩擦因数为0.03~0.08;木头和涂有润滑剂的钢板之间的动力摩擦因数为0.02~0.12;木头和特氟龙之间的滑动摩擦因数为0.05。本例选择0.03、0.04、0.05、0.06及0.07等5个不同的摩擦因数。试验选定的4个因素及每个因素所对应的各5个水平值见表 1。为了叙述方便,驳船初始吃水、驳船初始纵倾、装船位置和滑动摩擦因数分别用字母A、B、C、D表示。
| 水平 | 试验因素 | |||
| 驳船初始吃水/m | 驳船初始纵倾/(°) | 装船位置/m | 滑动摩擦因数 | |
| 1 | 7.0 | 3.0 | 65 | 0.03 |
| 2 | 7.5 | 3.5 | 70 | 0.04 |
| 3 | 8.0 | 4.0 | 75 | 0.05 |
| 4 | 8.5 | 4.5 | 80 | 0.06 |
| 5 | 9.0 | 5.0 | 85 | 0.07 |
1.3 试验方案设计
根据试验因素个数与水平数,忽略各因素之间的交互作用,按常用正交试验表[10] L25(56)设计了4因素5水平正交试验方案,共25次试验,显然比全面试验(54=625次)的次数大大减少,提高了工作效率。
下水方案的优劣是一个典型的多指标综合评价问题。其中,下水轨迹、导管架最小泥面间隙和下水过程中作用于结构上的各种力及其相互作用力为主要考核指标。研究结果表明[11]:对于不同的下水参数,在数值计算结果满足规范的前提下,其下水轨迹基本一致,只是作用在导管架上的载荷大小以及下水时间长短有差别。导管架距离海底泥面的最小安全距离是导管架下水安全性必须关注的重要指标之一。对于深水大型导管架而言,安装方案设计往往是导管架方案设计的主要控制环节。通过优化设计保证导管架刚度大、结构质量最轻、使平台结构兼具可靠性和经济性是工程前期结构方案的主要工作之一[12]。导管架通过摇臂翻转入水时受到很大的砰击力,容易对导管架下水杆件造成局部破坏。为此,在各下水方案满足规范要求的前提下,以使导管架下水安全且作用在结构上的载荷最小作为下水参数优化的主要目标,选取导管架泥面间隙和对结构强度影响最大的摇臂最大反力以及导管架最大拍击速度等3个指标进行考察。
2 导管架下水数值模拟 2.1 导管架模型导管架采用8腿12裙桩结构,设有6个水平层,主尺度为45.00 m×39.77 m×109.00 m;设计质量为5 612 t,浮力为65.95 MN,总质量为5 749 t,最大排水量为6 744 t;注水杆件在注水前的储备浮力为16.60%,大于15.00%的规范要求;注水后的剩余浮力为6.18%,大于规范的5.00%要求,其中,剩余浮力=(最大浮力-设计重力)/最大浮力×100%。
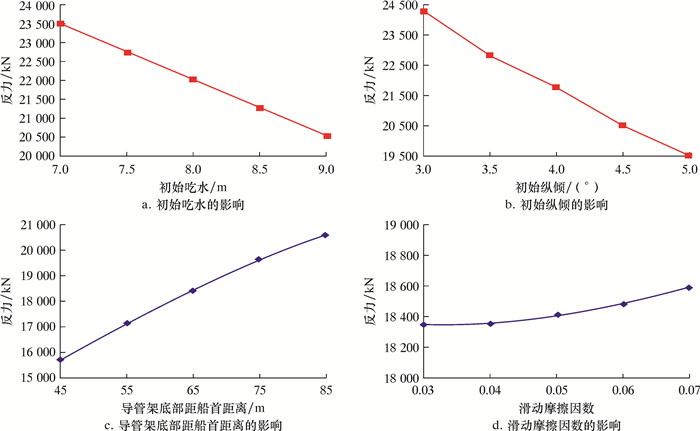
2.2 下水驳船模型下水驳船要根据导管架的尺寸、质量和稳定性以及装船码头的水位和潮汐变化情况等进行选择。对工程中常用下水驳船的主尺度及参数进行调研,一般地,下水驳船的载质量约为长×宽×高的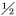

采用单体船纵向下水方式,图 1即为导管架下水的有限元仿真模型。基于时域分析法,假定驳船和导管架均为6个自由度刚体,且2个刚体通过滑道和摇臂相对运动。导管架所受的静水压力和动水压力用MORISON公式计算,驳船运动和湿表面压力通过二维切片理论求得,驳船水动力惯性力与黏性阻力使用不断修正的附加质量系数与拖曳力系数计算。下水过程的每一时间步,导管架与驳船的运动基于二者间的重力、浮力、水动力及惯性力等受力平衡进行预测。导管架和驳船的相互运动通过解耦的方法进行分析,即把导管架和驳船离散成单个体来考虑动态平衡,建立运动方程,导管架和驳船的相互作用力体现在各自的运动方程中。
|
| 图 1 导管架下水有限元仿真模型 Fig.1 Finite element model of jacket launching |
2.4 数值计算结果
为了避免重复工作,节约数值计算成本,对25种试验方案编制了参数化批处理时域分析程序,实现了程序的自动连续调用与运行,得到各个工况下泥面间隙、导管架最大纵倾、导管架最大纵向和垂向拍击速度、导管架反转和分离的时间、反转时导管架所受浮力、反转时摇臂最大反力、驳船最大纵倾、驳船最大艉吃水、驳船最大纵向拍击速度及反转时相对速度等批量数值计算结果。下水分析结果满足诺贝尔丹顿规范[14]以及项目规格书的各项技术指标要求,例如:①完整工况下,导管架底部间隙大于水深的10%;②导管架下水后,完整工况初始剩余浮力大于12%;③摇臂发生翻转时, 导管架相对于驳船的速度大于1 m/s。各试验的数值模拟结果汇总见表 2。
| 试验号 | 试验因素编号 | 试验指标 | ||||||
| A | B | C | D | 摇臂最大反力/kN | 导管架最大拍击速度/(m·s-1) | 导管架泥面间隙/m | ||
| 1 | 1 | 1 | 1 | 1 | 26 200 | 5.78 | 44.30 | |
| 2 | 1 | 2 | 2 | 2 | 25 160 | 5.37 | 43.36 | |
| 3 | 1 | 3 | 3 | 3 | 24 150 | 5.07 | 41.87 | |
| 4 | 1 | 4 | 4 | 4 | 23 200 | 4.84 | 40.71 | |
| 5 | 1 | 5 | 5 | 5 | 22 310 | 4.63 | 39.11 | |
| 6 | 2 | 1 | 2 | 3 | 25 810 | 5.19 | 40.93 | |
| 7 | 2 | 2 | 3 | 4 | 24 690 | 4.94 | 39.33 | |
| 8 | 2 | 3 | 4 | 5 | 23 820 | 4.80 | 38.75 | |
| 9 | 2 | 4 | 5 | 1 | 22 710 | 5.07 | 42.91 | |
| 10 | 2 | 5 | 1 | 2 | 19 440 | 5.08 | 37.94 | |
| 11 | 3 | 1 | 3 | 5 | 13 620 | 0.30 | 87.81 | |
| 12 | 3 | 2 | 4 | 1 | 24 190 | 5.26 | 43.17 | |
| 13 | 3 | 3 | 5 | 2 | 23 170 | 5.01 | 42.39 | |
| 14 | 3 | 4 | 1 | 3 | 20 030 | 4.48 | 38.14 | |
| 15 | 3 | 5 | 2 | 4 | 19 580 | 4.31 | 37.11 | |
| 16 | 4 | 1 | 4 | 2 | 24 660 | 5.12 | 41.69 | |
| 17 | 4 | 2 | 5 | 3 | 23 680 | 4.91 | 40.86 | |
| 18 | 4 | 3 | 1 | 4 | 20 500 | 4.44 | 38.40 | |
| 19 | 4 | 4 | 2 | 5 | 19 930 | 4.30 | 36.74 | |
| 20 | 4 | 5 | 3 | 1 | 19 170 | 4.79 | 38.17 | |
| 21 | 5 | 1 | 5 | 4 | 24 220 | 4.97 | 38.11 | |
| 22 | 5 | 2 | 1 | 5 | 20 730 | 4.51 | 37.30 | |
| 23 | 5 | 3 | 2 | 1 | 19 970 | 4.61 | 39.32 | |
| 24 | 5 | 4 | 3 | 2 | 19 660 | 4.46 | 37.39 | |
| 25 | 5 | 5 | 4 | 3 | 19 130 | 4.32 | 37.15 | |
3 正交试验结果分析 3.1 直观分析
正交试验结果的统计分析方法有直观分析法和方差分析法2种。其中,直观分析法简便直观,计算工作量小,结论可靠;而且笔者的试验是通过数值计算进行的,不存在物理模型试验的人为误差,所以选用直观分析法对正交试验的各个因素进行均值分析和极差分析,从而确定最佳下水参数组合及各因素敏感程度。直观分析法通过计算各因素的平均极差来判断因素对指标影响的主次关系,从而找出主要参数与次要参数。极差的大小用于衡量试验因素的重要性;极差值越大,说明该因素的水平变化对指标的影响越大,该因素越重要。正交试验的分析结果及极差如表 3和表 4所示。根据各因素各水平下每种试验指标的数据和求出各因素的均值ki(i=1, 2, 3, 4, 5),并计算出各因素的极差R。
| 试验指标 | 分析结果 | 试验因素 | |||
| A | B | C | D | ||
| 摇臂最大反力/kN | k1 | 24 200 | 22 900 | 21 380 | 22 450 |
| k2 | 23 290 | 23 690 | 22 090 | 22 420 | |
| k3 | 20 120 | 22 320 | 20 260 | 22 560 | |
| k4 | 21 590 | 21 110 | 23 000 | 22 440 | |
| k5 | 20 740 | 19 930 | 23 220 | 20 080 | |
| 导管架最大拍击速度/(m·s-1) | k1 | 5.14 | 4.27 | 4.86 | 5.10 |
| k2 | 5.02 | 5.00 | 4.76 | 5.01 | |
| k3 | 3.87 | 4.79 | 3.91 | 4.79 | |
| k4 | 4.71 | 4.63 | 4.87 | 4.70 | |
| k5 | 4.57 | 4.63 | 4.92 | 3.71 | |
| 导管架泥面间隙/m | k1 | 41.87 | 50.57 | 39.22 | 41.57 |
| k2 | 39.97 | 40.80 | 39.49 | 40.55 | |
| k3 | 49.72 | 40.15 | 48.91 | 39.79 | |
| k4 | 39.17 | 39.18 | 40.29 | 38.73 | |
| k5 | 37.85 | 37. 90 | 40.68 | 47.94 | |
| 试验指标 | 极差R | 因素主次 | 优水平 | |||||||||||
| A | B | C | D | A | B | C | D | A | B | C | D | |||
| 摇臂最大反力 | 4 080 | 3 760 | 2 960 | 2 480 | 1 | 2 | 3 | 4 | A3 | B5 | C3 | D5 | ||
| 导管架最大拍击速度 | 1.27 | 0.73 | 1.01 | 1.39 | 2 | 4 | 3 | 1 | A3 | B1(B5) | C3 | D5 | ||
| 导管架泥面间隙 | 11.87 | 12.67 | 9.69 | 9.21 | 2 | 1 | 3 | 4 | A3 | B1(B2, B3) | C3 | D5 | ||
由表 3和表 4可知,根据极差大小可以判断出4个因素对3个指标影响的主次顺序。对于摇臂最大反力指标,驳船初始吃水A的极差最大,驳船初始纵倾B和装船位置C的极差次之,滑动摩擦因数D的极差最小。这说明驳船初始吃水最敏感,其变化对摇臂最大反力大小的改变影响最大,驳船初始纵倾和装船位置敏感性居中,滑动摩擦因数的影响最小。对于导管架最大拍击速度指标,滑动摩擦因数D的极差最大,驳船初始吃水A和装船位置C的极差次之,驳船初始纵倾B的极差最小。这说明滑动摩擦因数最敏感,其变化对导管架最大拍击速度的影响最大,驳船初始吃水和装船位置敏感性居中,驳船初始纵倾的影响最小。对于导管架泥面间隙指标,驳船初始纵倾B的极差最大,驳船初始吃水A和装船位置C的极差次之,滑动摩擦因数D的极差最小;这说明驳船初始纵倾最敏感,其变化对导管架泥面间隙的改变影响最大,驳船初始吃水和装船位置敏感性居中,滑动摩擦因数的影响最小。
根据各指标不同水平平均值确定各因素的优化水平组合。下水过程中,导管架泥面间隙要保持安全距离,防止碰到泥面,造成结构损坏,因此应以泥面间隙的最大均值作为优选值;而驳船摇臂和导管架入水砰击力则应以各因素的最小均值作为优选值,以保证结构不被破坏。对于3项指标,A、C、D 3个因素的最优水平分别为A3、C3和D5,而因素B的优水平不一致。考虑本例中各工况导管架最小泥面间隙均接近40 m,导管架与海底之间的安全距离裕度很大,所以导管架最小泥面间隙可不作为主要控制指标。对于摇臂最大反力指标,因素B的优水平为B5;对于导管架最大拍击速度指标,因素B的优水平为B1,次优水平为B5。综合考虑,最终确定最优组合为A3B5C3D5。最终优化的下水参数如下:驳船初始吃水为8 m,驳船初始纵倾5°,装船位置75 m,滑动摩擦因数0.07。
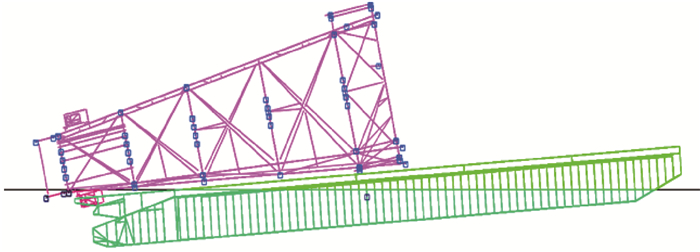
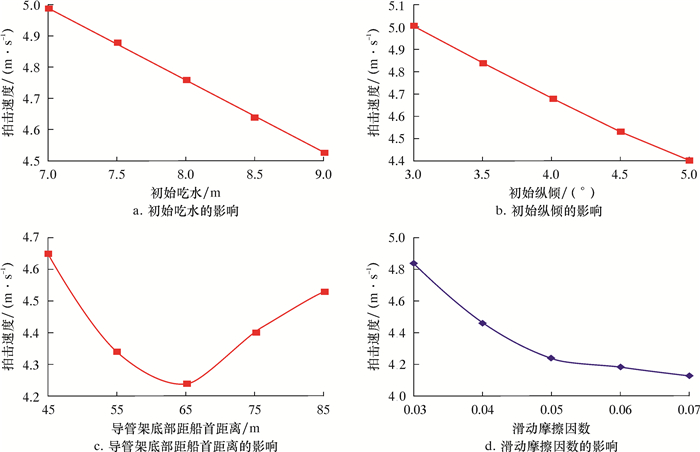
3.2 计算分析为了更直观地分析各因素对导管架下水指标的影响,根据正交试验数值计算结果分别绘制各因素对摇臂最大反力、导管架最大拍击速度和导管架与泥面间隙的影响曲线(见图 2、图 3与图 4),并进行相关理论分析。
|
| 图 2 各因素对导管架最大拍击速度影响曲线 Fig.2 Effect of various factors on the maximum slam velocity of jacket |
|
| 图 3 各因素对下水驳船摇臂最大反力影响曲线 Fig.3 Effect of various factors on the maximum reaction force of rocker |
|
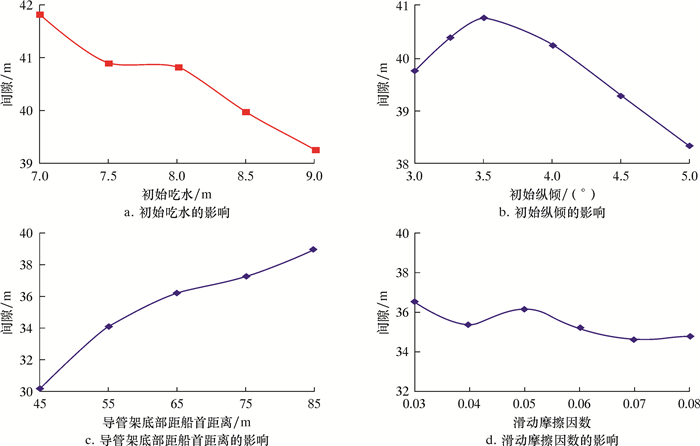
| 图 4 各因素对导管架与泥面间隙影响曲线 Fig.4 Effect of various factors on mud surface clearance of jacket |
(1) 随着驳船初始吃水的增加,导管架初始浸没入水的体积增大,开始滑移后受到的阻力随之增大,因此导管架的最大纵向和垂向拍击速度都减小,进而使导管架构件所受波浪砰击力减小;摇臂最大反力和导管架与泥面间隙也具有随着驳船初始吃水增加而减小的趋势。
(2) 因为驳船初始吃水越大,导管架拍击速度和摇臂反力越小,而且系统重心更低,从而稳定性裕度更大,所以驳船初始吃水应尽量选大值。但吃水太大也可能引起下滑力和浮力相抵消,从而导致导管架滑动停滞。因此,正交试验优选得出的8 m初始吃水参数可靠合理。
(3) 在驳船初始纵倾3.0°~3.5°范围内,随着初始纵倾增大,导管架与泥面间隙为增大趋势,在初始纵倾为3.5°时出现极值;在驳船初始纵倾3.5°~5.0°范围内,曲线的变化趋势与之前相反,即随着初始纵倾增大,导管架与泥面间隙表现为减小趋势。随着驳船初始纵倾的增加,导管架初始浸没入水体积增大,开始滑移后受到的阻力随之增大,导致导管架的最大拍击速度减小;摇臂最大反力减小。
(4) 随着导管架底部距艏距离增加,连续滑靴压摇臂长度增加,导管架在驳船上加速滑行的时间越短,获得的加速度越小,所以导管架下潜深度减小,从而导管架泥面间隙增加,摇臂最大反力增大。导管架底部距船首距离为45 m时,导管架最大拍击速度最大;随后,导管架最大拍击速度随导管架底部距船首距离的增大而减小;至导管架底部距船首距离为65 m时,导管架最大拍击速度出现最小值;之后曲线趋势改变,即随管架底部距船首距离的增大而增大。
(5) 随着滑动摩擦因数的增大,导管架与海底泥面之间的间隙总体趋势是减小,导管架在滑移过程中对驳船的作用力增大,因此导管架的最大拍击速度有显著减小。滑动摩擦因数越大,滑动所需时间越长,所以导管架入水速度越小,而且滑动摩擦因数越小(在0.03~0.05之间时),影响曲线斜率较大,说明滑动摩擦因数对导管架的最大拍击速度影响大,随着滑动摩擦因数的增大(在0.05~0.07之间时),影响曲线斜率明显减小,说明滑动摩擦因数对导管架的最大拍击速度影响变小。随着滑动摩擦因数的增大,摇臂最大反力有所增大,但变化不明显,说明滑动摩擦因数对摇臂最大反力指标的影响很小,此结论也与试验结果相符。
4 优化的下水设计方案数值计算结果对最终优化的下水工况进行三维时域分析。下水过程中导管架和驳船泥面间隙变化如图 5所示。左、右舷摇臂支反力和导管架底面左、右边杆件受力变化分别如图 6和图 7所示。由图 5可知,导管架离海底面的底部间隙为39.17 m,大于水深100 m的10%要求。由图 6可知,翻转时最大摇臂反力为导管架重力的50%,分离时为15%。以上参数均满足安装规范要求[14]。根据数值计算结果,驳船和导管架分离后向相反的方向运动,X方向的相对速度为4.0 m/s,满足安装规范要求[14]。分离时刻,摇臂转轴和导管架末端的最小间距为6.580 m,大于6.039 m的摇臂深度,满足要求。此外,根据运动速度分析,摇臂的末端与滑靴的前段有明显分离,所以导管架与驳船不会产生碰撞。计算结果表明整个下水过程安全平稳。下水轨迹最终也得到了海上施工现场的验证。
|
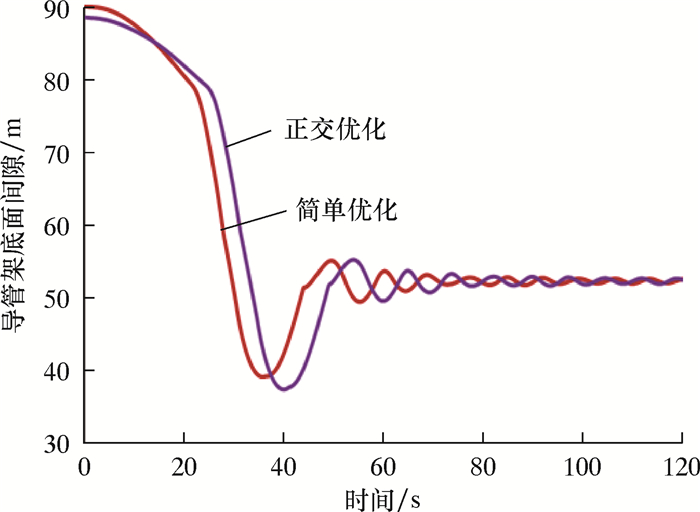
| 图 5 下水过程中导管架泥面间隙时历曲线比较 Fig.5 Comparison of time-history curves of mud clearances of jacket |
|
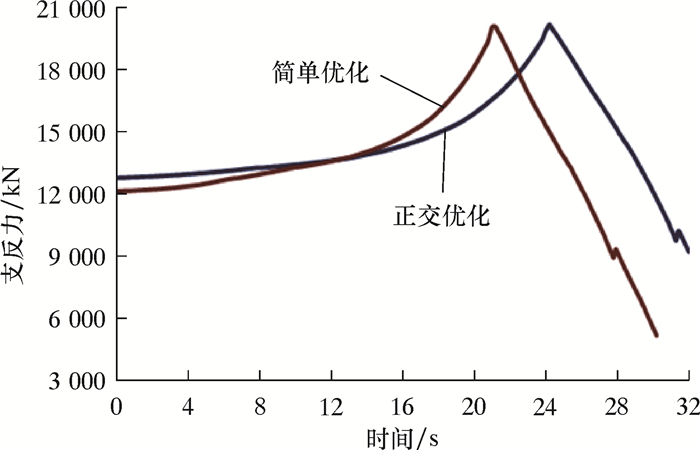
| 图 6 驳船摇臂(左、右舷)支反力时历曲线比较 Fig.6 Comparison of time-history curves of bearing reaction on barge rocker (port and starboard) |
|
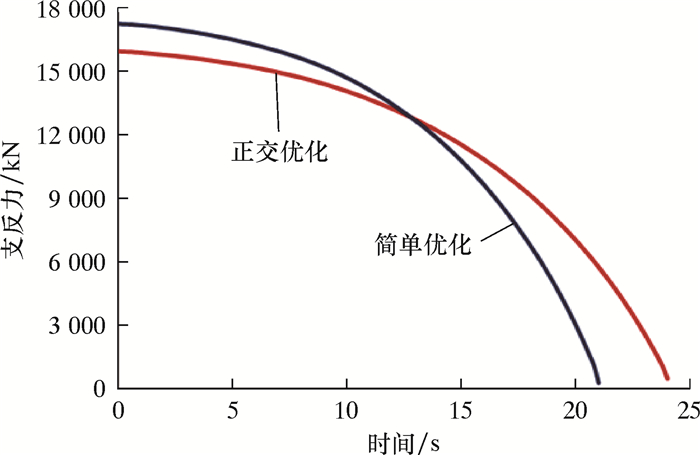
| 图 7 导管架下水左、右边杆件支反力时历曲线比较 Fig.7 Comparison of time-history curves of bearing reaction on jacket left and right side of the rod |
为了验证正交优化方法的优越性,对简单优化方案和正交优化方案进行比较。如图 5所示,2个方案的泥面间隙时历曲线基本一致,正交优化方案的导管架最小泥面间隙为37.42 m,简单优化方案的导管架最小泥面间隙为39.17 m,二者相差很小,都远远大于水深10%的最小安全距离。如图 6所示,简单优化方案驳船受力的最大值与正交优化方案相近,但正交优化方案的驳船受力曲线更平缓,持力时间更长,说明驳船摇臂受力的动力效应更小,可以有效减小摇臂自动复位对驳船尾部甲板的冲击。图 7中简单优化方案的导管架杆件最大反力为17 250 kN,而正交优化方案的导管架杆件最大反力为15 940 kN,减小了8.22%。而且,正交优化方案的导管架杆件受力时历曲线在每个时间点上的斜率更小,说明整个下水过程中正交优化方案的导管架杆件受力变化更加温和,所受动力冲击效应更小。因此,正交优化方案可以显著减小导管架下水腿的应力,从而减少结构用钢量,节约成本。
5 结论(1) 下水参数对导管架滑移下水工程的安全性和经济性起着主要的控制作用。采用正交试验设计法,可以直观地分析下水参数对下水指标的影响状况,分清各因素的影响主次。
(2) 在保持足够稳性的前提下,相比其他下水参数,增加驳船初始吃水和初始纵倾角对减少摇臂反力和导管架杆件作用力的效果更好,即初始吃水和初始纵倾是摇臂反力或导管架下水腿作用力的敏感性参数。但是,若初始吃水太小,会造成下水稳定性的裕度减小;而初始纵倾和初始吃水都过大,则可能引起导管架滑移停滞。因此需要结合多个考察指标折中选择。
(3) 滑动摩擦因数对导管架拍击速度的影响最大,采用较大的滑动摩擦因数可有效增加下水过程的稳定性和可靠性。
(4) 由正交试验法得出的优化方案比简单优化法得出的方案更加可靠和经济。
| [1] | 王建龙. 浅谈浅海桩基导管架式采油平台的施工安装[J]. 海洋技术, 2006, 25(3): 116-121. WANG J L. The construction and installation of the jacket production platform in shallow sea[J]. Ocean Technology, 2006, 25(3): 116-121. |
| [2] | 杨小龙, 杨辉, 刘波, 等. 导管架下水时的驳船总纵强度分析[J]. 船海工程, 2013, 42(3): 38-40. YANG X L, YANG H, LIU B, et al. Global strength analysis of the barge during jacket launch[J]. Ship & Ocean Engineering, 2013, 42(3): 38-40. |
| [3] | JO C H, KIM K S, LEE S H. Parametric study on offshore jacket launching[J]. Ocean Engineering, 2002, 29(15): 1959-1979. DOI: 10.1016/S0029-8018(01)00108-1 |
| [4] | CAMPBELL R B, LAMB W C, ANGEVINE D R, et al. Instrumentation of the SYU jackets for trans-pacific towand launch[C]//Offshore Technology Conference, 1991. |
| [5] | JO C H, KIM K S, KIM J H, et al. Criterion of offshore jacket launching analysis[C]//Proceedings of the International Offshore and Polar Engineering Conference, 2001. |
| [6] | 徐田甜, 张美荣. 导管架下水驳船的"浮托法"安装改造研究[J]. 船舶, 2009, 20(3): 45-49, 64. XU T T, ZHANG M R. Float-over installation modification analysis of jacket launch barge[J]. Ship & Boat, 2009, 20(3): 45-49, 64. |
| [7] | 陈忆宁, 陈刚, 杨建民, 等. 超大型导管架下水过程实测研究[J]. 海洋工程, 2014, 32(6): 9-16. CHEN Y N, CHEN G, YANG J M, et al. Research on field measurement of mega jacket launch[J]. The Ocean Engineering, 2014, 32(6): 9-16. |
| [8] | 杨晓刚. 深水导管架滑移下水的安装分析技术和设计方法[J]. 中国海上油气(工程), 2003, 15(3): 4-10. YANG X G. Launch analysis and design method for deep water jacket[J]. China Offshore Oil and Gas(Engineering), 2003, 15(3): 4-10. |
| [9] | 赵选民. 试验设计方法[M]. 北京: 科学出版社, 2005. ZHAO X M. Design of experiment[M]. Beijing: Science Press, 2005. |
| [10] | 吴群英, 林亮. 应用数理统计[M]. 天津: 天津大学出版社, 2004. WU QUN Y, LIN L. Applied mathematical statistics[M]. Tianjin: Tianjin University Press, 2004. |
| [11] | 张光发. 导管架下水运动三维数值模拟研究[D]. 大连: 大连理工大学, 2007. ZHANG F G. 3D numeric simulation for launching jacket[D]. Dalian: Dalian University of Technology, 2007. |
| [12] | 盛焕明, 陆华刚, 侯金林, 等. LW3-1中心平台导管架ODP结构方案设计[J]. 中国造船, 2013, 54(增刊2): 88-97. SHENG H M, LU H G, HOU J L, et al. Research on jacket structure schematic design issues of central platform in LW3-1 deep water gas field development[J]. Shipbuilding of China, 2013, 54(S2): 88-97. |
| [13] | 顾海军. 导管架下水驳船简介[J]. 船舶, 2007(1): 24-25, 33. GU H J. Jacket launch barge[J]. Ship & Boat, 2007(1): 24-25, 33. |
| [14] | GL NOBLE DENTON. Guidelines for the transportation and installation of steel jackets: 0028/NDI[S]. [S. l. ]: Noble Denton International Ltd., 2010. |



