2. 中国石油天然气集团公司
2. China National Petroleum Corporation
0 引言
粒子射流冲击破岩技术是一种利用高速金属粒子冲击破岩为主,以高速水射流和机械钻头破岩为辅的高效破岩方式。其工作原理是将一定比例的金属粒子注入到高压水射流管道,使高压射流与粒子充分混合,再经喷嘴的加速作用形成具有相当速度的粒子水射流,喷射冲击岩石表面从而达到破岩目的[1-2]。在粒子射流冲击破岩系统中,喷嘴起着能量转换的作用[3],将系统的压力能转换成粒子水射流的动能,从而形成高速射流,能极大地提高深井和硬地层的钻进速度。喷嘴作为粒子射流冲击破岩装置的关键部件[4-7],其加速能力和能量转换效率决定了钻进速度与破岩效果。
目前对于喷嘴的设计和仿真,多数文献通过改变喷嘴的锥角与长径比来提高喷嘴的加速能力[8]。C.M.SHEN和Z.H.HUANG等[9-10]基于有限元软件,模拟锥形喷嘴锥角和射流速度与喷嘴长径比的关系,分析了锥角和出口直径对射流速度的影响;刘成文和杨友胜等[11-12]研究了能量损失与流量系数的关系,并进行了试验验证;韩立国等[13]基于有限元软件模拟了锥直型喷嘴中粒子和水射流的加速过程;F.S.Ren等[14]基于仿真平台,研究了4种不同结构喷嘴的加速效应,分析了喷嘴长度对粒子和水射流加速度的影响。
当前对于喷嘴加速过程中的能量转换效率问题研究较少,因此有必要选择适当的喷嘴流道类型,优化喷嘴尺寸参数,提高喷嘴的能量转换效率,进而达到提高钻进速度与破岩效率的目的。笔者通过建立粒子射流在喷嘴中的加速模型,研究喷嘴收缩段长度对粒子和水射流速度的影响;同时建立喷嘴压降和能量转换效率的数学模型,分析压力降与阻力系数的关系以及能量转换效率与喷嘴收缩段长度的关系,从而优化喷嘴流道的类型与尺寸。依据优化结果,对研制的喷嘴进行了破岩试验和流场仿真。所得结论可为粒子射流冲击破岩装置的现场应用提供参考。
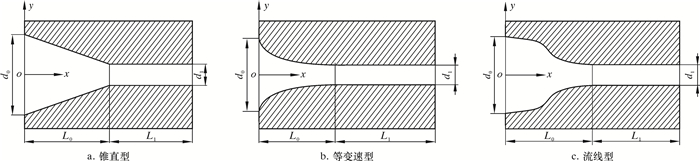
1 喷嘴流道的结构模型粒子射流冲击破岩喷嘴的结构模型是指喷嘴的流道形状与几何尺寸。目前,广泛使用的高效喷嘴根据流道形状可以分为锥直型、等变速型和流线型,结构如图 1所示。这3种喷嘴都由收缩段和圆柱段组成。
|
| 图 1 不同类型喷嘴的结构示意图 Fig.1 Structural schematic of different types of nozzles |
1.1 喷嘴流道的曲线方程
锥直型喷嘴收缩段的轮廓方程为:

|
(1) |
等变速型喷嘴收缩段的流道母线方程为[15]:
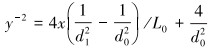
|
(2) |
流线型喷嘴收缩段的流道曲线方程为[15]:
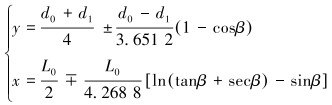
|
(3) |
式中:β为液流方向与y轴的夹角。
1.2 喷嘴结构的参数要求根据现场要求及前期研究结果[16-17],喷嘴的入口直径为15 mm,出口直径为4 mm,总长度不超过55 mm。喷嘴的材质为硬质合金,其表面粗糙度值取0.01 mm。根据现场试验要求,喷嘴入口处钻井液流速可达到10~15 m/s,最大工作压力32 MPa,钻井液密度为1 200 kg/m3,钻井液的动力黏度为1.72×10-5 Pa·s,钢质粒子的密度为7 850 kg/m3。通过改变喷嘴收缩段长度与圆柱段长度来研究喷嘴的加速能力和能量转换效率,从而选择合理的尺寸参数,提高冲击破岩效率。
2 建模与数值模拟基于3种组合型喷嘴,建立粒子水射流在喷嘴流道内的加速模型和能量转换效率模型。在喷嘴总长度一定的条件下,通过改变喷嘴收缩段长度可求得不同收缩段下粒子的喷射速度,比较不同类型喷嘴的加速能力,选择合适的喷嘴类型;根据粒子加速模型和能量转效率,选择最优的收缩段长度,为喷嘴的优化设计提供依据。
2.1 喷嘴收缩段粒子和水射流的加速模型粒子与水射流在到达喷嘴之前,首先经历高压管线的加速作用。由于管线较长,粒子和水射流能充分混合,在进入喷嘴之前,粒子速度可近似等于钻井液流速。当粒子和水射流进入喷嘴后,由于喷嘴截面积的变化,流体速度发生明显改变,流动状态为紊流。以截面上的平均速度代替该截面的速度分布,则喷嘴收缩段任意截面坐标(x, y)处钻井液的速度uf可表示为:

|
(4) |
式中:u0为钻井液在喷嘴入口处的速度,d0为喷嘴的入口直径。
粒子在喷嘴中受到的作用力包括Stoke黏性阻力、附加质量力、压力梯度力、Magnus力以及Saffman升力。由于粒子为刚体材料,且颗粒受钻井液的黏性制约,粒子射流的流速梯度较大,旋转速度较小,所以Magnus力和Saffman升力可以忽略[18]。根据牛顿第二定律,收缩段流场中的粒子运动方程为:
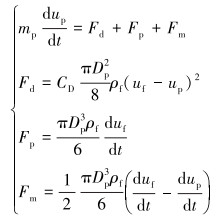
|
(5) |
式中:up为粒子在喷嘴收缩段的运动速度,mp为粒子质量,Fd为粒子在流场中受到的黏性阻力,CD为黏性阻力系数,Dp为粒子直径,ρf为钻井液密度,Fp为粒子在流场中受到的附加质量力,Fm为粒子在流场中受到的压力梯度力。
流体雷诺数在103~105之间,取CD=0.45。对方程组(5)进行整理可得:
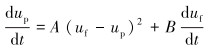
|
(6) |
式中: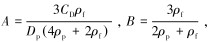
由于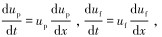
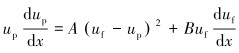
|
(7) |
粒子射流经过喷嘴收缩段的加速作用后,钻井液的速度不再发生变化,但是由于粒子加速要比钻井液慢,粒子速度明显滞后于钻井液速度,所以在高速钻井液的携带作用下粒子则会继续加速。
钻井液在喷嘴圆柱段的速度可以由式(8)求得:

|
(8) |
式中:uf1为钻井液在喷嘴圆柱段的速度,d1为喷嘴出口直径。
粒子在喷嘴圆柱段中的速度方程可表示为:

|
(9) |
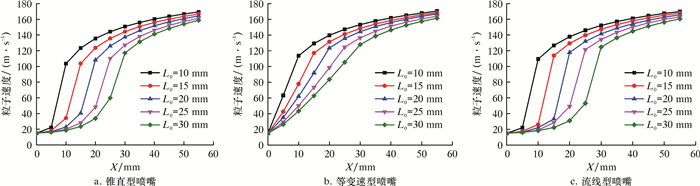
为了解喷嘴在不同收缩段长度下粒子速度的变化趋势,对式(7)和式(9)进行迭代运算,求得3种喷嘴的粒子速度随横坐标X变化的曲线,如图 2所示。由图可知,3种喷嘴的粒子速度变化都呈逐渐增加趋势,锥直型和流线型的增长趋势为先缓慢再急剧后缓和的趋势,等变速型则为先急剧后缓和的趋势。由图还可以看出,收缩段长度越小,喷嘴出口处的粒子速度越高。
|
| 图 2 3种喷嘴中粒子的速度随横坐标变化曲线 Fig.2 The particle velocities along the X-coordinate in the 3 kinds of nozzles |
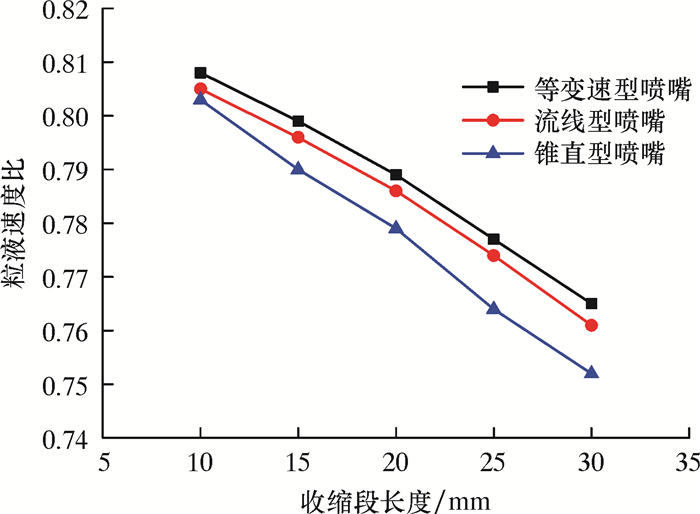
根据计算出的粒子出口速度和钻井液出口速度,可得不同喷嘴的粒液速度比ξ(ξ=up1/uf1)与喷嘴收缩段长度的关系曲线,如图 3所示。由图可知,粒液速度比随喷嘴收缩段长度的增加而减小,且当收缩段长度一定时,等变速型喷嘴的粒液速度比值最高。在加工过程中,对于内径较小且圆柱段较长的喷嘴制造较为困难,因此在满足冲击破岩要求的基础上,应尽量避免圆柱段太长[19]。根据设计要求,当粒液速度比在0.8左右时,即可满足破岩要求,此时喷嘴收缩段长度应小于20 mm。综合考虑,选取喷嘴收缩段长度L0为15 mm。
|
| 图 3 粒液速度比与收缩段长度关系曲线 Fig.3 The relationship between the particle-liquid velocity ratio and the length of the contraction section |
2.3 喷嘴压降模型和能量转换效率模型
当钻井液进入钻头喷嘴后,首先经过喷嘴收缩段的加速作用,然后进入喷嘴圆柱段。应用流体力学分析喷嘴的射流过程[20],钻井液流经喷嘴的阻力hw主要包括由收缩阻力hj和沿程阻力hf,计算公式为:
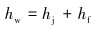
|
(10) |
喷嘴的收缩阻力hj是指钻井液流经喷嘴收缩段时受到的阻力,计算公式为:
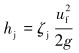
|
(11) |
式中:ζj为局部阻力系数,g为重力加速度。
由于局部阻力系数ζj与喷嘴的收缩段形状密切相关,其值大多根据试验进行测定或根据经验公式来确定[19]。
沿程阻力hf主要包括收缩段沿程阻力hf1和圆柱段沿程阻力hf2,即有:
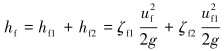
|
(12) |
式中:ζf1为收缩段沿程阻力系数,ζf2为圆柱段沿程阻力系数。
根据达西公式,收缩段沿程阻力系数ζf1计算式为:

|
(13) |
式中:λ为沿程阻力因数。
圆柱段的沿程阻力系数ζf2的表达式为:

|
(14) |
沿程阻力因数λ与喷嘴的表面粗糙度和流体流态相关,可查阅尼古拉兹试验结果[18]。
喷嘴的总阻力系数ζ表达式为:
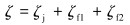
|
(15) |
根据钻井液流动的能量方程可推导出喷嘴流量系数C与喷嘴总阻力系数ζ的关系为:
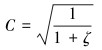
|
(16) |
喷嘴的压力降是指喷嘴入口压力和出口压力的差值,是决定粒子水射流动能的重要参数。喷嘴的压力降Δp的表达式为:

|
(17) |
式中:Q为钻井液流量,A0为喷嘴入口的横截面积,n为喷嘴数量。
从式(15)~式(17)可以看出,喷嘴的总阻力系数ζ与流量系数C成反比,流量系数越大,阻力系数越小,同等条件下的压力降就越小。
喷嘴入口处的水功率Ni为:
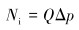
|
(18) |
喷嘴出口处的水功率No为:
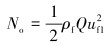
|
(19) |
在粒子射流冲击破岩系统中,喷嘴作为能量的转换元件,其性能可由能量转换效率η表示:
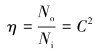
|
(20) |
由式(20)可知,喷嘴的能量转换效率等于流量系数的平方。
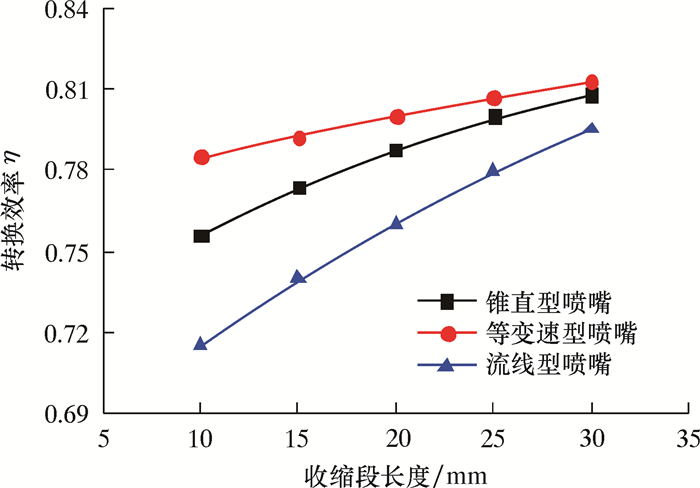
3种喷嘴的能量转换效率随喷嘴收缩段长度变化曲线如图 4所示。
|
| 图 4 能量转换效率与收缩段长度关系曲线 Fig.4 The relationship between energy conversion efficiency and the length of the contraction section |
随着喷嘴收缩段长度的增加,其能量转换效率逐渐升高。当收缩段长度一定时,等变速型喷嘴的能量转换效率最高。由于喷嘴压降与喷嘴流量系数成反比,在满足破岩要求的条件下,需要选用能量转换效率最高的喷嘴,即粒子射流冲击破岩喷嘴选用等变速型。
3 喷嘴的参数优化及流场仿真 3.1 参数优化根据粒子水射流在喷嘴中的加速机理和能量转换效率的计算结果,喷嘴的流道形状选用等变速型。设计的喷嘴尺寸参数为:收缩段长度15 mm,圆柱段长度40 mm,如图 5所示。

|
| 图 5 喷嘴的结构与尺寸参数 Fig.5 The structure and size parameter of the nozzle |
由于喷嘴中的粒子水射流速度较高,冲蚀磨损比较严重,所以材质选用硬度较高、抗磨损和抗腐蚀性好的硬质合金。
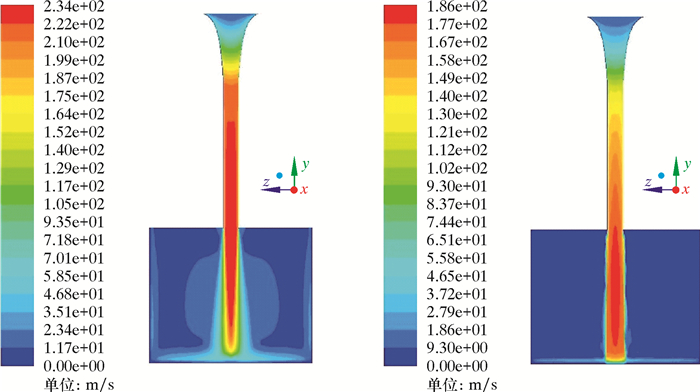
3.2 流场仿真为模拟所设计的喷嘴内粒子的加速情况及井底流场的流动规律,利用计算流体力学对喷嘴内部流场进行仿真分析。流场仿真过程中,边界条件采用速度入口和自由出流,入口处粒子和钻井液的速度为15 m/s,粒子的体积分数为0.2%。仿真计算采用标准的k-ε方程和欧拉模型[21],求解方法采用PHASE COUPLE SIMPLE算法。经迭代仿真,等变速型喷嘴中钻井液和粒子的速度分布如图 6所示。
|
| 图 6 等变速型喷嘴中钻井液和粒子的速度云图 Fig.6 The velocity distribution of drilling fluid and particles in the constant-acceleration nozzle |
钻井液的加速过程主要集中在喷嘴收缩段,圆柱段中钻井液的速度基本不变,而粒子的加速过程贯穿于喷嘴收缩段和圆柱段。这是因为粒子的加速滞后于流体,圆柱段中钻井液的流速基本不变,但是其速度明显高于粒子速度,因此粒子在高速流体的携带作用下会继续加速。钻井液和粒子离开喷嘴后,会形成喷射等速核,钻井液的速度逐渐减小,而粒子则是先增加再逐渐减小。
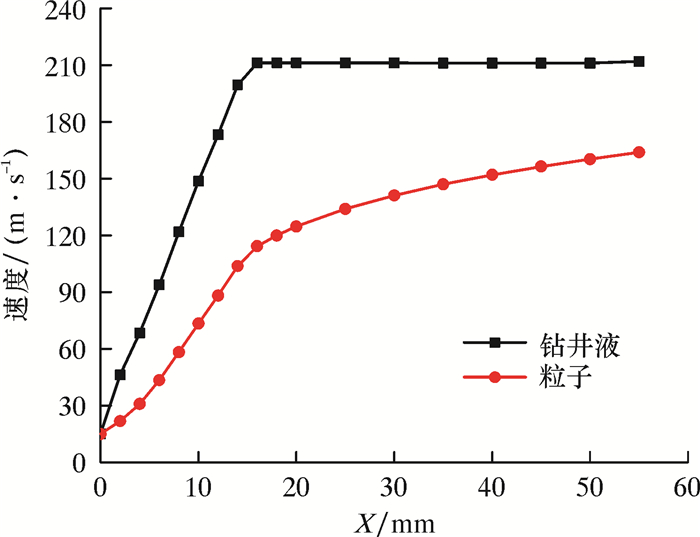
等变速型喷嘴轴线上钻井液和粒子的平均速度分布曲线如图 7所示。喷嘴轴线上钻井液最大平均速度为214 m/s,而粒子最大平均速度为162 m/s。数值模拟与仿真结果对比如表 1所示。
|
| 图 7 喷嘴轴线上钻井液和粒子平均速度分布曲线 Fig.7 The average velocity distribution of drilling fluid and particles on the axis of the nozzle |
| 项目 | 粒子速度/(m·s-1) | 钻井液速度/(m·s-1) |
| 数值模拟 | 166.8 | 210.9 |
| 仿真结果 | 161.5 | 212.5 |
| 误差/% | 3.280 | 0.753 |
两者的对比误差很小,表明经过该喷嘴加速后粒子的速度值可以达到破岩要求。
4 试验研究为验证所设计的等变速型喷嘴的破岩性能,基于自主研制的粒子射流冲击破岩装置和参数优化后的喷嘴开展了破岩试验。
采用优化设计的等变速型喷嘴进行一系列冲击破岩试验[14],试验过程中采用的高压钻井泵参数如表 2所示。泵压和工作压力可由压力表测得。泵的排量可由泵转速求得。
| 额定压力/MPa | 额定流量/(L·min-1) | 泵速/(r·min-1) | 柱塞直径/mm | 柱塞行程/mm |
| 32 | 165 | 80~180 | 70 | 80 |
试验数据与理论值的对比如图 8所示。由图可知,试验值与理论值基本一致,证明了压降数学模型的适用性,同时表明参数优化的等变速型喷嘴达到了冲击破岩要求。

|
| 图 8 试验数据与理论值的对比结果 Fig.8 Comparison of experimental data and theoretical values |
5 结论
(1) 喷嘴出口的粒子速度随收缩段长度增加而降低,根据粒液速度比与破岩要求,设计喷嘴收缩段长度为15 mm,圆柱段长度为40 mm。
(2) 喷嘴的压降与阻力系数成反比,喷嘴的能量转换效率随收缩段长度的增加而减小,当其他条件一定时,等变速型喷嘴的能量转换效率最高,因此选用等变速型喷嘴。
(3) 在参数优化的基础上对喷嘴进行了流场仿真分析,研制了等变速型喷嘴并开展了粒子射流冲击破岩试验,验证了粒子和流体的加速性能。冲击破岩试验结果表明:该喷嘴可以应用于粒子射流冲击钻井破岩工艺。
| [1] | HARDISTY T. Particle drilling pulverizes hard rocks[J]. American Oil & Gas Reporter, 2007, 50(7): 86-89. |
| [2] | 邢雪阳, 徐依吉, 杨勇, 等. 粒子冲击钻井钻头内流道冲蚀特性研究[J]. 石油机械, 2015, 43(11): 39-43. XING X Y, XU Y J, YANG Y, et al. Erosion characteristics of inner flow channels of the particle impact drilling bit[J]. China Petroleum Machinery, 2015, 43(11): 39-43. |
| [3] | 周爱照, 刘永旺, 赵健, 等. 粒子冲击钻井系统中粒子分选装置的研制[J]. 天然气工业, 2014, 34(8): 97-101. ZHOU A Z, LIU Y W, ZHAO J, et al. Research and development of the particle separation device in a particle impact drilling system[J]. Natural Gas Industry, 2014, 34(8): 97-101. |
| [4] | 易灿, 李根生. 喷嘴结构对高压射流特性影响研究[J]. 石油钻采工艺, 2005, 27(1): 16-19. YI C, LI G S. Study of the influence of the nozzle structure on waterjet characteristics[J]. Oil Drilling & Production Technology, 2005, 27(1): 16-19. |
| [5] | 任福深, 马若虚, 程晓泽, 等. 粒子冲击钻井技术研究进展及关键问题[J]. 石油矿场机械, 2014, 43(7): 20-25. REN F S, MA R X, CHENG X Z, et al. Research progress and key problems of particle impact drilling technology[J]. Oil Field Equipment, 2014, 43(7): 20-25. |
| [6] | 田志欣, 王国华, 李源源, 等. 喷嘴直径匹配对PDC钻头流场特性影响[J]. 钻采工艺, 2017, 40(5): 8-10. TIAN Z X, WANG G H, LI Y Y, et al. Effects of PDC bit's nozzle diameter on flow field characteristics[J]. Drilling & Production Technology, 2017, 40(5): 8-10. |
| [7] | 姚利明, 刘巨保, 韩雪, 等. 井下喷射孔结构压降计算中流量系数的探讨[J]. 石油钻采工艺, 2017, 39(2): 169-175. YAO L M, LIU J B, HAN X, et al. Discussion on flow rate coefficient used for the calculation of downhole jet orifice pressure drop[J]. Oil Drilling & Production Technology, 2017, 39(2): 169-175. |
| [8] | 纪国栋, 汪海阁, 王灵碧, 等. 粒子冲击钻井钻头喷嘴流场数值模拟研究[J]. 石油机械, 2012, 40(10): 18-21, 58. JI G D, WANG H G, WANG L B, et al. Numerical simulation research on the bit nozzle flow field of particle impact drilling[J]. China Petroleum Machinery, 2012, 40(10): 18-21, 58. |
| [9] | SHEN C M, LIN B Q, MENG F W. Structure optimization and application of conical convergence high-pressure jet nozzle[J]. Advanced Materials Research, 2011, 228/229: 1001-1006. DOI: 10.4028/www.scientific.net/AMR.228-229 |
| [10] | HUANG Z H, XIE Y. Research on structural parameters of conical nozzle[J]. Applied Mechanics and Materials, 2011, 84: 368-372. |
| [11] | 刘成文, 李兆敏. 锥形喷嘴流量系数及水力参数的理论计算方法[J]. 钻采工艺, 2000, 23(5): 1-3. LIU C W, LI Z M. A theoretical calculation method for flow rate coefficient and hydraulic parameters of conical nozzle[J]. Drilling & Production Technology, 2000, 23(5): 1-3. |
| [12] | 杨友胜, 张建平, 聂松林. 水射流喷嘴能量损失研究[J]. 机械工程学报, 2013, 49(2): 139-145. YANG Y S, ZHANG J P, NIE S L. Energy loss of nozzles in water jet system[J]. Journal of Mechanical Engineering, 2013, 49(2): 139-145. |
| [13] | 韩立国, 石超, 周龙昌, 等. 粒子冲击钻头喷嘴研究[J]. 钻采工艺, 2014, 37(2): 70-74. HAN L G, SHI C, ZHOU L C, et al. Research on the bit nozzles of particle impact drilling[J]. Drilling & Production Technology, 2014, 37(2): 70-74. |
| [14] | REN F S, MA R X, CHENG X Z. Simulation of particle impact drilling nozzles based on FLUENT[J]. Advanced Materials Research, 2014, 988: 475-478. DOI: 10.4028/www.scientific.net/AMR.988 |
| [15] | 刘永建. 喷射钻井技术理论基础与实践[M]. 哈尔滨: 黑龙江科学技术出版社, 1993, 313-343. LIU Y J. Theoretical basis and practice of jet drilling technology[M]. Harbin: Heilongjiang Science and Technology Press, 1993, 313-343. |
| [16] | 任福深, 程晓泽, 李洋, 等. 粒子射流耦合冲击破岩建模与实验分析[J]. 工程力学, 2017, 34(2): 249-256. REN F S, CHENG X Z, LI Y, et al. Mathematical modeling and experimental analysis of coupled particle and jet flow rock breaking[J]. Engineering Mechanics, 2017, 34(2): 249-256. |
| [17] | REN F S, WANG B J, CHENG X Z, et al. Design and experimental investigation about a simulation device for particle impact rock breaking[C]//Proceedings Volume 9302, International Conference on Experimental Mechanics 2014. Singapore, Singapore: SPIE, 2015: 93021X. |
| [18] | 王明波, 王瑞和. 湍流对磨料水射流中磨料颗粒受力的影响[J]. 中国机械工程, 2012, 23(8): 972-974. WANG M B, WANG R H. Effects of turbulence on drag force of abrasive particles in abrasive water jetting[J]. China Mechanical Engineering, 2012, 23(8): 972-974. |
| [19] | 史怀忠, 李根生, 黄中伟, 等. 水力喷射压裂用喷嘴耐冲蚀试验方法研究[J]. 石油机械, 2016, 44(12): 83-86. SHI H Z, LI G S, HUANG Z W, et al. Study on erosion resistance experimental method for hydra-jet fracturing nozzle[J]. China Petroleum Machinery, 2016, 44(12): 83-86. |
| [20] | 李诗久. 工程流体力学[M]. 北京: 机械工业出版社, 1980, 79-156. LI S J. Engineering fluid mechanics[M]. Beijing: China Machine Press, 1980, 79-156. |
| [21] | 王治国, 冉亚楠, 隆世明, 等. 水力喷射工具射孔过程液固两相流冲蚀数值模拟[J]. 石油机械, 2015, 43(9): 61-65. WANG Z G, RAN Y N, LONG S M, et al. Numerical simulation of slurry flow erosion in perforating by hydraulic jetting tool[J]. China Petroleum Machinery, 2015, 43(9): 61-65. |


