0 引言
涡轮钻具是一种重要的井下动力钻具,常用于深井、超深井和高温、高压作业环境。涡轮钻具的性能与涡轮定子和转子叶型的水力性能密切相关,改进涡轮钻具定子和转子叶型的水力性能一直是涡轮钻具优化的研究核心。
现阶段针对涡轮钻具叶型的优化主要有2个思路,即叶型造型方式的优化和叶型造型参数的优选[1-6]。在优选叶型造型参数时往往通过改变某一型号叶型的单一参数来构造一系列叶型,并对比不同叶型方案的CFD或者试验结果筛选出最佳参数。使用这种方法,前人对环流系数、轴间隙以及叶栅节距等设计参数进行了优化,并给出了参数推荐范围[7-8]。但这样的方法需要人工重复进行叶型构造、分网以及数值模拟,不但自动化程度低,而且由于是人工进行寻优,优化结果精度往往有限。笔者采用NUMECA软件包中的FINE/Design 3D优化平台,基于BP人工神经网络与遗传基因算法对某型号ø178 mm涡轮钻具转子叶型安装角进行优化设计,以期提高涡轮钻具的水力性能。
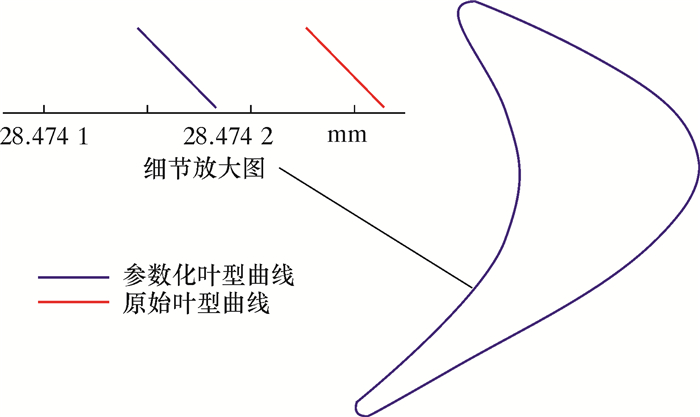
1 叶片的参数化造型涡轮叶片的参数化造型通过NUMECA软件包中的Autoblade模块,基于S1、S2流面理论实现。初始转子叶型采用五次多项式方法进行设计[2],拟合结果如图 1所示。图中红线代表初始叶型,蓝线代表参数化叶型。根据拟合结果可知,参数化叶型对原始叶型的拟合误差在1×10-3 mm内,拟合效果良好。
|
| 图 1 参数化叶型与初始叶型对比 Fig.1 Comparison of parametric blade with initial blade |
2 优化策略
优化算法首先通过CFD计算生成包含叶型与对应水力性能的样本库,并通过样本库训练得到BP神经网络。遗传算法根据BP神经网络预测结果进行寻优,并对最优结果进行CFD计算。随后将预测最优叶型及CFD结果作为新的样本对BP神经网络进行校验。重复该过程,当神经网络预测值符合CFD计算结果时则认为基本收敛,此时的优化结果即为最终优化结果。
2.1 样本库生成计算网格采用NUMECA软件包中AutoGrid模块生成的4OH型网格。数值计算采用NUMECA软件包中的Fine模块,应用有限体积法求解圆柱坐标系下三维定常N-S方程组,使用Spalart-Allmaras(S-A)湍流模型[9-10]。考虑到涡轮钻具工作实际情况,边界条件设置为定流量边界。优化时仅针对设计工况,控制进出口边界为设计流量28 L/s,设计转速800 r/min不变。
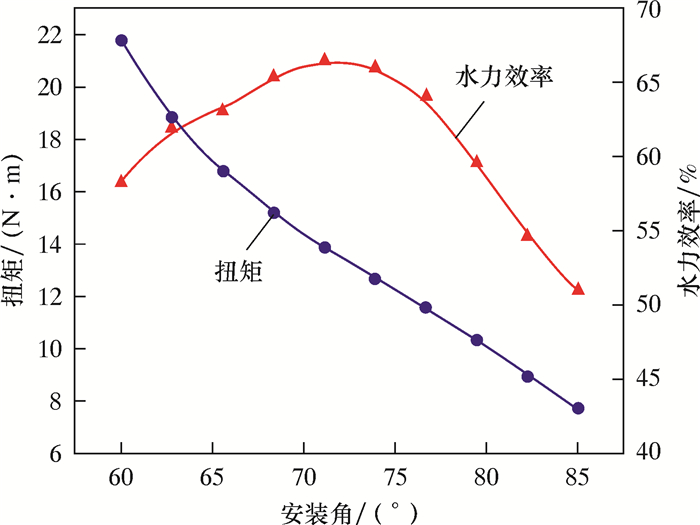
安装角设计初始值75°,变化范围60°~85°,采用full factorial方法生成样本。网格划分成功并完成CFD计算的有效样本数为10,初始样本库分布如图 2所示。从图可以看出,随着转子安装角的增大,设计工况下单级涡轮输出扭矩逐渐下降,而水力效率则呈抛物线形状变化。
|
| 图 2 样本库分布 Fig.2 Sample date base distribution |
2.2 BP神经网络与遗传算法设置
优化采用具有3个隐藏层的BP神经网络,使用2.1节中生成样本库对神经网络进行训练。优化时各节点训练次数为10万次。同时为了避免不同输出参数间的干扰,优化时针对扭矩与水力效率分别构建独立的神经网络。
优化参数为涡轮水力效率与单级扭矩,为多目标优化问题,因此引入罚函数项,将不同目标的罚函数与原始目标函数相加得到目标函数。该目标函数为遗传算法的适应度。目标函数计算如下[11]:
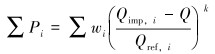
|
(1) |
式中:Qimp根据样本库及优化目标人工给定;Q是计算值;Qref为无量纲参考值;k为罚函数指数;W为加权因子。
优化时设置2个目标参数的加权因子相同,均为2,每次优化计算进化24代。
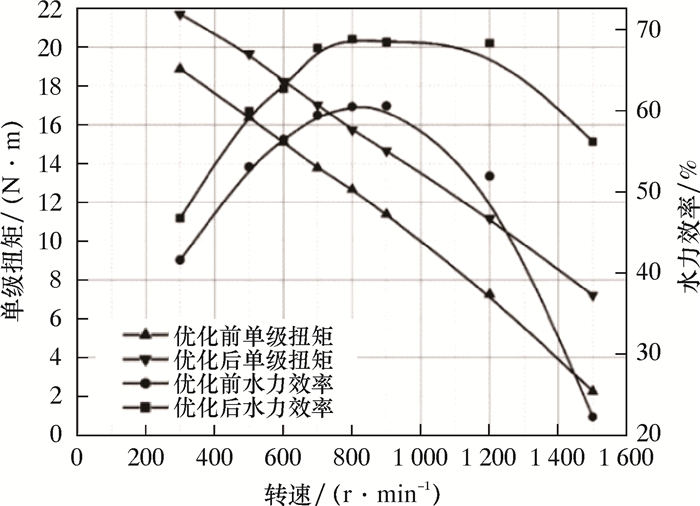
3 优化结果及分析 3.1 优化结果经过30次循环优化,转子安装角α由75.00°调整为67.44°。优化后,单级涡轮扭矩由12.67 N·m增大到15.73 N·m;水力效率由60.51%提高到68.80%,优化效果明显。为了进一步验证优化结果,对转速从300 r/min增加到1 500 r/min的优化方案水力性能进行数值模拟。数值模拟参数设置同2.1节。优化前、后单级涡轮水力性能对比如图3所示。通过性能曲线对比,优化后涡轮输出扭矩明显增加,水力效率明显提高。
|
| 图 3 优化前、后涡轮水力性能对比 Fig.3 Hydraulic performance of turbodrill before and after optimization |
3.2 流场分析
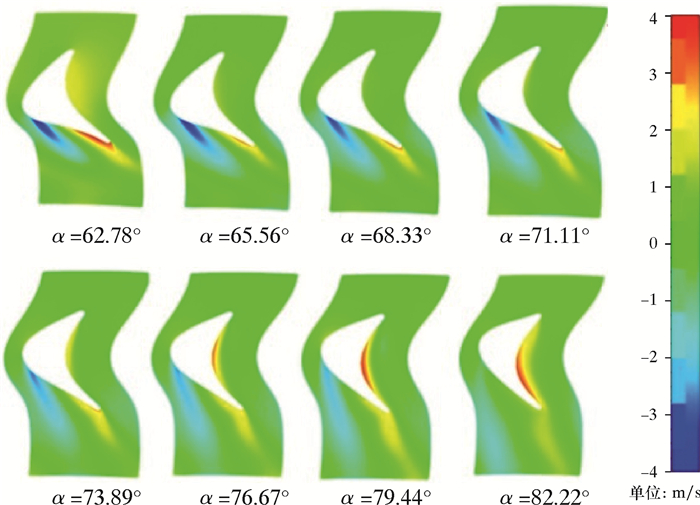
图 4为样本库中不同安装角的转子流道径向速度分布云图。从图可以看出,安装角增大,转子吸力面后缘以及叶片尾缘的二次流发展得到了有效抑制[12],水力损失减小,涡轮水力效率提高。但是随着安装角的继续增大,转子压力面的二次流得到了充分发展,当压力面水力损失增加量大于吸力面减少量时,叶型整体水力损失增大,涡轮水力效率开始下降。因而随着转子安装角增大,涡轮水力效率先升高后降低。
|
| 图 4 不同安装角的转子流道径向速度云图 Fig.4 The radial velocity distribution in the flow channel of the rotor with different installation angles |
图 5给出了优化前、后单级涡轮径向速度分布云图。从图可以看出,优化后转子叶型的二次流得到了有效抑制。对比优化前、后可以发现,优化前转子水力损失在样本中已经较低,而优化后则进一步降低了转子的水力损失。这也说明了本次优化是在初始优化方案的基础上再优化,精度较高。
|
| 图 5 优化前、后转子流道径向速度云图 Fig.5 The radial velocity of the rotor flow channel before and after optimization |
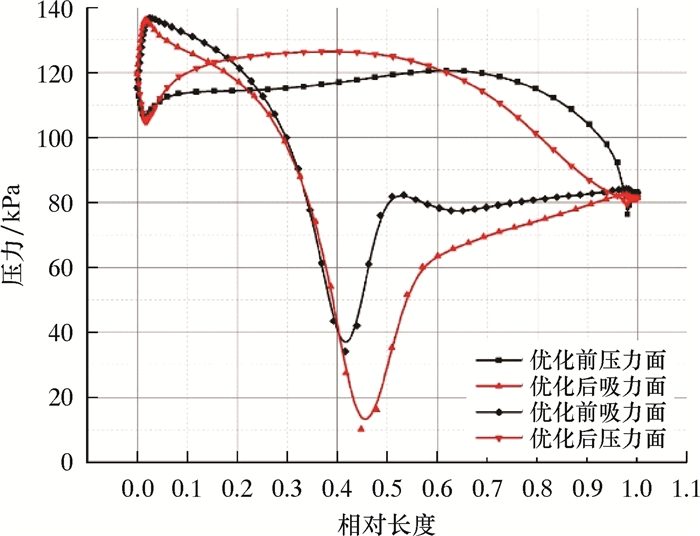
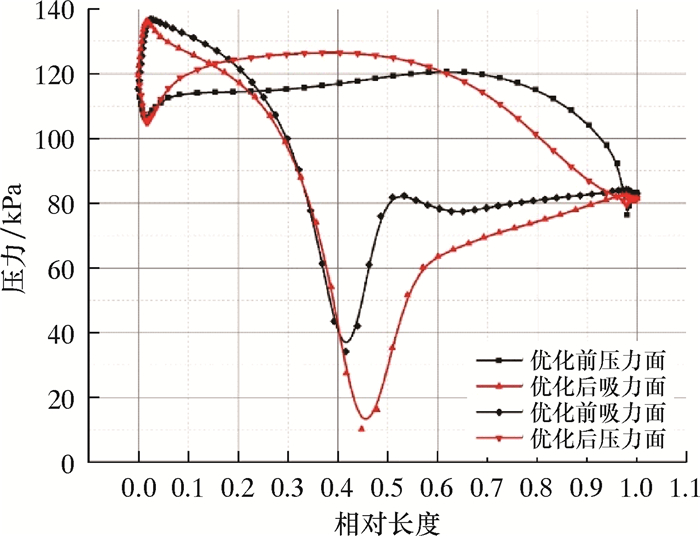
图 6是优化前、后转子50%叶高处压力分布对比。流体进入涡轮后,在前缘分流,一部分流体沿压力面流动,一部分沿吸力面流动。由于流体在叶片不同表面的流动特性不同,在叶片压力面与吸力面间产生压差,在压差的作用下,涡轮转子带动主轴旋转并做功。因而,叶片2条压力线围成的面积越大,则压力面与吸力面间压差越大,输出扭矩越高。经过优化,压力线在前缘相交面积减小且2条压力线围成的面积明显增大。由此可见,优化后转子叶型的输出扭矩增加,性能更优。
|
| 图 6 优化前、后转子压力分布 Fig.6 Pressure distribution of rotor before and after optimization |
4 结论
(1) 采用FINE/Design 3D优化平台与BP神经网络、遗传基因算法相结合的优化方法,优化流程自动化程度和精确度均较高,为涡轮叶片优化设计提供了有力手段。
(2) 在一定范围内,随着转子安装角的增大,涡轮扭矩逐渐降低,水力效率先升高后降低,呈抛物线状变化。
(3) 基于BP神经网络与遗传基因算法的涡轮转子安装角优化设计方法有效抑制了转子工作时二次流的产生,并增大了涡轮转子压力面与吸力面之间的压差。对于一级涡轮的输出扭矩提高了3.06 N·m,水力效率提升了8.29%,优化效果良好。该研究方法可为今后涡轮叶片的优化设计提供新的思路。
| [1] | 张晓东, 余世敏, 龚彦, 等. 基于Bezier曲线的涡轮叶片参数化造型及优化设计[J]. 机械强度, 2015, 37(2): 266-271. ZHANG X D, YU S M, GONG Y, et al. Modeling and optimization for turbine blades based on Bezier curve[J]. Journal of Mechanical Strength, 2015, 37(2): 266-271. |
| [2] | 冯进, 符达良. 涡轮钻具涡轮叶片造型设计新方法[J]. 石油机械, 2000, 28(11): 9-12. FENG J, FU D L. New design method of turbine blade shape of turbodrill[J]. China Petroleum Machinery, 2000, 28(11): 9-12. DOI: 10.3969/j.issn.1001-4578.2000.11.003 |
| [3] | 徐斌云. 井下轴流涡轮水动力性能研究及CAD技术[D]. 荆州: 长江大学, 2012. XU B Y. The axial-flow turbine downhole's hydrodynamic performance research and CAD technology[D]. Jingzhou: Yangtze University, 2012. |
| [4] | 朱林, 王龙. 一种涡轮钻具叶片叶型参数化设计方法[J]. 机械研究与应用, 2015, 28(4): 174-176. ZHU L, WANG L. A method of parametric design for turbine drill blade profile[J]. Mechanical Research & Application, 2015, 28(4): 174-176. |
| [5] | 董小虎. 适用于连续管的小尺寸涡轮钻具叶型研究[D]. 荆州: 长江大学, 2014. DONG X H. Turbine blade research of small size turbodrill apply to coiled tubing[D]. Jingzhou: Yangtze University, 2014. |
| [6] | 谭春飞, 张升峰, 张仁龙, 等. 涡轮叶片型线结构对叶栅流场的影响研究[J]. 石油机械, 2012, 40(12): 6-9. TAN C F, ZHANG S F, ZHANG R L, et al. Research on the effect of turbine blade profile line structure on cascade flow field[J]. China Petroleum Machinery, 2012, 40(12): 6-9. |
| [7] | 赵洪波. 涡轮钻具涡轮叶片设计及水力性能仿真优化研究[D]. 北京: 中国地质大学(北京), 2012. ZHAO H B. Study on turbodrill blade design and hydraulic performance simulation and optimization[D]. Beijing: China University of Geosciences (Beijing), 2012. |
| [8] | 戴静君, 姜义忠, 董守平. PIV技术在涡轮叶栅内流场试验中的应用[J]. 流体力学实验与测量, 2003, 17(4): 68-70. DAI J J, JIANG Y Z, DONG S P. The application of particle image velocimetry to fluid experimentation in a turbine cascade[J]. Experiments and Measurements in Fluid Mechanics, 2003, 17(4): 68-70. |
| [9] | 杨敏官, 陆胜, 高波, 等. 叶片厚度对混流式核主泵叶轮能量性能影响研究[J]. 流体机械, 2015, 43(5): 28-32. YANG M G, LU S, GAO B, et al. Influence of blade thickness on energy performance of mixed flow nuclear main pump[J]. Fluid Machinery, 2015, 43(5): 28-32. |
| [10] | 冯进, 张慢来, 刘孝光, 等. 应用CFD软件模拟ø115 mm涡轮钻具机械特性[J]. 天然气工业, 2006, 26(7): 71-73. FENG J, ZHANG M L, LIU X G, et al. CFD simulation of mechanical performance of turbodrill with diameter of 115 minimeter[J]. Natural Gas Industry, 2006, 26(7): 71-73. |
| [11] | 郭然, 贾力平, 樊小莉, 等. NUMECA系列教程[M]. 北京: 机械工业出版社, 2013. GUO R, JIA L P, FAN X L, et al. The tutorial series of NUMECA[M]. Beijing: China Machine Press, 2013. |
| [12] | 谭春飞, 汪伟, 黄志良, 等. 叶片数对水力减速级涡轮输出性能的影响研究[J]. 石油机械, 2017, 45(2): 6-9. TAN C F, WANG W, HUANG Z L, et al. Study on the performance of hydraulic reduction turbineby varying the blade number[J]. China Petroleum Machinery, 2017, 45(2): 6-9. |



