2. 中国石油大学(华东)
2. China University of Petroleum(Huadong)
0 引言
目前,海上防砂技术主要包括多层简易防砂、水平井砾石充填防砂及一次多层砾石充填防砂技术。由于嵌装在封隔器坐封工具上的密封与封隔器上、下密封筒过盈配合,导致井口连接坐封工具时需下压上部油管,常导致油管弯曲失稳,无法顺利下入坐封工具而推迟施工周期;即使强行下到位后,在逐个坐封隔离封隔器时,需要上、下反复提放坐封工具,密封经过长行程的摩擦而损坏,致使不能完成整个防砂作业,需要起出管柱更换密封重新下钻。这种更换费时费力,严重影响整个完井工艺进程。为此,研制了一种模块密封。该密封解决了以前施工作业中坐封工具下入困难及密封中途失效问题,保证了施工进度。
1 技术分析 1.1 施工工艺存在的问题工艺管柱由内、外管柱通过顶部封隔器连成一体,外管柱起分层隔离与悬挂筛管作用,内管柱实现封隔器坐封与验封功能,施工时只需1趟管柱作业即可把各层防砂筛管下到预定位置,并完成各个封隔器的坐封和验封。施工工艺存在如下问题:①将隔离封隔器与其坐封工具在井口连接过程中,由于坐封工具上的密封与封隔器密封筒过盈配合,需要油管承受较大的轴向力,此轴向力往往大于井场油管的临界载荷,下压油管时发生屈曲,导致坐封工具下入困难;②内管柱脱手,上、下移动坐封工具,密封在密封筒内长行程摩擦致使密封失效而无法承压坐封封隔器。
1.2 问题分析针对装有模块密封的坐封工具无法在井口下入问题,结合ø177.8 mm(7 in)多层简易防砂施工情况做如下假设,并建立工况计算模型,见图 1。

|
| 图 1 工况计算模型 Fig.1 Calculation model of working condition |
(1) 如图 1所示,隔离封隔器密封筒顶部与钻台大钩之间的距离(油管长度)为L,且视为单一等径油管。
(2) 视下端模块密封与密封筒过盈配合,为固定支撑,另一端为自由端。
将模型简化为一端固定、一端自由的欧拉梁模型,在轴向载荷及均布力作用下油管的屈曲临界载荷为[1-2]:
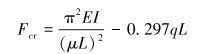
|
(1) |
式中:Fcr为屈曲临界载荷,kN;E、I、q、L分别为油管弹性模量(GPa)、惯性矩(m4)、均布载荷(kN/m)和长度(m);μ为约束条件。
用公式(1)计算得到在轴向载荷和均布力共同作用下油管的屈曲临界载荷与油管长度之间的关系,如图 2所示。从图可见,随着油管长度加长,屈曲临界载荷逐渐变小。当L=5 m时,Fcr=14.5 kN;当L=30 m时,ø73.0 mm油管在自重下发生屈曲,即油管无法直立。若要使6组模块密封顺利下入到位,则应满足下面条件之一:

|
| 图 2 屈曲载荷与油管长度的关系曲线 Fig.2 The relation of buckling load and tubing length |
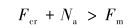
|
(2) |

|
(3) |
式中:Na为辅助下入力,kN;Fm为模块密封过盈配合产生的轴向摩擦力,kN。
考虑到式(2)中辅助下入力在平台上实现困难的情况,排除此条件,故式(3)是坐封工具可顺利下入的唯一可行条件。
2 关键零部件分析 2.1 结构设计根据上述分析结果设计模块密封结构,如图 3所示。该模块密封具有以下特点:①将4道矩形橡胶圈硫化粘接到金属环沟槽内,防止内管柱拖动过程中密封圈脱落;②在中间2道沟槽内预留退让槽,当橡胶受到径向压缩时,产生轴向伸缩,在密封筒内上、下滑动时保证矩形圈的收缩性,防止密封圈磨损;③模块密封在双向承压时,液体进入退让槽内挤压密封圈,具有自密封性能。

|
| 图 3 模块密封示意图 Fig.3 Block diagram of the module seal |
2.2 有限元分析 2.2.1 有限元模型建立
模块密封是坐封工具的一部分,工作时被安装在短节上,如图 4所示。表 1给出了模块密封的初始结构参数。

|
| 图 4 模块密封结构 Fig.4 The structure of the module seal 1—密封筒;2—金属环;3—矩形密封圈。 |
| 密封筒 内径 |
密封筒 外径 |
密封筒 长度 |
金属环 内径 |
金属环 外径 |
金属环 长度 |
矩形密封圈 外径 |
矩形密封圈 长度 |
矩形密封圈 宽度 |
退让槽 宽度 |
| 82.55 | 98.55 | 40.00 | 70.00 | 82.15 | 32.00 | 82.95 | 4.00 | 3.90 | 1.00 |
模块密封材料有2部分:密封部分采用HNBR材料,金属骨架采用2Cr13不锈钢材质,将橡胶通过硫化粘接在金属骨架沟槽侧面及底面,粘接强度大于橡胶的拉伸强度,以保证密封件在密封筒内壁上滑动时不致脱落。由于结构为轴对称结构,约束和介质压力也具有轴对称性,所以采用平面对称模型对其进行简化,采用具有塑性、大变形、超弹性及大应变能力的PLANE182单元进行分析[3]。橡胶邵氏硬度95,拉伸强度40 MPa,材料定义为超弹材料,采用Mooney-Rivlin模型,其常数C10=1.34,C01 =0.67[4-6],将2Cr13金属环处理成N80钢级材料,其弹性模量190 GPa,泊松比0.31,屈服强度552 MPa。考虑密封筒与矩形密封圈之间的接触面积较小,对接触部分进行局部细化,如图 5所示。将矩形密封圈外圆面设为接触面,密封筒内表面定义为目标面,设置多个接触对,接触单位为TARGE169,目标面CONTACT172。

|
| 图 5 有限元网格 Fig.5 The finite element mesh |
在预紧工况下,坐封工具带着多组模块密封进入固定密封筒内,由于过盈量的存在而产生一定的预应力;在工作过程中,模块密封在密封筒内部隔离上、下环空,其上、下承受一定的压差。
2.2.2 性能分析影响密封圈最大等效应力的主要因素是介质压力、密封圈的预压缩量和摩擦因数等。取摩擦因数为0.2、单边预压缩量为0.2 mm,通过对模块密封两侧面及与介质接触的表面施加不同载荷,分别得到模块密封外侧2道密封与外侧密封失效时内侧2道密封在不同压差下的应力分布云图,如图 6所示。

|
| 图 6 不同介质压力下模块密封的应力云图 Fig.6 Stress distribution of the module seal under different medium pressures |
从图 6可见,随着两侧介质压力的增大,密封圈发生较大的变形而被挤入密封间隙,挤入变形量随着介质压力的增大而变大。矩形密封圈的最大Von Mises应力发生在间隙处及与密封筒接触处,只有在介质压力35 MPa时,密封圈局部最大Von Mises应力为43.12 MPa,大于密封圈的拉伸强度,表层局部有可能被损坏;而介质压力小于35 MPa时,密封圈不会出现局部损坏情况。
衡量橡胶密封性能的关键参数是橡胶与金属之间的接触压力,一般要求接触压力大于密封压力才能满足密封要求[7]。不同介质压力下的接触应力云图如图 7所示。

|
| 图 7 不同介质压力下矩型密封圈的接触应力云图 Fig.7 The contact pressure of the rectangular seal ring under different medium pressures |
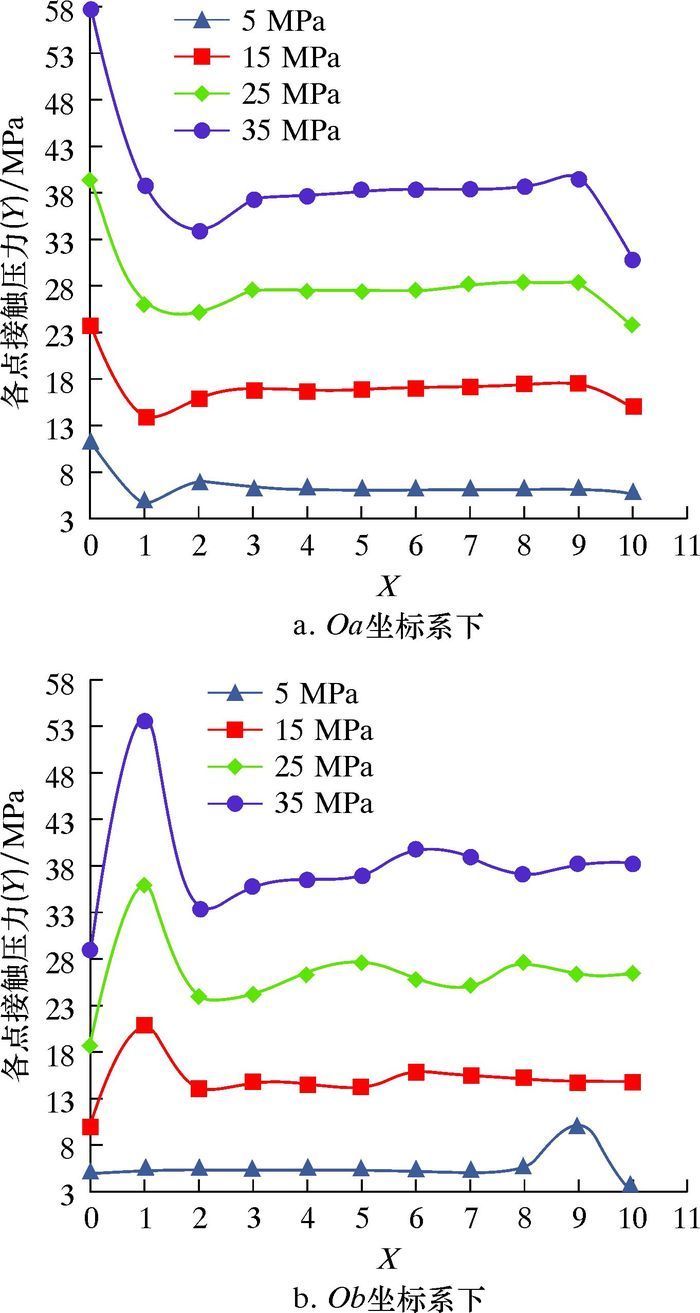
从图 7a可见,预压缩作用下,密封筒挤压矩形密封圈使其发生变形,提供接触压力来起密封作用。由于矩形密封圈的底面与侧面被粘接在金属环上,限制了矩形密封圈的轴向位移,所以会在侧面粘接处出现接触压力峰值,如图 7b至图 7d所示。随着两边介质压力的增大,矩形密封圈变形量增大并逐渐被压实以提供越来越大的接触压力,保证密封性能。提取内、外密封上侧矩形密封圈接触面上各点接触压力,绘制不同坐标系下接触压力分布,结果如图 8所示。从图可见,在不同压差下,接触面上的接触压力峰值均出现在粘接处,远离粘接处接触压力逐渐平稳,平稳段均值高出相应压差2~3 MPa,可满足不同压差下的密封要求。
|
| 图 8 不同压力下内、外密封上侧接触压力分布 Fig.8 Distribution of contact pressure on the upper side of inner and outer seals at different pressures |
3 试验研究 3.1 试验内容
为解决现场出现的问题,将3个模块密封装入设计工装内进行试验,具体试验内容为:①往复推拉试验,往复行程共80 m,测试摩擦力;②常温条件下,通过4个压力台阶(8、14、21和35 MPa)进行密封试验。
3.2 试验结果分析80 m往复推拉试验中,分别在20、40、60和80 m结束时测量各自最大静摩擦力,其值分别为9.32,8.43,8.32和8.38 kN。各行程后密封效果见图 9。

|
| 图 9 各行程后密封效果 Fig.9 The sealing performance after the strokes |
由试验结果可知,随着往复推拉行程的增加,3个模块密封的最大静摩擦力逐渐减小,最小为8.32 kN,即6个模块密封的最大静摩擦力Fm=16.64 kN。现场施工时,当模块密封ø73.0 mm NU油管长度L=5 m时,允许下压载荷Fcr=14.50 kN,这与模块密封过盈配合产生的摩擦力Fm=16.64 kN相差不大,误差在13%之内,即0.2 mm的过盈量较为合适。从图 9可见,经过各行程后的密封压力仍能密封35 MPa压差,经过80 m行程磨损后,仍具有坐封隔离封隔器的能力。
4 结论(1) 模块密封退让槽的设计使得在一定油管长度下,井口可顺利下入坐封工具,保证了施工进程。
(2) 4道矩形密封圈的粘接结构可以解决模块密封在密封筒内反复拖动磨损而导致密封失效的问题。
(3) 在多层简易及一次多层的防砂施工工艺中,多组模块密封在坐封工具上的使用可保证多个封隔器的成功坐封,避免了服务工具起钻、更换模块密封和再下钻的问题,节省了时间,减轻了工人的劳动强度。
| [1] | 刘鸿文. 材料力学[M]. 4版.北京: 高等教育出版社, 2004, 280-300. LIU H W. Mechanics of materials[M]. Fourth Edition. Beijing: Higher Education Press, 2004, 280-300. |
| [2] | 铁摩辛柯S P, 盖莱J M. 弹性稳定理论[M]. 2版. 张福范, 译. 北京: 科学出版社, 1965: 100-120. TIMOSHENKO S P, GERE J M. Theory of elastic stability[M]. 2nd ed. ZHANG F F, trans. Beijing:Science Press, 1965:100-120. |
| [3] | 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003, 666-676. WANG X C. Finite element method[M]. Beijing: Tsinghua University Press, 2003, 666-676. |
| [4] | 钱文强, 蒋国璋, 谢良喜, 等. 矩形密封圈应力和接触压力的影响因素[J]. 液压与气动, 2015(3): 32-35. QIAN W Q, JIANG G Z, XIE L X, et al. Influencing factors of stress and contact pressure in rectangular seal[J]. Chinese Hydraulics & Pneumatics, 2015(3): 32-35. |
| [5] | 谭晶, 杨卫民, 丁玉梅, 等. 矩形橡胶密封圈的有限元分析[J]. 润滑与密封, 2007, 32(2): 36-39. TAN J, YANG W M, DING Y M, et al. Finite element analysis of rectangular rubber seals[J]. Lubrication Engineering, 2007, 32(2): 36-39. |
| [6] | 吴话怡, 周思柱, 李宁, 等. 超高压管道自增强处理密封有限元分析[J]. 石油机械, 2017, 45(3): 118-121. WU H Y, ZHOU S Z, LI N, et al. Finite element analysis of sealing for self-reinforced process of ultra-high pressure pipeline[J]. China Petroleum Machinery, 2017, 45(3): 118-121. |
| [7] | 曹为, 刘军, 王宇臣, 等. 特殊密封面O形圈非标密封槽结构研究[J]. 石油机械, 2016, 44(1): 55-58. CAO W, LIU J, WANG Y C, et al. Study on non-standard O-ring seal groove in special seal surface[J]. China Petroleum Machinery, 2016, 44(1): 55-58. |


