0 引言
水力喷砂射孔器上的喷嘴是射孔过程中实现能量转换,获得高速喷砂射流的核心元件,同时也是冲蚀磨损最严重的元件[1-4]。因此,针对喷嘴性能的研究对水力喷砂射孔器效率和使用寿命具有重要意义[5]。现阶段的研究方法主要有2种:数值模拟和室内试验[6-7]。梁钦等[8]利用数值模拟对锥直形喷嘴和流线形喷嘴内的流场压力进行了对比,认为维多辛斯基曲线喷嘴能量损失最小;徐艳等[9]利用数值模拟对不同内流道形状喷嘴内流场的等速核进行对比分析,认为等变速形喷嘴射孔效果最好;熊青山等[10]通过室内试验测试了不同结构喷嘴的流量系数,认为流线形喷嘴的流量系数最大,锥直形喷嘴流量系数最小。
多数学者利用数值模拟方法研究时,使用的模型来流方向垂直于喷嘴入口截面,忽略了射孔器喷嘴入流的实际情况。采用室内试验方法时,进行的多是清水试验,未考虑磨料颗粒对喷嘴的冲蚀。为此,笔者借助FLUENT软件,运用离散相模型,从射流特性和冲蚀磨损2方面综合分析,对综合性能最佳的喷嘴结构进行了优选。所得结论对喷嘴结构优化具有一定的指导意义。
1 锥直形喷嘴能量损失原因分析 1.1 喷嘴中液相能量损失根据工程流体力学可知,局部水头损失是造成喷嘴射流能量损失的主要原因[10-12]。局部水头损失是指由于水流边界发生不连续突然改变,导致水流在惯性作用下与壁面脱离而产生的能量损失[13]。目前,尚没有全面的理论计算公式,通常采用一个流速水头与一个局部水头损失系数的乘积来表示[14],即:
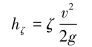
|
(1) |
式中:hζ为局部水头损失,ζ为局部水头损失系数,v为流速,g为重力加速度。
射孔器中流体进入喷嘴时存在2处局部结构突变:一处在喷嘴入口处,一处在圆锥段与圆柱段连接处。因此,传统锥直形喷嘴的能量损失主要由2部分组成。查局部水头损失系数表可知,对于断面突然缩小的结构,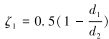
令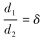
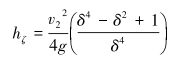
|
(2) |
式中:v2为喷嘴入口速度。
由公式(2)可知,δ的取值决定了喷嘴局部水头损失hζ的大小,而δ的大小由d1(即喷嘴收缩段出口直径)和d2的比值确定。因此可以认为,喷嘴局部水头损失主要取决于入口收缩段的形状尺寸。
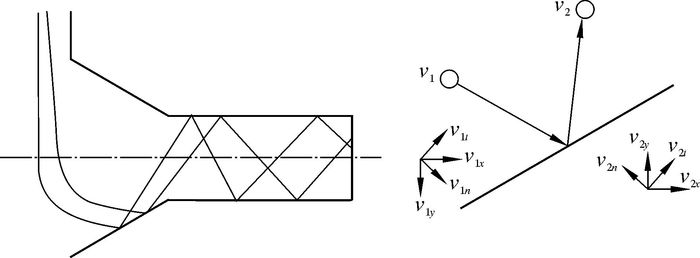
1.2 喷嘴中固相颗粒能量损失磨料粒子进入喷嘴的过程中,由于运动方向的改变会与喷嘴内壁发生碰撞;若粒子入射速度足够大,则会与喷嘴内壁发生多次碰撞,如图 1所示。
|
| 图 1 固体颗粒与喷嘴内壁的碰撞 Fig.1 Solid particles collision with the inner wall of the nozzle |
固体颗粒与壁面的碰撞不属于完全弹性碰撞,碰撞过程中存在能量损失。因此,碰撞后的粒子运动速度v2必定小于碰撞前粒子的速度v1。碰撞次数越多,粒子能量损耗越大,喷嘴内壁的冲蚀磨损越严重。
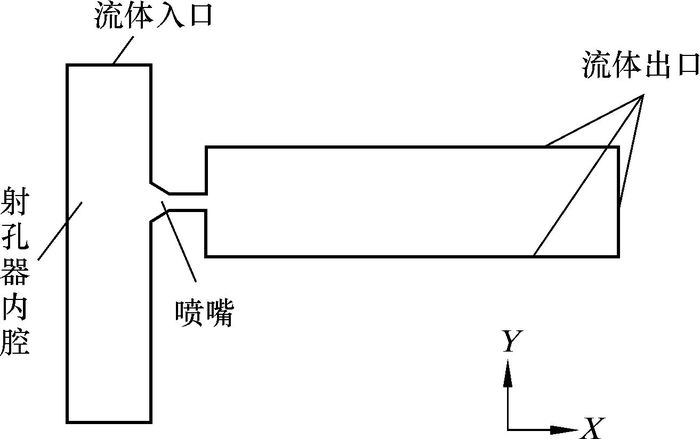
1.3 锥直形喷嘴仿真分析由于喷嘴射流性能难以直接观测,笔者借助流体分析软件FLUENT建立如图 2所示的喷嘴物理模型,对射孔器喷嘴的射流特性进行分析。选用标准k-ε湍流模型和离散相模型(DPM)对整个固液两相流场进行模拟仿真,采用SIMPLE算法进行求解计算。
|
| 图 2 喷嘴物理模型 Fig.2 Nozzle model |
分析过程中,各喷嘴模型均采用相同的边界条件:①速度入口。流体相速度为11 m/s,湍流参数设置为湍流强度5%,水力直径30 mm;在injection中设置固体颗粒速度为10 m/s,直径为0.5 mm,质量流量0.02 kg/s。②压力出口。流体从喷嘴喷出后在大气压下做自由射流,因此压力设置为0.1 MPa;湍流参数设置为湍流强度8%,水力直径40 mm。③边界设置。物理模型中除入口和出口,其余边界均设置为reflect壁面。根据上述设置进行模拟仿真。图 2为喷嘴的物理模型图。
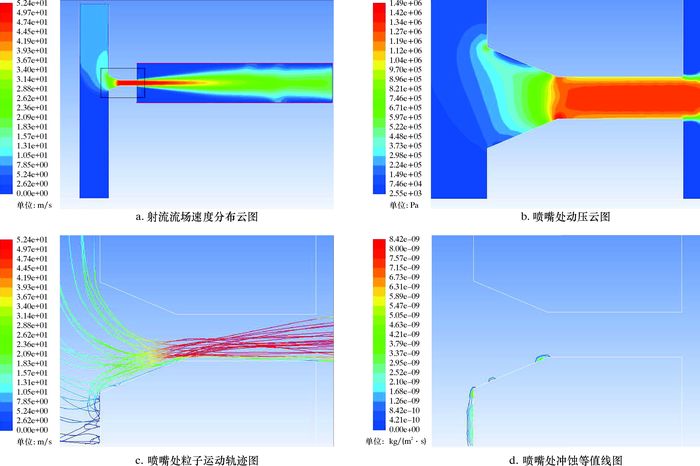
由模拟结果可以明显看出:①射孔器喷嘴来流方向并非垂直进入,而这种进入方式会导致喷嘴入口上、下两端存在压差和速度差;且流场速度和压力的变化主要发生在喷嘴入口收缩段内,如图 3a和图 3b所示;②液固两相在喷嘴入口处均存在脱离喷嘴上壁面的现象,如图 3a和图 3c所示;③固体颗粒运动过程中会与喷嘴内壁发生碰撞,造成颗粒速度降低、喷嘴内壁冲蚀损伤,如图 3c和图 3d所示。因此,可以认为喷嘴入口收缩段结构对其射流特性具有重要影响。
|
| 图 3 锥直形喷嘴射流流场仿真结果组图 Fig.3 Simulationresultsofthecone straight nozzle jet flow field |
2 射孔器喷嘴入口收缩段结构设计
由上述理论分析和数值仿真可知,改善锥直形喷嘴射流性能的关键在于优化入口收缩段结构。因此,笔者针对喷嘴入口收缩段结构,进行以下5种设计:
(1) 圆弧入口锥直形喷嘴,其内流道以锥直形喷嘴为基础,在入口处设置有一端圆弧(类似倒圆角)。
(2) 椭圆形喷嘴,入口段流道母线为椭圆曲线的一部分;出口段设置为圆柱段。则根据椭圆方程有:
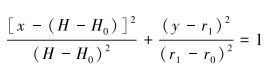
|
(3) |
式中:H为喷嘴总长度,H0为喷嘴出口圆柱段长度,r1为喷嘴收缩段入口半径,r0为喷嘴收缩段出口半径。
(3) 等变速形喷嘴,入口段流道母线是一条等变速曲线,出口段流道是直圆柱形。该喷嘴特点为入口曲线段内流体速度变化率为常数,由此可以得到等变速曲线方程为[15]:
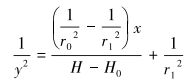
|
(4) |
(4) 基于维多辛斯基曲线的收缩喷嘴,该喷嘴内流道入口收缩段母线为维多辛斯基曲线的一部分。根据维多辛斯基公式有[16-17]:
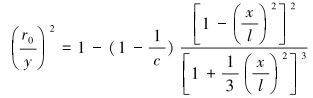
|
(5) |
式中:c为收缩比,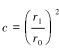
(5) 流线型喷嘴,其内流道母线为流线形。根据流线方程有[4]:
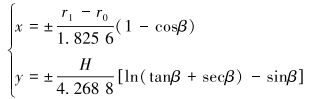
|
(6) |
式中:β为流道角,取值范围为0°~85°。
曲线上半段取公式(6)的正值,曲线下半段取公式(6)的负值。
3 仿真结果及对比分析为了对比分析上述新型喷嘴与传统锥直形喷嘴的射流性能,以图 2中喷嘴物理模型为基础,将锥直形喷嘴依次换成上述5种新型喷嘴,设置相同的湍流模型、离散相模型、边界条件以及算法,利用FLUENT软件进行数值模拟,并进行仿真结果对比分析。
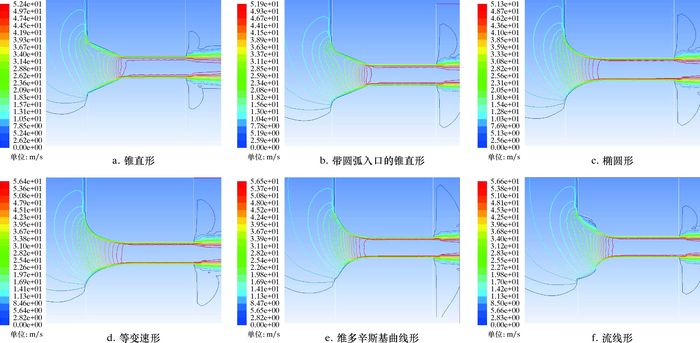
3.1 喷嘴内速度分布图 4为喷嘴内速度等值线分布图。由图可以看出,射孔器上喷嘴入口来流速度等值线呈不均匀的“扇形”分布,喷嘴入口上下端存在明显的速度差;喷嘴内速度变化主要集中在入口收缩段内;相同条件下,等变速形喷嘴和椭圆形喷嘴内流体得到了充分发展,流线形喷嘴、维多辛斯基曲线形喷嘴和锥直形喷嘴入口处都形成了不同程度的涡流,带圆弧入口的锥直形喷嘴内流体在收缩段与圆柱段连接处并未充分发展。
|
| 图 4 喷嘴内速度等值线分布图 Fig.4 Velocity contour distributionin the nozzle |
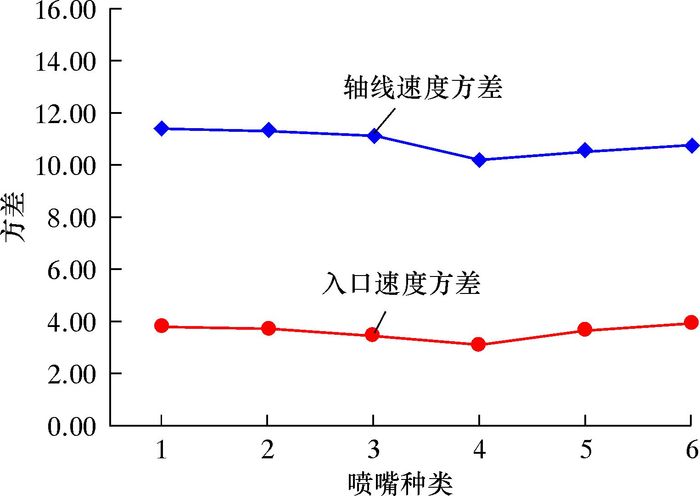
水力喷砂射孔过程中,相同射孔间距下,冲击靶件的射流速度越大,则射孔效果越好;而对于喷嘴,入口处速度差越大,则上、下端壁面冲蚀腐蚀速率差越大,使喷嘴截面不能继续保持圆形,影响其流量系数。因此,借助方差公式[14],对比相同射流间距下,上述6种喷嘴射流轴线速度和入口速度的离散程度,绘制成折线图,结果如图 5所示。
|
| 图 5 速度方差 Fig.5 Velocity variance |
从图 5可知,维多辛斯基曲线形喷嘴和流线形喷嘴轴线速度方差最大,其次为带圆弧入口的锥直形喷嘴和传统锥直形喷嘴,而椭圆形喷嘴和等变速形喷嘴轴线速度方差最小。等变速形喷嘴入口速度差最小,流线形喷嘴入口速度差最大。
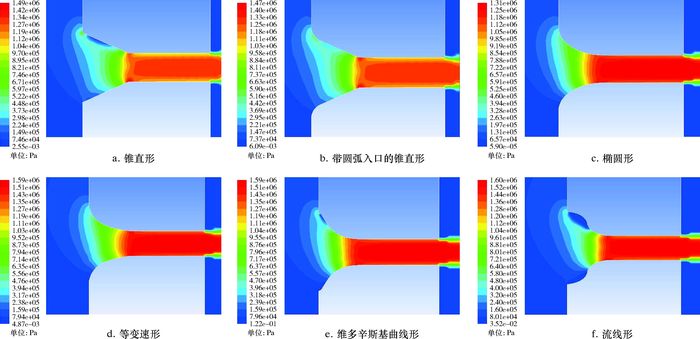
3.2 喷嘴内压力分布图 6为喷嘴内压力分布。从图中6种喷嘴内压力分布云图可以看出,喷嘴内的压力变化主要发生在入口收缩段;在相同的来流条件下,曲线形喷嘴射流动压要高于锥直形喷嘴;锥直形喷嘴、带圆弧入口的锥直形喷嘴、维多辛斯基曲线形喷嘴和流线形喷嘴内均存在不同程度的低压区,椭圆形喷嘴和等变速形喷嘴内则不存在低压区,但后者的压力分布更加平稳。
|
| 图 6 喷嘴内动压分布图 Fig.6 Dynamic pressure distribution in the nozzle |
综上所述,在相同数值模拟条件下,等变速形喷嘴入口速度差最小,轴线速度衰减最慢,收缩段内压力分布最均匀,综合性能最优。
4 等变速形喷嘴结构优化等变速形喷嘴的几何尺寸包括出口直径d0、入口直径d1、圆柱段长度l0和收缩段长度l1。其中喷嘴出口直径通常由施工排量和泵压决定[18],目前现场施工中使用的喷嘴出口直径多为6 mm。
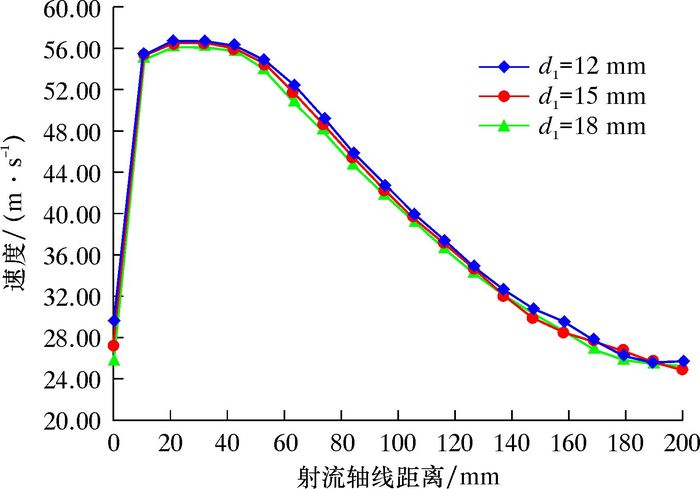
4.1 入口直径对射流性能的影响在其他参数不变的情况下,仅改变喷嘴入口直径d1的取值进行数值模拟,结果如图 7所示。从图可以看出,入口直径变化对喷嘴射流轴线速度变化影响不大。
|
| 图 7 不同入口直径下等变速形喷嘴射流轴线速度分布 Fig.7 Axis velocity distribution of equal speed change nozzle under different inlet diameters |
图 8为不同入口直径下等变速形喷嘴内壁冲蚀速率等值线分布图。由图可以看出,尽管入口直径12 mm时,喷嘴入口处磨料粒子冲蚀分布较多,但其最大冲蚀速率为1.68×10-8 kg/(m2·s),明显低于入口直径为15和18 mm的喷嘴。
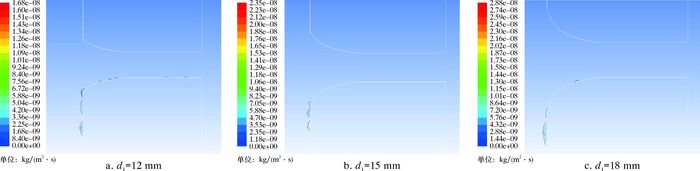
|
| 图 8 不同入口直径下等变速形喷嘴内壁冲蚀速率等值线分布 Fig.8 Distribution of erosion rate contour on the inner wall of equal speed change nozzle under different inlet diameters |
4.2 圆柱段长度对射流特性的影响
喷嘴尺寸中圆柱段长度与出口直径的比值,称为长径比。在其他尺寸参数不变的条件下,分别取长径比为1、2和3(即圆柱段长度l0分别为6、12和18 mm),分析不同长径比下等变速形喷嘴的射流特性,仿真结果如图 9和图 10所示。
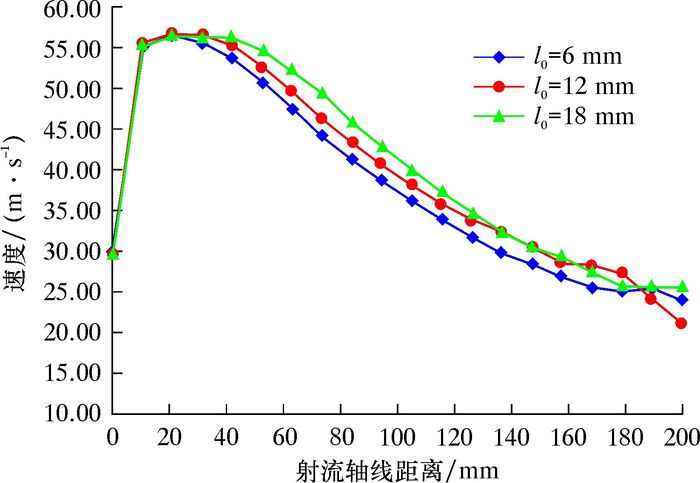
|
| 图 9 不同圆柱段长度下等变速形喷嘴射流轴线速度分布 Fig.9 Axis velocity distribution of equal speed change nozzle under different cylindrical section lengths |

|
| 图 10 不同圆柱段长度下等变速形喷嘴内壁冲蚀速率等值线分布 Fig.10 Distribution of erosion rate contour on the inner wall of equal speed change nozzle under different cylindrical section lengths |
由图 9可知,虽然圆柱段长度几乎不影响喷嘴射流速度大小,但圆柱段长度越长,喷嘴射流的等速核长度越长。由图 10可以看出,圆柱段长度为6 mm时,磨料粒子对喷嘴内壁的冲蚀速率最小,其次是圆柱段长度18 mm的喷嘴,圆柱段长度为12 mm的喷嘴内壁冲蚀速率最大。
4.3 收缩段长度对射流特性的影响喷嘴收缩段长度l1变化,则等变速曲线的线型发生变化。现对l1分别为5、10和15 mm的3种等变速形喷嘴进行数值模拟,分析其在来流相同时的射流特性,结果如图 11和图 12所示。
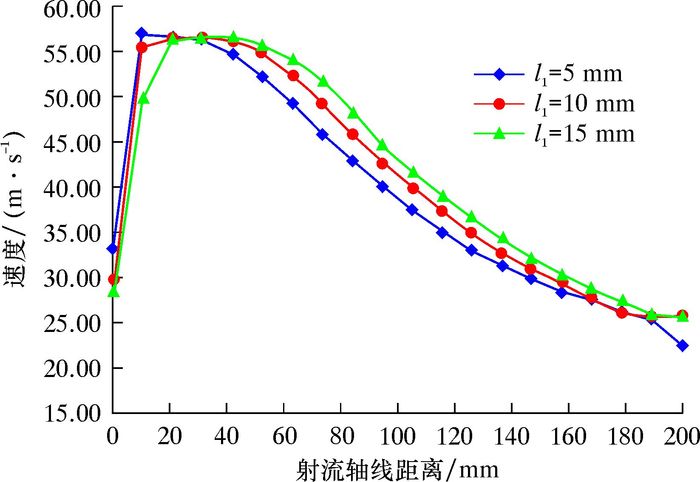
|
| 图 11 不同收缩段长度下等变速形喷嘴射流轴线速度分布 Fig.11 Axis velocity distribution of equal speed change nozzle under different contraction section lengths |
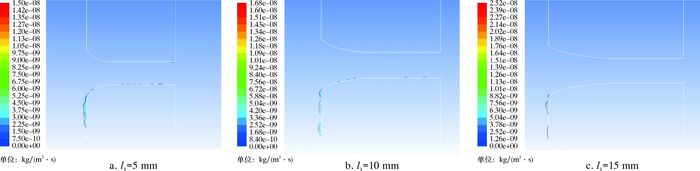
|
| 图 12 不同收缩段长度下等变速形喷嘴内壁冲蚀速率等值线分布 Fig.12 Distribution of erosion rate contour on the inner wall of equal speed change nozzle under different contraction section lengths |
由图 11可知,收缩段为5 mm的喷嘴对射流的加速作用最快,且最大射流速度为57.11 m/s,但射流的等速核长度明显较短,而收缩段为15 mm的喷嘴对射流的加速作用最慢。因此,相对而言,收缩段长度为10 mm的喷嘴射流性能更好。由图 12可以看出,3种喷嘴受到的冲蚀速率分别为1.50×10-8、1.68×10-8和2.52×10-8 kg/(m2·s);而根据冲蚀分布情况来看,第3种喷嘴内壁冲蚀区域较少,其次是第2种喷嘴,内壁冲蚀区域最多的是第1种喷嘴。
综上所述,在出口直径6 mm时,优选等变速形喷嘴的结构参数为:入口直径为12 mm,圆柱段长度18 mm,收缩段长度10 mm。
5 结论(1) 水力喷砂射孔器喷嘴射流能量损失主要由入口收缩段处的局部水头损失和磨料颗粒碰撞喷嘴壁面引起。
(2) 等变速形喷嘴入口速度差最小,轴线速度衰减最慢,收缩段内压力分布最均匀,综合性能最优。
(3) 综合射流特性和喷嘴冲蚀考虑,等变速形喷嘴的最佳结构参数为:出口直径6 mm,入口直径12 mm,圆柱段长度18 mm,收缩段长度10 mm。
| [1] | 王治国, 冉亚楠, 隆世明, 等. 水力喷射工具射孔过程液固两相流冲蚀数值模拟[J]. 石油机械, 2015, 43(9): 61–65. |
| [2] | STOCKHAUSEN H W, GARCIA SANCHEZ D G, LUONGO S, et al.In-depth evaluation of deep-rock hydrajet results shows unique jetted rock surface characteristics[R]. SPE 153333, 2012. |
| [3] | SURJAATMADJA J B, BEZANSON J, LINDSAY S D, et al.New hydra-jet tool demonstrates improved life for perforating and fracturing applications[R]. SPE 113722, 2008. |
| [4] | 韩继勇, 逄仁德, 王书宝, 等. 水力喷射环空压裂技术在长庆油田的应用[J]. 钻采工艺, 2015, 38(1): 48–50. |
| [5] | 艾娟, 张海, 李鹏勃, 等. 水力喷射分段压裂技术在靖边油田水平井中的应用[J]. 延安大学学报(自然科学版), 2015, 34(3): 85–88. |
| [6] | 汤积仁, 卢义玉, 欧阳梦迪, 等. 水力喷射压裂新型喷嘴设计优化及性能评价[J]. 中国石油大学学报(自然科学版), 2015, 39(1): 72–78. |
| [7] | ANIRBAN G, RONALD M, RAM B. Numerical simulation of high-speed turbulent water jets in air[J]. Journal of Hydraulic Research, 2010, 48(1): 119–124. DOI: 10.1080/00221680903568667 |
| [8] | 梁钦, 高贵军, 刘邱祖. 基于CFD的喷嘴轮廓对喷嘴能量损失影响分析[J]. 矿山机械, 2014, 42(3): 94–98. |
| [9] | 徐艳, 李青燕. 不同流道形状的水力射孔喷嘴数值模拟[J]. 中国城市经济, 2014, 9(20): 155. |
| [10] | 熊青山, 李佳, 安传奇, 等. 射流元件平面喷嘴结构优化试验研究[J]. 凿岩机械气动工具, 2010, 3(3): 39–43. |
| [11] | 袁恩熙. 工程流体力学[M]. 北京: 石油工业出版社, 2013: 87-88. |
| [12] | 贾月梅. 流体力学[M]. 北京: 国防工业出版社, 2006: 183-193. |
| [13] | 张泌. 圆管突然扩大与突然缩小的局部水头损失系数的研究[J]. 科学技术与工程, 2014, 14(28): 139–162. |
| [14] | 陈朝. 常见管道局部水头损失的数值模拟[D]. 天津: 天津大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10056-2009071354.htm |
| [15] | 汪崎生. 用数值网格变换法求解等变速喷嘴的有势流场[J]. 江汉石油学院学报, 1989, 11(3): 60–71. |
| [16] | 李敏霞, 李秀辉, 陈佩寒. 一种实用的维多辛斯基曲线风洞收缩段展开方法研究[J]. 应用能源技术, 2010(8): 1–4. |
| [17] | 何枫, 谢峻石, 杨京龙. 喷嘴内部流道型线对射流流场的影响[J]. 应用力学学报, 2001, 18(4): 114–119. |
| [18] | 谢刚儒. 连续油管水力喷砂射孔工艺研究[D]. 成都: 西南石油大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015599077.htm |




