2. 中国核动力研究设计院;
3. 中国石油塔里木油田分公司
2. Nuclear Power Institute of China;
3. PetroChina Tarim Oilfield Company
0 引言
塔里木油田有往复压缩机200余台,其中进口往复压缩机所占比例较大,其零配件多半由生产厂家原装提供。近年来,随着生产成本的不断升高,油田加快了设备零配件的国产化进程,与国内相关制造厂商合作测绘并生产了往复压缩机的重要部件——活塞。为了分析和评价国产活塞的工作性能与振动指标,笔者首先对国产化压缩机活塞组件进行模态分析[1],然后结合缸套振动信号响应谱和振动特性来评估塔里木油田往复压缩机活塞国产化的合理性。
1 国产活塞的改造过程塔里木油田某作业区的DTY185ML13*8型往复压缩机为双缸双作用式,压缩介质为石油伴生天然气,高压下易液化,对活塞和缸体造成腐蚀。该往复压缩机采用交流电机驱动,额定功率185 kW,额定转速990 r/min,进气压力0.15~0.30 MPa,排气压力2.00 MPa。该机组于2007年12月投入使用。2010年和2013年对3台伴生气压缩机大修过程中均发现一级活塞活塞环与支撑环槽磨损严重。其中,自投运至第1次大修期间,同型号的3台伴生气压缩机累计运行时间均在2万h左右,短于预定周期3万h。
鉴于活塞的大修周期短以及对原装活塞采购费用的升高,油田设备管理部门首先尝试对原装一级活塞进行仿造,以延长其使用寿命并提高整个机组运行时率及安全性,评估其合理性和适用性后再做推广。
对该往复压缩机的一级活塞材质进行了化验分析。在改造活塞的选材上既要匹配或优于原装活塞材质的性能,但又不能优于气缸体的材质要求,以免出现拉缸现象时气缸的损伤过大。根据原装活塞材质的化学成分,查询机械材料手册,发现一种LY12的材料,该材料的金属元素质量分数与原活塞材质成分一致,且强度相近,选用的仿造活塞材质LY12化学元素与原装活塞件元素基本一致,可以作为活塞材质的选择。LY12是一种高强度硬铝,耐热性可达150 ℃,满足压缩气体时的温度要求(伴生天然气被压缩后温度最高为120 ℃);屈服强度685 MPa,符合抗拉强度≥425 MPa的要求[2]。
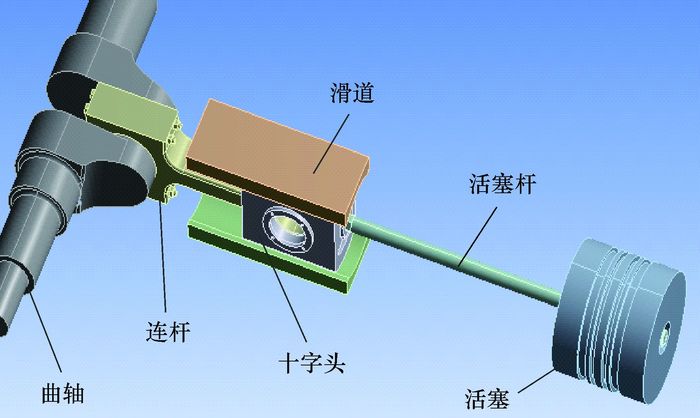
2 模态分析通过对往复压缩机曲轴、连杆、十字头、活塞杆及活塞进行测绘,其中,活塞结构的主要参数如表 1所示。按照测绘尺寸使用Pro/E软件建模,模型如图 1所示。
| 位置 | 标准尺寸 |
| 活塞外径 | 326.11~326.15 |
| 活塞长度 | 276.00~276.30 |
| 支撑环槽宽度 | 25.40~25.46 |
| 支撑环槽底径 | 306.80~306.85 |
| 活塞环槽宽度 | 12.70~12.76 |
| 活塞环槽底径 | 300.88~300.93 |
| 活塞杆外径 | 38.08~38.10 |
| 活塞杆总长 | 1 005.50~1 006.50 |
|
| 图 1 往复压缩机模型 Fig.1 The reciprocating compressor model |
2.1 理论基础
振动模态可以预测出机械结构在此频段受到外部或内部各种振源作用下产生的实际振动响应,是机械结构动态设计及机械设备状态监测与故障诊断的重要方法[3]。
在往复压缩机活塞振动模态分析中,活塞组件的固有频率和模态振型是其固有特性,与其结构的质量和刚度分布有关。分析活塞组件的固有频率和模态振型之间的关系有助于对活塞结构和材质进行改进。为此,建立压缩机活塞振动方程。
微分方程如下:
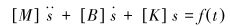
|
(1) |
式中:[M]为质量矩阵,[K]为刚度矩阵,s为位移向量,[B]为阻尼矩阵,f[t]为外部激励矩阵。
振动模态是活塞的一种固有特性,在活塞的模态分析时不能施加非零位移约束,因此,方程中的阻尼[B]和外部载荷f[t]可忽略。
对该微分方程求解,假设该活塞以固有频率振动,将s=øsin(ωt+φ)代入式(1)可得:
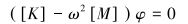
|
(2) |
令其特征方程
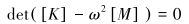
|
(3) |
则所求得的{ω}即为活塞振动的固有频率,特征向量{ø}即为ω所对应的振型。
2.2 模态计算往复压缩机工作过程中,吸排气过程具有交替性和周期性,另外活塞压缩气体时的速度也具有时变性,因此会对压缩气体引起压力脉动,活塞也必受到该脉冲的影响而引起振动。当往复压缩机活塞的固有频率接近压缩机的激发主频率时,就会使压缩机活塞及其机组处于共振状态,甚至引起压缩机基础和管系的强烈振动[1]。
1阶激发频域也称主激发频率。激发频率的计算方法如下:
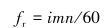
|
(4) |
式中:i为激发频率fr的阶次,i=1, 2, ……;m为曲轴转1周吸气或排气的次数,单作用往复压缩机m=1,双作用往复压缩机m=2;n为往复压缩机主轴的转速,r/min。
由于活塞杆的曲轴连杆和十字头距离活塞位置较远,笔者只研究活塞与活塞杆组成系统的模态及其响应谱的分析。该伴生气往复压缩机一级活塞组件各结构的材料特性如表 2所示。
| 名称 | 材料 | 密度/(kg·m-3) | 弹性模量/GPa | 泊松比 |
| 活塞 | LY12 | 2 850 | 74.2 | 0.36 |
| 活塞杆 | 40Cr | 7 830 | 207.0 | 0.28 |
| 螺母 | Q345 | 7 890 | 206.0 | 0.28 |
活塞组件的工作状态为无变形承压模式,材料性质为线性且各向同性,工作环境温度为恒温80 ℃,提取模态参数设置阶数为6阶,最后对该模态进行求解计算[1]。
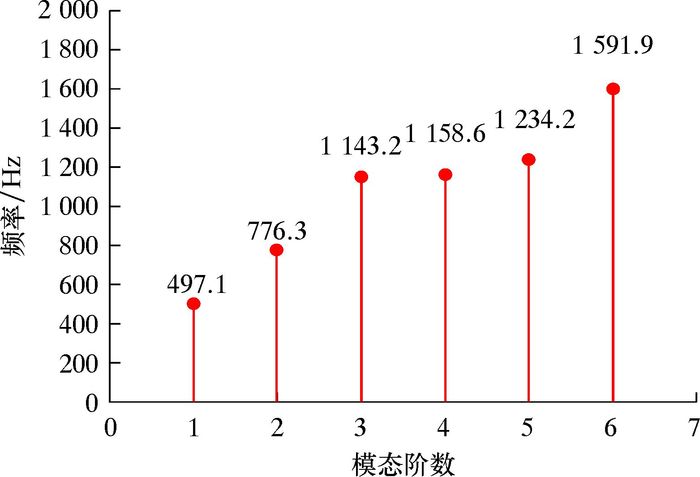
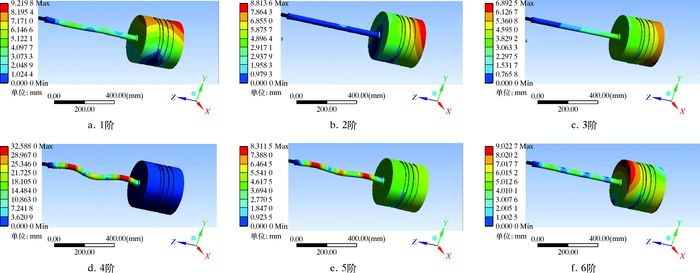
求解活塞组件工作状态下的6阶固有频率和模态振型,6阶固有频率和应力场分布如图 2和图 3所示。由图可以看出,该材料活塞组件的6阶模态振型明显,表明如果该往复压缩机工作时产生的激振频率一旦与活塞的固有频率相等,必然发生共振,该往复压缩机主轴转速为990 r/min时,激发主频率为33.0 Hz,远远小于活塞受到活塞杆拉压作用下的1阶共振频率497.1 Hz,因此活塞在往复运动过程中,不会发生共振,运行可靠[4]。
|
| 图 2 活塞组件的模态阶数 Fig.2 Modal order of the piston assembly |
|
| 图 3 6阶模态振型 Fig.3 The six order modal vibration type |
3 响应谱分析
响应谱分析又称冲击谱分析,用于确定机械结构在受到含有特定频谱成分的振动激励时所产生的稳态响应,也是预测受到外部激励(强迫振动)的结构峰值响应的分析方法。取代耗时的时域瞬态分析,可以采用响应谱分析快速地近似分析结构的峰值响应(如动应力等)[1, 5]。
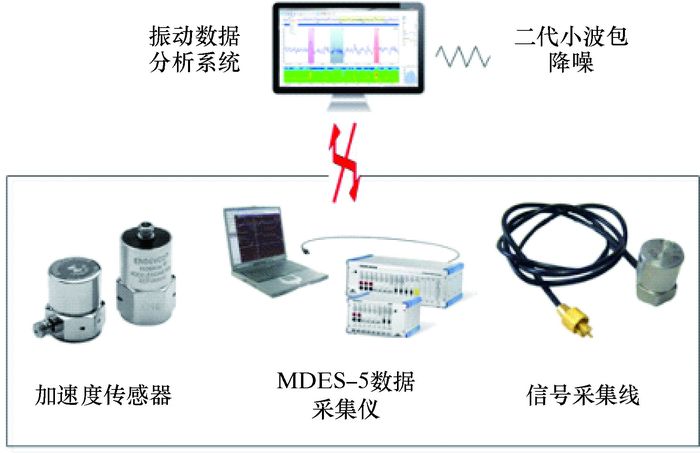
该往复压缩机一级活塞国产化改造后,采用中国石油大学(北京)故障诊断实验室自主研发的数据采集仪MDES-5型故障诊断系统,采集及分析系统如图 4所示。现场采集数据,将加速度传感器吸附在一级压缩缸的缸套表面,采集仪的采样频率为16 kHz,采样点数为4 096。
|
| 图 4 振动信号的采集及分析系统 Fig.4 Vibration signal acquisition and analysis system |
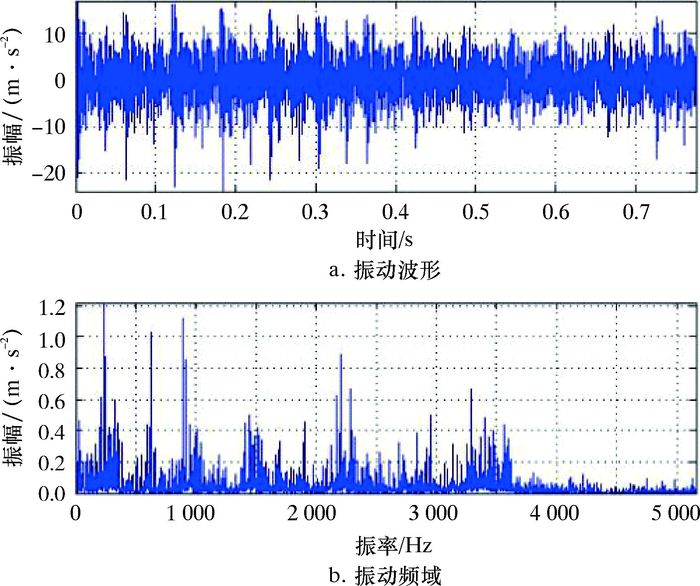
通过对该压缩机缸套的振动监测数据时频域分析,鉴于现场采集振动数据的噪声水平较高,振动信号容易被噪声淹没,经过二代小波包降噪[6],得出活塞缸套振动的频谱及幅值,如图 5所示。振动信号加速度谱如表 3所示。缸套的振动频谱均避开了活塞组件的固有频率,因此,国产化后活塞工作时不会出现共振现象,也表明活塞的材质选择和结构设计符合要求。
|
| 图 5 缸套的振动信号 Fig.5 Cylinder vibration signal |
| 频率/Hz | 幅值/
(m·s-2) |
| 33.54 | 4.5 |
| 65.79 | 2.0 |
| 99.33 | 2.5 |
| 116.10 | 2.0 |
| 132.87 | 2.4 |
| 166.41 | 3.1 |
| 198.66 | 4.1 |
| 199.95 | 3.5 |
| 215.43 | 6.0 |
| 216.72 | 2.6 |
| 232.20 | 12.0 |
| 233.49 | 2.5 |
| 248.97 | 8.5 |
| 265.74 | 3.6 |
| 282.51 | 4.1 |
| 297.99 | 2.0 |
| 299.28 | 3.7 |
| 314.76 | 3.9 |
| 316.05 | 4.0 |
| 331.53 | 5.9 |
| 332.82 | 3.9 |
| 348.30 | 4.4 |
| 365.07 | 3.4 |
| 381.84 | 3.2 |
| 514.71 | 2.2 |
| 548.25 | 2.4 |
| 597.27 | 4.3 |
| 614.04 | 4.1 |
| 630.81 | 10.1 |
| 664.35 | 2.8 |
| 797.22 | 2.1 |
| 863.01 | 2.0 |
| 879.79 | 2.2 |
| 895.27 | 2.0 |
| 896.56 | 11.0 |
| 912.04 | 3.9 |
| 913.33 | 8.3 |
| 914.62 | 2.7 |
| 945.58 | 4.3 |
| 946.87 | 3.8 |
| 948.16 | 2.0 |
| 962.35 | 2.4 |
| 979.12 | 2.8 |
| 995.89 | 3.6 |
| 1 012.66 | 4.1 |
| 1 046.20 | 3.2 |
| 1 061.68 | 2.0 |
| 1 194.55 | 2.0 |
| 1 195.84 | 2.4 |
| 1 394.50 | 2.6 |
| 1 411.27 | 4.4 |
| 1 444.81 | 4.9 |
| 1 446.10 | 2.1 |
| 1 460.29 | 3.8 |
| 1 461.58 | 3.5 |
| 1 462.87 | 2.5 |
| 1 477.06 | 3.0 |
| 1 478.35 | 2.6 |
| 1 493.83 | 3.6 |
| 1 510.60 | 4.1 |
| 1 527.37 | 3.6 |
| 1 544.14 | 3.4 |
| 1 660.24 | 2.4 |
| 1 693.78 | 3.3 |
| 1 892.44 | 3.2 |
| 1 909.21 | 4.5 |
| 2 092.39 | 2.1 |
| 2 124.64 | 3.0 |
| 2 125.93 | 2.1 |
| 2 174.95 | 6.1 |
| 2 191.72 | 3.7 |
| 2 207.20 | 4.0 |
| 2 208.49 | 8.7 |
| 2 223.97 | 2.2 |
| 2 240.74 | 2.7 |
| 2 242.03 | 2.1 |
| 2 291.05 | 6.5 |
| 2 324.59 | 3.5 |
| 2 341.36 | 2.1 |
| 2 423.92 | 2.5 |
| 2 523.25 | 2.6 |
| 2 607.11 | 2.0 |
| 2 689.67 | 3.2 |
| 2 723.21 | 2.3 |
| 2 739.98 | 2.0 |
| 2 839.31 | 3.7 |
| 2 921.87 | 2.8 |
| 2 938.64 | 2.3 |
| 2 955.41 | 4.9 |
| 3 137.30 | 3.1 |
| 3 138.59 | 3.0 |
| 3 170.84 | 2.4 |
| 3 253.40 | 2.4 |
| 3 254.69 | 3.1 |
| 3 286.94 | 6.5 |
| 3 288.23 | 3.2 |
| 3 303.71 | 2.9 |
| 3 320.48 | 2.8 |
| 3 354.02 | 2.4 |
| 3 370.79 | 3.5 |
| 3 403.04 | 4.7 |
| 3 436.58 | 3.5 |
| 3 453.35 | 2.9 |
| 3 470.12 | 3.9 |
| 3 486.89 | 3.0 |
| 3 502.37 | 2.2 |
| 3 569.45 | 4.3 |
| 3 586.22 | 2.9 |
| 3 602.99 | 3.4 |
| 3 619.76 | 2.1 |
响应谱分析将模态分析的结构与一个已知的频谱联系起来计算模型的位移与应力,是一种确定性的瞬间载荷振动分析。而对于缸套的加速度信号是由气流与活塞、气缸作用后传递出,机组材料为结构钢,阻尼比小于0.01,采集仪测得的振动数据与真实的作用到活塞上振动信号的频域成分完全一致,且大小近似。
把表 3中各个频率对应的幅值作为激励源在XYZ方向同时载入到活塞组件表面作为响应谱分析[3-7],分析结果如图 6所示。

|
| 图 6 活塞组件的响应谱分析 Fig.6 Response spectrum analysis of the piston assembly |
图 6a、图 6b和图 6c分别表示X、Y和Z方向的变形位移图。图 6d是3个方向位移矢量图。活塞组件在3个方向(X、Y、Z方向)上的变形都较小,X和Y方向的变形位移分布相似,Z方向上的变形最大位置分布在活塞环处。从图 6e的等效应力分布云图可以看出,受到确定的振动载荷时,活塞环处的振动相比其他部位较大。对于国产活塞的安全因子计算如图 6f所示,该活塞结构腰部仍是相对薄弱的部位,其余部位的安全因子均大于1。因此,该往复压缩机的国产活塞组件在曲轴旋转角为0°时,受到本身确定性瞬态载荷振动时的破坏性低,符合当前的工作条件。
4 结论(1) 通过对该台往复压缩机活塞组件的模态分析,可知活塞的激振力频率均远小于其固有频率,因此国产活塞不会发生共振破坏。
(2) 在模态分析的基础上,对其进行响应谱分析,结果表明国产活塞组件工作时的变形、应力和安全因子均在许可范围内,验证了油田对往复压缩机活塞部件国产化改造工作的合理性,同时也为该类活塞安全性评定提供了依据。
(3) 研究结果对油田动设备零部件工作过程的评估方法提供了参考,也为国产活塞后期的推广应用奠定了基础。
| [1] | 尹汉军, 刘昌领, 姜瑛, 等. 基于ANSYS Workbench的采油树管道响应谱分析[J]. 石油矿场机械, 2015, 44(1): 13–16. |
| [2] | 唐振杰, 史展飞, 胡海涛. 不同频率激励下LY12铝合金悬臂梁的疲劳特性[J]. 材料科学与工程, 2012(6): 384–388. |
| [3] | 吴文秀, 曾云, 邹刚, 等. 某450T海洋井架的谐响应分析[J]. 石油机械, 2016, 44(6): 75–77. |
| [4] | 刘昌领, 陈建义, 李清平, 等. 基于ANSYS的六缸压缩机曲轴模态分析及谐响应分析[J]. 流体机械, 2012(8): 17–21. |
| [5] | JAISWAL O R, NARSUDE S, MATE N. Effect on structural design due to loss of sign in response spectrum analysis[J]. Indian Concrete Journal, 2012, 86(8): 33–38. |
| [6] | 胡超, 张来斌, 段礼祥, 等. 基于冗余第二代小波变换的振动信号降噪[J]. 石油机械, 2010, 38(10): 4–6. |
| [7] | JAYARAMAN S, MANISH T. Response spectrum analysis of printed circuit boards subjected to shock loads[J]. Procedia Engineering, 2016, 144: 1469–1476. DOI: 10.1016/j.proeng.2016.06.710 |




