2. 江苏省绿色过程装备重点实验室
2. Jiangsu Provincal Key Laboratory of Green Process Equipment
0 引言
旋流分离器以其结构简单、操作方便和占地面积小等优点而被广泛应用于化工、石油、有色冶金及食品等领域。其中,采用旋流分离方法进行油田污水处理可快速有效地去除直径较大的浮油和分散油,简化后续处理盐类和固体颗粒的工艺流程,使得深度处理后的污水达到排放或油田回注的要求[1]。相比于液-固分离,液-液分离更加复杂,因为油水两相密度差较小,旋流器内高速旋转的流体剪切力及湍动作用容易造成油滴的破碎和聚并, 在严重情况下, 两不相溶的液相还可能发生乳化现象。因此, 油滴破碎和聚并是影响油水分离水力旋流器分离效率的一个重要因素。
旋流器的液-液分离过程中存在强湍流和剪切力的作用,这将导致油滴发生破碎和聚并,直接影响分离效率。随着CFD技术的发展,采用数值模拟方法研究油滴破碎和聚并对分离效率的影响变得越来越成熟。S.STEFFEN等[2]使用CFD模拟方法对水和柴油在旋流器中的分离进行研究,发现油滴的破碎和聚并影响水和油的分离,并分析了影响柴油油滴粒径分布的因素。M.MEYER等[3]运用CFD技术模拟了不同的油滴体积分数和直径对油滴破碎和聚并的影响。S.NOROOZI等[4]运用CFD技术模拟了不同结构的旋流腔内油滴破碎和聚并的现象,得到了其对分离效率的影响。
笔者利用雷诺应力模型(RSM)和欧拉模型并加入群体平衡模型,数值模拟了液-液分离水力旋流器内油滴破碎和聚并现象,同时分析了不同入口油相体积分数、入口流量和不同结构对油滴破碎、聚并以及分离效率的影响。所得结论可为水力旋流器的现场应用提供指导。
1 数学模型 1.1 控制方程水和油两相的连续性方程如下[5]:
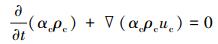
|
(1) |
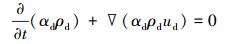
|
(2) |
式中:α、ρ和u分别表示体积分数、密度和速度,下标c和d分别表示连续相(水)和分散相(油)。
1.2 欧拉模型采用欧拉-欧拉的方法模拟液-液两相流。在此方法中,每一相都有单独的质量和动量守恒方程,对于不可压缩流体来说,每一相的平均动量方程表示如下:
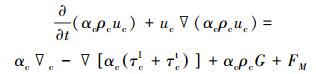
|
(3) |
式中:G为重力;FM是两相间的转换动量或两相之间的作用力,包括曳力、升力、虚拟质量力和湍流耗散力;τ为应力张量;上标l和t分别表示层流和湍流。
考虑油滴直径小以及2相间的密度相差小,忽略升力和虚拟质量力对油滴的影响。因此只考虑曳力和湍流耗散力。曳力的计算公式如下:
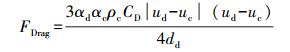
|
(4) |
根据Schiller-Naumann经验公式,曳力系数为:
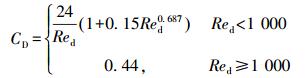
|
(5) |
式中:Red为油滴的雷诺数。
湍流耗散力表示为:
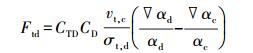
|
(6) |
式中:CTD是湍流耗散系数,vt, c是湍流运动黏度,σt,d是湍流施密特数[6]。
1.3 群体平衡模型群体平衡模型用于计算分散相油滴的粒径分布以及油滴破碎和聚并对油滴粒径分布的影响。群体平衡方程的一般形式为:
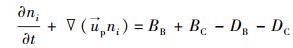
|
(7) |
式中:BB和BC均为产生率;DB和DC均为损失率;下标B和C分别表示破碎和聚并。
常见的群平衡数值解法有:离散法、矩方法、蒙特卡罗法和有限元法。笔者选择离散化的方法求解群体平衡方程,其基本思想就是将分散相分成几组不同粒径尺寸的油滴群。每一组油滴的数密度与油滴体积分率的关系为:
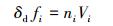
|
(8) |
式中:δd为分散相的体积分率;fi为第i组油滴的体积分率;Vi为对应第i组单个油滴的体积[7]。
1.4 湍流模型湍流的基本方程组包括连续性方程、雷诺方程、雷诺应力方程、湍动能方程以及湍动能耗散率方程等。
采用雷诺应力模型(RSM)对雷诺应力进行处理,RSM模型本身的优点就是自动考虑旋流效应、浮力效应、曲率效应和近壁效应并且充分考虑流体旋转或流线弯曲所带来的应力张量的急剧变化,适合模拟旋流器的复杂流场。由于在雷诺方程中出现了新的脉动速度的二阶关联项,即雷诺应力项,它与连续性方程不能封闭, 需要选择适当的湍流模型以使方程组封闭。模型化后的雷诺应力输运方程如下:
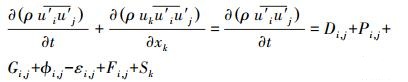
|
(9) |
式中:Sk为用户自定义的源项;Di, j为扩散项;Pi, j为应力产生项;Gi, j为浮力产生项;ϕi, j为应力应变再分配项;εi, j为离散相;Fi,j为旋转系统产生项。
模型化后的湍动能方程如下:
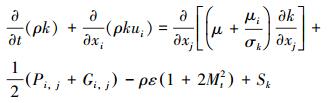
|
(10) |
式中:Mt为湍流马赫数。
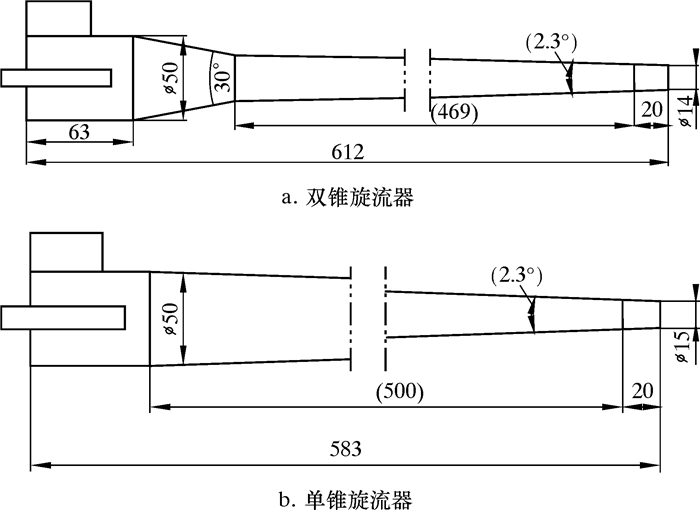
2 数值模拟 2.1 物理模型及网格划分笔者主要选用2种不同结构的旋流器来探索其对油滴破碎和聚并的影响:一种是单切向入口双锥旋流器,如图 1a所示;另一种是单切向入口单锥旋流器,如图 1b所示。
|
| 图 1 不同结构的旋流器结构示意图 Fig.1 Structural schematic diagram of cyclone with different structures |
根据油滴在水中破碎的结构特点对模型进行网格划分,计算区域采用结构化网格。双锥旋流器网格数为175 000,如图 2a所示;单锥旋流器网格数为172 800,如图 2b所示。

|
| 图 2 旋流器网格划分图 Fig.2 Cyclone meshing |
2.2 入口油滴粒径分布
模拟过程中设定连续相为水,分散相为油,其物理属性如表 1所示。
| 物质 | 密度/(kg·m-3) | 黏度/(Pa·s) | 表面张力/(N·m-1) |
| 油 | 730 | 24 | 0.026 |
| 水 | 998 | 1 | — |
入口处的油滴粒径分为12组油滴群,每组油滴的尺寸分布如表 2所示。此外,由于破碎和聚并产生的油滴粒径分布变化可以通过比较入口油滴粒径分布和真实的油滴粒径分布来反映。真实的油滴粒径分布可以通过计算底流和溢流的油滴粒径分布来实现[2-3]。
| 组数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 油滴粒径/mm | 5.34 | 4.76 | 4.24 | 3.78 | 3.36 | 3.00 | 2.67 | 2.38 | 2.12 | 1.89 | 1.68 | 1.50 |
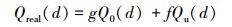
|
(11) |
式中:g和f是溢流和底流处油滴的体积积分。
2.3 边界条件和计算条件设定入口采用速度入口,并设置速度为4 m/s,底流和溢流均为压力出口。选用Pressure Based隐式求解器;单相1阶模拟控制方程中压力-速度耦合项选用SIMPL数值算法;单相3阶选择SIMPLEC算法;油水两相模拟3阶,采用QUICK算法;应用PERSTO压力差补格式,其他参数保持系统默认值[8-10]。
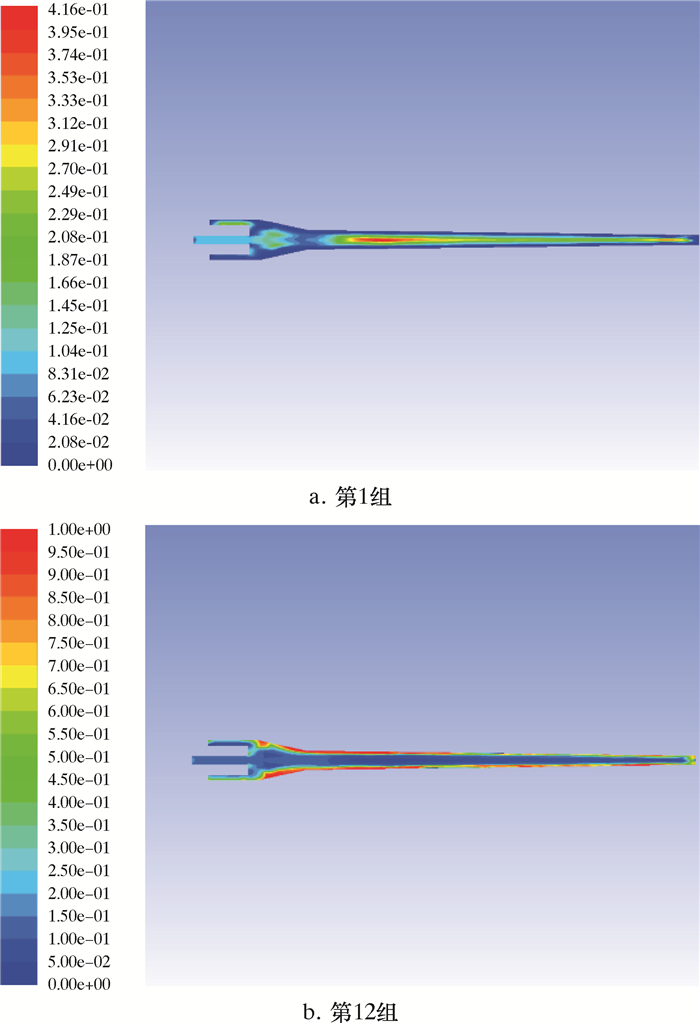
3 模拟结果分析 3.1 油滴组体积分布选择最大粒径(第1组)和最小粒径(第12组)的油滴进行比较,图 3为2组油滴在旋流器纵向截面处的体积分数分布云图。从图 3a可以看出,第1组油滴群的体积分数在中心区域比其他区域要大,这是因为油滴受到离心力的作用,使得其从壁面处移动到中心区域,同时也提高了油滴间发生碰撞的可能性,所以在旋流器的中心区域油滴更容易聚并。从图 3b可以发现,第12组油滴群主要分布在旋流器的壁面附近,这是因为在此处流体动能耗散率非常大,使得油滴的破碎率更高,油滴发生破碎的可能性更大。
|
| 图 3 不同组油滴体积分数分布云图 Fig.3 Distribution of the volume fraction of oil droplets in different groups |
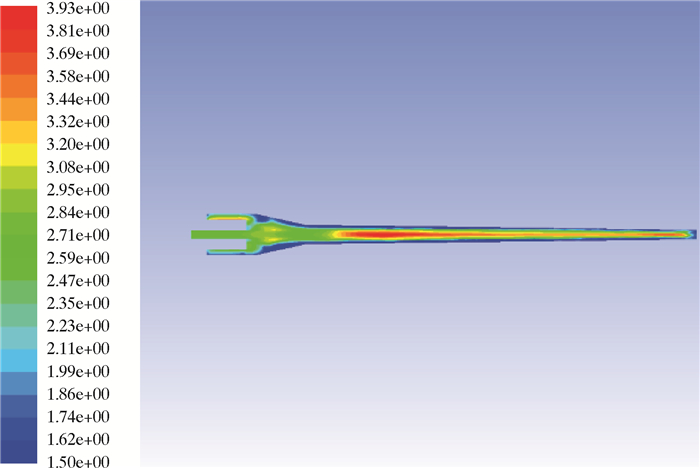
图 4为油滴的索特尔平均直径分布图。从图可以看出,油滴的聚并主要发生在中心区域,破碎则主要发生在壁面附近。
|
| 图 4 油滴索特尔平均直径云图 Fig.4 Sauter average diameter cloud of oil droplets |
3.2 不同入口流量的影响
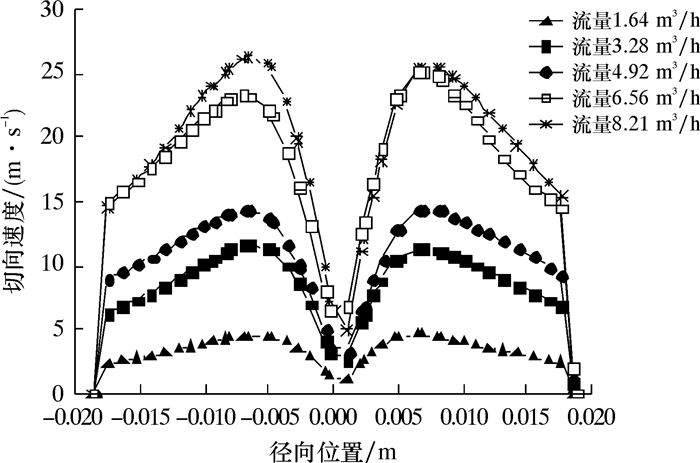
图 5和图 6分别为5种不同入口流量下切向速度和湍流耗散率的变化曲线。从图 5可以看出,自轴心至壁面,切向速度先增大后减小,并且随着入口速度的增大,其切向速度也在增大。
|
| 图 5 不同入口流量下切向速度沿径向分布曲线 Fig.5 The tangential velocity distribution along the radial direction at different inlet flow rates |
|
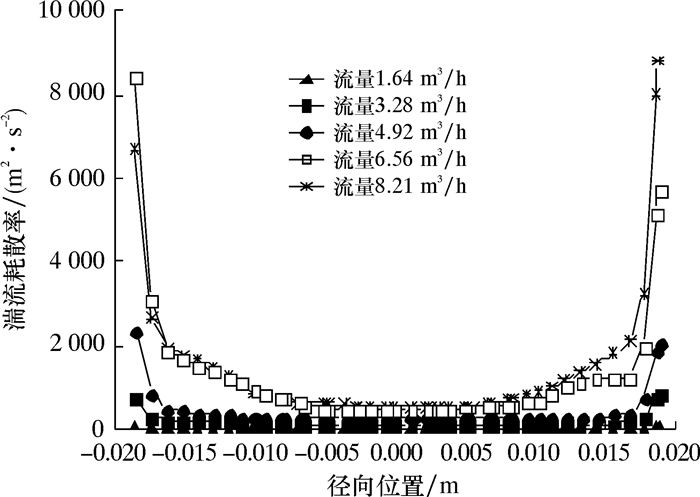
| 图 6 不同入口流量对湍流耗散率的影响曲线 Fig.6 Influence of inlet flow rate on turbulent dissipation rate |
从图 6可以看出,靠近壁面处的湍流耗散率最大,并且随着入口速度的增大,湍流耗散率在增大。由此可见,增大入口速度,一方面能够增大切向速度,进而可以提高分离效率,另一方面也增加了湍流耗散率,这将会促进油滴的破碎。特别是在靠近壁面区域,湍流耗散率的提高使得油滴破碎现象更加严重。
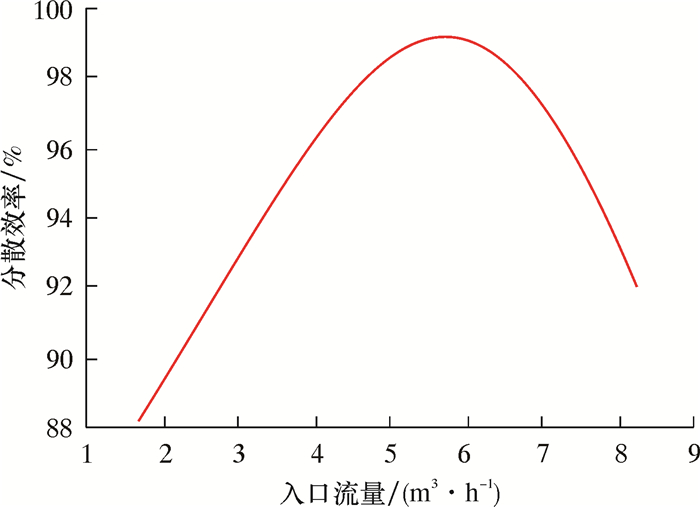
综上所述,虽然随着入口流量的增大,切向速度在增大,对分离效率有所提高,但是增大入口流量的同时,油滴破碎的现象逐渐占据主导作用,对分离效率的提高并不会有所改善,这一点从图 7也可以证实。
|
| 图 7 不同入口流量对分离效率的影响曲线 Fig.7 Influence of inlet flow rate on the separation efficiency |
由图 7可以看出,起初增加入口流量分离效率会提高,但是随着流量的增大分离效率会降低,因此存在一个最佳处理量。针对笔者所讨论的固定结构尺寸的旋流器,其最佳处理流量范围为4.92~6.56 m3/h,对应的分离效率为99.36%~99.58%。
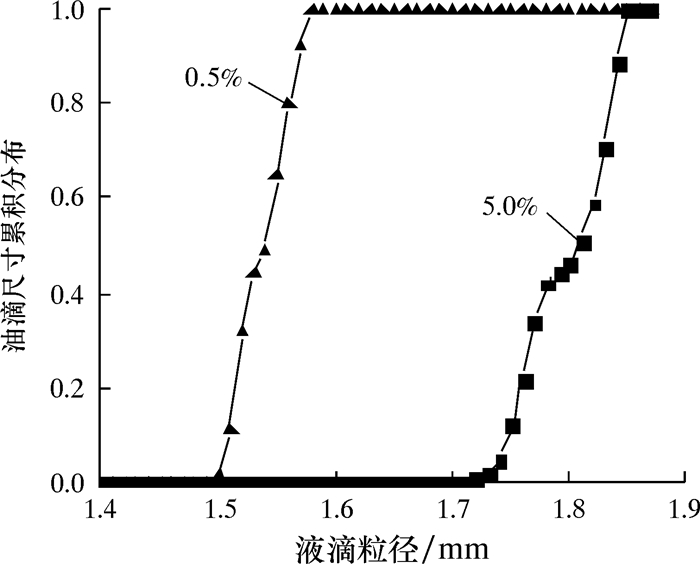
3.3 分散相体积分数的影响图 8是入口油相体积分数分别为0.5%和5.0%时油滴尺寸累积分布,即小于等于任意粒径油滴占所有油滴的比例。从图可以看出,随着油相体积分数的增加,油滴发生聚并现象更加明显。这是因为体积分数增加使油滴发生碰撞的概率提高,进而油滴更容易发生聚并。
|
| 图 8 不同体积分数时油滴累积尺寸分布图 Fig.8 Cumulative size distribution of oil droplets with different concentrations |
3.4 单锥和双锥的分离效率对比
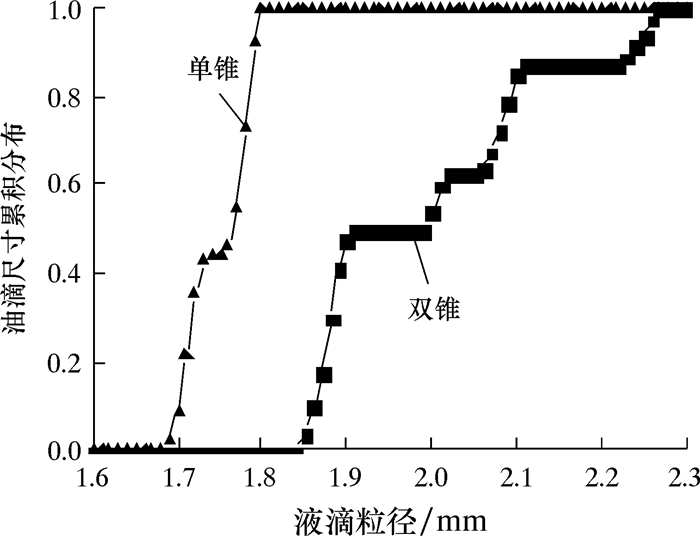
图 9为2种结构旋流器油滴尺寸累积分布图。
|
| 图 9 不同结构旋流器油滴尺寸累积分布图 Fig.9 Cumulative size distribution of oil droplets under different cyclone structures |
从图 9可以看出,双锥旋流器的油滴粒径分布向粒径大的方向移动。这说明与单锥旋流器相比,双锥旋流器中液滴更容易发生聚并。
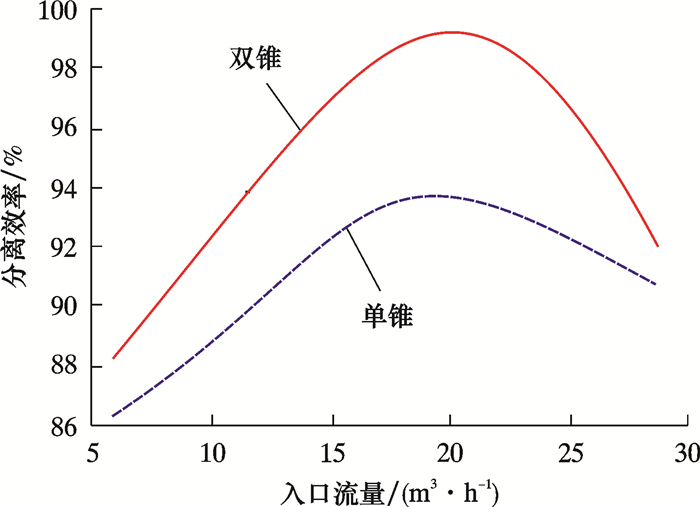
图 10为不同结构旋流器分离效率曲线。从图可以看出,双锥旋流器的分离效率高于单锥旋流器分离效率。双锥结构对流体的动量补偿优于单锥结构,其湍流强度较弱,油滴聚并现象更明显,适合密度差较小的液-液分离。
|
| 图 10 不同结构旋流器分离效率曲线 Fig.10 The separation efficiency curve of cyclones with different structures |
4 结论
(1) 在旋流器中,油滴的破碎主要发生在近壁面处,此区域湍流耗散比较大使得油滴破碎;油滴的聚并主要发生在中心区域,油滴受到向心力的作用,使得其由壁面向中心迁移,在此过程中油滴发生碰撞的概率提高,更容易发生聚并。
(2) 随着入口流量的增大,油滴的聚并现象逐渐明显,但其湍流耗散率也随之增大,分离效率先升高后降低,因此某一固定结构的旋流器均存在一个最佳处理量范围,双锥结构的旋流器最佳处理量范围是4.92~6.56 m3/h。
(3) 增加油相的体积分数会抑制油滴的破碎,提高油滴碰撞概率,从而促进油滴的聚并。
(4) 与单锥旋流器相比,双锥旋流器为油滴碰撞提供了更多的机会,油滴更容易聚并;通过比较两者的分离效率,双锥旋流器的分离性能更好。
| [1] | 袁惠新, 殷伟伟, 黄津, 等. 固液分离旋流器壁面磨损的数值模拟[J]. 化工进展, 2015, 34(3): 664–670. |
| [2] | STEFFEN S, GORBACH G, PIESCHE M. Modeling fluid behavior and droplet interactions during liquid-liquid separation in hydro cyclones[J]. Chemical Engineering Science, 2009, 64(18): 3935–3952. DOI: 10.1016/j.ces.2009.04.046 |
| [3] | MEYER M, BOHNET M. Influence of entrance droplet size distribution and feed concentration on separation of immiscible liquids using hydrocyclones[J]. Chemical Engineering and Technology, 2010, 26(6): 660–665. |
| [4] | NOROOZI S, HASHEMABADI S H. CFD Simulation of inlet design effect on deoiling hydrocyclone separation efficiency[J]. Chemical Engineering and Technology, 2010, 32(12): 1885–1893. |
| [5] | 尹巧朵. 水力旋流器油水分离及液滴破碎数值模拟研究[D]. 武汉: 华中科技大学, 2014. |
| [6] | NOROOZI S, HASHEMABADI S H, CHAMKHA A J. Numerical analysis of drops coalescence and breakage effectson de-oiling hydrocyclone performance[J]. Separation Science and Technology, 2012, 48(7): 991–1002. |
| [7] | 左晶, 王娟, 王江云, 等. 采用群体平衡模型模拟多段环流反应器内的气-液两相流动[J]. 石油学报(石油加工), 2016, 32(6): 1134–1141. |
| [8] | LUO H, SVENDSEN H F. Theoretical model for drop and bubble break up in turbulent dispersions[J]. Chemicol Engineering Science, 1996, 42(5): 766–776. |
| [9] | KO J, ZAHRAI S, MACCHION O, et al. Numerical modeling of highly swirling flows in a through-flow cylindrical hydrocyclone[J]. AIChE J., 2006, 52(10): 3334–3344. DOI: 10.1002/(ISSN)1547-5905 |
| [10] | SLACK M D, PORTE D S, ENGELMAN M S. Designing automated computational fluid dynamics modeling tools for hydrocyclone design[J]. Minerals Engineering, 2003, 17(3): 705–711. |



