0 引言
气藏开采至中、后期,能量消耗增多,气藏处于低压低产开采阶段[1]。气井中由于气体不能有效携带出液体而使液体在井筒中积聚形成“气井积液”[2-4]。当液体积聚到一定程度时,开始侵入近井区域的储层,逐渐积累导致产量下降,生产时间缩短,甚至停产。针对苏里格气田的开发特征,笔者提出将射流泵与涡流工具相结合的排水采气工艺,设计射流涡流排水采气装置,在不借助外界动力源的情况下,充分利用地层能量将积液排出井筒,以提高气井采收率和开发经济性。
涡流排水采气工艺是近年来引进石油行业的一项创新技术,它既可以应用于气井井下作业,也可以应用于地面输气[5]。国内外对于涡流排水采气工艺的研究主要从结构设计、流体分析和试验3方面展开。杨涛等[6-7]开展了涡流工具的结构设计。M. SURENDRA等[8]利用CFD方法建立了涡流排水采气稳态模型,利用数值模拟计算,研究了气液混合物流经涡流工具后的密度分布和速度分布等流动规律。稳态模型在一定程度上体现了涡流工具中的流体分布情况,但稳态控制方程中没有时间项,这会对结果的可靠性产生影响。笔者在此建立稳态模型进行分析,将其结果作为瞬态模型的初始值,以期更为准确地模拟真实的流体状况。美国和加拿大的多家石油公司开展了井下涡流工具排水采气试验及应用。国内在长庆、大庆和青海等气田开展了多项涡流工具排水采气试验[9-11]。从使用效果的评价分析来看,涡流工具排水采气工艺可以有效降低气液流动阻力,提升采气速度,增强气流的携液能力。
目前射流技术非常成熟,在气井排水采气方面的应用也较多。射流泵通过高速射流提升低速被吸液体的能量,从而增加整体压能,这一特点若能与涡流工具结合起来,将能够更好地发挥射流泵的作用,但目前鲜少报道将射流泵与涡流技术相结合的排水采气工艺及新型设备。鉴于此,中国石油长庆油田分公司第五采气厂开展了涡流工具与射流技术相结合的排水采气工艺机理研究、影响因素及设备研发等系列工作。
1 模型建立及结构设计 1.1 计算模型射流涡流装置的气液流动过程为气液混合,因此计算流域的数值模拟计算采用气液混合模型(Mixture)。混合模型可模拟各相不同速度的多相流,并假定短空间尺度局部平衡,允许相之间互相贯穿,因此控制体积的体积分数为0~1之间的任意值[12]。此模型考虑了离散相和连续相的速度差,及其相互之间的作用,动量方程及连续性方程各物性参数采用各相体积平均值。混合模型的控制方程如下。
连续性方程:
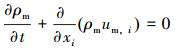
|
(1) |
动量方程:
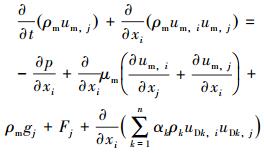
|
(2) |
第2相的体积分数方程:
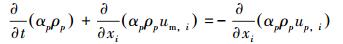
|
(3) |
式中:n为相数;αk为第k相的体积分数;αp为第2相的体积分数;ρm为混合密度,kg/m3;ρk为第k相密度,kg/m3;ρp为第2相密度,kg/m3; p为压力,MPa;um为质量平均速度,m/s;uDk为第k相的漂移速度,uDk=uk-um,m/s;μm为混合黏度,Pa·s;Fj为体积力,N;gj为重力加速度,m/s2。
1.2 结构设计基于苏东61-39井的现状设计了射流涡流排水采气装置。苏东61-39井于2009年11月开始投产,初始油压13.5 MPa,套压23.0 MPa,日产气量17.7×104m3,投产后半年内油压保持在6~7 MPa,套压逐渐减小,平均日产气量超过105 m3。随着开采时间的延长,日产气量逐渐降低,产水量开始上升,从2014年至今,平均日产气量降为2.0×104 m3,井口油压降为5.54 MPa,套管压力降为5.89 MPa,其中多次关井,最短3 d,最长40 d,在恢复生产后日产气量有所提升,但持续时间短,且产量不稳定。
图 1为射流涡流排水采气装置结构示意图。该装置通过打捞头沿油管下放到预定位置后,由接箍挡环卡在2根相邻油管与油管接箍的缝隙处,将工具固定。井底气体从油管进入喷射接头,并由喷嘴进入喉管,在这一过程中,由于喷射接头为变径体,使气体势能减小,动能增大,从喷嘴进入喉管时流速增加,在喷嘴附近产生低压区,喉管附近的液体通过压差沿喉管上的豁口进入喉管,并与气体混合。混合流体在喉管中混合均匀后通过连接在上方的导流管扩散进入油管,并沿着绕流器流动,此时混合流体流动状态变为旋流,气水两相分离,密度较大的水被甩向井壁,气体在管道中心流动,从而减小了气液两相流体在行进中相互摩擦造成的能量损失。因此该结构可降低管线对流体的流动摩阻与滑脱损失,同时还可提高两相流体的流速,从而排出井底积液。

|
| 图 1 射流涡流排水采气装置 Fig.1 Jet vortex drainage gas recovery device 1—喷射接头;2—喉管;3—导流管;4—绕流器。 |
1.3 数值模型及模拟条件设定
根据射流涡流排水采气装置的结构模型,建立其数值模型,如图 2所示。为了分析气液两相流在射流涡流排气采气装置中的流动情况,用布尔运算抽取流体模型。考虑到射流和涡流运动中有与旋转及曲率相关的因素,湍动黏度计算公式会发生变化,因此选择可适应于包含射流等自由流动的多种流动方式的RSM模型。RSM模型比单方程和双方程模型更加严格地考虑了流线型弯曲、漩涡、旋转和张力快速变化,它对于复杂流动有更高精度的预测潜力。

|
| 图 2 射流涡流排水采气装置数值模型 Fig.2 Numerical model of jet vortex drainage and gas recovery device |
为了计算的准确性,先进行稳态计算,其初始条件设置如下:入口1为速度入口,入口2为压力入口。设气相为第1相,液相为第2相,气液比为0.9。设置入口处气液混合相的边界条件,其中入口1水力直径为104 mm,入口2水力当量直径为94 mm,湍流强度近似为5%。出口边界设置为outflow,流动完全发展,出流面上的流动情况由区域内部外推得到,且对上游流动没有影响。稳态计算结束后,将稳态计算结果作为瞬态计算的边界条件,初始化条件选择all zone,选用标准壁面函数处理壁面边界层流场。
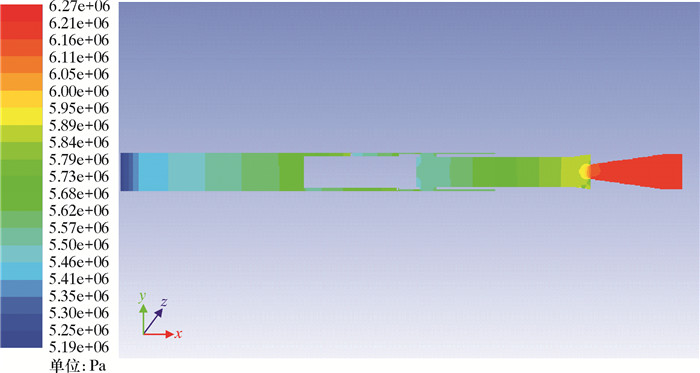
2 模拟结果及分析 2.1 截面压力分布图 3为射流涡流排水采气装置在气液比为0.9工况下xy截面的总压分布图。由图可以看出,从喷射接头气体入口端至气液出口端,压力逐渐降低。为了表示其结构各位置变化幅度,用曲线图来进一步说明。
|
| 图 3 xy截面总压分布 Fig.3 Total pressure distribution at xy cross section |
图 4为整个流体区域压力曲线图。图中以入口1端面作为横坐标零点位置,横坐标为流体区域轴向方向坐标,纵坐标为总压力。

|
| 图 4 流体区域压力曲线图 Fig.4 Pressure curve of fluid domain |
图 5为整个流体区域与轴向上的压力曲线对比(白色为整个流体区域,红色为轴向)。由图 4和图 5对比可见,除涡流螺旋段外,在同一截面的压力变化很小,即可以用轴向上的压力分布来表示整个流体区域的压力分布。

|
| 图 5 流体区域与轴向压力曲线对比 Fig.5 Comparison of pressure curve between fluid domain and along axial direction |
由图 5可以看出,在整个流体区域内,按照其压力发展变化特点,可分为6个区域:1为喷射接头内流体区域;2为积液区入口流体区域,受入口截面图形边界的影响,压力波动较大;3为喉管内流体区域;4为涡流螺旋内流体区域;5为油管内流体区域;6为油管末端流体区域。区域5和区域6同为油管内流体区域,由于边界条件中设定了油管出口端压力为5.2 MPa,所以该区域压力斜率与区域5不同。1、2、3为流体输入区域,4、5、6为流体运动结果区域,其中区域6受边界条件设置控制,因此以下重点分析区域4和区域5。
图 6为区域4(涡流螺旋部分)在不同截面上径向的压力分布曲线图。图中4条不同颜色的线条分别代表了距离入口端0.80、0.85、0.90和0.95 m的截面压力分布。由图可以看出,4条线近似都为螺旋线,且螺距相同,螺旋线的起始与终止处的纵坐标差值反映了螺旋结构两侧的压力差,4条线的压力差都约为0.3 MPa,可见在同一截面上的压差比射流涡流排水采气装置其他结构大。因此该压力差值也表明了该螺旋结构有进一步将气液分离的作用。

|
| 图 6 区域4在径向上的压力分布 Fig.6 Pressure distribution of Area 4 in the radial direction |
图 7a为区域5在不同截面上径向的压力分布云图。从距离入口不同位置的截面上可见压力的变化,为得到在不同截面径向分布的压力变化,进一步用曲线图的方式来反映压力数值变化。图 7b为区域5(油管部分)不同截面上的压力分布曲线图。图中6条不同颜色的线条分别代表了距离入口端1.10、1.15、1.20、1.25、1.30和1.35 m在径向上的压力分布。由图可见,6组线均可近似看作直线,且互相平行,在同一截面上的压力数值相同,互相平行且间距几乎相等,即距离入口端越远,压力越小,并且压力下降的幅度基本相同。这与喉管段的压力分布特点类似。

|
| 图 7 区域5压力分布 Fig.7 Pressure distribution of Area 5 |
2.2 井下工况对流场的影响分析 2.2.1 流速对压降的影响
图 8为射流涡流排水采气装置入口速度对压降的影响。设定涡流结构螺旋角为70°,含液体积分数为20%,改变入口流速对进出口持液率差值和进出口压降进行分析。

|
| 图 8 流速对压降的影响 Fig.8 Effect of flow rate on pressure drop |
以射流结构的出口端为涡流结构入口端,取x轴数值为-0.77 m为涡流结构入口端,以整体结构的出口端为出口,改变进口速度,观察进口速度对管道压降的影响。由图 8可知,随着入口速度的增加,压降呈升高趋势,即流速越大,压力损失越大,且随着流速的增加压力损失增加趋势加大。
2.2.2 含液体积分数对压降的影响图 9为射流涡流排水采气装置含液体积分数对压降的影响。设定涡流结构螺旋角为70°,入口速度为7.6 m/s,针对不同螺旋角度的射流涡流排水采气装置进出口持液体积分数差值和进出口压降进行分析。以射流结构的出口端为涡流结构入口端,取x轴数值-0.77 m为涡流结构入口端,以整体结构的出口端为出口,改变入口含液体积分数,观察含液体积分数对管道压降的影响。通过数值计算,并进行压降规律分析。由图 9可知,随着含液体积分数的增加,压降呈升高趋势。

|
| 图 9 含液体积分数对压降的影响 Fig.9 Effect of liquid fraction on pressure drop |
2.3 结构参数对流场的影响分析
通过有限元分析模拟射流涡流排水采气装置的流场分布,其中涡流部分螺旋结构参数对携液有着直接影响。因此以螺旋结构参数作为优化对象,改变各参数的数值,根据其对持液体积分数的变化来选择最优参数。
2.3.1 螺旋角的影响图 10为射流涡流排水采气装置螺旋角对排液效果的影响。设定整体结构的进口流速为7.6 m/s,针对不同螺旋角的射流涡流排水采气装置对进出口持液体积分数差值和进出口压降进行分析。以射流结构的出口端为涡流结构入口端,取x轴数值-0.77 m为涡流结构入口端,以整体结构的出口端为出口。

|
| 图 10 螺旋角对排液效果的影响 Fig.10 Effect of helix angle of drainage gas recovery device on discharge efficiency |
由图 10a可见,当螺旋角为40°~55°时,进出口持液体积分数差值随着螺旋角的增加而增加;当螺旋角为55°~70°时,进出口持液体积分数差值随着螺旋角增加而减小;螺旋角大于70°以后,持液体积分数差值又随着螺旋角增加而增加。可见螺旋角在70°左右时,持液体积分数差值最小,排液效果最佳,携液能力最好。
由图 10b可见,当螺旋角为40°~50°、65°~75°时,压降较小;当螺旋角为50°~65°时,压降较大。可见螺旋角在45°或70°左右时,进出口压降较小。
2.3.2 螺旋槽深的影响图 11为射流涡流排水采气装置螺旋槽深对持液体积分数差值的影响。由图可见,排液效果最佳时的螺旋槽深为4 mm,在5 mm时次之。当螺旋槽深度值较小时(小于4 mm),螺旋槽底部与螺旋槽较浅位置处的速度梯度变化不大,使得螺旋槽深的变化对排液效果的影响并不大,当螺旋槽深大于等于4 mm时,随着螺旋槽深的增加,排液效果明显降低。经分析,这一现象产生的原因是离心力作用,螺旋槽底部处的流体剪切力为螺旋槽内最大值,因此靠近螺旋槽底部处的流体阻力系数大于螺旋槽较浅位置处的流体阻力系数,即槽深增加,加大了最外壁面的半径,流动损失增加,因此排液效果也随之降低。

|
| 图 11 螺旋槽深对持液体积分数差值的影响 Fig.11 Effect of spiral groove depth on the difference of liquid volume fraction |
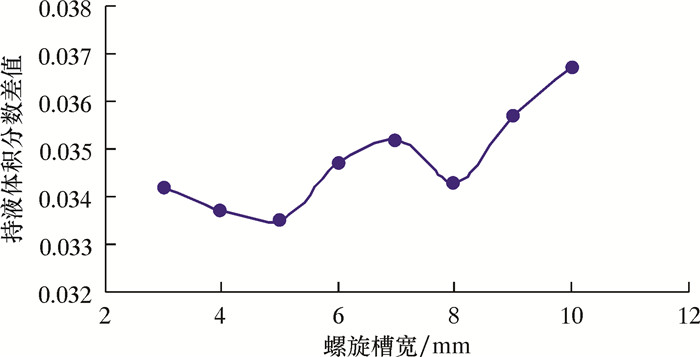
2.3.3 螺旋槽宽的影响
图 12为射流涡流排水采气装置螺旋槽宽对持液体积分数差值的影响。由图可见,排液效果最佳时,螺旋槽宽的取值范围为4~6 mm,其中5 mm时排液效果最佳。随着螺旋槽宽的增加,排液效果整体呈降低趋势。经分析,这是由于螺旋槽宽减小,则流体的过流面积减小,流体速度会得到提升,携液能力便可增强。但随着螺旋槽宽的进一步减小(小于5 mm),气液得不到有效分离,流体所受阻力增加,造成压力损失增大,携液能力减弱,因此排液效果也随之降低。
|
| 图 12 螺旋槽宽对持液体积分数差值的影响 Fig.12 Effect of spiral groove width on the difference of liquid volume fraction |
3 结论
(1) 涡流螺旋处不同截面径向的压力分布曲线为近似螺旋线,且螺距相同,螺旋线的起始与终止处的纵坐标差值反映了螺旋结构两侧的压力差,该压力差值比其他位置压力差值大,表明该螺旋结构有进一步将气液分离的作用。油管处不同截面上的压力分布曲线图可近似看作直线,在同一截面上的压力数值相同,互相平行且间距几乎相等,即距离入口端越远,压力越小,并且压力下降的幅度基本相同。
(2) 随着入口速度的增加,压降呈升高趋势,即流速越大,压力损失越大,且随着流速的增加,压力损失增加趋势加大;随着含液体积分数的增加,压降呈升高趋势。
(3) 当螺旋角为40°~55°时,进出口持液体积分数差值随着螺旋角的增加而增加;当螺旋角为55°~70°时,进出口持液体积分数差值随着螺旋角的增加而减小;当螺旋角大于70°,又随着螺旋角的增加而增加,即螺旋角为70°左右时,持液体积分数差值最小,排液效果最佳,携液能力最好。当螺旋角为40°~50°、65°~75°时,压降较小;当螺旋角为50°~65°时,压降较大。
(4) 排液效果最佳时的螺旋槽深为4 mm,在5 mm时次之。当螺旋槽深大于等于4 mm时,随着螺旋槽深的增加,排液效果明显降低。排液效果最佳时,螺旋槽宽的取值范围为4~6 mm,其中5 mm时排液效果最佳。随着螺旋槽宽的增加,排液效果整体呈降低趋势。
| [1] | 廖锐全, 曾庆恒, 杨玲. 采气工程[M]. 北京: 石油工业出版社, 2012: 128-147. |
| [2] | 田伟, 李谦定, 陈德见, 等. 苏里格气田连续油管排水采气试验及分析[J]. 石油化工应用, 2010, 29(6): 35–36. |
| [3] | 张荣军, 乔康. 柱塞气举排水采气工艺技术在苏里格气田的应用[J]. 钻采工艺, 2009, 32(6): 118–119. |
| [4] | 黄艳, 佘朝毅, 钟晓瑜, 等. 国外排水采气工艺技术现状及发展趋势[J]. 钻采工艺, 2005, 28(4): 57–60. |
| [5] | ALI A J, SCOTT S L, FEHN B. Investigation of a new tool to unload liquids from stripper gas wells[J]. SPE Production & Facilities, 2005, 20(4): 306–316. |
| [6] | 杨涛, 余淑明, 杨桦. 气井涡流排水采气新技术及其应用[J]. 天然气工业, 2012, 32(8): 63–67. |
| [7] | 杨旭东, 李丽, 张军, 等. 井下涡流工具排水采气机理研究[J]. 石油机械, 2015, 43(5): 81–86. |
| [8] | SURENDRA M, FALCONE G, TEODORIU C. Investigation of swirl flows applied to the oil and gas industry[J]. SPE Projects, Facilities & Contraction, 2009, 4(1): 1–6. |
| [9] | 朱庆, 张俊杰, 谢飞, 等. 涡流排水采气技术在四川气田的应用[J]. 天然气技术与经济, 2013, 7(1): 37–39. |
| [10] | 杨启明. 国外井下气液分离采气新技术研究现状分析[J]. 天然气工业, 2001, 21(2): 85–88. |
| [11] | 张春, 金大权, 王晋, 等. 苏里格气田井下涡流排水采气工艺研究[J]. 天然气技术与经济, 2012, 5(6): 45–48. |
| [12] | 邵乐. 低压低产气井涡流工具优化设计研究[D]. 西安: 西安石油大学, 2015: 23-25. http://cdmd.cnki.com.cn/Article/CDMD-10705-1015307422.htm |



