0 引言
海上漂浮输油软管是目前海上油田进行外输作业的重要设备[1],主要应用于FPSO、浮筒和穿梭油轮之间的原油输送。漂浮输油软管在海上进行临时中转和补给油料时,因能较快地进行铺设和撤收而被广泛使用。对海上漂浮输油软管进行受力分析对海上软管的安全运行具有重要作用[2]。
海上漂浮输油软管是一种易耗品,软管在无维修的情况下平均使用寿命为3 a,因此每2~3 a便需要更换1次。随着海上油田开采技术的快速发展,原油外输频率在逐年增加,海上漂浮软管的需求量也大大增加,国土资源部经严格和详实的测算,在我国在渤海和南海海洋石油开发中年需求量为3 600根以上。
根据海上漂浮输油软管工作条件,在重力、浮力以及波浪载荷和海流作用下,软管往往产生较大的扭转、弯曲和拉伸,容易造成错位、折裂、接头松脱甚至拉断。同时,船舶和浮筒运动所产生的应力也会与管组系统的固有应力耦合,使得海上漂浮软管系统的分析和设计都极为困难。因此,在软管初步设计阶段,建立漂浮管组的整体静态数学模型,得到其固有应力和平衡状态,可为其进一步的动态分析奠定基础[3]。
1 研究背景及现状海上漂浮输油软管为复杂的组合截面柔性结构,制造工艺复杂,造价高昂[4]。
漂浮软管由橡胶、帘布、加强钢筋和其他非金属材料等组成,结构如图 1所示。漂浮软管的抗弯刚度相对于钢管而言非常小。

|
| 图 1 漂浮软管结构 Fig.1 Floating hose structure |
悬链系泊(CALM)系统是一种单点系泊系统,它包括浮筒、系泊链、系泊缆绳、漂浮软管、水下软管、水下管汇和海底管道等设施[5]。海上漂浮管组系统一般通过钢制法兰连接组成。在CALM中通常除了和浮筒相连的第1根软管,管组中其余软管均有漂浮层。首管靠近浮筒的一端没有漂浮层,剩余部分均有漂浮层。首管无漂浮层的一端经过加强结构设计,增大了其拉伸和弯曲刚度,可以承受由于浮筒的运动产生的应力和应变,避免应力集中。同时,首管可以将浮筒运动产生的荷载分散到整个漂浮管组上[6]。漂浮软管工作状态如图 2所示。

|
| 图 2 漂浮软管工作状态图 Fig.2 Working state of floating hose |
由于浮筒的运动产生应力,使得与浮筒连接的第1和第2根软管预期寿命短于漂浮管组中其余软管的寿命。海上漂浮管组任意部分的失效都会出现大量溢油,造成严重的环境污染以及经济损失。因此,海上漂浮输油软管系统的设计和力学性能分析极为重要。
目前,对海上漂浮输油软管整体静态性能分析最初是基于经典的悬链线方程进行求解。国外A.P.K.DE ZOYSA[7]和A.H.PEYROT等[8]在分析海上漂浮软管整体静态力学性能问题时都采用了经典悬链线方程进行求解。该方法只对软管的自重和所受的海流力进行分析,没有考虑软管自身弯曲刚度产生的影响,因此,该方法分析得出的软管形态结果存在一定的误差,也难以计算出作用在软管上的弯矩[9]。孟浩龙等[1-2]在漂浮输油软管建模过程中,只考虑了管组的整体模型,忽略了浮筒对管组性能的影响。王猛等[5]利用Orcaflex软件模拟了水下输油软管组的静态和动态力学性能,但缺乏理论推导依据。
2 力学模型 2.1 物理系统通常在CALM系统中连接浮筒与油轮的漂浮软管依次为一端增强的首管、主管、变径管、尾管和围栏管,如图 3所示。穿梭油轮通过系泊缆停靠在浮筒附近。在静态作用下,首管与浮筒管汇接口通过法兰连接。

|
| 图 3 漂浮管组与浮筒模型 Fig.3 Model for floating hose group and float tank |
2.2 模型假设
为了建模计算方便,且考虑到变径管及尾管的结构与主管类似,质量相差较小,建模时将变径管与尾管当作主管来处理,即认为每种软管单位长度的质量都相等。
假设浮筒管汇接口距水平面距离为y,浮筒与首管接口处的管汇倾斜角为θ。
利用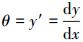
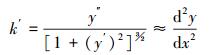
|
(1) |
由于漂浮管组的最大倾斜角θ通常很小,所以θ=tanθ=y′数值很小,(y′)2数值更小,可忽略不计。
2.3 力学模型漂浮管组在静态载荷作用下,首管受到自身重力、海水浮力以及浮筒管汇接口作用力,主管受自身重力和海水浮力。
由于首管与主管结构的不同,导致首管与主管的半径也不相同,漂浮管组中首管和主管半径的变化如图 4所示。

|
| 图 4 漂浮软管首管和主管结构图 Fig.4 Structure of the first hose and the main hose of the floating hose |
当管组从浮筒管汇接口出来,首管前段(无漂浮层)半径为r=ru。
首管与主管通过法兰相连接,首管具有漂浮层部分以及主管半径为r=rf。因此有:
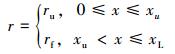
|
(2) |
式中:x为管组轴线总长度,xu为首管加强端(无漂浮层)的长度,xf为首管有漂浮层的长度,xL为管组总长度。
考虑到漂浮管组一端与浮筒相连接,另一端自由地漂浮在海面上,笔者主要计算海上漂浮软管组在静力载荷作用下的几何形态及内力分布。
3 载荷计算在管组静态分析中,只考虑管组承受自身重力、海水浮力以及浮筒管汇作用力。当管组漂浮在海面上时,管组单位长度受到的海水浮力为B,等于管组排开海水的重力。取管组与浮筒管汇接口为坐标原点,海平面为x轴,海平面竖直方向为y轴,建立整体管组坐标系。
3.1 管组完全浸没载荷通常在安装和实际工况下,首管全部浸没在海水中,则管组单位长度受到的浮力大小与管组浸没海水深度无关,只与管组半径有关,此时管组单位长度受到的浮力为:

|
(3) |
式中:ρ为海水密度,g为重力加速度。
3.2 管组漂浮载荷当管组漂浮在海平面时,计算管组单位长度受到的海水浮力。取z轴为水平面,O点为管组轴线位置,y为管组轴线距海平面竖直方向的距离(-r≤y≤r),如图 5所示。

|
| 图 5 软管漂浮水面示意图 Fig.5 Schematic diagram of the hose floating at water surface |
图 5中三角形AOB的面积为:

|
(4) |
管组沉入水中单位长度的体积为:
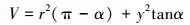
|
(5) |
则管组单位长度受到的浮力为:
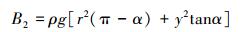
|
(6) |
由图 5可知cosα=y/r。
载荷计算公式为:
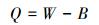
|
(7) |
式中:Q为软管单位长度的静态总体载荷,W为软管单位长度重力,B为软管单位长度受到的海水浮力。

|
(8) |
式中:y < -r为管组全部浸没海水情况,-r≤y≤r为管组漂浮在海面情况。
常用漂浮软管的结构参数为[9]:单根管长12 m,无漂浮层长度5 m,有漂浮层长度7 m,单位长度重力6 000 N,无漂浮层半径0.39 m,漂浮层半径0.53 m。其中海水密度1 030 kg/m3。海平面重力加速度取为10 m/s2。
为了简化计算量,根据管组漂浮载荷公式绘制管组载荷曲线,如图 6所示。

|
| 图 6 管组载荷曲线图 Fig.6 Load curve of the floating hose group |
由图 6可知,在不影响计算精度的情况下,在-r≤y≤r区间内,将管组漂浮载荷等效为线性关系,可令:

|
(9) |
式中:k为-0.53≤y≤0.53时线性段的斜率。
利用图 6中A和B2点的坐标,将载荷公式(8)简化为:
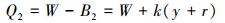
|
(10) |
根据公式(10)将静态总体载荷公式(8)简化为:

|
(11) |
管组在静态情况下受到自身重力以及浮力的作用,将漂浮软管简化为Bernoulli-Euler弹性曲梁,并将软管等效为各向同性材料,利用材料力学中梁理论有[11]:

|
(12) |
对跨度远大于截面高度的梁,上式可作为横力弯曲变形的基本方程,于是有:

|
(13) |
式中:M为管组静态载荷下受到的弯矩,EIz为管组整体抗弯刚度。
在弯矩M作用下,管组受到的剪切力为:

|
(14) |
根据管组受到的剪切力作用,可以得到管组受到的静态总体载荷Q,即:

|
(15) |
在浮筒管汇与首管的接口处,首管浸没在海水中,确保首管加强端刚度过渡,平稳传递浮筒对管组的载荷。
将公式θ=tanθ=y′代入公式(13),结合公式(14)和公式(15),可得一阶微分方程组:

|
(16) |
式中:M为管组的截面弯矩。
4.2 边界条件在浮筒和首管的接口法兰处,浮筒提供给首管施加一个垂向力F0,当管组从主管开始到右端逐渐趋于平衡,重力等于浮力,首管全部浸没在海水中,则首管受浮筒竖直力F0可等效为:

|
(17) |
式中:L0为首管长,0≤x≤xu,Q1=πρgru2;xu≤x≤L0,Q2=πρgrf2。
管组在静水中,首管受到的竖直平面内的弯矩M0取决于首管的参数以及浮筒管汇的倾斜角θ,根据文献[12]给出的计算公式:

|
(18) |
其中

|
(19) |
结合飘浮软管结构参数,利用公式(16)和(17),设定管组边界条件如下:管汇接口距水平面0.5 m,管汇接口倾斜角0.261 67 rad,浮筒弯矩52.4 kN·m,浮筒竖直力-16.19 kN,管组抗弯刚度400 kN·m2。
4.3 方程求解根据管组的边界条件,结合方程(16),推导获得管组在静态载荷作用下,管组轴线在竖直平面上的位移函数:

|
(20) |
根据软管参数和管组边界条件参数,结合管组静态总体载荷公式(11)可得:

|
(21) |
利用位移函数(20)结合静态总体载荷公式(21)拟合漂浮管组形态分布,结果如图 7所示。

|
| 图 7 漂浮管组形态分布图 Fig.7 Morphological distribution of floating hose group |
由图 7可知,当浮筒管汇接口位于水平面以下0.5 m时,首管则完全浸没在海水当中,首管的最大位移为1.2 m,最终在浮力的作用下主管可以全部漂浮在水面上。
同理,利用管组的边界条件,结合方程(16),获得管组在静态载荷作用下,管组轴线在竖直平面上承受的弯矩函数:

|
(22) |
利用管组弯矩函数结合静态总体载荷函数(21)拟合弯矩分布,结果如图 8所示。

|
| 图 8 漂浮管组弯矩图 Fig.8 Bending diagram of floating hose group |
由图 8可知,漂浮管组的静态竖直最大弯矩发生在首管与浮筒管汇的接口处,由计算可得Mmax=M0=52 389.4 N·m。由此可知,海上漂浮管组在首管与浮筒管汇连接的法兰处,容易产生很大的弯矩。因此在设计软管首管时,要注意首管一端加强结构的设计。
4.4 基于ABAQUS有限元模拟利用ABAQUS软件建立了每根12 m,共120 m长的漂浮管组有限元模型。为了简化建模过程,选择wire建模形式,设置管组环形截面。根据材料和环境参数,充分考虑浮筒对管组造成的边界条件影响,获得了管组位移云图(见图 9)和管组截面弯矩云图(见图 10)。

|
| 图 9 漂浮管组位移云图 Fig.9 Morphological distribution of floating hose group |

|
| 图 10 漂浮管组弯矩云图 Fig.10 Bending diagram of floating hose group |
由图 9可知,管组最大位移发生在首管靠近与管汇接口处,最大位移为1.319 m。
由图 10可知,管组最大弯矩发生在首管与浮筒管汇接口处,最大弯矩为53 390 N·m。理论推导与有限元模拟对比如表 1所示。分析表 1数据,2种方法计算的最大位移和最大弯矩误差分别为9.9%和1.9%。
| 对比项目 | 理论计算 | 有限元模拟 |
| 最大位移/m | 1.200 | 1.319 |
| 最大弯矩/(N·m) | 52 389.4 | 53 390.0 |
4.5 差异分析
有限元计算结果与理论计算结果存在一定差异,分析存在差异的原因可能有:
(1) 软管由复合材料组成,复合材料的加工工艺非常复杂,容易产生一定初始缺陷,且缺陷程度目前无法从理论上评估,同时有限元理论计算无法考虑初始材料缺陷及工艺缺陷。
(2) 在理论计算中对软管进行了简化假设,将管组所受载荷进行了线性化处理,在有限元模拟过程中是通过内部参数设置,获得了环境载荷,两者载荷之间存在一定差异。
5 结论与建议(1) 通过对海上漂浮输油管组整体静态性能进行研究,发现作用在管组上的载荷是关于自重、外径以及海水密度的函数。管组在漂浮状态下承受的静态载荷趋近于线性分布,因此,对管组进行前期设计时,可以将静态载荷进行线性化处理。
(2) 通过对管组载荷进行线性化处理,为数值求解管组漂浮形态以及弯矩分布提供了简化的方法,同时缩短了计算时间。
(3) 漂浮管组在静态载荷作用下,最大弯矩发生在浮筒和首管接口法兰处,且最大值为52.4 kN·m,最大弯曲主要取决于软管抗弯刚度、管组与浮筒管汇接口的倾斜角。
(4) 首管相对于主管在竖直平面内发生较大位移,首管的最大位移为1.2 m,即首管发生比较大的弯曲。因此在首管与浮筒连接处需要设计一定的截面刚度过渡结构。
| [1] | GONZALEZ G. Behavior of offloading marine hose submitted to bending[J]. Research Gate, 2014(4): 86–95. |
| [2] | 孟浩龙, 吕庆宏, 李菁信, 等. 海上浮动软管的静态数学模型[J]. 油气储运, 2002, 21(3): 10–12. |
| [3] | 孟浩龙, 吕庆宏, 李菁信, 等. 海上浮动软管的三维静态分析[J]. 海洋工程, 2003, 21(1): 109–112. |
| [4] | XU H, ZHANG C, LUO Y. Analysis of tensile and bending mechanical properties of offshore floating oil hose[J]. Oil & Gas Storage, 2012, 31(4): 279–282. |
| [5] | 王猛, 张捷. 悬链系泊系统中的粘结软管[J]. 海洋工程装备技术, 2015, 2(1): 40–44. |
| [6] | BROWN M J. Mathematical model of a marine hose-string at a buoy[J]. Springer-Verlag, 1992(10): 252–277. |
| [7] | DE ZOYSA A P K. Steady-state analysis of undersea cables[J]. Ocean Engineering, 1978, 5(3): 209–223. DOI: 10.1016/0029-8018(78)90038-0 |
| [8] | PEYROT A H, GOULOIS A M. Analysis of cable structures[J]. Computers & Structures, 1979(10): 805–813. |
| [9] | 张帆, 张世福, 陈畅. 海上漂浮输油软管力学分析研究现状[J]. 自动化与仪器仪表, 2015(11): 15–17. |
| [10] | BROWNL M J, ELLIOTT L. Two-dimensional dynamic analysis of a floating hose string[J]. Applied Ocean Research, 1998, 10(1): 20–23. |
| [11] | 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 1987. |
| [12] | O'DONOGHE T, HALLIWELL A. Floating hose-strings attached to a calm buoy[J]. Offshore Technology, 1988(8): 313–318. |



