0 引言
经典流体力学认为,层流状态时壁面粗糙度对管路压降影响较小[1]。随着附面层理论的发展,人们逐渐认识到壁面粗糙度对管路的压降不可忽略。尤其是高黏性流体[2],壁面粗糙度的变化对附面层影响较大,同时壁面存在孔眼的流场更加复杂,从而导致壁面摩擦压降计算的难度更大。部分学者认为,井筒中充满流体后,壁面孔眼处充填流体代替了原管路,相比原管路壁面粗糙度而言,充填流体后降低了孔眼处的表面粗糙度,从而降低了壁面摩擦压降;壁面孔眼的存在增大了壁面粗糙度和壁面摩擦压降[3-4]。
针对圆管管壁摩阻系数对摩擦压降影响规律的试验研究开展较多[5-15],针对层流摩阻系数也得出了相关的理论模型,但均以清水为试验流体介质,同时试验过程管路孔密较低,是否适用于稠油和孔密较大的星孔筛管仍需通过试验研究进行验证。因此,笔者基于自主研制的室内多相复杂流动装置,开展了多种目数下的防砂筛管阻力系数试验研究,并回归得到了阻力系数模型。
1 试验研究 1.1 试验目的测量稠油条件下不同目数防砂筛管固液两相流动时的流动阻力系数,并基于试验数据,得到阻力系数模型。
1.2 试验装置试验装置主体可分为4大部分:井筒模拟环路段、试验流体供给与控制系统、压降采集及处理系统和固液分离系统。
1.2.1 井筒模拟环路段试验管道采用全尺寸ø139.7 mm(5.5 in)的有机玻璃管,分为3部分:前稳定发展段3.0 m,试验段2.0 m,观察段2.5 m。其中试验段布有螺旋射孔,射孔密度为12孔/m,射孔直径为0.01 m,射孔相位角为45°;试验段前、后各一个测压点,与压力采集系统连接,能够实时测量试验段的压降;试验段前、后各分布2个取样点。稳流段和观察段分别与试验段用法兰连接。
1.2.2 试验流体供给与控制系统该系统主要包括2台螺杆泵以及2个控制箱、蓄水罐、储油罐,其主要功能是给试验管路提供流体,以及控制流体流量和流体速度,同时提供一定压力使之通过试验管路。蓄水罐和储油罐是为了使流体实现循环利用。
1.2.3 压降采集及处理系统该系统主要包括测压表、1台装有压降采集和处理软件的电脑。试验段两端的测压点压力通过压差传感器以一定的频率连续输出到接收端,并在电脑上以直观的曲线表示出来,并且可以通过处理软件直接读取并导出保存。
1.2.4 分离系统该系统主要作用是过滤试验过程中的砂粒,使液相实现循环,主要包括1个沉砂箱、1个大圆柱罐、1台螺杆泵以及1台离心泵。
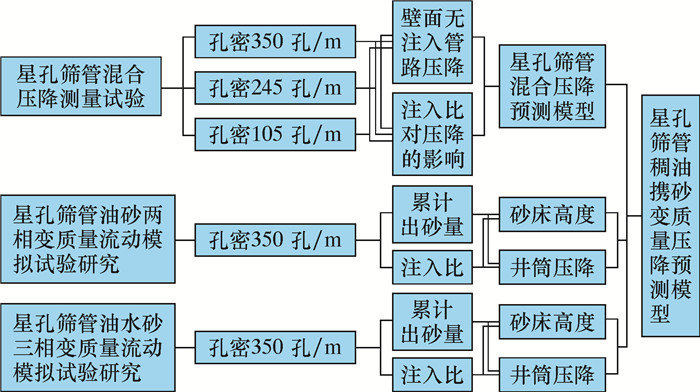
1.3 试验方案为了准确模拟变质量流动时不同敏感参数对流动规律的影响,试验共分为以下3部分(具体试验流程如图 1所示)。
|
| 图 1 变质量流动模拟试验流程图 Fig.1 Flow chart of variable mass flow simulation test |
1.3.1 星孔筛管混合压降测量试验
通过改变管路主流流量和壁面入流流量,测量不同孔密时试验管路压降变化,以得到孔密和注入比对井筒压降的影响规律,并得到单相变质量流动压降预测模型。
1.3.2 星孔筛管油砂两相变质量流动规律模拟试验由于此时引入了壁面入流,难以使主流和壁面入流的含砂浓度保持一致,综合考虑地层出砂时,地层游离砂和骨架砂总数一定,故此处引入地层累计出砂量,即在每次试验前,主流管和入流管分别配比成相同质量浓度、同一粒径配比的砂粒,用以模拟一定地层累积出砂量,观察砂床高度分布及压降变化规律。
1.3.3 星孔筛管油水砂三相变质量流动规律模拟试验在油砂两相变质量流动规律模拟试验基础上,模拟不同含水质量分数(10%、30%、50%、70%和90%)条件下油水砂三相变质量流动压降和流型的变化规律。
2 无壁面入流试验数据分析及模型推导 2.1 模型假设(1) 系统处于等温流动状态,与外界无能量交换。
(2) 星孔筛管孔为圆形,且分布均匀。
(3) 液相流体为不可压缩牛顿流体。
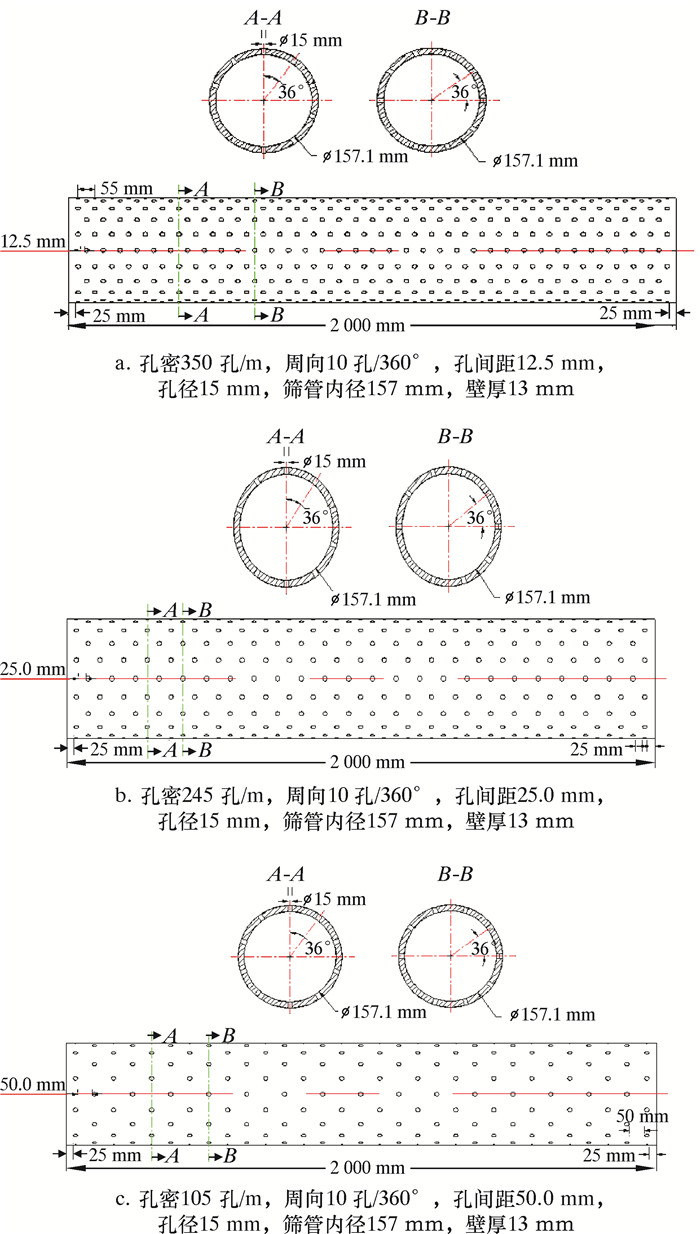
2.2 数据分析及模型推导由于稠油油藏产量较低,所以其在井筒中的流动均为层流流动,相对于前人针对圆管壁面层流流动规律开展的试验研究而言,由于星孔筛管壁面入流孔孔密较大,对层流边界层影响较大,所以通过试验研究分析了不同孔密条件下星孔筛管对圆管粗糙度的影响规律,进行了无壁面入流条件下(通过星孔筛管模拟管路外包裹保鲜膜,阻绝了壁面环空流体与井筒内流体的掺混,防止环空流体对管内边界层的干扰)的摩擦压降研究。试验时分别模拟了3种孔密(350孔/m、245孔/m及105孔/m)的星孔筛管,孔眼直径均为15 mm,管路内径157 mm,其中350孔/m试验管路按照实际ø177.8 mm(7 in)苍南星孔筛管1:1设计,如图 2所示。
|
| 图 2 孔筛管模拟试验管路设计图 Fig.2 Pipeline design of simulation test of astropyle sand control screen |
为了模拟稠油油藏在低产量条件下井筒复杂流动规律,试验时管路主流量流速较低(0.01~0.12 m/s),即产量在16.7~200.0 m3/d之间。由于白油黏度受温度影响较大,故试验过程中需要实时测量白油的黏度。
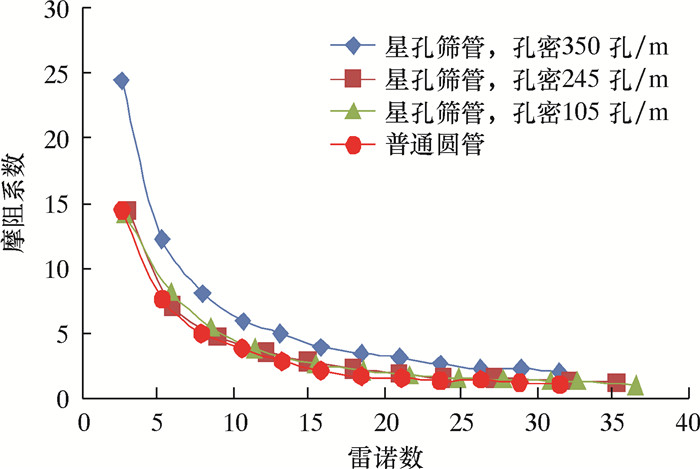
不同孔密筛管雷诺数与摩擦阻力系数的关系曲线如图 3所示。从图可见,星孔筛管孔密对井筒摩擦影响较大,比普通圆管摩擦压降降低了约40%。分析原因:相对圆管时的粗糙度而言,星孔孔眼位置由白油代替了有机玻璃管,减小了管壁的摩擦因数;同时由于流速较低,在星孔位置形成的涡流较小,能量耗散较少,故降低了管壁摩擦压降。当井筒流速较低时,不同孔密之间的摩擦压降相差较小,但不能忽略。总体规律为:随着孔密的增大,摩擦压降逐渐增大。
|
| 图 3 不同孔密筛管雷诺数与摩阻系数关系曲线 Fig.3 The relation curve of Reynolds number and friction resistance coefficient of sand control screen with different hole densities |
基于试验数据,回归得到不同孔密对摩阻系数的影响规律,也即摩阻系数预测模型:
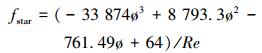
|
(1) |
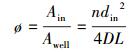
|
(2) |
式中:fstar为星孔筛管摩阻系数;ø为注入面积之比;Re为主井筒雷诺数;Ain为壁面入流面积,m2;Awell为主井筒过流面积,m2;n为星孔筛管孔密,孔/m;din为星孔筛管入流孔直径,m;D为主井筒直径,m。
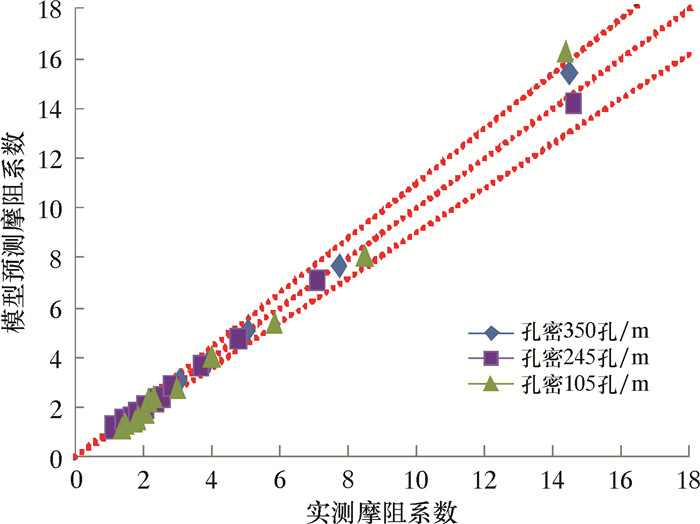
如图 4所示,摩阻系数预测模型的最大相对误为13.8%,平均相对误差2.47%,满足工程需要。
|
| 图 4 模型预测摩阻系数与实测摩阻系数对比 Fig.4 Comparison between the friction coefficient predicted by the model and the measured friction coefficient |
3 有壁面入流试验数据分析及模型推导 3.1 模型假设
(1) 系统处于等温流动状态,与外界没有能量交换。
(2) 星孔筛管孔为圆形,且分布均匀。
(3) 液相流体为不可压缩牛顿流体。
(4) 壁面入流为均匀注入。
3.2 数据分析及模型推导为了进一步研究不同注入比对单相变质量流动压降的影响规律,分别开展了不同孔密条件下注入比(定义壁面入流流量与主流流量之比)对星孔筛管井筒压降影响规律的试验研究。
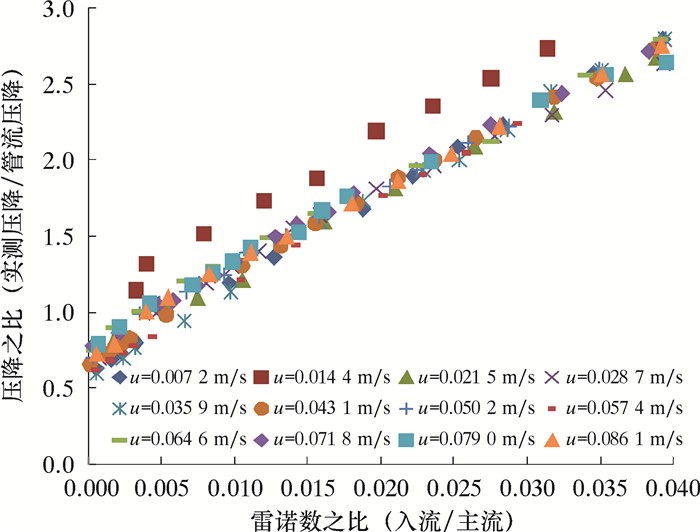
通过试验研究发现,随着注入比的增大,压降逐渐增大。当井筒主流流速较低时,注入流量对井筒压降的影响较小,随着井筒主流流速的增大,注入比对井筒压降影响逐渐增大(如图 5所示)。
|
| 图 5 雷诺数之比与井筒变质量流动压降关系曲线(350孔/m) Fig.5 The relation curve of the Reynolds number ratio and wellbore variable mass flow pressure drop (350 holes/m) |
为了进一步分析注入比对井筒压降的影响规律,引入L.B.OUYANG提出的入流雷诺数[16]:
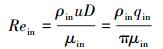
|
(3) |
式中:Rein为壁面入流雷诺数;ρin为壁面入流流体密度,kg/m3;u为壁面入流流速,m/s;μin为壁面入流流体黏度,Pa·s;D为井筒内径,m;qin为壁面入流流量,m3/s。
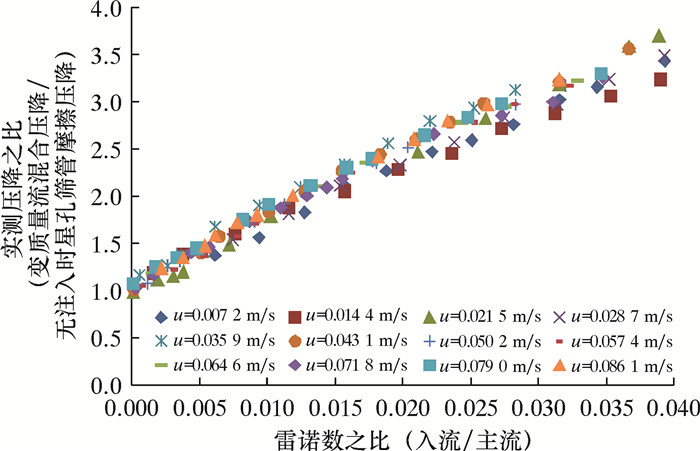
定义Rein/Rem为雷诺数之比,即壁面入流雷诺数与主流雷诺数之比。雷诺数之比与井筒变质量流动压降之比的关系曲线如图 6所示。由图可以看出,不同井筒流速下均存在临界雷诺数之比,当雷诺数之比小于临界雷诺数之比时,井筒变质量流动压降小于普通圆管摩擦压降;当雷诺数之比大于该临界值时,井筒变质量流压降大于普通圆管摩擦压降。不同注入比变质量流动时实测压降(包含摩擦压降、加速压降和混合压降)与无注入时星孔筛管摩擦压降均落在同一直线上[17]。
|
| 图 6 雷诺数之比与井筒变质量流动压降之比关系曲线(350孔/m) Fig.6 The relation curve of the Reynolds number ratio and wellbore variable mass flow pressure drop ratio (350 holes/m) |
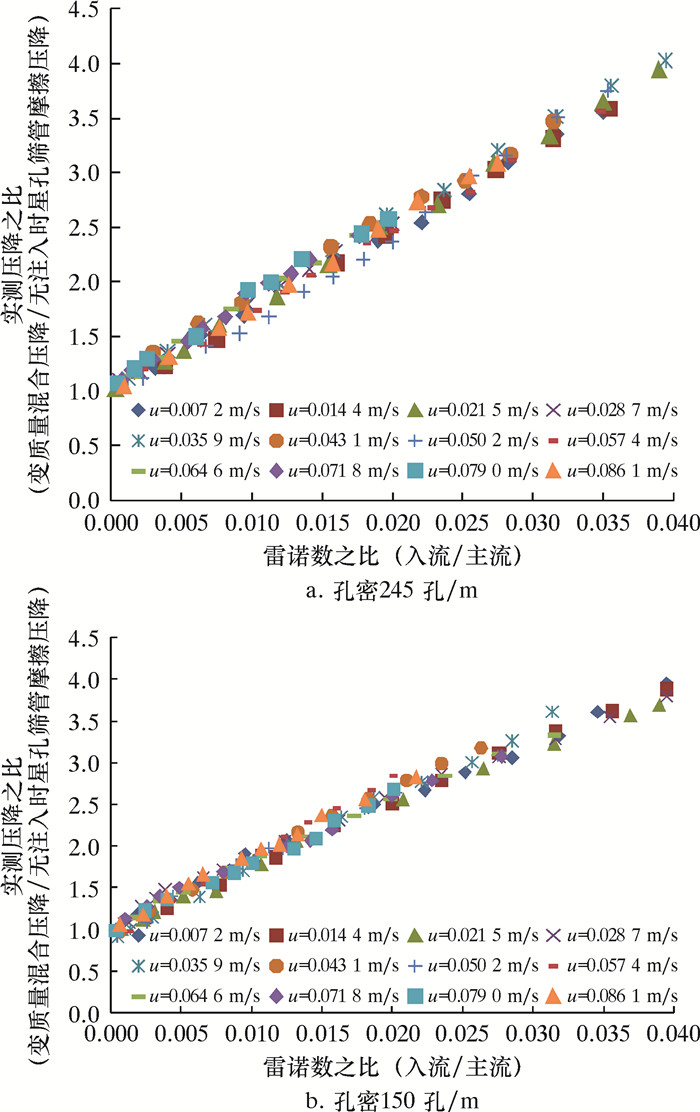
为了更好地验证试验结果,在孔密350孔/m星孔筛管试验研究的基础上,分别研究了245和105孔/m 2种孔密试验段在不同注入比下的实测压降,如图 7所示。
|
| 图 7 雷诺数之比与井筒变质量流动压降的关系曲线 Fig.7 The relation curve of the Reynolds number ratio and wellbore variable mass flow pressure drop |
由图 7可知,不同孔密时,变质量流混合压降与无注入时星孔筛管摩擦压降之比与雷诺数之比均成线性关系,即:
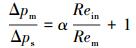
|
(4) |
式中:Δpm为变质量流动压降,Pa;Δps为无壁面入流时星孔筛管压降,Pa;α为修正系数。
分析图 6和图 7可知,不同孔密下式(4)斜率不同,但随着孔密的降低,斜率逐渐增大,通过数学回归可得:
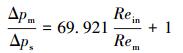
|
(5) |
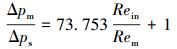
|
(6) |
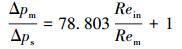
|
(7) |
由式(5)~式(7)可知,当星孔筛管孔密分别为350、245和105孔/m时,式(4)中修正系数α分别为69.921、73.753和78.803(平均相对误差分别为3.72%、3.00%和3.27%,最大相对误差分别为15.94%、12.95%和11.67%。),即随着孔密的增大,雷诺数之比对变质量流动压降的影响逐渐减小。分析可知,随着孔密的逐渐增大,孔眼内流体平均流速逐渐减小,对主流的影响逐渐减小;当孔眼密度趋于无穷大时,即形成壁面均匀渗流,此时对变质量流动压降的影响最小。对修正系数进行数学回归可得:
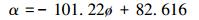
|
(8) |
联合公式(1)、(2)、(4)和(8)即可得到不同孔密星孔筛管单相变质量流动压降预测模型:
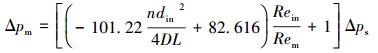
|
(9) |
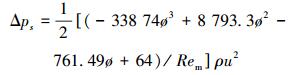
|
(10) |
式中:Δpm为星孔筛管总压降,Pa/m; Δps为无壁面入流时星孔筛管压降,Pa;L为井筒长度,m。
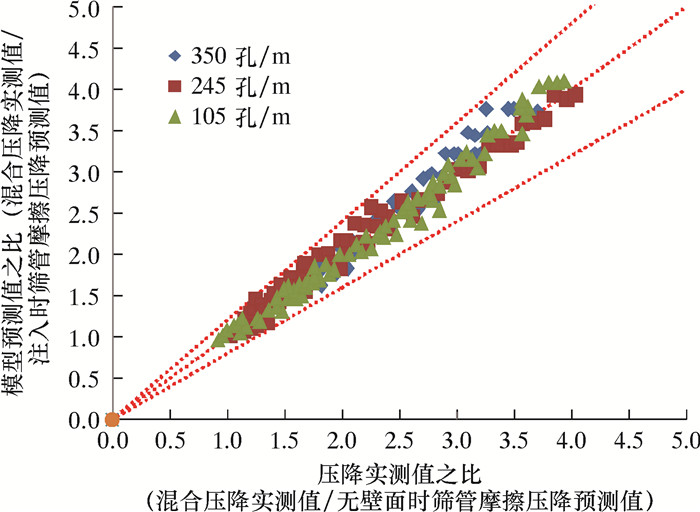
上述模型解决了稠油携砂条件下,低产量、高密度星孔筛管变质量流动压降计算困难的问题。模型预测值与实测值对比如图 8所示。与试验结果相比,模型的平均相对误差为8.33%,最大相对误差为17.94%,适合工程应用。这为下一步固液两相变质量流动研究奠定了理论基础。
|
| 图 8 模型预测值与实测值对比图 Fig.8 Comparison of model predictions and measured values |
4 结论
(1) 壁面无流体注入,当井筒流速较低时,不同孔密之间的摩擦压降相差较小,但是不能忽略,总体规律为:随着孔密的增大,摩擦压降逐渐增大。
(2) 壁面有流体注入,不同井筒流速均存在临界雷诺数之比。当雷诺数之比小于临界雷诺数之比时,井筒变质量流压降小于普通圆管摩擦压降;当雷诺数之比大于该临界值时,井筒变质量流压降大于普通圆管摩擦压降。
(3) 建立的防砂筛管摩阻系数模型对于准确预测及优化单井产能,实现单井效益最大化有重要意义。
(4) 建立的高黏度低雷诺数条件下星孔筛管单相变质量流动压降模型,可解决稠油携砂条件下低产量、高密度星孔筛管变质量流动压降计算困难的问题,并且相对误差较小,具有较高的工程应用价值。
| [1] | 袁恩熙. 工程流体力学[M]. 北京: 石油工业出版社, 2005: 109-127. |
| [2] | 郭永怀. 边界层理论讲义[M]. 北京: 中国科学技术大学出版社, 2008: 18-49. |
| [3] | TELEVANTOS Y, SHOOK C, CARLETON A, et al. Flow of slurries of coarse particles at high solids concentrations[J]. Canadian Journal of Chemical Engineering, 1979, 57(3): 255–262. |
| [4] | MOODY L F. An approximate formula for pipe friction factors[J]. Trans. ASME, 1947, 69: 1005–1006. |
| [5] | 王小秋, 徐静, 汪志明. 水平井筒变质量流动规律的研究进展[J]. 天然气工业, 2005, 25(4): 92–94. |
| [6] | 王宝和, 王喜忠. 计算球形颗粒自由沉降速度的一种新方法[J]. 粉体技术, 1996, 2(2): 30–39. |
| [7] | 李爱芬, 王士虎, 王文玲. 地层砂粒在液体中的沉降规律研究[J]. 油气地质与采收率, 2001, 8(1): 70–73. |
| [8] | 李蘅, 李鹏程, 韩文亮. 垂直管粗颗粒水力提升不稳定流数值模拟[J]. 有色金属工程, 2003, 55(3): 109–111. |
| [9] | 岳雷, 李学广, 李秀英, 等. 出砂抽油井合理产量的确定[J]. 油气田地面工程, 2004, 23(1): 55–56. |
| [10] | 董长银, 武龙, 王爱萍, 等. 基于平衡流速的水平井砾石充填α波砂床平衡高度预测与试验[J]. 中国石油大学学报(自然科学版), 2009, 33(5): 80–83, 88. |
| [11] | 钱宁, 万兆惠. 泥沙运动力学[M]. 北京: 科学出版社: 139-148. |
| [12] | RICHARDSON J F, ZAKI W N. Sedimentation and fluidization[J]. Part Ⅰ, Trans Inst. Chem. Engrs., 1954, 32(1): 35–53. |
| [13] | 郭慕孙, 庄一安. 流态化:垂直系统中均匀球体和流体的运动[M]. 北京: 科学出版社, 1963: 95-99. |
| [14] | 沙玉清. 泥沙运动学引论[M]. 北京: 中国工业出版社, 1965: 300-305. |
| [15] | 夏震寰, 汪岗. 无黏性均质颗粒在细颗粒悬浮液中的沉降[J]. 泥沙研究, 1982(1): 16–25. |
| [16] | OUYANG L B, AZIZ K. A homogeneous model for gas-liquid flow in horizontal wells[J]. Journal of Petroleum Science and Engineering, 2000, 27(3): 119–128. |
| [17] | SCHULKES R M S M, UTVIK O H. Pressure drop in a perforated pipe with radial inflow:Single-phase flow[J]. SPE Journal, 1998, 3(1): 77–85. DOI: 10.2118/38448-PA |




