2. 山东胜利石油装备产业技术研究院
2. Shandong Shengli Petroleum Equipment Industrial Research Institute
0 引言
为提高机械钻速,降低钻井成本[1-3],有关科研人员对各种冲击破岩及旋冲破岩进行了研究。现有技术大多是通过设计各种冲击器,利用轴向冲击以及PDC钻头的剪切作用来进行高效破岩[4-9]。但是过度的轴向力会造成PDC钻头剪切力失效,达不到较好的破岩效果,且会产生黏滑和卡钻现象[10-11]。为了消除钻头的这种现象,提高钻头的破岩效率,冲击钻井技术得到了飞速发展[12-13]。
笔者针对现有技术之不足,设计了一种新型扭振冲击工具。在对该工具进行结构设计及工作原理介绍的基础上,分析了工具的工作特性,建立了撞击发生器偏心环对传动轴的撞击时间模型,研究了撞击时间与流量和频率间的关系,以期为新型扭振冲击工具的理论研究和现场应用提供借鉴。
1 技术分析 1.1 结构新型扭振冲击工具主要由金属马达总成、涡轮马达总成、撞击发生装置总成以及钻头盒子组成,如图 1所示。其中,金属马达总成由金属马达定子、金属马达定子上盖、定子下盖、防掉帽、轴承、轴承端盖、金属马达转子、高低压区隔离棒及长销组成;涡轮马达总成由涡轮马达定子、涡轮马达转子、涡轮马达传动轴、轴承以及平键组成;撞击发生装置总成由涡轮马达传动轴、传动销、花键、内花键传动块、偏心环、撞击发生装置传动轴以及轴承组成;钻头盒子由定位挡圈、盒子及轴承组成。

|
| 图 1 新型扭振冲击工具结构示意图 Fig.1 Structural schematic of a novel torsional vibration tool 1—防掉帽;2—金属马达定子上盖;3—金属马达转子;4—金属马达定子;5—金属马达隔离棒;6—涡轮马达定子;7—内花键传动块;8—撞击发生器传动轴;9—金属马达定子下盖;10—滑动轴承;11—钻头盒;12—定位挡圈;13—传动销;14—撞击发生器偏心环;15—花键;16—平键;17—马达转子;18—马达传动轴。 |
1.2 工作原理
一部分钻井液流入金属马达定子上盖边缘的通道,进入金属马达定子与转子之间的环空,金属马达隔离棒在钻井液的压力下把环空分割成高压区和低压区,当高压区的压力升到一定值时,金属马达顺时针转动,并带动撞击发生器外筒、花键传动块以及撞击发生器传动轴转动,随着金属马达转子的不断旋转,低压区的空间不断减小,被挤出的钻井液一直向下流动,最终流入到钻头中。另一部分钻井液进入金属马达转子内部,进而流入到涡轮中,带动涡轮传动轴、撞击发生器偏心环旋转,并且与金属马达转子流出的钻井液汇合,流向钻头。由于涡轮马达的转速高于金属马达转速,所以撞击发生器偏心环的转速也会高于撞击发生器传动轴的转速。在某个时刻,撞击发生器偏心环的锤面与撞击发生器传动轴的铁砧发生周向碰撞产生扭转振动,并通过撞击发生器传动轴将其传递到下接头,两者碰撞完之后,撞击锤面与铁砧的碰撞面分离,进行下一次撞击,这样就会使两者之间不断地出现周期性的周向碰撞,形成高频单向的周向冲击。
1.3 技术特点(1) 新型扭振冲击工具的撞击发生器偏心环对撞击发生器传动轴的冲击作用是主要动力执行机构,这种运动方式突破了传统的牙轮钻头和PDC钻头常规的钻井方法,可为PDC钻头提供超高转速,使PDC钻头能更加高效地钻进岩石,有效提高了PDC钻头的机械钻速,降低了钻井成本。
(2) 该工具形成了高频率、均匀稳定的机械冲击能量和旋转动能,使钻头和井底能够始终保持连续的高频切削,提高钻头剪切效率,消除PDC钻头运动时可能出现的有害振动,有利于消除黏滑现象。
(3) 该工具的使用使PDC钻头在软硬交错不均质夹层中,特别是在塑性岩层中能够发挥良好的作用,扩大了PDC钻头的使用范围。
2 工作特性分析根据新型扭振冲击工具的工作原理可知,撞击发生器偏心环对撞击发生器传动轴的冲击作用是该工具的主要动力来源,而此动力来源又主要依靠钻井液的流量进行驱动;同时,撞击频率和撞击时间又决定了该工具的工作性能以及破岩效率。因此,流量的变化对撞击时间和撞击频率有着至关重要的影响。通过提高流量来提高该工具的破岩效率以及机械钻速具有重要意义;同样,又可以根据流量的变化来确定金属马达和涡轮马达内流量的变化,并以此来确定流道宽度、涡轮马达转子半径以及环空截面积等参数。
通过以上分析可知,撞击发生器的偏心是结构设计的关键部件,其具体结构如图 2所示。

|
| 图 2 关键部件结构示意图 Fig.2 Structural schematic of the key components 1—轴承;2—短销;3—撞击发生器传动轴;4—撞击发生器偏心环。 |
根据弹塑性力学以及碰撞原理可知,两者的冲击实际上是一个碰撞过程,将撞击发生器偏心环和传动轴进行简化并做如下假设:撞击发生器偏心环和传动轴的材料均匀、各向同性且完全弹性,接触表面的摩擦力及半径大小可以忽略不计,并且表面是理想的光滑表面。建立如图 3所示的理论模型。

|
| 图 3 理论模型 Fig.3 Theoretical model |
设撞击发生器偏心环和传动轴为对心碰撞,碰撞分2个过程:碰撞开始时,撞击发生器偏心环和传动轴由于局部变形而逐步缩短,相对速度减小到0,此时达到了压缩的最大状态,随后两者逐步恢复变形,速度逐渐增大,直到相对速度达到最大值vr0。两者接触压力p由0增加到最大值,又逐步减小到0,该接触压力的变化与两者之间距离δ的变化有关,因此可得:

|
(1) |
其中
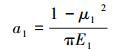
|
(2) |

|
(3) |
式中:R1、R2分别为撞击发生器偏心环和传动轴的半径,m;E1、E2分别为撞击发生器偏心环和传动轴的弹性模量,MPa;μ1、μ2分别为撞击发生器偏心环和传动轴的泊松比。
2个平面碰撞时,将式(1)简化为:

|
(4) |
将公式(4)化简可得:
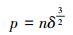
|
(5) |
其中
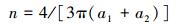
|
(6) |
2平面碰撞时,接触压力p使撞击发生器偏心环做减速运动,撞击发生器传动轴做加速运动,二者的线速度分别为vp和vc,根据牛顿第二定律,建立运动微分方程:
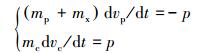
|
(7) |
式中:mc、mp分别为撞击发生器传动轴和偏心环的质量,kg;mx为传动销的质量,kg;vp、vc分别为撞击发生器偏心环和传动轴的线速度,m/s。
撞击发生器偏心环与传动轴的相对速度vr应该与两者之间的压缩距离对时间t的微分相等,即有:

|
(8) |
将式(8)两边分别对时间求导得:

|
(9) |
其中

|
(10) |
将式(5)代入式(9)可得:

|
(11) |
将式(11)两边乘以dδ得:

|
(12) |
撞击发生器偏心环与传动轴开始碰撞时其压缩距离为0,相对速度为vro,当压缩距离为δ时,其相对速度为vr=dδ/dt,对式(12)进行积分得:

|
(13) |
当压缩到终点时相对速度为0,则由式(13)可以计算出撞击发生器偏心环与传动轴之间的最大压缩距离为:

|
(14) |
将式(14)代入式(5)得:

|
(15) |
对式(13)取微分得到压缩阶段所需时间为:

|
(16) |
令δ/δmax=x,在碰撞开始时,t=0,δ=0,故x=0;到达压缩结束t1时刻,δ=δmax,x=1,因此,对式(16)积分得到:

|
(17) |
令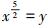
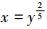
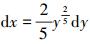

|
(18) |
通过查β函数表,并化简可得:

|
(19) |
对于完全弹性碰撞的撞击发生器偏心环与传动轴来说,其恢复原有状态所需时间与碰撞压缩所需时间相等,因此,撞击发生器偏心环与传动轴的整个碰撞时间为:

|
(20) |
由式(20)及式(8)可知,撞击发生器偏心环与传动轴的整个撞击时间与两者的相对速度vro以及偏心环的线速度vp、传动轴的线速度vc有密切关系,而由该工具的结构及工作原理可得:

|
(21) |
式中:ωp为撞击发生器偏心环角速度,rad/s;ωc为撞击发生器传动轴角速度,rad/s;vz为涡轮传动轴线速度,m/s;vw为涡轮马达转子线速度,m/s;Rp为撞击发生器偏心环半径,m;Rz为涡轮马达传动轴半径,m;Rw为涡轮马达转子半径,m;vza为金属马达转子线速度,m/s, Rc为撞击发生装置传动轴半径,m;Rza为金属马达转子半径,m。
金属马达线速度的求解公式为:

|
(22) |
式中:Q为流经金属马达内流体的流量,L/s;S为金属马达转子与定子内壁之间的环空截面积,m2;l为金属马达转子工作长度,m;ηv为金属马达容积效率,取0.92。
涡轮马达的线速度求解公式为:

|
(23) |
式中:Qw为流经涡轮马达内流体的流量,m3/s;α1k为涡轮定子叶片出口角,rad;B为流道的宽度,m;φ为叶片厚度影响的断面收缩系数,取0.9。
由式(21)~式(23)可求得:

|
(24) |
根据新型扭振冲击的结构设计及试验数据可知,流经金属马达内流体的流量是流经涡轮马达内流体流量的3.5倍,将式(24)代入(20)可得:

|
(25) |
根据扭振冲击工具的工作原理及工作特性进行算例分析,将设计及现场的真实参数代入计算方法进行求解与分析。其中,撞击发生器偏心环的弹性模量和传动轴的弹性模量均为210 GPa,偏心环传动轴的泊松比为0.27,传动轴的质量为3.40 kg,偏心环的质量为1.16 kg,流道宽度为0.5 m,涡轮马达转子半径为0.03 m,涡轮定子叶片出口角为0.17 rad,金属马达转子与定子内壁之间的环空截面积为27.07×10-4 m2,金属马达转子工作长度为0.95 m。求得撞击发生器偏心环与传动轴相互作用下撞击时间与流量和撞击频率的关系曲线,如图 4和图 5所示。由图可知,随着流量增加,撞击发生器偏心环与传动轴的撞击时间缩短,即流量越大,金属马达与涡轮马达的转速越高,传递给钻头的扭矩越大,钻头的破岩效率和机械钻速越高。当流量增加到40 L/s时,偏心环与传动轴撞击时间约为1×10-4 s,撞击频率最大值将达到11 kHz。因此,在不影响现场施工安全的情况下,应尽量提高钻井液排量,以获得较高的破岩效率和机械钻速。

|
| 图 4 撞击时间与流量关系曲线 Fig.4 The relationship of impact time and flow rate |

|
| 图 5 撞击时间与频率关系曲线 Fig.5 The relationship of impact time and frequency |
4 结束语
现有冲击破岩及旋冲破岩技术大多利用轴向冲击及PDC钻头的剪切作用来进行高效破岩,但是过度的轴向力会造成PDC钻头剪切力的失效,且会发生黏滑和卡钻现象。鉴于此,笔者设计了新型扭振冲击工具。对新型扭振冲击工具的运动特性进行分析,建立了撞击发生器偏心环对传动轴的撞击时间模型,并对撞击时间与流量和频率之间的关系进行研究。分析结果表明:流量越大,撞击发生器偏心环与传动轴相互作用下的撞击时间越短,撞击频率越高,钻头冲击岩石的速度越快,越有利于提高钻头的破岩效率和机械钻速。
| [1] | 李梦, 苏义脑, 孙友宏, 等. 高胎体仿生异型齿孕镶金刚石钻头[J]. 吉林大学学报(工学版), 2016, 46(5): 1540–1545. |
| [2] | 杨传书, 张好林, 肖莉. 自动化钻井关键技术进展与发展趋势[J]. 石油机械, 2017, 45(5): 10–17. |
| [3] | 江同文, 滕学清, 杨向同. 塔里木盆地克深8超深超高压裂缝性致密砂岩气藏快速、高效建产配套技术[J]. 天然气工业, 2016, 36(10): 1–9. |
| [4] | WILSON A. Hydraulic percussion drilling system boosts rate of penetration, lowers cost[J]. Journal of Petroleum Technology, 2015, 67(12): 79–80. DOI: 10.2118/1215-0079-JPT |
| [5] | 李玮, 纪照生, 董智煜, 等. 基于重整化方法的冲击载荷下岩石振动分析[J]. 振动与冲击, 2016, 35(16): 49–54. |
| [6] | AZAR M, LONG W, WHITE A, et al. A new approach to fixed cutter bits[J]. Oilfield Review, 2015, 27(2): 30–35. |
| [7] | 田家林, 杨志, 付传红, 等. 高频微幅冲击振动作用下岩石破碎行为计算方法[J]. 吉林大学学报(地球科学版), 2015, 45(6): 1809–1866. |
| [8] | 祝效华, 汤历平, 童华. 高频扭转冲击钻进的减振与提速机理研究[J]. 振动与冲击, 2012, 31(20): 75–78. |
| [9] | 雷鹏, 倪红坚, 王瑞和, 等. 自激振荡式旋转冲击钻井工具水力元件性能分析与优化[J]. 振动与冲击, 2014, 33(9): 175–180. |
| [10] | TANG L, ZHU X, SHI C, et al. Study of the influences of rotary table speed on stick-slip vibration of the drilling system[J]. Petroleum, 2015, 1(4): 382–387. DOI: 10.1016/j.petlm.2015.10.004 |
| [11] | 吕苗荣, 沈诗刚. 钻柱粘滑振动动力学研究[J]. 西南石油大学学报(自然科学版), 2014, 36(6): 150–159. DOI: 10.11885/j.issn.1674-5086.2013.02.22.02 |
| [12] | MISHRA S, YADAVA V. Modeling and optimization of laser beam percussion drilling of thin aluminum sheet[J]. Optics & Laser Technology, 2013, 48: 461–474. |
| [13] | 赵健, 韩烈祥, 徐依吉, 等. 粒子冲击钻井技术理论与现场试验[J]. 天然气工业, 2014, 34(8): 102–107. |



