2. 国家油气钻井装备工程技术研究中心
2. National Engineering Research Center for Oil and Gas Drilling Equipment
0 引言
近年来,随着集约化和工厂化钻井技术的不断发展,越来越多的油田开发时采用近距离直线状、网状或者环状的井口布置,为了满足此种作业形式,步进移运装置应运而生[1]。步进移运装置的采用可极大地减少钻机拆卸与安装准备的时间,缩短钻机转场时间,提高作业效率。步进移运装置具有操作简单和移运快速的特点,能够实现钻机纵向、横向、斜向、沿弧线转向及零半径转向的移运作业。因此在钻机步进移运装置的设计中,转向设计是一个重要环节,零半径转向更是钻机转向设计的一大难点。
目前,国内步进移运装置技术的发展还不够成熟,仅能够实现钻机的横向、纵向和斜向移运[2-5],在钻机整体的零半径转向功能的实现上还有很大的发展空间[6]。近年来,宝鸡石油机械有限责任公司研制出一种新型步进移运装置,该装置可实现零半径转向功能。笔者对其原理进行分析,同时对不规则四边形结构进行分析和验证,从而为全方位步进移运装置的设计与研发提供理论支持和设计参考。
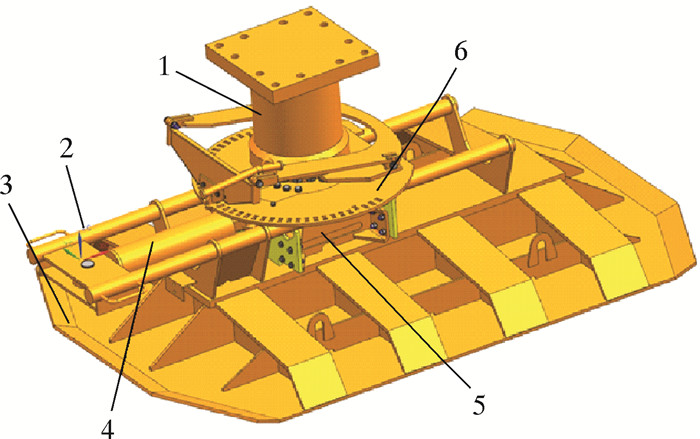
1 步进移运装置技术分析步进移运装置结构如图 1所示。该装置主要由顶升油缸、导向杆、滑靴、滚轮小车、分度盘和推力油缸等组成。每套钻机一般配备有4组步进移动装置,分别布置在钻机底座基座梁四角。移动装置以液压为系统动力源,通过控制阀实现协调同步工作。
|
| 图 1 步进移运装置结构简图 Fig.1 Structural schematic of the walking device 1—顶升油缸;2—导向杆;3—滑靴;4—推力油缸;5—滚轮小车;6—分度盘。 |
步进装置在进行零半径转向及沿圆弧转向时分度盘的位置情况如图 2所示。

|
| 图 2 零半径转向时分度盘位置图 Fig.2 Compass rose position during zero radius steering |
当钻机进行零半径转向时,只需在滚轮小车和滑靴悬空的情况下,提起旋转臂上的连接板,旋转滚轮小车与滑靴到指定角度,再将连接板与分度盘固定,即可使钻机旋转。每当完成一个步进过程,在旋转臂与滑靴上导向杆的作用下,滑靴会在被提起的时候自动完成复位动作,从而进行下一个步进过程直至完成旋转。
2 零半径转向原理分析步进装置的零半径转向过程类似于汽车的全轮转向,旋转过程符合阿克曼转向原理[7-8]。由图 2以及步进移运工作原理可知,钻机在进行零半径转向时,在启动初始阶段,只受到顶升液压缸竖直方向的力与推力液压缸沿着滑靴导向杆方向的力。通过对钻机实际尺寸的测量与工作过程分析,钻机移运系统可简化为一个矩形结构。以步进装置工作空间建立坐标系,则其旋转过程只在XY平面中进行,因此可以忽略Z轴方向的作用力,即忽略步进移运装置顶升液压缸对钻机的作用力。将步进旋转过程视为一个连续过程,其结构与作用力关系可简化为如图 3的形式,该结构形式为步进移运旋转工况下的典型形式。
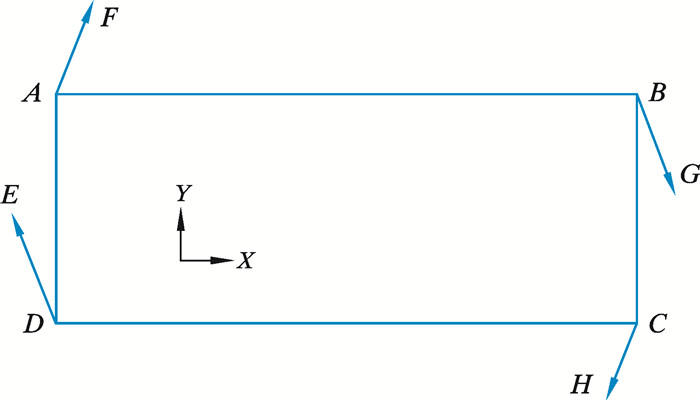
|
| 图 3 步进移运装置数学模型 Fig.3 Mathematical model for walking device |
图 3中矩形ABCD表示钻机整体,可视为一个刚体,矩形4个顶点A、B、C和D分别表示4组步进移运装置所在位置,4条线段AF、BG、CH和DE分别表示步进移运装置推力液压缸的推力方向。
步进移运装置零半径转向过程的实现可看作是刚体沿着线段AF、BG、CH和DE 4个方向在推力液压缸推力作用下,刚体自身进行旋转的过程。因此,需要对4个推力液压缸推力的方向及大小进行确定。
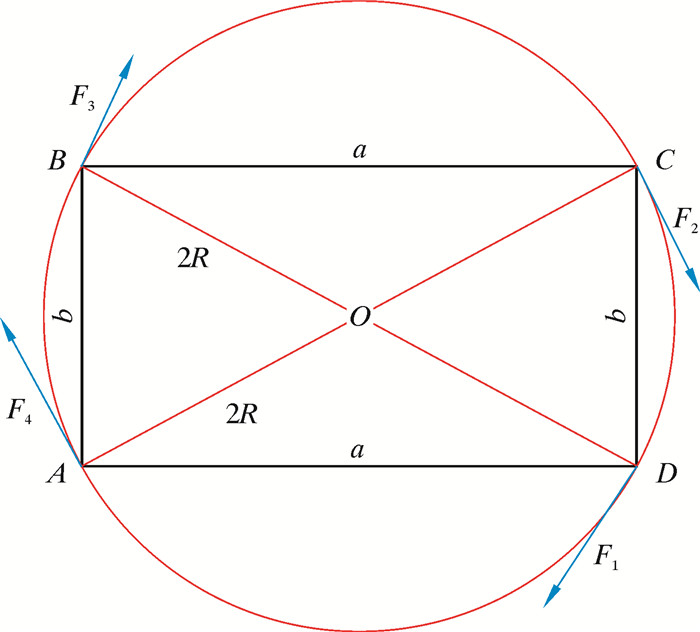
2.1 作用力方向的确定在典型步进移运装置零半径转向结构形式下,其作用力方向如图 4所示。若A、B、C、D 4点绕同一瞬时转动中心O进行旋转,则A、B、C、D 4个顶点的运行轨迹必然为矩形ABCD的外接圆。由于步进移运装置工作速度较低,转向强度较小,所以忽略A、B、C、D 4点处的侧偏影响,则施加在4点上的作用力的垂直平面都相交于同一直线上,交点即瞬时旋转中心O[9]。由图 3可知,步进移运装置零半径旋转时瞬时旋转中心与矩形ABCD几何中心重合,A、C 2点,B、D 2点分别构成一个力偶,则4个作用力方向必然沿着圆的切线方向,合力大小为0,如图 4所示,4个合力形成一个力偶系,在矩形结构受力平衡的同时给矩形一个以O点为圆心的扭矩,实现结构的零半径转向。
|
| 图 4 矩形作用力方向 Fig.4 The direction of rectangular force |
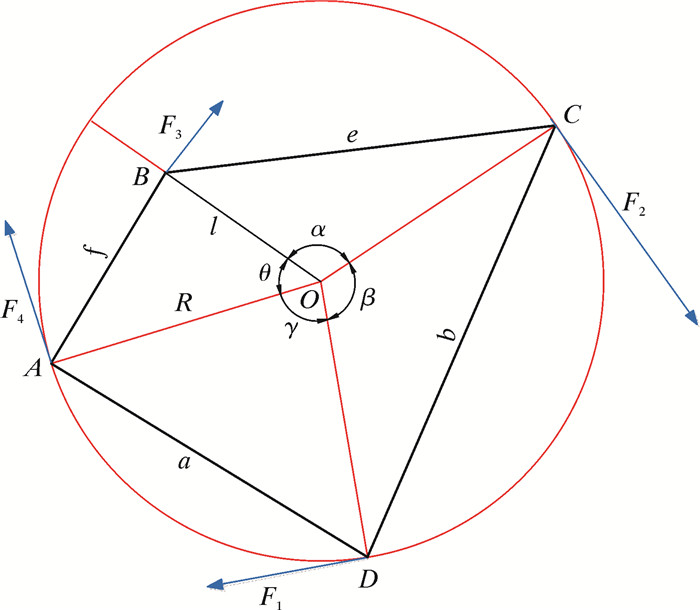
在典型结构步进装置受力分析的基础上,对该结构零半径转向原理进行推广,得出在非对称四边形结构下步进移运装置实现零半径转向时作用力的施加方向。由定理“不共线的3点构成一个圆”可知,四边形ABCD中的3个顶点必然在一个圆上。假设A、C、D 3点组成一个圆,圆心为O1,连接O1与A、B、C、D 4点,若四边形ABCD进行零半径转向时的瞬时中心为O1,施加在A、B、C、D 4点上的作用力的垂直平面同样相交于同一直线上,4个力组成一个力偶系,合力为0,力偶作用中心为O1,不规则四边形作用力方向如图 5所示。
|
| 图 5 不规则四边形作用力方向 Fig.5 The direction of irregular quadrilateral force |
2.2 作用力的关系
在步进移运典型结构的零半径转向过程中,若F1、F2、F3和F4的合力不为0,结构会出现侧偏的现象,瞬时旋转中心会向着4力合力的方向进行移动。因此,在不考虑侧偏影响的情况下,只有保证F1、F2、F3和F4 4力的合力大小为0,才可以实现四边形在零半径转向时瞬时中心的稳定。如图 4所示,按照力的平移定理,只需要使力F1、F2、F3和F4均大于f0,其中f0为实际旋转过程中的摩擦力。
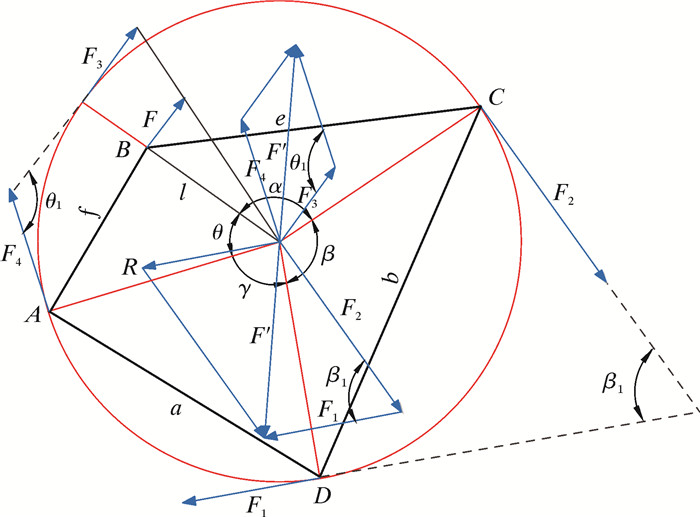
在图 5的情况下,对F1、F2、F3和F4相互间的关系进行推导。按照力的平移定理,可以把作用在刚体上的某点的力平移到任意一点,但必须同时附加一个力偶,这个附加力偶的矩等于原来的力对新作用点B的矩,平移后的各作用力如图 6所示。平移后的力偶即为带动刚体旋转的力偶。
|
| 图 6 力的平移 Fig.6 Force translation |
由图 6可知,若要使得四边形ABCD绕圆心进行旋转,必须保证力F1、F2、F3和F4的合力为0,即∑F=0,依据三角形余弦定理,则可得出下列关系式:
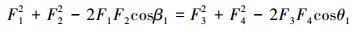
|
(1) |
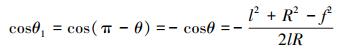
|
(2) |
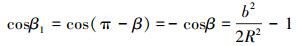
|
(3) |
式中:b、f表示四边形的2条边长,R表示三角形ADC外接圆半径,l表示圆心到四边形ABCD上顶点B的距离。
由公式(1)可知,任意2个力之间的关系,在假定另外2个力已知的情况下,2力关系满足二元二次方程,求解时需进行降次,按照图 7进行力的平移与求解,得出下列关系式:
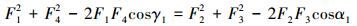
|
(4) |
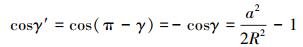
|
(5) |
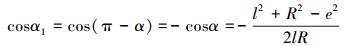
|
(6) |
式中:a、e表示四边形的2条边长。
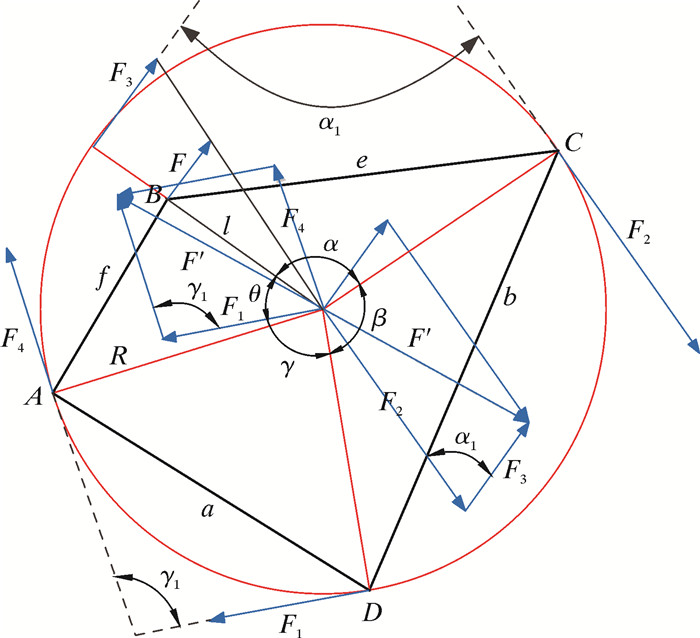
|
| 图 7 力的求解 Fig.7 Force solution |
Fig. 7由式(1)与式(4)可知,F3与F4之间的关系为:
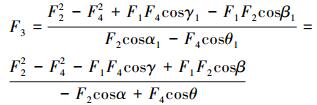
|
(7) |
同理,在已知F1、F2、F3、F4中任意2个力的情况下,可以求出另外2个力之间的关系。
综上所述,在不考虑摩擦力的情况下,步进位移装置进行零半径转向的必要条件为:施加在钻机模型4个角上的合力为0,各力大小大于步进装置处摩擦力,各力之间的关系如式(7)所示,且力矩不为0,力的方向沿着其自转轨迹圆的切向方向呈顺时针(或逆时针)分布。
3 运动仿真与结果验证UG NX是Unigraphics Solutions公司提供的集CAD/CAE/CAM为一体的大型软件,集建模、制图、加工、结构分析、运动分析和装配等功能于一体,广泛应用于机械制造领域[10]。运动仿真是UG数字仿真中的一个模块,可赋予模型各个部件一定的运动学特性,在各个部件之间设立一定的连接关系即可建立一个运动仿真模型,同时可进行图表输出等相关后续操作,从而验证运动机构设计的可实现性与合理性。
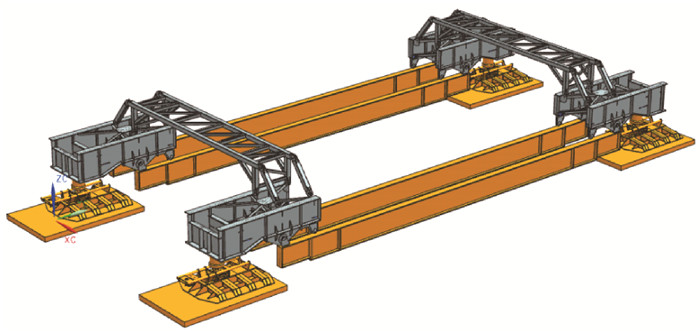
3.1 步进移运装置模型的建立UG具有丰富的建模功能,且其仿真模块与建模模块相互独立,因此可先建立主模型,然后依据不同的条件创建不同的仿真模块。按照哥伦比亚步进移运装置实际尺寸,通过拉伸、旋转和孔等特征命令,建立步进移运装置模型,如图 8所示。
|
| 图 8 步进移运装置模型 Fig.8 Model of walking device |
3.2 步进移运装置运动仿真及结果输出
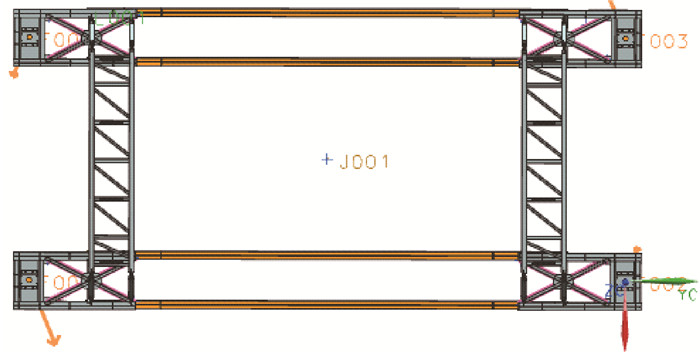
UG软件中运动仿真模块提供了标量力、矢量力、标量扭矩和矢量扭矩4种形式,其中标量力是有一定大小并通过空间直线方向作用的力,其方向只代表了初始的方向,在整个运动过程中方向不断变化,结合前文数学模型与理论计算,忽略摩擦力的影响,对步进移运装置施加特定大小的标量力,如图 9所示。图中箭头所指方向即为力的作用方向。
|
| 图 9 标量力的施加方向 Fig.9 The application direction of scalar force |
在仿真过程中只添加了模型的驱动力,而没有添加摩擦力,因此,步进移运装置在整个仿真过程中只受到驱动力的影响,在自转过程中会产生一个角加速度,在旋转过程中受到角速度的作用会越转越快。
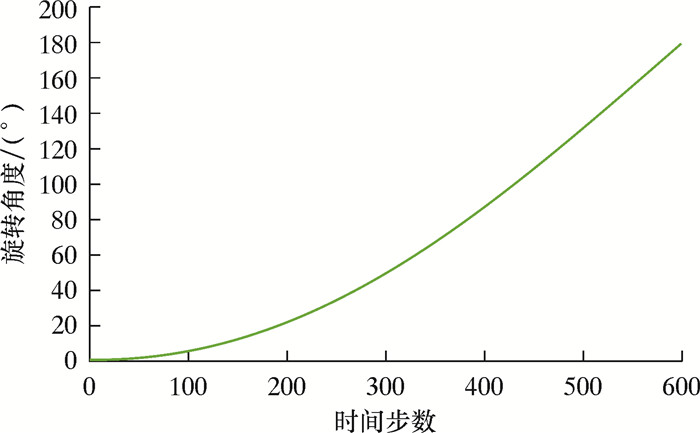
步进移运装置角度的变化曲线如图 10所示。由图可知,钻机旋转角度的变化随着时间步数递增,基本符合理论的预期变化。
|
| 图 10 步进移运装置角度变化曲线 Fig.10 Angle curve of walking device |
在角加速度的作用下,步进装置自转速度会越来越快,由向心力公式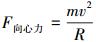
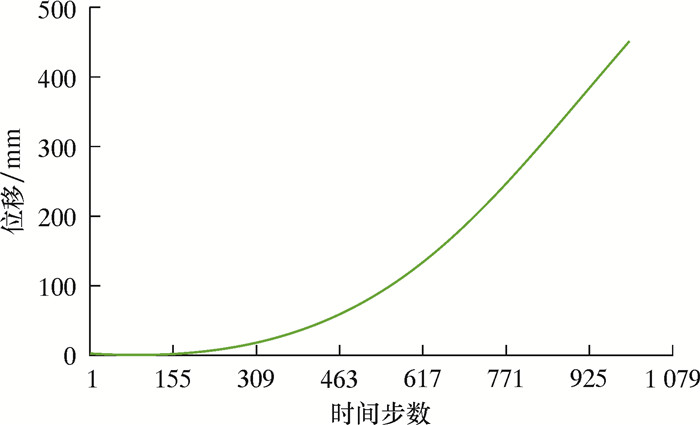
步进移运装置位移变化曲线如图 11所示。由图可知,步进装置的位移在0~200时间步数之内变化基本为零,在超过200时间步数之后,位移变化呈递增趋势。
|
| 图 11 步进移运装置位移变化曲线 Fig.11 Displacement curve of walking device |
3.3 不规则四边形结构自转运动仿真及结果验证
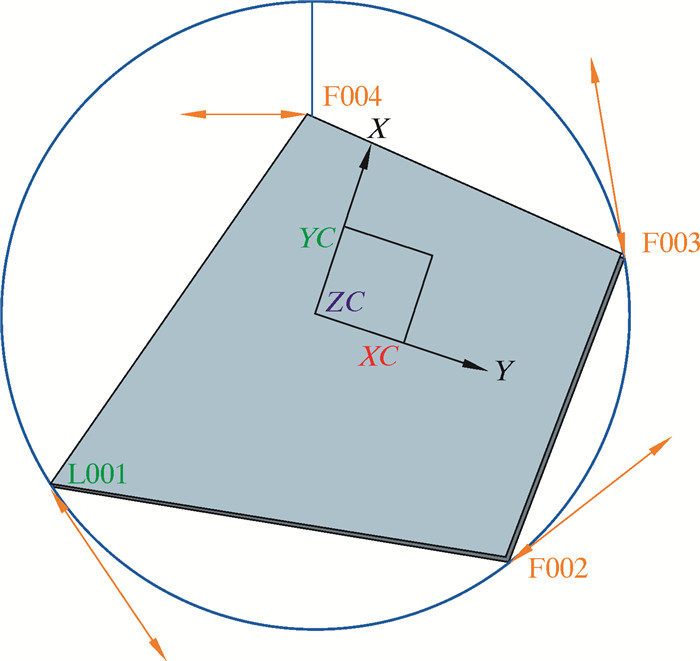
以地面为XY平面建立坐标系,建立不规则四边形简化的结构模型,如图 12所示。其中不规则四边形结构4个顶点上的4条线表示施加在不规则四边形结构上的力。
|
| 图 12 不规则四边形结构简化模型 Fig.12 Simplified model of irregular quadrilateral structure |
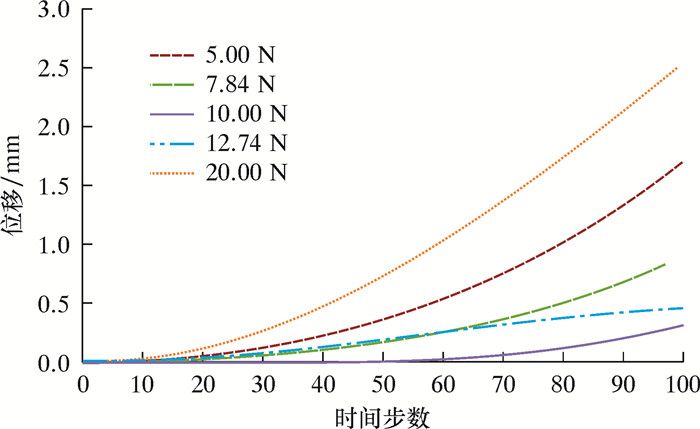
设定时间步数为100,按照前文所述的方法,首先对其外接圆上的3个力施加相同大小的力,设定初始值为F=10 N,对不在其外接圆上的力以10 N的大小进行随机波动,分析其在不同力的作用下不规则四边形中心的位移变化,分析结果如图 13所示。
|
| 图 13 位移变化图 Fig.13 Displacement diagram |
由图 13可知,在不同的力作用下,四边形的位移变化基本与前文叙述变化趋势相同,其中,当力F1=10 N时,四边形中心位移保持不变的时间最长,结合式(7)可知,不论四边形形状如何变化,若要其能够实现自转,施加在四角上的力大小应该相等。
对比当力F=10 N时,四边形中心的位移与角度变化如图 14所示。由图可知,在位移变化为0.005 mm时,角度幅值变化2.941°;当位移变化为0.010 mm时,其角度幅值变化7.727°;当位移为0.100 mm时,其角度幅值变化20.000°。
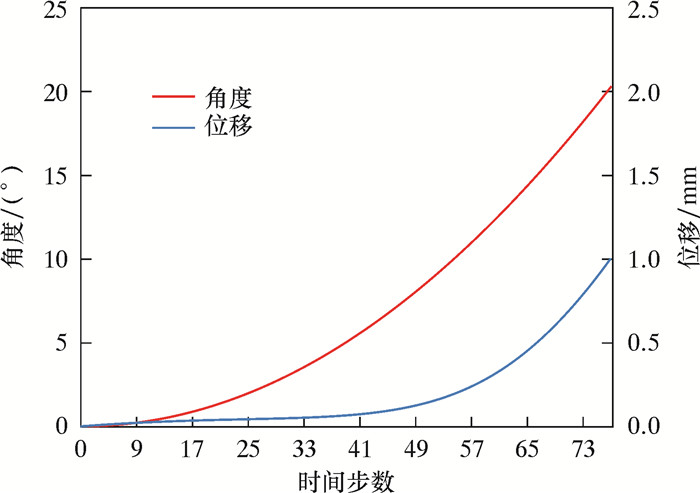
|
| 图 14 位移角度变化图 Fig.14 Displacement angle change diagram |
综上所述,在不考虑摩擦力的情况下,当施加在四边形四角上的力为固定值时,四边形在不发生位移情况下进行自转时,自转的角度有一个范围,即若要实现四边形的零半径转向,需要分步进行,每转过一定角度后需要对其进行调整才可以进行下一步的转动。可用此方法对步进移运装置进行运动学分析。
4 结论通过对滚动式步进移运装置结构及工作原理的分析,建立起三维模型进行力学分析及运动仿真,对其零半径转向的实现条件进行理论分析与结果验证,得到以下结论:
(1) 步进移运装置在零半径转向过程中可以视为一个四边形刚体的自转过程,4个顶点上力的施加方向应呈顺时针或者逆时针排列,各个力方向的垂直平面交于瞬时旋转中心,且以瞬时旋转中心为中心形成一个力偶系。
(2) 布局规则的钻机采用步进移运装置进行零半径转向的必要条件为:施加在钻机4角上油缸推力的合力为0,各力大小大于该位置的摩擦力,且力矩不为0,力的方向沿着其自转轨迹圆的切向方向呈顺时针(或逆时针)分布。
(3) 布局不规则钻机采用步进移运装置进行零半径转向的必要条件为:钻机4个顶点中至少有3个顶点的移动轨迹重合且形成一个圆形轨迹,旋转中心为该3个顶点组成三角形的外接圆圆心。4个角上的油缸推力为0,各个力的大小大于该位置的摩擦力,且力矩不为0。
(4) 步进装置在进行零半径转向时,需不断改变力的方向,以减少钻机中心的位移变化,若不对步进装置进行方向调整,则钻机无法准确到达指定井口。
| [1] | 孙守仁, 张长辉, 刘维国. 步进移运装置接地比压分析[J]. 石油机械, 2016, 44(9): 19–22. |
| [2] | 冯定, 唐海雄, 周魁, 等. 模块钻机的现状及发展趋势[J]. 石油机械, 2008, 36(9): 143–147. |
| [3] | 李磊. 快移快装钻机自行走系统[J]. 江汉石油科技, 2010, 20(4): 58–60. |
| [4] | 徐军, 高迅, 陈文征, 等. 钻机步进式移运装置的研制与应用[J]. 石油机械, 2015, 43(8): 37–40. |
| [5] | 王国治, 秦启章. 沙漠丛式井钻机滚动移位装置的研制[J]. 石油矿场机械, 1994, 23(4): 44–47. |
| [6] | 张清华, 秦世引, 万九卿. 轮式移动机器人零半径转向过程PID控制解析设计与实现[C]//中国人工智能进展2005. 北京: 北京邮电大学出版社, 1259-1264. |
| [7] | 王久飞. 汽车转向的力学分析[D]. 庆阳: 陇东学院, 2014. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hndx200102005&dbname=CJFD&dbcode=CJFQ |
| [8] | 叶敏. 四轮转向试验平台的建模仿真与实验研究[D]. 西安: 长安大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-11941-2004133170.htm |
| [9] | 范钦珊. 工程力学[M]. 北京: 机械工业出版社, 2002. |
| [10] | 吕洋波, 胡仁暮. UG NX7.0动力学与有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2010. |




