0 引言
山地长输管道分布范围广,沿途的自然环境和地质条件复杂,除自然跨越山谷的悬空管道外,埋地管道由于水流冲刷、地表塌陷和滑坡等地质灾害造成意外悬空也十分常见。悬空管道容易遭受地震破坏,进而造成重大经济损失和环境灾害。因此,研究悬空长输管道在地震载荷作用下的动力响应及破坏机制是当前学者们关注的重要问题。
N.M.NEWMARK[1]在20世纪60年代初首次对埋地管线进行了抗震研究,假定管道和土一起运动的同时忽略了惯性力的影响。
20世纪70年代,A.HINDY等[2]对NEWMARK的理论进行改进后首次提出管-土相互作用的概念,并对管道埋深和管径等因素进行了系统研究。邢静忠等[3]利用细长梁的小挠度理论对有轴向力作用下埋设于线弹性土壤中的悬跨管道进行了振动分析。刘志军等[4]充分考虑管-土相互作用和支座非线性等因素,建立了管线运动方程,并采用非线性增量有限元方法对悬垂管道在地震载荷作用下的动力响应进行了分析,但该运动方程不能反映管道各点的应力和应变。采用有限元数值模拟方法可较好地研究应力及应变沿管轴方向的变化情况。国内学者中,冉龙飞和赵林等[5-6]对悬空长输管道有限元建模方法进行了研究。孙健[7]借助有限元软件对悬空管道进行了模态和地震响应分析,赵潇等[8]采用ABAQUS有限元软件,在模态分析的基础上采用谱分析方法对悬空管道进行了动力响应分析,并分析了不同烈度下管线的位移和应力响应,但这些研究中很少对管径等多参数下的悬空管道动力响应进行分析。
笔者运用有限元软件ABAQUS,对不同悬空长度、不同管径、不同壁厚和不同土壤参数下悬空长输管道的动力响应进行研究,并对悬空管道在地震载荷作用下的受力特点进行了分析。
1 数值模型基本假设在ABAQUS软件中,可用主控-从属接触算法处理管土相互作用中的接触面问题[9-10],管土相互作过程中,埋设于土壤中的管道,其变形模量往往高于土壤的变形模量。管土相互作用的交界面上易产生剪切滑移等现象[11],因此用ABAQUS模拟管土相互作用时,为获得真实的模拟结构,可选用单纯的接触面算法。
地震载荷作用下,管道悬空时管土相互作用过程会受到诸多因素的影响。为了方便分析,通常会忽略影响较小的因素,因此在建立模型时,假设管道呈水平方向铺设且无落差、忽略温度变化、流固耦合作用且管体表面无缺陷。
2 本构模型及土体参数 2.1 管材的本构模型管线的材质选取X60管线钢,国内学者马廷霞等[12]对X60管线钢在单向拉伸状态下的全局二段式应力-应变关系式进行修正并提出了更为合理的本构关系模型,其表达式为:
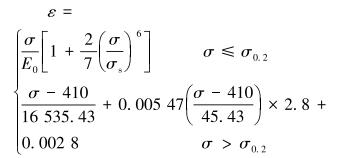
|
(1) |
式中:E0为材料初始弹性模量,MPa;σ为拉伸应力,MPa; ε为拉伸应变,无量纲; σs为材料屈服强度,MPa; σ0.2为极限屈服应力,MPa。
2.2 土体参数在ABAQUS中提供了多种土体模型,如Drucker-Prager模型、摩尔库伦模型和Cap-Drucker-Prager模型等。其中土体的摩尔库伦模型考虑到了屈服面的大小变化,可通过控制黏聚力的大小来实现。同时通过指定弹性模量、密度、泊松比、摩擦角、膨胀角以及黏聚力与相应的塑性应变,各项参数能够较好地反映土体的弹塑性力学。各种类型的土壤参数如表 1所示。
| 土的类型 | 弹性模量/ MPa |
泊松比 | 密度/ (kg·m3) |
摩察角/ (°) |
膨胀角/ (°) |
黏聚力/ kPa |
| 黏土 | 10.5 | 0.30 | 2 000 | 25 | 22 | 25 |
| 石灰岩 | 4 396.0 | 0.23 | 2 720 | 45 | 0 | 230 |
3 数值模型的建立
管线在铺设过程中,上覆土层厚度一般为1~2 m,笔者在此选择2 m作为埋深。管道的埋地端与土的相互作用区域半无限,因此在用有限元模拟时需将无限区域有限化。将土箱简化为一个宽和深度都为10 m的长方体,根据沉管作业过程中应力和应变远程监测数据表明,管道沉降作业区两侧埋地端受影响区仅为悬空长度的0.4倍,设定土体长度为悬空长度的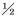
悬空管道的动力响应研究属于弹塑性大应变分析问题,网格在分析过程中存在扭转变形,土体可选择8节点线性减缩单元(C3D8R),而管道由于其几何特性,为保证管道单元在计算过程中网格不过度变形,管道单元可采用三维4节点减缩壳单元(S4R),在厚度方向可设置5个积分节点。划分网格后的模型见图 1。

|
| 图 1 悬空管道划分网格后模型图 Fig.1 The model of the pipeline after meshing |
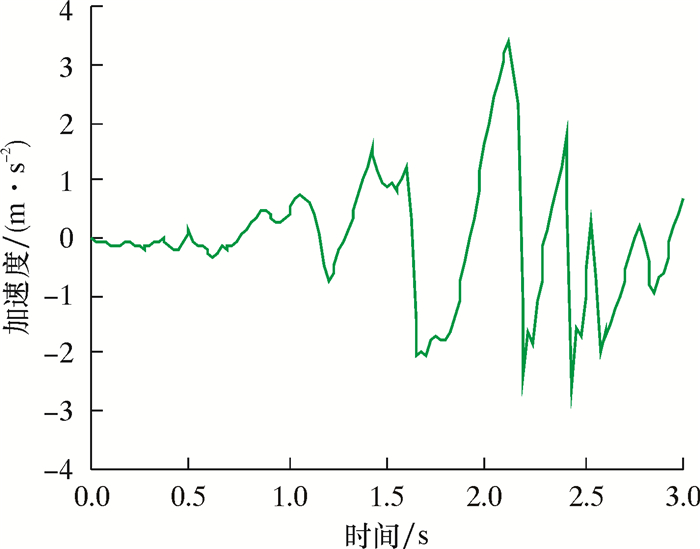
地震波的频率多在1~10 Hz范围内,与埋地管道固有频率相近,容易发生共振现象。为有效地模拟管道在地震载荷作用下的动力响应,根据地震发生时所在场地记录到的地面运动加速度数据, 将随时间变化的加速度载荷施加在模型边界上。选取的地震波加速度时程曲线如图 2所示。埋地管道悬空段与土体的交界处(内出土端),受悬空管道动力载荷的影响发生竖向位移一般比水平位移大,因此可将内出土端设置成只出现竖向位移,约束住其他方向的位移。埋地段的最上层土面为自由面[13]。
|
| 图 2 地震波加速度时程曲线 Fig.2 Time-history curve of seismic wave acceleration |
4 数值模拟结果与分析 4.1 悬空长度对管道动力响应的影响分析
为了解悬空长度对管道动力响应的影响,在其他参数保持不变的情况下,悬空段长度分别取35、40、45、50、60、70、80和100 m,土体参数选择黏性土,管道壁厚7.4 mm,管径为508.0 mm。经模拟,不同悬空长度的埋地管道在相同地震作用下的最大应力及位移云图分别如图 3和图 4所示。不同悬空长度下管道的峰值应力及峰值位移数据见表 2。悬空长度为40 m时管道峰值应力为471.0 MPa,位移为0.773 m,其地震反应显著大于悬空长度为35及45 m的管道,说明在此悬空长度下管道的自振频率与地震波的频率相近,发生了共振现象。当悬空长度分别为45、60、70、80、90和100 m时,峰值应力逐步增大,对比不同悬空长度下管道的峰值位移的变化情况,其变化规律同峰值应力相似。因此,管道的悬空长度是影响地震反应的一个重要因素。

|
| 图 3 悬空长度40 m时管道上峰值应力云图 Fig.3 Peak stress distribution on pipeline with suspension length of 40 m |
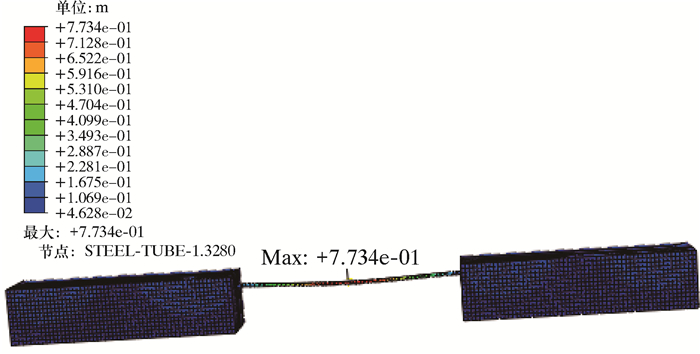
|
| 图 4 悬空长度40 m时管道位移云图 Fig.4 Displacement distribution on pipeline with suspension length of 40 m |
| 悬空长度/m | 峰值应力/MPa | 峰值位移/m |
| 35 | 368.6 | 0.592 |
| 40 | 471.0 | 0.773 |
| 45 | 378.0 | 0.609 |
| 50 | 391.1 | 0.766 |
| 60 | 406.4 | 1.214 |
| 70 | 465.2 | 1.717 |
| 80 | 509.5 | 2.241 |
| 100 | 535.0 | 2.985 |
4.2 管径对管道动力响应的影响分析
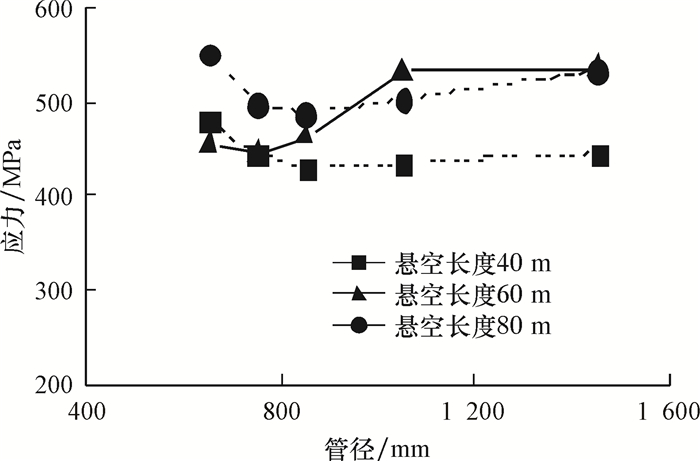
利用壁厚为13.4 mm,土壤为黏性时,管径分别为650、750、850、1 050和1 450 mm的管道进行模拟分析。不同管径时各管道在地震载荷作用下的应力峰值和位移值变化情况分别如图 5和图 6所示。由图 5可知,在悬空长度为40、60和80 m时,随着管径的增大,管道的峰值应力呈现出先减小后增大的规律。这是由于管径在较小范围内,随着管径增大,管道刚度逐渐增大所造成的影响小于管径增大所造成的地震载荷效应放大产生的影响,当管径增大至较大值时,刚度增大所造成的影响开始大于管径增大所造成的载荷效应放大产生的影响。由图 6可知,管道的峰值位移随着管径的增大逐渐减小。根据模拟得到的数据表明管径对于地震载荷作用下管道的动力响应具有较大的影响。
|
| 图 5 管径对峰值应力的影响 Fig.5 Effect of pipe diameter on peak stress |

|
| 图 6 管径对峰值位移的影响 Fig.6 Effect of pipe diameter on peak displacement |
4.3 壁厚对管道动力响应的影响分析
为研究不同壁厚对于管道地震反应的影响,模拟管径为508 mm、悬空长度为80 m时不同壁厚管道的动力响应。表 3为不同壁厚时的峰值应力及峰值位移。对比发现,随着壁厚的增大,应力增大幅值分别为0.1%、0.7%和1.0%;峰值位移由2.243 m增至2.691 m,增大幅值分别为7.6%、6.2%和5.1%。这表明壁厚对管道峰值应力影响较小,可忽略不计,但对峰值位移有一定的影响。
| 壁厚/mm | 峰值应力/MPa | 峰值位移/m |
| 7.4 | 509.5 | 2.241 |
| 10.4 | 510.3 | 2.413 |
| 13.4 | 514.3 | 2.561 |
| 16.4 | 518.4 | 2.691 |
4.4 土壤类型对悬空管道动力响应的影响分析
埋地管道在长距离运输过程中往往会穿越不同类型的土层,在不同的土层中管道的地震响应必然会有差异,土的弹性模量可以衡量弹性变形能力,是不同类型土弹性特性的突出表现。笔者选取2种性质差异较大的土壤进行有限元分析。其具体参数见表 1。通过对比在悬空长度分别为40、80和100 m时2种土壤对管道应力和位移情况的影响。分析后得到的应力和位移结果如表 4所示。分析表明,在相同地震载荷作用下,随着着悬空长度的变化,埋设于石灰岩中的悬空管道其峰值应力及峰值位移皆小于埋设于黏性土中的悬空管道,说明不同的土壤类型对管道产生的动力响应影响差异较大,管道不宜铺设在弹性模量较小的黏土中。
| 悬空长度/m | 黏性土 | 石灰岩 | |||
| 峰值应力/MPa | 峰值位移/m | 峰值应力/MPa | 峰值位移/m | ||
| 40 | 471.9 | 0.733 | 179.3 | 0.205 | |
| 80 | 509.5 | 2.241 | 479.6 | 1.201 | |
| 100 | 535.0 | 2.980 | 535.1 | 1.743 | |
4.5 地震载荷作用下悬空管道的受力特点
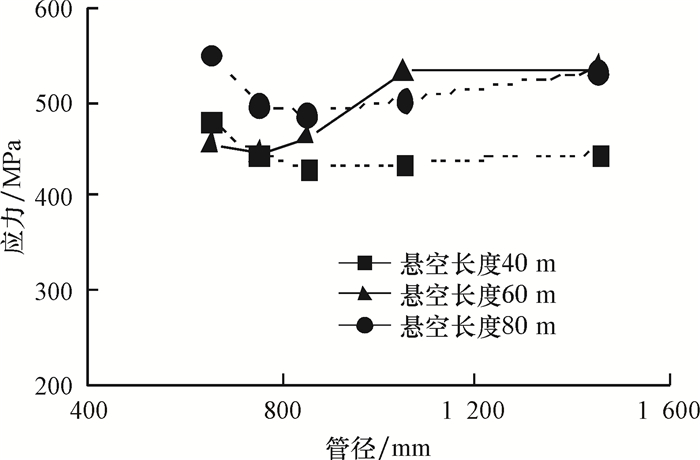
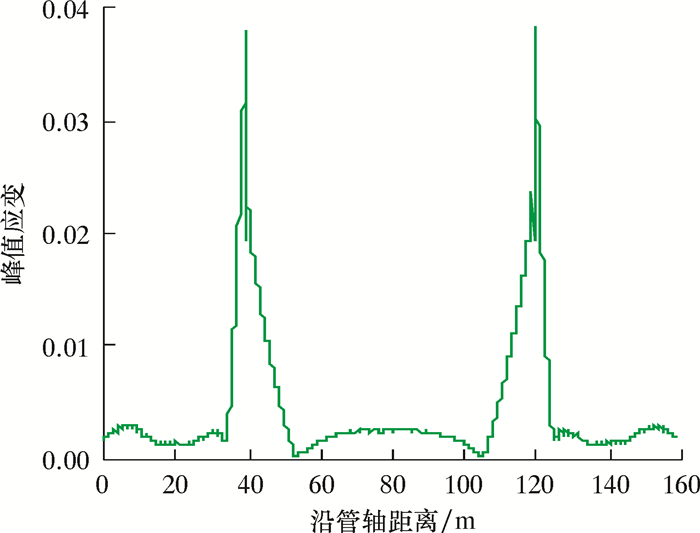
悬空管道在地震载荷作用下,管道上各部分的应力及应变会出现差异。为了解管道上应力及应变的分布情况,选择悬空长度80 m、管径508 mm、壁厚16.4 mm的管道进行分析研究。沿着管道应力峰值点(管道顶部)定义一条管轴方向的路径,管道上应力及应变沿着路径的分布情况如图 7和图 8所示。管道Mises应力分布云图如图 9所示。从图中可以看出,路径上应力、应变变化趋势大体一致。悬空管道与土体接触段应力变化不大,且维持在较小水平,达到35 m左右时管道应力突然增大且于40 m(内出土端)处达到峰值,随后逐渐减小且于53 m处达到最小,随后应力又逐渐增大并于跨中时达到局部最大值。由分析可知,管道由于受到重力及地震载荷作用,在内出土端管道受弯矩的影响应力值较大,而管道与土壤相互接触的埋地段受弯矩影响较小,地震载荷对管道的应力起主要作用。
|
| 图 7 沿管轴应力变化曲线 Fig.7 Stress curve along the pipeline axis |
|
| 图 8 沿管轴应变变化曲线 Fig.8 Strain curve along the pipeline axis |

|
| 图 9 管道应力分布云图 Fig.9 Pipeline stress distribution |
5 结论
(1) 在地震载荷作用下,随着悬空长度的增加,管道的峰值应力及峰值位移都会显著增大,尤其是当管道的自振频率与地震波的频率相近时发生共振,管道的动力响应会显著增大。
(2) 在一定的管径范围内,随着管径的增大,峰值应力及峰值位移会逐渐减小, 当到达临界值后,峰值应力会随管径增大而增大。
(3) 壁厚对管道峰值应力影响较小,可忽略不计,但对峰值位移有一定的影响。
(4) 不同的土壤类型由于其力学性质的不同,使得管道在地震载荷作用下的动力响应存在较大差异,且管道不宜铺设在弹性模量较小的黏土中。
(5) 悬空管道在地震载荷作用下,其峰值应力总出现在管道的内出土端附近且应力和应变沿管轴方向呈现出一定的分布规律。
| [1] | NEWMARK N M.Problems in wave propagation in soil and rock[C]//Proc. of international symposium on wave propagation and dynamic properties of earth materials. Albuquerque N M: University of New Mexico Press, 1968:7-26. |
| [2] | HINDY A, NOVAK M. Earthquake responseof underground pipelines[J]. Earthquake Engineering and Structural Dynamics, 1979, 7(5): 451–476. DOI: 10.1002/(ISSN)1096-9845 |
| [3] | 邢静忠, 柳春图. 线弹性土壤中埋设悬跨管道的弯曲和振动特性[J]. 海洋工程, 2008, 26(2): 78–82. |
| [4] | 刘志军, 倪立峰, 周星德, 等. 悬垂管道跨越结构地震反应分析[J]. 地震工程与工程振动, 2004, 24(5): 123–126. |
| [5] | 冉龙飞, 王晓霖. 埋地悬空管道的安全评估影响因素研究[J]. 化工设备与管道, 2016, 53(6): 81–86. |
| [6] | 赵林, 冯启民. 埋地管线有限元建模方法研究[J]. 地震工程与工程振动, 2001, 21(2): 53–57. |
| [7] | 孙健. 基于ABAQUS的悬空管道地震响应分析[J]. 石油和化工设备, 2014, 17(7): 30–33. |
| [8] | 赵潇, 马廷霞, 谢娜娜. 地震波动下悬空管道的动力响应分析[J]. 石油机械, 2014, 42(3): 110–114. |
| [9] | 朱向荣, 王金昌. ABAQUS软件中部分土模型简介及其工程应用[J]. 岩土力学, 2004, 25(增刊1): 144–148. |
| [10] | 杨海建, 张伟. 基于接触单元的海底管道地震动力时程分析[J]. 港工技术, 2016, 53(增刊1): 6–9. |
| [11] | 任艳荣, 刘玉标, 顾小芸. 用ABAQUS软件处理管土相互作用中的接触面问题[J]. 力学与实践, 2004, 26(6): 43–45. |
| [12] | 马廷霞, 杨永和, 许震, 等. X60管线钢的本构关系及失效判据[J]. 重庆大学学报, 2014, 37(8): 67–75. DOI: 10.11835/j.issn.1000-582X.2014.08.010 |
| [13] | 武立伟. 埋地管道极限悬空长度研究[D]. 西安: 西安石油大学, 2015: 27-28. http://cdmd.cnki.com.cn/Article/CDMD-10705-1015307434.htm |




