0 引言
目前,我国浅层油田和煤矿的开采已经进入尾声,然而,对于能源的需求却日趋增长。深井作业力度不断加大。由于钻井深度增加需要跨越各种各样的地质构造,使得新煤矿和油矿的建立难度加大[1]。特别是在高深度、高压力和高应力条件下,地质构造更是复杂,处理难度也更大。工业CT可以对石油开采过程中的动力平台、石油勘探岩心以及井下工具等进行无损检测与无损测量,为开采过程中安全与效益的分析提供可靠的保障[2]。
国内外对于工业CT的研制已经取得了一定的成果,美国、英国和日本等国家工业CT朝着超大、超小型物体高精度检测方向发展[3]。工业CT对控制器控制精度的要求不断提升,为此,需要寻求高效的控制系统与控制策略。在国内,范声锋[4]建立了基于模糊PID交叉耦合控制的射线源-探测器双轴位置伺服控制系统模型,对于工业CT双轴位置伺服同步运动控制技术进行了研究。G.YUAN等[5]采用主从同步控制方式实现螺旋扫描模式下2电机的同步化,同时采用级联控制方式提高每台电机的稳定性。L.OU等[6]通过V++设计控制软件,提出基于高能量工业CT的FPGA的嵌入式同步系统,并用试验加以验证。A.DAUM[7]通过无线方式在控制系统中接入控制元件,提高了控制精度。
上述控制系统设计过程较为复杂。然而,对于工业CT试验台加载系统位置控制来说,只需保证其误差在一定范围内即可。笔者提出了一种基于电液位置控制的模糊PID,用于工业CT试验台加载系统的位置控制。仿真与试验结果表明:所设计的模糊PID控制器跟踪性能良好,可以满足工程实际应用。
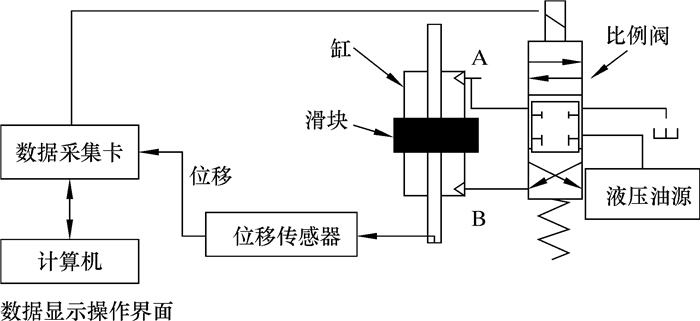
1 试验系统设计设计中,液压缸最大输出力10 kN,最大输出位移45 cm,加载工作压力19~20 MPa,加载速度v0=10 mm/s,回程速度(空载)v1=20 mm/s,位移分辨率0.01 mm,系统控制精度±5%。试验的硬件设备包括24 V电源、压力传感器、比例阀、缸、位移传感器和数据采集卡等,试验原理如图 1所示。
|
| 图 1 试验原理图 Fig.1 Schematic diagram of the test |
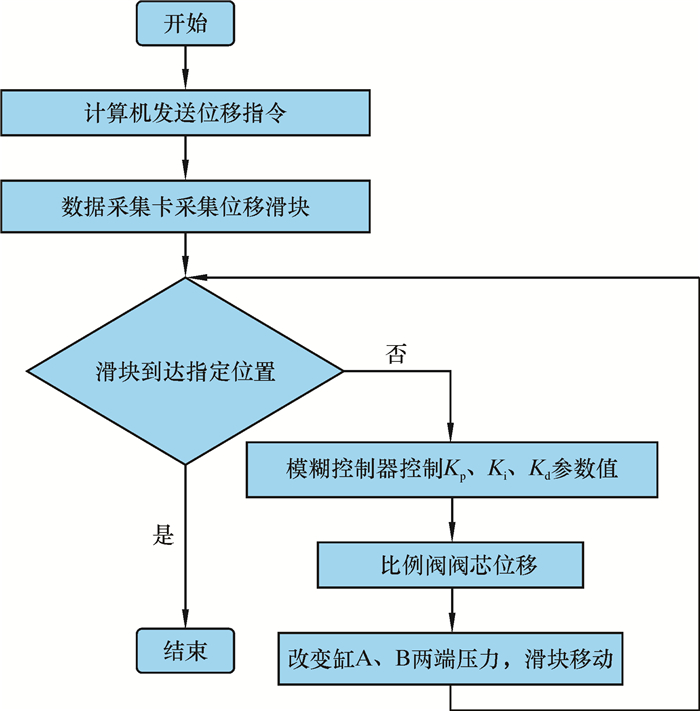
计算机发送位移指令,通过控制阀芯位移来改变缸两端压力;同时,计算机接受数据采集卡的信号,并不断调整模糊PID控制器的输出,从而使活塞杆达到指定位置。具体的试验流程如图 2所示。图中Kp、Ki、Kd分别表示比例系数、积分系数和微分系数。
|
| 图 2 试验流程图 Fig.2 Test flow chart |
2 模型建立及控制器设计 2.1 数学建模
在建模过程中,做以下假设:
(1) 假设所选用的伺服阀是理想的零开口四通阀;
(2) 假设系统压力源为恒压油源,无回油,即回油压力为0,同时不考虑系统的内泄;
(3) 假设回路管道是理想的短粗管道,可以忽略管内的各种质量及动态情况;
(4) 假设液压缸的各个工作腔及压力都相等,并且液压油的体积弹性模量和油温均为定值,不随外界工作环境的改变而发生变化[8-9]。
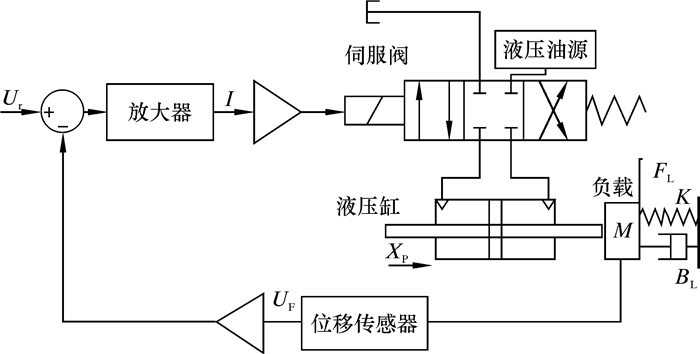
电液位移控制系统的原理图如图 3所示。
|
| 图 3 电液位移控制系统原理图 Fig.3 Schematic diagram of electro-hydraulic displacement control system |
由此建立液压动力元件的流量方程、连续性方程以及平衡方程,并进行拉普拉斯变换:
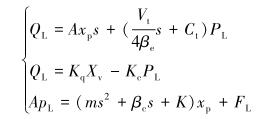
|
(1) |
式中:A为活塞有效面积,xp为活塞杆位移,Vt为液压缸总体积,K为负载的弹簧刚度,βe为液体的体积弹性模数,FL为液压缸负载力,βc为阻尼系数,m为负载等效质量,Kc为阀压力流量系数,Kq为阀流量增益,Ct为缸的泄漏系数,PL为负载压降,Xv为伺服阀阀芯位移。
电液伺服阀的传递函数可近似为:
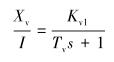
|
(2) |
式中:I为放大器输出电流,Kv1为伺服阀增益,Tv为伺服阀时间常数。
不考虑外在干扰时,位移控制系统方框图见图 4。由此可以得出系统的开环函数为:
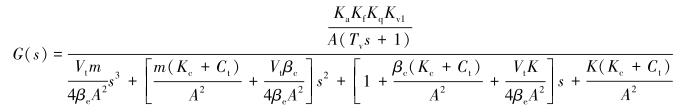
|
(3) |

|
| 图 4 位移控制系统方框图 Fig.4 Block diagram of displacement control system |
式中:Ka为放大器增益,Kf为位移传感器系数。
通过一系列静态和动态计算,确定活塞有效面积、系统开环增益、伺服阀参数和负载的刚度等参数。其中,恒压油源压力ps=20 MPa,节流口流量系数Cd=0.65,液体弹性模量βe=700 MPa,节流口面积梯度W=0.023 m,油液密度ρ=850 kg/m3,阻尼系数βc=0.8 N·m/s。带入式(3),最终化简得系统的开环传递函数为:
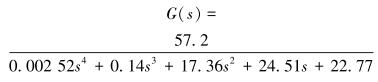
|
(4) |
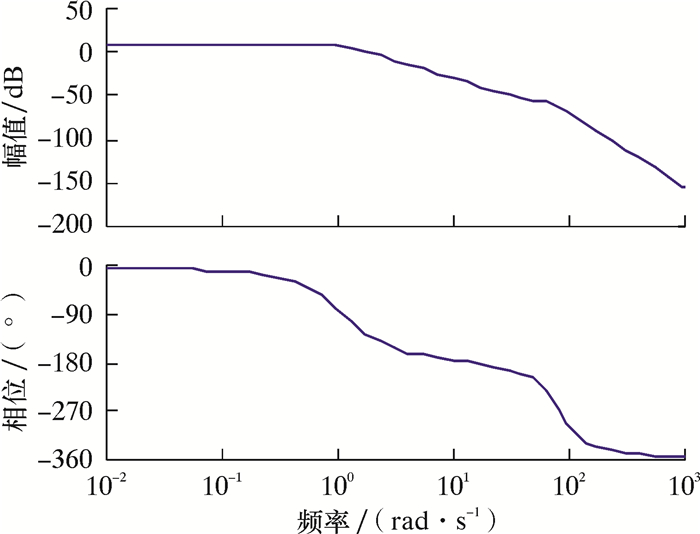
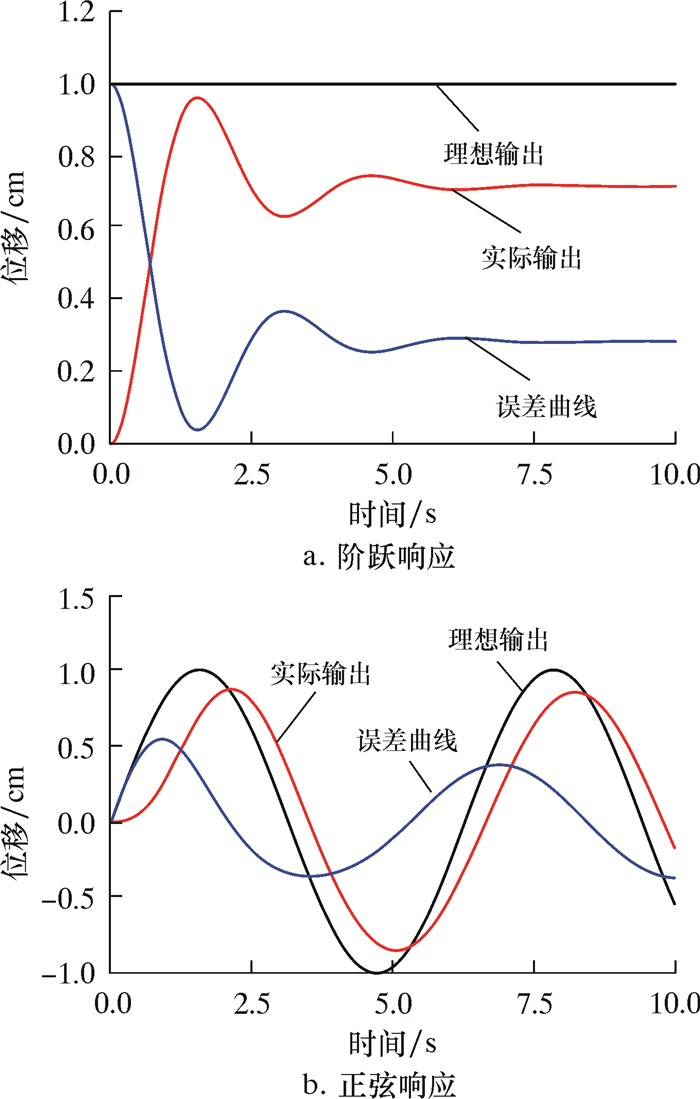
系统的开环Bode图如图 5所示。幅值裕度Gm=32 dB,相位裕度Pm=55°,电液位置控制系统稳定。闭环系统响应结果如图 6所示。从图中可以看出,系统到达稳定的过程中存在波动,且响应时间较长,为了进一步消除稳态误差,需要对这种系统进行有效的校正。
|
| 图 5 系统开环频域特性图 Fig.5 Open-loop frequency domain characteristics of the system |
|
| 图 6 闭环系统响应结果 Fig.6 Response results of the closed-loop system |
2.3 模糊PID控制器设计
模糊控制器采用2输入3输出结构,输入为误差E和误差变化率EC,输出为PID控制器的3个参数。对于不同的误差E和误差变化率EC,通过模糊推理,以达到调节PID参数的目的[10]。
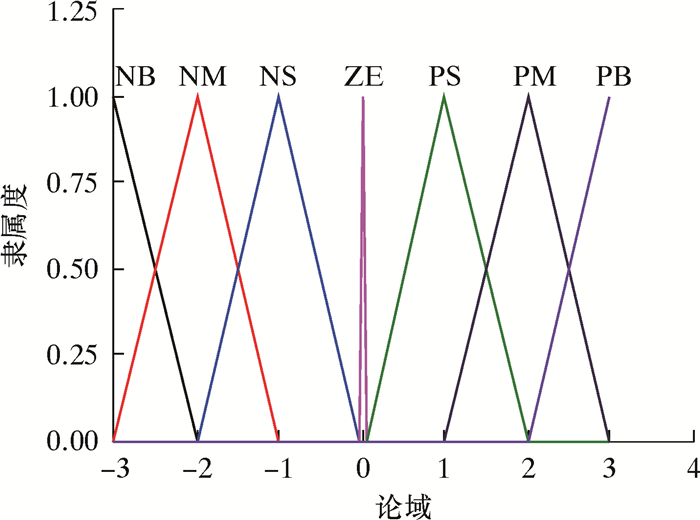
2.3.1 隶属函数的确立[11-12]E和EC可以分为7个模糊状态,即模糊集为:{NB,NM,NS,ZE,PS,PM,PB},子集中的元素分别代表负大,负中,负小,零,正小,正中,正大。模糊论域取为[-3 3],选择三角形隶属函数。隶属函数如图 7所示。
|
| 图 7 模糊PID控制器隶属函数 Fig.7 Membership function of fuzzy PID controller |
2.3.2 模糊规则表的制定
| 误差变化率 | 误差 | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | ZE | PB | PB | PS | PM | PS | ZE |
| NM | ZE | PM | PB | PM | PS | PS | ZE |
| NS | ZE | PS | PM | PS | ZE | ZE | ZE |
| ZE | ZE | ZE | PS | ZE | NS | ZE | ZE |
| PS | ZE | ZE | ZE | NM | NM | ZE | ZE |
| PM | ZE | NS | NS | NM | NM | NM | ZE |
| PB | ZE | NS | NM | NB | NB | NB | ZE |
| 误差变化率 | 误差 | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | PB | PM | PS | PS | ZE | PM | PB |
| NM | PS | PM | PS | PS | ZE | PS | PS |
| NS | NS | NM | NS | ZE | ZE | PS | PS |
| ZE | NM | NM | NS | ZE | NM | PS | PM |
| PS | NM | NM | ZE | ZE | PS | PM | PM |
| PM | NS | NS | PS | PS | PS | PM | PS |
| PB | NS | ZE | PS | PS | PM | PB | PS |
| 误差变化率 | 误差 | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | PB | PM | PS | PS | ZE | PM | PB |
| NM | PS | PM | PS | PS | ZE | PS | PS |
| NS | NS | NM | NS | ZE | ZE | PS | PS |
| ZE | NM | NM | NS | ZE | NM | PS | PM |
| PS | NM | NM | ZE | ZE | PS | PM | PM |
| PM | NS | NS | PS | PS | PS | PM | PS |
| PB | NS | ZE | PS | PS | PM | PB | PS |
2.3.3 去模糊化
建立试验系统仿真的动态结构,如图 8所示。

|
| 图 8 模糊PID控制器仿真框图 Fig.8 Simulation diagram of the fuzzy PID controller |
2.3.4 响应结果
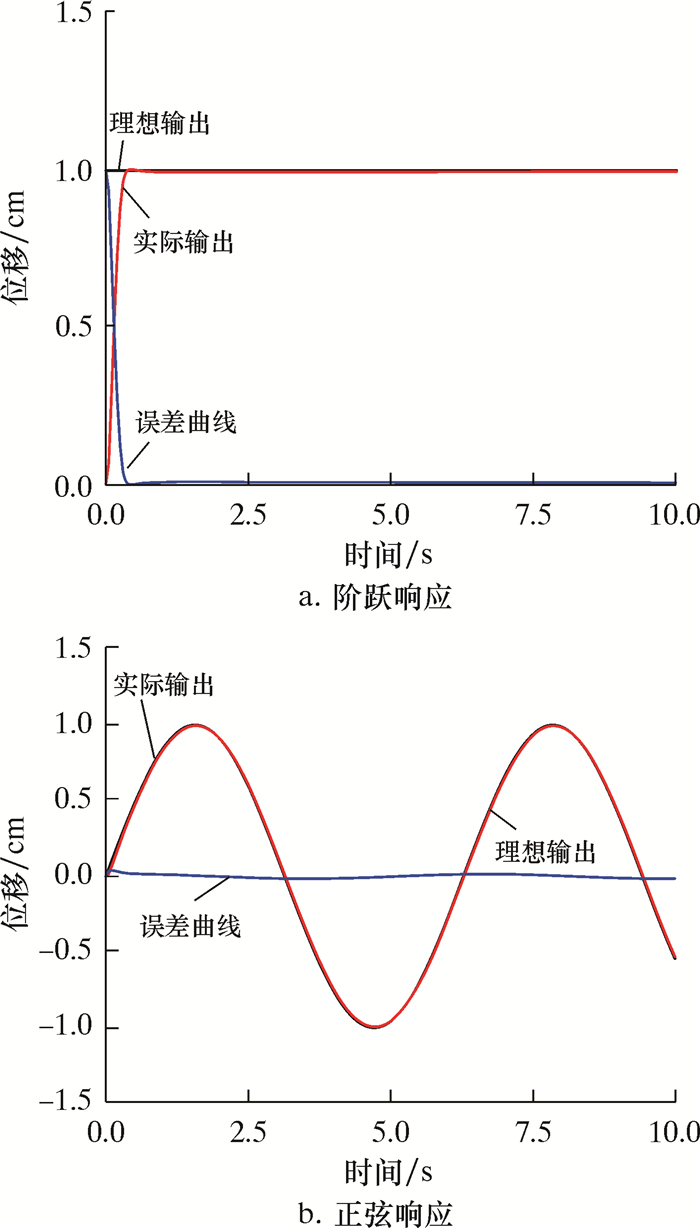
通过不断调整试验参数,选取仿真结果最好的一组参数, 取Ke=0.25,Kec=-0.025,Kp=3.5,Kp0=8.2,Ki0=1.1,Kd0=4.88。其阶跃响应仿真结果和误差曲线如图 9所示。使用模糊PID控制器阶跃响应时间为0.3 s左右,误差可控制在0.15%~0.50%,效果较为理想。
|
| 图 9 模糊PID系统响应结果 Fig.9 Response of the fuzzy PID system |
3 仿真及试验结果对比分析 3.1 仿真结果对比分析
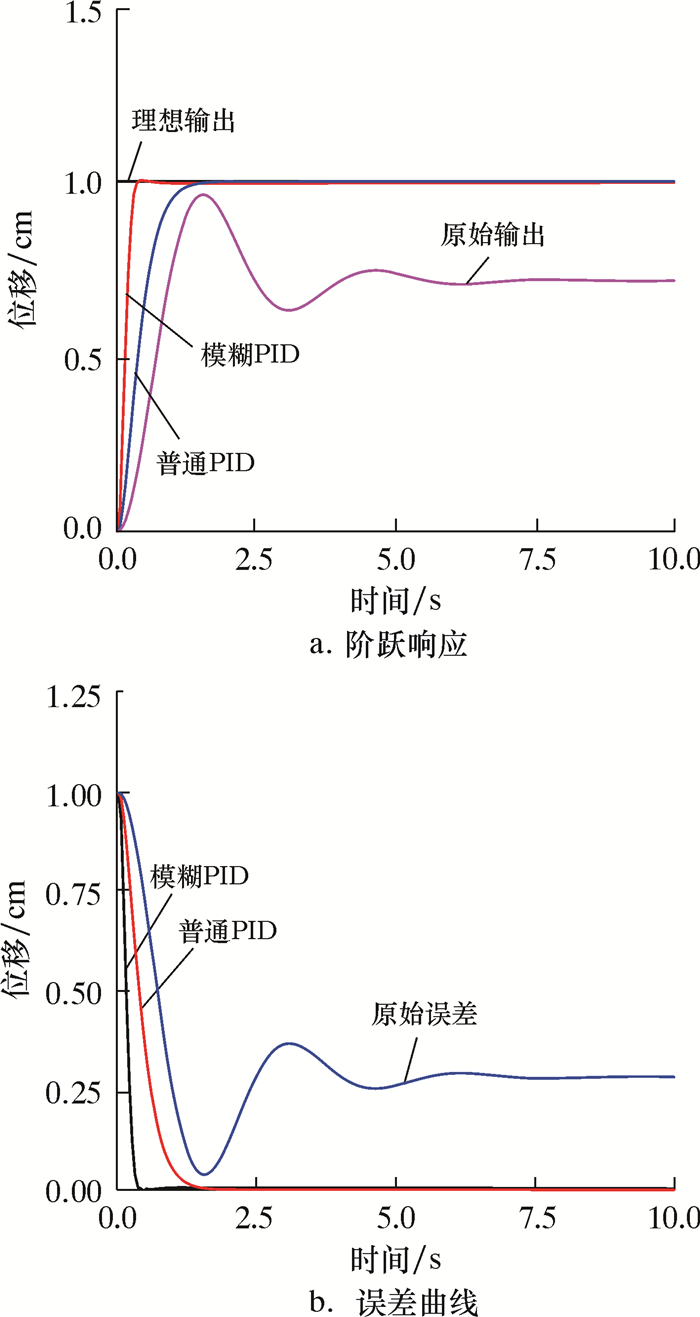
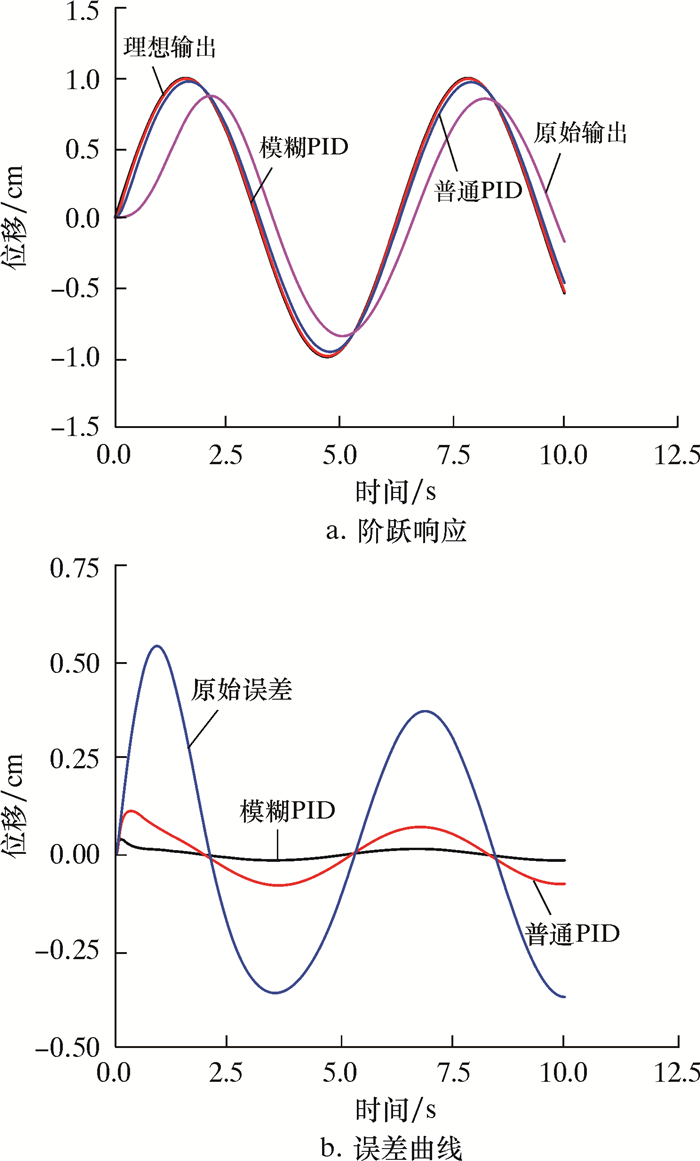
使用不同控制器时,系统响应曲线和误差曲线如图 10与图 11所示。通过比较可以发现,普通PID的响应时间可以达到1.8 s,而模糊PID控制器可以达到0.3 s左右。虽然传统PID控制器控制下的响应曲线已经可以满足系统的控制要求,但是模糊PID控制器控制的响应曲线拥有更好的响应速度。
|
| 图 10 不同控制器系统阶跃响应结果 Fig.10 Step response of different controller systems |
|
| 图 11 不同控制器系统正弦响应结果 Fig.11 Sine response of different controller systems |
3.2 试验结果对比分析
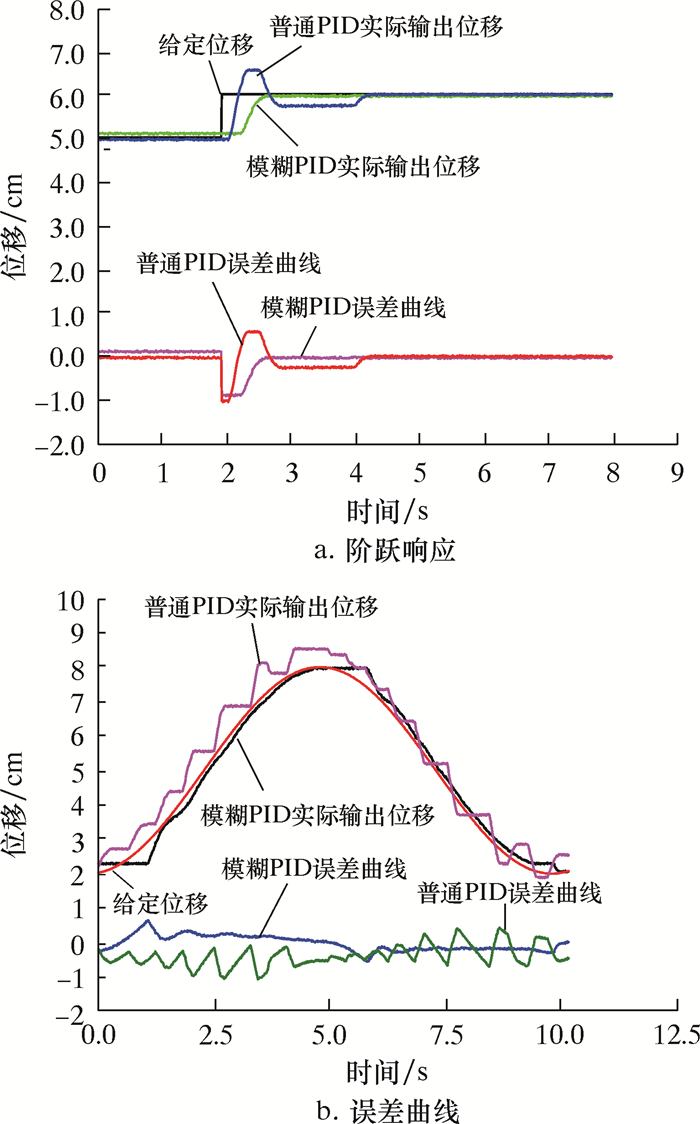
图 12为传统PID与模糊控制器阶跃响应的试验结果。通过对比试验结果可以看出,在阶跃的瞬间,无论采用哪种控制形式,滑块的移动均存在滞后现象。由于系统自身不稳定的影响,在响应过程中,会有震荡产生,且即使在达到平稳状态后,仍然会有微小的抖动;由于模糊PID控制器需要一定的计算时间,导致在前控制版面的显示窗口上出现了曲线不连续现象。对比普通PID和模糊PID的误差曲线可以看出,模糊PID的相对误差稳定在1%~6%之间。虽然存在抖动现象,但是所设计的模糊PID控制器的跟踪性能更好。
|
| 图 12 试验结果 Fig.12 Test results |
4 结论
(1) 仿真过程中,普通PID的响应时间可以达到1.8 s,最大误差为12%。而模糊PID控制器可以达到0.3 s左右,且响应的稳态误差可以控制在0.15%~0.50%之间。
(2) 试验结果表明:模糊PID的相对误差稳定在1%~6%之间,由此证明所设计的模糊PID的跟踪性能良好,可以满足工程实际应用。
| [1] | 刘子嘉. 结构加载试验系统液压驱动系统设计及控制方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014082234.htm |
| [2] | 武春利, 杨蓉, 陈学军, 等. 高精度工业CT技术在石油工业中的应用[C]//全国无损检测学术年会论文集. 上海: 中国机械工程学会无损检测分会, 2013: 908-912. |
| [3] | 王增勇, 汤光平, 李建文, 等. 工业CT技术进展及应用[J]. 无损检测, 2010(7): 504–508. |
| [4] | 范声锋. 工业CT双轴位置伺服同步运动控制技术研究[D]. 重庆: 重庆大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10611-1013044459.htm |
| [5] | YUAN G, ZHANG Y, XU P, et al. Analyse and researchon motion control for helical CT scanner[J]. Applied Mechanics & Materials, 2014, 687/688/689/690/691: 37–43. |
| [6] | OU L, HU D, CHEN H, et al. Design of embedded synchronization system for high energy industry CT based on fpGA[J]. High Power Laser and Particle Beams, 2011, 23(9): 2499–2502. DOI: 10.3788/HPLPB |
| [7] | DAUM A. CT system and method for determining the position and range of a mobile control element for control of the CT system:US20160296197[P]. 2016. |
| [8] | XIE W, WANG S K, WANG J Z, et al. Control method on serial type pump-valve coordinated electro-hydraulic servo system[J]. Journal of Beijing Institute of Technology, 2016(1): 100–107. |
| [9] | 李洪人. 液压控制系统[M]. 北京: 国防工业出版社, 1990. |
| [10] | 罗文君. 基于参数整定的模糊PID控制在水箱控制系统中的应用[D]. 长沙: 中南大学, 2011. |
| [11] | 曹旭妍. 基于模糊PID控制的电液力伺服系统的应用研究[J]. 工业控制计算机, 2014(9): 69–70. |
| [12] | 曹旭妍. 电液力伺服控制系统的应用研究[D]. 西安: 西安建筑科技大学, 2013. http://d.wanfangdata.com.cn/Periodical/csjsllyj2011361378 |
| [13] | 张德昌. 模糊自适应控制在电液力控伺服系统的应用研究[D]. 太原: 太原科技大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10109-1013183510.htm |



