2. 黑龙江省石油石化多相介质处理及污染防治重点实验室
2. Heilongjiang Provincial Key Laboratory of Petroleum and Petrochemical Multiphase Treatment and Pollution Prevention
0 引言
液-液分离水力旋流器是一种高效的离心分离设备,混合介质沿切向入口进入旋流腔,由于离心力作用重质相从底流口排出,轻质相从溢流口排出[1]。水力旋流器在完成旋流分离时,必须有一定的压力损耗,即水力旋流器根据压力的消耗换取分离所需的能量[2]。在旋流分离时,入口是预分离介质进入旋流器的首要通道,且入口处的压力损失可占总压力损失的40%左右[3-5]。因此,入口结构对水力旋流器的分离性能至关重要。艾志久等[6]利用数值模拟方法,对多种入口结构形式的油水旋流分离器进行了分离性能和流场计算,得出采用阿基米德螺旋线入口形式的旋流器能够得到较稳定的流场和较高的分离效率。蒋明虎等[7]介绍了一种轴流式分离器,入口结构采用螺旋叶片形式,并且对其进行模拟,分析了螺旋叶片的结构参数对分离器内部速度场和压力场的影响,并通过试验分析了不同操作参数对其分离效率的影响,证明导向式入口类型具有很高的分离效率和较低的压力损失。赵立新等[8]应用Fluent软件,计算了螺旋叶片入口形式对脱水型旋流器分离性能和压力特性的影响,研究结果表明:以轴向入口代替切向入口使得新型水力旋流器具有较好的分离效果。此外,由于轴向入口旋流器是轴向对称结构,相对于切向入口结构其能有效降低入口处循环流造成的影响,提高分离效率;同时,入口位置湍流作用减弱,该位置处压力损失随之减小[9-11]。
笔者所研究的轴入导锥式水力旋流器是在原有的双锥型水力旋流器的基础上,变双切向入口为轴向入口,增加螺旋流道,增加溢流段,取消圆柱段旋流腔,缩小底流管直径,最终确定改进后的旋流结构,不仅实现了紧凑及小型化的目的,而且该结构更适合在井下等狭长空间工作。重点分析了分流比和入口速度对旋流分离器分离性能的影响,同时借助试验对模拟结果进行了验证,所得结论可为该型旋流器的现场应用提供参考。
1 结构及分离原理轴入导锥式水力旋流器结构如图 1所示。研究基于蒋明虎等以往优化设计的单锥型油水两相分离旋流器[12]。为了控制结构的径向尺寸,把切向入口改为轴向入口,来液经螺旋流道进行增速,并在旋流器螺旋流道上方设置引流段,引流段内部采用锥状体便于引流,一方面来液加速进入螺旋流道入口,保证了旋流器的处理量。另一方面起到稳流的作用,保障新型旋流器的分离效率。该水力旋流器的主要结构尺寸包括主直径D、旋流腔长度L1、溢流口直径Du、溢流口深入长度Lu、螺旋流道长度L2、螺旋流道条数a、螺旋流道圈数b、大锥段角度α、小锥段长度L3、小锥段角度θ、底流口直径Dd、底流口长度L4,总长度L。
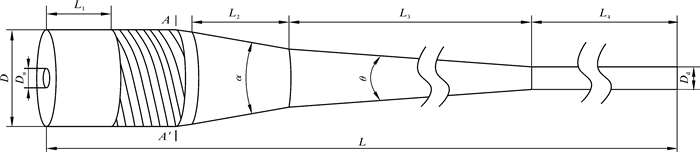
|
| 图 1 轴入导锥式水力旋流器结构示意图 Fig.1 Structural schematic of the axial guide cone hydrocyclone |
旋流器的主要结构参数设置以及模型尺寸如表 1所示。
| 参数 | D/mm | L1/mm | Du/mm | L2/mm | α/(°) | L3/mm | θ/(°) | Dd/mm | L4/mm | L/mm |
| 数值 | 60 | 30 | 12 | 50 | 20 | 535 | 5 | 14 | 500 | 1 165 |
轴入导锥式水力旋流器工作时,油水混合来液从轴向入口进入,经过螺旋流道增压加速,沿螺旋形通道向底流口方向运动,形成连续涡流推动液体边旋转边向圆锥段运动,由于水力旋流器的内径逐渐缩小,使液体的旋转速度加快。液体产生涡流运动时,沿径向的压力不等,靠近轴线附近的压力最低,形成低压区,而在旋流器边壁处的压力最高。促使不互溶混合相中密度较大的油相聚集在分离器的轴心,最终通过上端溢流管排出,密度较大的水相在液流的推动下沿底部底流口排出分离器,从而实现油水两相分离。
2 数值计算 2.1 网格划分在对轴入导锥式水力旋流器进行数值模拟时,首先进行网格划分,如图 2所示,创建结构化网格,划分之后得到188 520个网格。

|
| 图 2 模型的网格划分图 Fig.2 Meshing of the model |
2.2 参数设置
计算时采用混合相模型,主相水密度998.2 kg/m3,油相密度870 kg/m3,动力黏度0.046 1 Pa·s,湍流黏度模型采用雷诺应力模型,多相流模型选择混合物模型[13-14]。入口含油体积分数2%,油滴粒径0.3 mm,溢流口和底流口为自由出口,假设壁面不可渗漏、无滑移,利用壁面函数方程计算剪切应力和近壁处的湍动能和湍流扩散率,残差精度设置为1×10-6[15]。
在模拟过程中,主要分为2大部分,首先,在入口速度不变的情况下,依次改变分流比,对溢流分流比分别为5%、10%、15%、20%、25%、30%和35%时进行数值模拟,根据模拟结果确定最佳分流比。然后,在讨论入口速度对分离效率的影响时,溢流分流比不变,对入口速度分别为0.6、1.2、1.8、2.4和3.0 m/s时旋流器的油相分布情况进行模拟,根据模拟结果确定最佳入口流速。
2.3 模拟结果与分析模拟运算结果收敛,在对不同参数得到的模拟运算结果进行分析时,想通过分析溢流口油相分布来分析分离效率,故选取处于螺旋流道下方的截面A-A′(见图 1) 为研究对象,在该横向截面上对油相体积分数进行分析和对比。图 3所示为截面A-A′示意图。
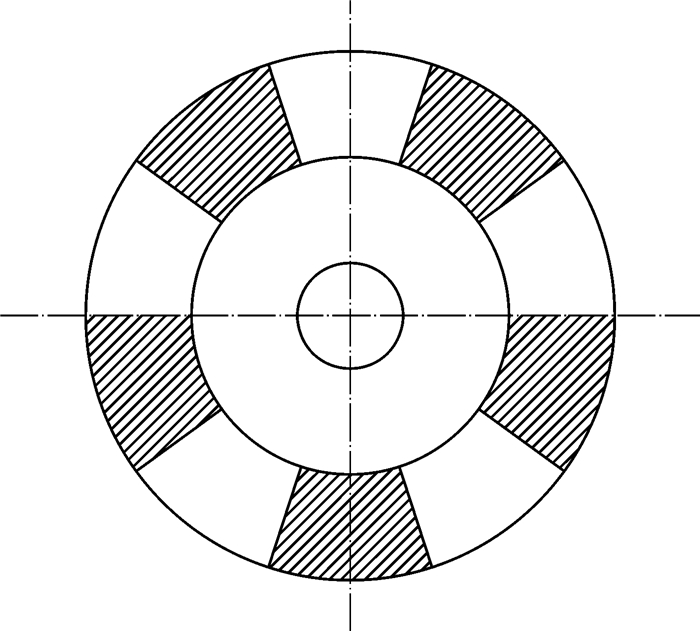
|
| 图 3 截面A-A′示意图 Fig.3 Schematic diagram of Section A-A′ |
2.3.1 分流比对分离性能的影响
分流比f是水力旋流器的一个重要操作参数,它反映了水力旋流器2出口之间流量的分配关系[16]。在研究分流比对轴入导锥式水力旋流器分离性能的影响时,首先将速度以及其他边界条件等参数固定,入口速度定为1.8 m/s,设置溢流分流比,在分流比f分别为5%、10%、15%、20%、25%、30%和35%时进行模拟计算。图 4为不同溢流分流比时旋流器内截面A-A′油相体积分数分布云图。

|
| 图 4 不同分流比时油相体积分数分布云图 Fig.4 Distribution of oil phase volume fraction at different split ratios |
从图 4可以看出,随着分流比的增加,截面中心的颜色呈现出先逐渐变深后变浅的趋势,也就是说,随着分流比的逐渐增大,分离效果逐渐增强,当分流比为0.15和0.20时,图中心的油核聚集较为明显,随着分流比继续增加,油核聚集量减少,图中截面中心色彩显示较弱。可见,当分流比为0.05时,分离效果在所取分流比区间内最差。
图 5为油相体积分数随分流比变化曲线。由图可知,当溢流分流比在0.15~0.25之间时,结构的分离效果较好,当分流比为0.20时,分离效率最高,此时旋流器分离效率为95.0%,随着溢流分流比的继续增加,分流效率逐渐下降。
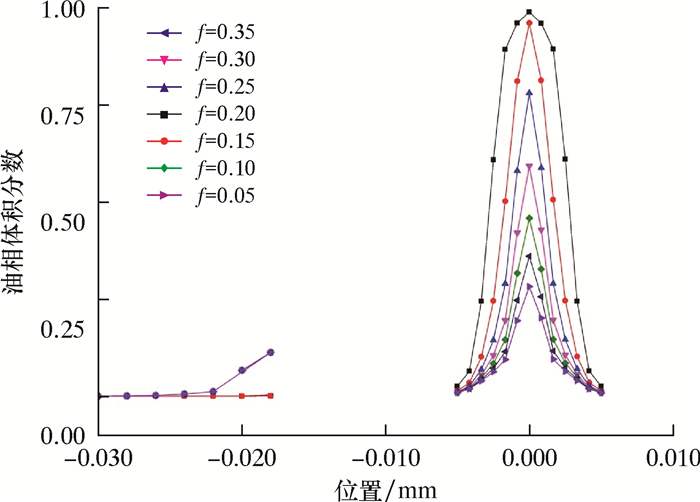
|
| 图 5 不同分流比时油相体积分数分布曲线 Fig.5 Distribution curve of oil phase volume fraction at different split ratios |
2.3.2 入口速度对分离性能的影响
在对不同入口速度进行模拟讨论时,把分流比定为20%,得到的油相体积分数分布云图如图 6所示。
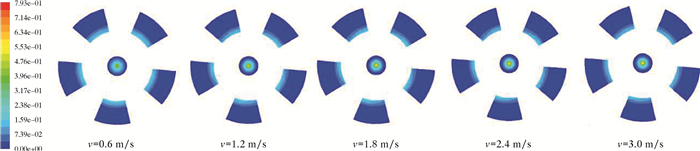
|
| 图 6 不同入口速度时油相体积分数分布云图 Fig.6 Distribution of oil phase volume fraction at different inlet velocities |
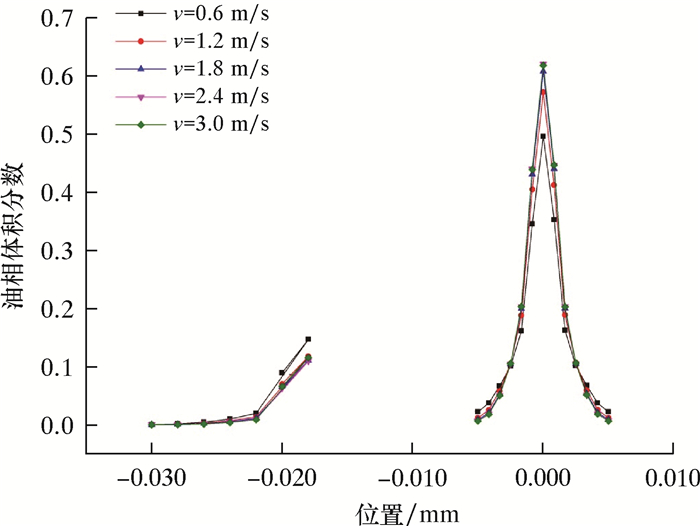
从图 6可以看出,在其他条件一致的情况下,随着速度的增加聚集在轴中心的油相随之增多,也就是说,在速度从0.6 m/s增加到3.0 m/s的过程中,分离效率随之升高,当速度达到1.8 m/s时,在截面A-A′中心的油相分布达到最多。因此,在一定速度范围内,随着速度的增加旋流器中心的油核聚集增多,分离效率随之升高。图 7为不同速度下油相体积分数分布曲线图。
|
| 图 7 不同入口速度时油相体积分数分布曲线 Fig.7 Distribution curve of oil phase volume fraction at different inlet velocities |
由图可知,在分流比固定时,随着速度的增加,一定范围内油相体积分数随之增加。当速度增大至3.0 m/s时,油相体积分数值最大,即分离效果最好。当速度分别为1.8、2.4和3.0 m/s时,三者的油相体积分数值接近重合,也就是说,随着速度的不断增大,旋流器的分离效率不再随之升高。经计算,分离效率最高为95.3%。
3 现场试验 3.1 现场工艺流程为进一步对轴入导锥式水力旋流器的模拟计算结果进行验证,开展了相关试验。试验系统的工艺流程如图 8所示。采油井通过潜油电泵将采出液举升到地面,再经井口出油管线进入试验工艺。根据之前模拟选定的入口速度以及该旋流结构的入口面积进行计算,旋流器分流比控制在5%~35%之间,入口流量控制在5.8~29.2 m3/h之间。试验方案如下:

|
| 图 8 试验系统工艺流程图 Fig.8 Process diagram of the testing system |
(1) 确定最佳分离比。首先将入口流量固定在17.5 m3/h,然后将分流比按5%到35%逐渐设置,对比不同分流比时的分离效率,确定分离效率最高时的溢流分流比。
(2) 确定最佳入口流量。将水力旋流器试验分流比固定在f=20%,将入口流量按照5.8 m3/h到29.2 m3/h逐渐调节,确定分离效率最高时的入口流量。
(3) 将模拟中得到最佳分流比及最佳入口流量与试验所得结果进行对比,观察2种方法所得变化规律是否一致。
3.2 试验结果处理通过对3组不同旋流器、2口不同含水体积分数高含水井入口和出口样品的含油体积分数进行测试,完成了模拟结果和试验结果的对比分析。为了减少随机误差对结果造成的不良影响,每个测试结果采集多组样液进行测试。使用含油分析仪测量混合液含油,并换算成含油体积分数,进而计算出分离效率。分离效率采用的是综合效率的计算方法[17],计算公式为:

|
(1) |
式中:K为仅与入口含油体积分数有关的常数,等于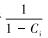
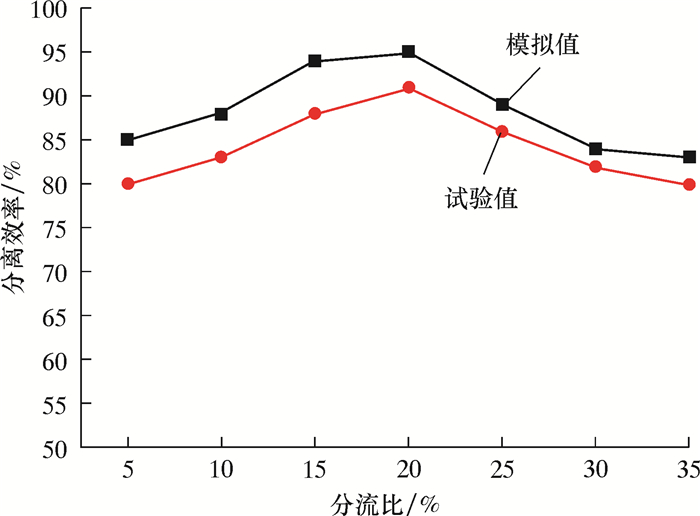
图 9为分离效率试验值与模拟值的对比曲线。由图可以看出,分离效率与分流比关系密切,虽然模拟值和试验值有一定的偏差,但总的来说,试验结果与模拟结果比较接近。该结构的最优分流比为20%,分流比过小或者过大都不利于旋流分离。
|
| 图 9 分离效率随分流比变化的试验值与模拟值对比曲线 Fig.9 Experimental and simulated comparison curves of separation efficiency versus split ratio |
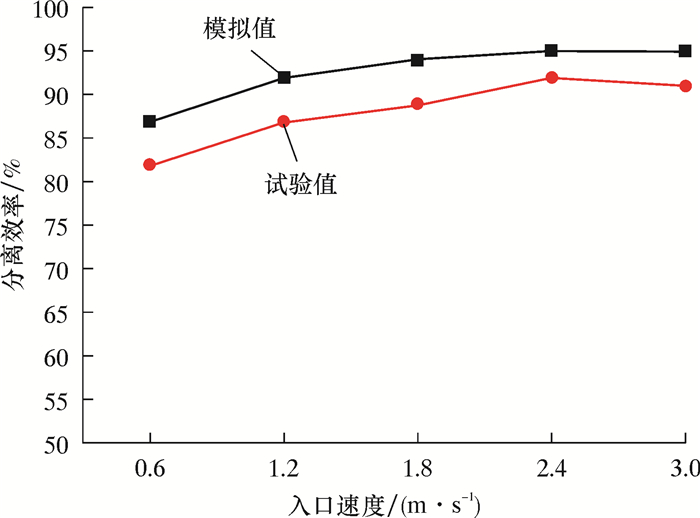
图 10为分离效率随入口流量变化曲线。流量用入口速度表示,由图可知,在一定范围内,随入口速度的增加,分离效率不断升高,但当速度增大到3 m/s时,分离效率随入口流量增加而逐渐降低,最佳入口速度位于1.8~2.4 m/s之间。由此可以看出,对于结构固定的水力旋流器,在一定范围内随着入口流量增加其分离效率随之升高,由于结构尺寸限制,其处理量有限,过大的处理量将会造成过大的压力损失,同时使液体进入旋流器的速度过高,可能导致液体破碎,不利于分离。处理量过低会使得液流进入旋流器的流速大幅度下降,不能形成强度足够的涡旋,对分离也非常不利。因此,任何一个结构固定的旋流器都有一个合理的流量处理范围。
|
| 图 10 分离效率随入口流量变化的试验值与模拟值对比曲线 Fig.10 Experimental and simulated comparison curves of separation efficiency versus inlet flow rate |
4 结论
(1) 通过分析数值模拟计算和现场试验结果可知,随着分流比的增加,轴入导锥式水力旋流器的分离效率呈现出先逐渐升高后降低的趋势,当分流比为20%时,分离效果最好,现场试验的分离效率可达到91.5%。
(2) 轴入导锥式水力旋流器在一定的范围内,随入口速度的增加分离效率升高,当入口速度达到2.4 m/s时,试验分离效率达到92.0%。
| [1] | 赵立新, 徐磊, 陈世琢, 等. 尾管过滤式水力旋流器滤出效率实验研究[J]. 化工机械, 2008, 35(5): 267–270. |
| [2] | 徐保蕊, 蒋明虎, 刘书孟, 等. 分流比对旋流器油水分离性能影响的模拟研究[J]. 化工机械, 2015, 42(3): 399–403. |
| [3] | 牛贵锋, 艾志久, 刘春全, 等. 油水旋流分离器数值模拟优化研究[J]. 石油钻采工艺, 2008, 30(3): 71–74. |
| [4] | 牛贵锋, 艾志久, 刘春全. 油水分离旋流器的模拟分析与结构优化[J]. 钻采工艺, 2008, 31(6): 102–105. |
| [5] | 赵立新, 刘丽丽, 徐磊, 等. 倾斜入口流道的水力旋流器数值模拟分析[J]. 化工机械, 2012, 39(2): 203–205. |
| [6] | 艾志久, 贺会群, 牛贵锋, 等. 油水旋流分离器入口结构优化研究[J]. 石油机械, 2007, 35(1): 5–7, 32. |
| [7] | 蒋明虎, 李永山, 徐保蕊, 等. 轴流式脱气除砂三相旋流分离器操作参数优选[J]. 化工机械, 2015, 42(1): 68–71, 153. |
| [8] | 赵立新, 宋民航, 蒋明虎, 等. 轴流式旋流分离器研究进展[J]. 化工机械, 2014, 41(1): 20–25. |
| [9] | 俞接成, 陈家庆, 韩景. 轴向入口油水分离水力旋流器及其数值模拟[J]. 北京石油化工学院学报, 2009, 17(2): 19–23. |
| [10] | 赵传伟, 李增亮, 董祥伟, 等. 井下双级串联式水力旋流器数值模拟与实验[J]. 石油学报, 2014, 35(3): 551–557. DOI: 10.7623/syxb201403018 |
| [11] | 蒋明虎, 赵立新, 李枫, 等. 旋流分离技术[M]. 哈尔滨: 哈尔滨工业大学出版社, 2000. |
| [12] | 蒋明虎, 陈世琢, 李枫, 等. 紧凑型轴流式除油旋流器模拟分析与实验研究[J]. 油气田地面工程, 2010, 29(9): 18–20. |
| [13] | 赵立新, 朱宝军. 不同湍流模型在旋流器数值模拟中的应用[J]. 石油机械, 2008, 36(5): 56–60. |
| [14] | 琚选择, 李自力, 孙卓辉, 等. 液-液水力旋流器两相湍动流数值模拟研究进展[J]. 化学工业与工程, 2009, 26(1): 84–90. |
| [15] | 赵立新, 朱宝军, 李凤明. 离心式气液分离器内流场的数值模拟与结构优化[J]. 化工机械, 2007, 34(2): 90–94. |
| [16] | 袁惠新, 俞建峰, 刘宏斌. 分流比对油水分离旋流器基本性能的影响[J]. 石油机械, 2000, 28(9): 17–19. |
| [17] | 倪玲英, 王剑. 液-液旋流器分流比特性系数研究[J]. 过滤与分离, 2001, 11(1): 19–20, 37. |




