0 前言
张力腿平台(TLP)是深海顺应式平台的一种典型形式[1],它不仅垂荡运动较小[2],且控制方向上的张力可以牵制非控制方向的运动,在波浪中运动性能较好,能抵抗恶劣的海洋环境,因此TLP成为深海采油平台的主要形式之一[3]。
张力腿平台的整体结构强度和水动力分析计算一般采用SEASAM等软件进行整体建模[4]。单独就张力腿平台某一上部模块进行结构有限元分析时,张力腿平台的运动对上部模块产生的影响是研究的重点之一[5]。对导管架平台的上部模块进行有限元分析均采用静力分析方法[6],而张力腿平台必须考虑平台水平运动加速度(X和Y方向)和垂直运动加速度(Z方向)对上部钻井模块等的影响[7]。
笔者使用SEASAM软件对张力腿平台进行水动力分析计算,获得各个波浪频率和不同浪向下平台的极值加速度和加速度时程曲线。使用有限元分析软件ANSYS建立张力腿平台的上部钻井支持模块(Drilling Support System,DSM),结合水动力分析计算得到加速度,通过对比分析论证准静力方法的合理性,最后使用准静力方法对各工况下的钻井支持模块进行结构有限元分析。
1 张力腿平台水动力分析计算笔者采用SEASAM软件对TLP进行水动力分析计算,在GeniE模块中建立TLP的几何模型并进行湿表面网格划分,在HydroD模块中建立水动力计算模型,定义TLP质量模型,对波浪载荷、运动响应进行分析计算,得到TLP的加速度响应谱。
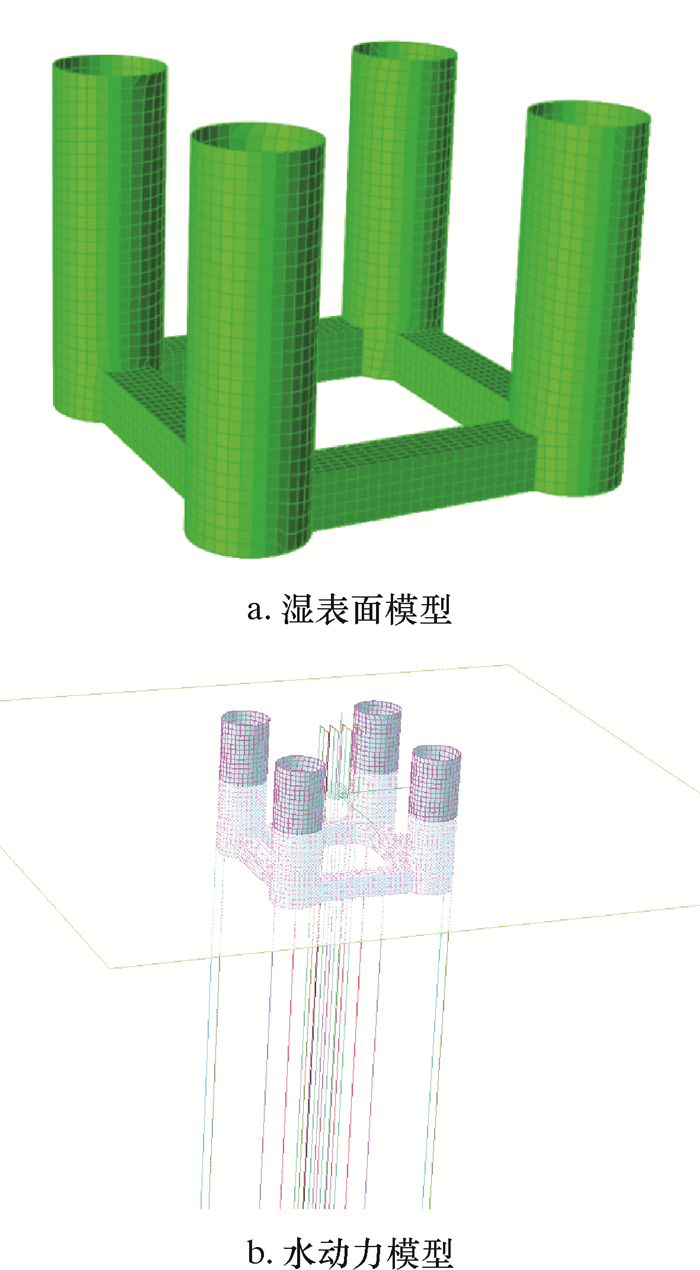
1.1 张力腿平台模型TLP的船体结构采用Panel单元模拟,张力腿筋键和立管采用Morison单元模拟[8],根据莫里森方程计算波浪力。考虑正常作业、不可预期和极端风暴等3种不同的工况。TLP的船体湿表面模型、张力腿筋键的水动力模型如图 1所示(以正常作业工况为例)。
|
| 图 1 张力腿平台水动力模型 Fig.1 Hydrodynamic model of tension leg platform |
1.2 张力腿平台的加速度
在HydroD中基于三维势流理论[9]可计算得到平台运动响应幅值RAO。将6个自由度方向的加速度仅转化为X、Y、Z3个自由度方向的线性加速度,由转化公式可得平台3个方向的加速度传递函数,再输入波浪谱,可计算各波浪入射角度的加速度响应谱。由加速度谱可以进一步得到平台运动的极值加速度和加速度时程曲线。
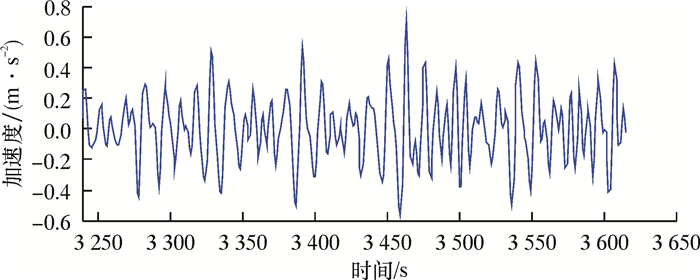
通过计算可知,Z向加速度可忽略不计。以正常作业工况波浪0°入射为例,其Y向加速度时程曲线如图 2所示,Y向加速度极值为0.783 m/s2。
|
| 图 2 正常作业工况波浪0°入射Y向加速度时程曲线 Fig.2 Time history curve of Y-direction acceleration of the wave with 0° incident under normal operating conditions wave |
2 钻井支持模块有限元模型和加载 2.1 DSM有限元模型
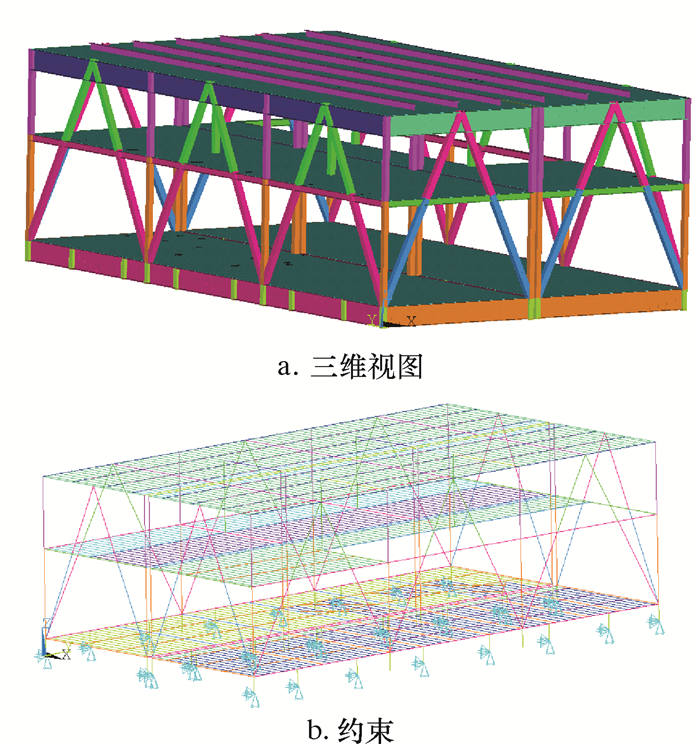
DSM是一个3层的矩形框架式结构,四周有垂向和斜向撑杆,为结构提供侧向刚度。DSM模型基于某TLP结构图纸建立,模型由板、主梁、立柱、垂向撑杆和斜撑组成。模型的梁、立柱和撑杆在ANSYS中采用BEAM188单元模拟[10],板结构采用SHELL63单元模拟。DSM有限元模型如图 3a所示。DSM由TLP主甲板进行支撑,DSM基座和TLP主甲板上部结构通过焊接剪切板进行连接,因此DSM边界取在支撑点底部,并使用铰支约束,如图 3b所示。
|
| 图 3 钻井支持模块有限元模型 Fig.3 Finite element model of drilling support module |
2.2 DSM加载
DSM结构载荷包括重力载荷和环境载荷,其中重力载荷依据模型结构图纸和TLP重力控制报告施加,环境载荷依据风载荷和加速度相关数据施加。重力载荷分为静载荷和活载荷。静载荷主要包括结构自重、高压钻井液、泵管子、导管、阀和其他一些设备。活载荷包括钻杆、套管、立管、钻井液、流体(石油、燃料等)和水泥袋等。其中结构钢材自重通过定义构件几何尺寸和钢材密度由程序自行计算得出,其他设备载荷在对应位置节点内采用MASS21单元模拟。环境载荷包括风载荷和惯性载荷。风载荷如表 1所示,设计风速结合业主要求和API 4F规范给出[11]。
风载荷的计算一般基于风压和受风面积。出于分析目的,文中仅考虑受风面积。风载荷根据API 4F 8.3章节中的相关规范进行计算[11]。按照45°的增幅计算0°~360°范围内8个方向的风载荷。通过计算得DSM结构受到的风载荷如表 2所示,其他方向风载荷可根据0°和90°方向受风计算得到,风载荷以节点集中力的形式施加到模型受风面的所有节点上。
| 工况 | 0°方向总受风载荷 | 90°方向总受风载荷 |
| 正常作业 | 470.4 | 499.8 |
| 不可预期 | 1 176.0 | 1 234.8 |
| 极端风暴 | 2 518.6 | 2 646.0 |
风、流和波浪力引起TLP运动会导致上部模块和设备产生惯性载荷,通过加速度响应谱可以进一步计算得到平台运动的加速度极值及加速度时程曲线,据此可以考虑不同环境惯性载荷对结构产生的影响。该载荷在ANSYS中以定义惯性力的方式实现加载。
其他载荷的加载保持不变,仅惯性载荷按照不同的方式加载,对DSM结构进行静力分析、准静力分析和动力时程分析。其中,静力分析不施加惯性载荷,即不考虑平台运动对上部结构产生的影响;准静力分析在Gravity中输入横向加速度极值,即以加速度极值来近似地考虑平台运动对上部结构的影响;动力时程分析则输入加速度时程曲线,输入方法类似准静力分析,只是由于加速度随时间变化,所以要选取合适的时间间隔,输入多组数据。
3 钻井支持模块结构分析方法比较以正常作业工况风载荷和惯性载荷90°入射为例,静力分析时不考虑惯性载荷;准静力分析时Y方向加速度为-0.783 m/s2;动力时程分析以1 s为间隔,输入300 s对应波浪(如图 2所示)的加速度时程曲线。
甲板间撑杆上的节点1和2主要受环境载荷影响,因此X和Y方向位移较大,据此可以考量平台运动对X和Y方向位移的影响。3层甲板上的节点3、4和5主要受重力载荷影响,Z向位移较大,X和Y向位移几乎可以忽略不计,据此可以考量平台运动对结构Z向位移的影响。位移计算结果如表 3所示。表中静力分析和准静力分析的误差都是相对动力分析结果。
| 节点 | 节点位置 | 方向 | 静力位移/ cm |
准静位移力/ cm |
动力位移/ cm |
静力分析误差/ % |
准静力分析误 差/% |
| 1 | 甲板间撑杆 | UX | 2.906 | 3.135 | 3.164 | 8 | 1 |
| 2 | 甲板间撑杆 | UY | 2.236 | 3.300 | 3.084 | 27 | 7 |
| 3 | 上层甲板 | UZ | -1.451 | -1.451 | -1.471 | 1 | 1 |
| 4 | 中层甲板 | UZ | -3.344 | -3.429 | -3.441 | 3 | 0 |
| 5 | 下层甲板 | UZ | -0.724 | -0.724 | -0.724 | 0 | 0 |
由表 3可知,动力时程分析存在一定的动力放大效应,惯性载荷对X和Y方向位移影响较大,对于节点1和2,准静力分析结果误差更小。惯性载荷对Z向位移影响较小,对于节点3、4和5,准静力分析结果误差仍较小。
动力时程分析方法与现实接近,但计算量较大,耗费时间过长,准静力分析方法既避免了动力分析的巨大计算量,又能得到更符合实际的计算结果,因此选择准静力分析方法对DSM进行结构有限元分析。
4 钻井支持模块准静力分析DSM的准静力分析有正常作业工况、不可预期工况和极端风暴工况。每种工况下的环境载荷都有8个不同的作用方向,因此对DSM一共进行24种不同工况组合下的准静力分析。为了详细描述分析结果,将板结构分为上层甲板、中层甲板和下层甲板,分别提取24种情形下各层甲板的最大等效应力和最大变形,并对梁结构进行分组,提取24种情形下各个梁结构的最大等效应力。
4.1 板结构强度DSM板结构安全裕量较大。3层甲板的最大等效应力值、发生位置、对应工况及板材屈服极限如表 4所示(以正常作业工况为例)。
| 位置 | 最大等效应力/MPa | 发生位置 | 对应工况 | 屈服极限/MPa |
| 上层甲板 | 64.05 | 甲板与斜撑相交处 | 极端风暴0°入射 | 235 |
| 中层甲板 | 114.47 | 甲板与侧向支撑骨材相交处 | 极端风暴315°入射 | 235 |
| 下层甲板 | 125.38 | 甲板与侧向支撑骨材相交处 | 极端风暴0°入射 | 235 |
对比3层板的最大等效应力可知,中层和下层甲板的应力较大,上层甲板相对较小。其原因是由于上层甲板为10 mm厚的板,比其余2层板更厚,且上层甲板骨材多采用高腹板的工字形钢材,对上层甲板起到了良好的支撑作用。对比最大等效应力发生的位置可知,DSM板结构应力计算结果较大的位置主要为应力集中处,而有限元模型中对这些结构局部细节进行了简化,因此结构的实际应力低于计算值,可以认为结构实际强度储备更大,可以适当考虑减小板厚,节省用钢。
4.2 梁结构强度DSM骨材最大等效应力为179.67 MPa,安全裕量较大。其中几组等效应力较大的骨材应力计算结果如表 5所示。由表可知,G17型号骨材应力较大,这是因为中层甲板承受设备载荷与活载荷;大梁I1位于上甲板管子堆场下部,是结构关键骨材之一,承受的重力载荷较大;B4型号的方管为DSM结构撑杆,受轴向载荷与风载荷联合作用影响较大。对于等效应力较小和跨距较短的次要构件可以考虑适当优化。
| 骨材编号 | 位置 | 最大等效应力/MPa | 对应工况 | 屈服极限/MPa |
| G17 | 中层甲板 | 179.67 | 极端风暴工况0°入射 | 355 |
| I1 | 上甲板管子堆场下部 | 138.20 | 极端风暴工况0°入射 | 355 |
| B4 | 甲板间竖直撑杆 | 164.54 | 极端风暴工况225°入射 | 355 |
4.3 整体变形
DSM 3层甲板位移云图如图 4所示,其中标红处是最大位移发生位置。从3层板X、Y、Z 3个方向位移来看,Z方向位移最大,这是因为重力载荷对结构位移影响较大。从3种工况来看,极端风暴工况下位移最大,这是由于3种工况的重力载荷相差不大,环境载荷对结构位移影响较大。甲板最大位移发生在中层甲板上,为3.49 cm,甲板变形的安全裕量较大。从最大位移发生位置来看,各个工况分析结果类似,即上层甲板最大位移发生在管子堆场下部,中层甲板最大位移发生考虑上部零散设备较多的位置,下层甲板最大位移发生在钻井泵放置的位置,这都由重力载荷较大引起。

|
| 图 4 钻井支持模块甲板位移云图 Fig.4 Deck displacement of drilling support module |
5 结论
(1) 通过水动力分析计算,得到张力腿平台X 、Y和Z 3个方向的极值加速度和加速度时程曲线,可以将它们以惯性载荷的形式,分别作为平台上部DSM结构准静力分析和动力时程分析的输入数据。
(2) 通过DSM结构静力分析、准静力分析和动力时程分析的对比,得出准静力分析方法既避免了动力分析的巨大计算量,又比静力分析能得到更符合实际的计算结果,因此准静力分析方法具有合理性和工程实用性。
(3) 通过对DSM结构进行各工况下的准静力分析计算,得出DSM板结构和梁结构的强度及整体变形均满足要求,并对受力较小的板结构和梁结构提出了优化建议。
| [1] | 段梦兰, 李秀巧, 赵秀菊, 等. 发展张力腿平台迎接深水钻井的挑战[J]. 石油机械, 2000, 28(12): 46–48. |
| [2] | AHMAD S K, AHMAD S. Active control of non-line-arly coupled TLP response under wind and wave environments[J]. Computers and Structures, 1994, 72(6): 735–747. |
| [3] | 张智, 董艳秋, 唐友刚, 等. 1990年后世界TLP平台的发展状况[J]. 中国海洋平台, 2004, 19(2): 5–11. |
| [4] | 国家863计划"典型深水平台概念设计研究"课题组. 张力腿平台结构总体强度分析研究[C]//2005年度海洋工程学术会议论文集. 上海: 中国造船工程学会近海工程学术委员会, 2005. |
| [5] | 杨春晖, 董艳秋. 深海张力腿平台发展概况及其趋势[J]. 中国海洋平台, 1997(6): 255–258. |
| [6] | 祖巍. 流花油田张力腿平台模块钻机结构设计研究[J]. 石油机械, 2017, 45(1): 58–61. |
| [7] | 徐田甜, 张建勇, 王宁. 西江23-1油田海洋模块钻机结构设计[J]. 船舶, 2006(5): 26–32. |
| [8] | "典型深水平台概念设计研究"课题组. 张力腿平台水动力响应分析[J]. 中国造船, 2005, 46(增刊1): 477–489. |
| [9] | NEWMANN J N. 船舶流体动力学[M]. 周树国, 译. 北京: 人民交通出版社, 1986. |
| [10] | 杨树耕, 孟昭瑛, 任贵永. 有限元分析软件ANSYS在海洋工程中的应用[J]. 中国海洋平台, 2000, 15(5): 41–44. |
| [11] | ANON. Specification for drilling and well servicing structure:API SPEC 4F[S]. Washington:API Publisher, 1995. |




