0 引言
在连续管水平钻井中,管柱与井壁之间的摩阻是影响钻井深度的重要因素[1-3]。相关研究人员采取了很多措施来减小摩阻[4-7],也研究了很多种用于连续管的井下减阻器[8-16]。笔者通过对国内外各种减阻器的比较分析,选定机械式振动减阻器为研究对象,用有限元软件设计了井下减摩振动器的具体结构。抽取流体域模型并将其导入到ANSYS Fluent流体软件中,模拟计算出振动过程中液体压力随阀口间隙的变化规律,据此关系计算并选出2个碟形弹簧的特性参数;最后将相关参数植入用Simulink模块建立的振动仿真系统中,计算了整个振动过程中减阻器各参数随时间的变化规律。以期为类似振动减阻器的设计提供参考。
1 振动器流体的模拟 1.1 井下振动减阻器的结构M.L.CONNELL和A.M.FERGUSON提出了机械式振动减阻器[2](见图 1,不包括9号缓振碟簧)。笔者根据其原理[17-19]设计出较合理的尺寸,并在此基础上进行优化(加入了缓振碟簧),得到如图 1所示的详细结构示意图。

|
| 图 1 振动工具结构示意图 Fig.1 Structural schematic of vibration tool 1—上接头; 2—外筒; 3—卡阀; 4—通阀; 5—阀杆盘; 6—上碟簧; 7—振动管; 8—节流阀; 9—缓振碟簧; 10—阀杆; 11—活塞; 12—心轴; 13—振动下端; 14—振动体; 15—下碟簧套筒; 16—下碟簧; 17—下接头。 |
钻井液从减阻器上接头前端口流入,通过节流阀的节流孔后压力下降,形成一定压差,压缩上碟簧,推动阀杆靠近振动组前端的活塞。随着阀杆的靠近,活塞口的间隙越来越小,流出液体也会越少,活塞前部的腔体憋压,压力越来越大,当该压力大于下碟簧的弹力后开始推着振动组和阀杆一起向前运动。两碟簧弹力随着位移逐渐增大,在阀杆没有脱离之前,两者一起运动的加速度一直减小,当上碟簧的弹力大于液体推力时,两者开始分开,当其间隙被拉开后,压力快速释放,两运动部件也迅速反弹。阀杆会冲击缓振弹簧,而振动组则直接撞到振动下端,使撞击力传到钻柱,产生轴向振动。阀杆撞击的能量被弹簧储存并释放,随着钻井液循环,阀杆在弹力和液体力作用下重新靠近活塞,产生持续周期性振动。
井下减摩振动器的应用效果与工作频率和冲击力有关,地面泵的最大流量通常固定,振动器的频率和冲击力只与其设计参数有关。轴向振动器的工作频率一般为12~26 Hz[20],具体振动频率取决于工具参数和工况。
采用试错法确定井下减摩振动器的参数。首先确定振动器的尺寸,然后检验其功能,再调整振动器的参数,直至达到设计目的。
根据实际工作情况取输入流量Q=400 L/min,活塞行程S=30 mm。以此作为已知量来模拟其工作频率是否满足要求,并计算最大冲击力。
1.2 流体域模型振动过程中主要是利用钻井液的能量来循环作业,为了模拟整个振动过程,计算出振动频率,这就需要知道振动过程中压力的变化。笔者利用ANSYS Fluent模块模拟计算振动过程中流体的压力变化。
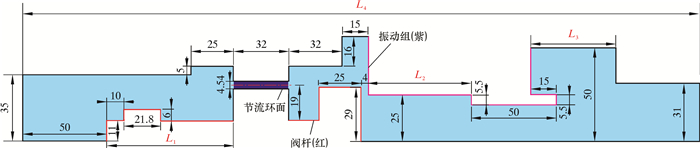
从图 1可以截取出用于模拟分析的流体域模型,但整个模型太复杂,也没有针对性,因此需要对该流体域模型进行简化。模拟中主要看2个运动部件(阀杆和振动组)的运动关系,因此取出图 1中间段并排除碟簧体积的影响,模型如图 2所示。
|
| 图 2 流体域模型 Fig.2 Fluid domain model |
取出的流体域除节流孔部分外其他部分都呈轴对称,为了加快计算速度,将三维模型简化为二维平面模型。等效的简化节流孔为节流环面(见图 2蓝色区域),保持环形面的中心与原节流孔的圆心不变。因节流是通过控制面积来降压,所以面积上需要相等。设环形面的宽度为k,原节流孔总面积S1=nπr2,简化模型后面积S2=πRw2-πRn2,其中n=9, 表示节流孔个数;r=5.5, 为单个节流孔半径(n, r和圆心位置由结构设计得到);Rw=30+k/2, 为节流环面外半径;Rn=30-k/2为节流环面内半径。因S1=S2,所以可得k=4.54 mm。
1.3 流体的模拟利用有限元软件建立网格化模型,导入到ANSYS Fluent中设置好计算参数。因有2个运动边界,所以在前处理中需要设置动网格参数,并加载自定义运动速度的udf文件。运动边界的速度与实际受力相关,但刚开始碟簧还不能确定,而液体压力只与流体腔道有关联,故分别给定2运动边界一个线性变化的速度,阀杆边界速度比振动组边界速度大,使2边界相互靠近,直到接触后停止。取出运动过程中的压力差做数据分析。
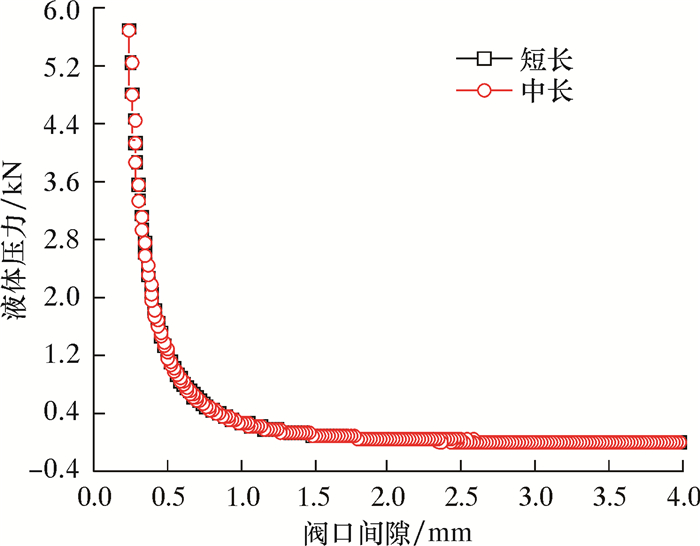
为了确保简化后的模型不影响计算结果,笔者设计了几组不同长度的模型(见表 1) 代入计算压力差(阀口高度h=25 mm),计算结果如图 3~图 5所示。
| 模型 | L1 | L2 | L3 | L4 |
| 短长 | 75 | 61 | 50 | 400 |
| 中长 | 125 | 111 | 100 | 550 |
|
| 图 3 阀杆上不同长度的压力差 Fig.3 Pressure differences of stem under different lengths |
|
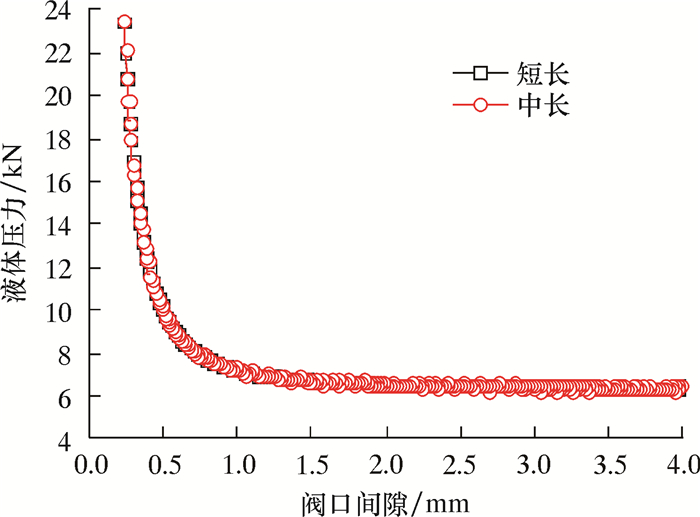
| 图 4 振动组不同长度的压力差 Fig.4 Pressure differences of vibration groups under different lengths |
|
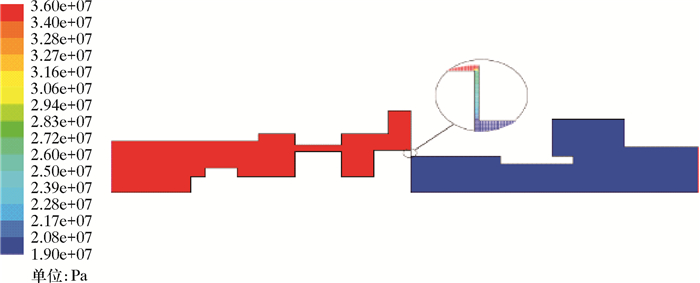
| 图 5 间隙0.22 mm下的压力分布云图 Fig.5 Pressure distribution in the 0.22 mm gap |
从图 3可以看到2不同长度运动部件上的压力差几乎重合,说明长度对此模型没有多大影响,故将模型简化为短长模型长度可行。图 5是短长模型间隙0.22 mm下的压力分布云图。
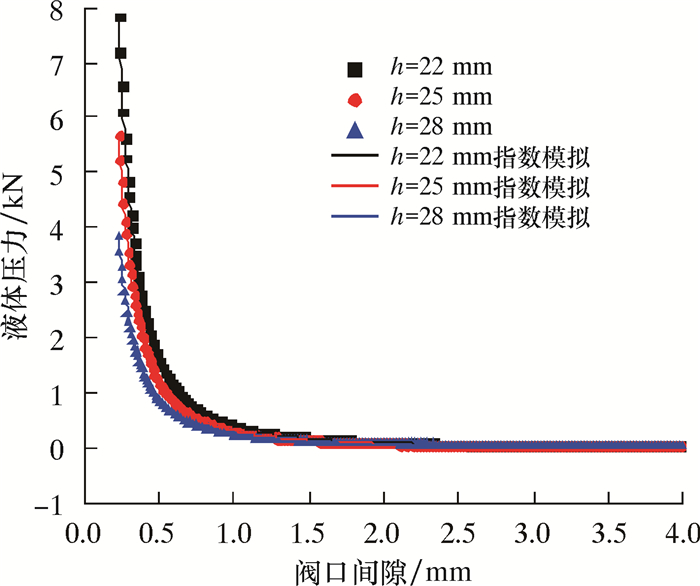
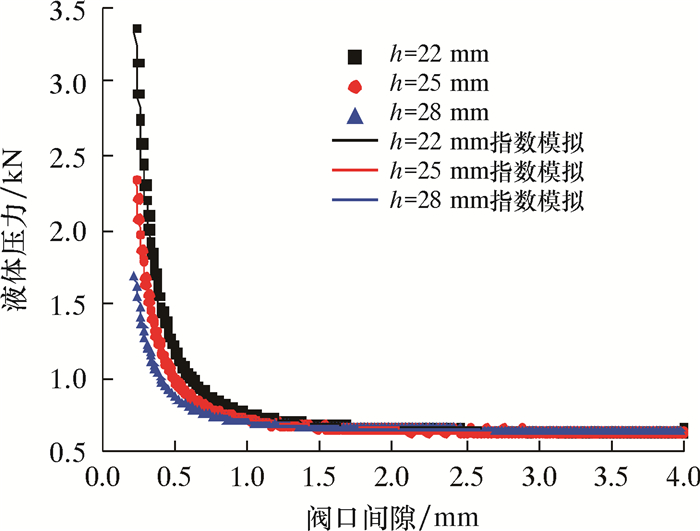
简化后的模型阀口高度和间隙是影响液压的主要因素,因此分别就阀口高度22、25和28 mm从间隙4 mm开始运动模拟分析压力变化。将取出的数据放到Origin中处理,发现用指数函数可以很好地拟合数据点,结果如图 6和图 7所示。拟合得到2个运动件前、后压力差随间隙变化的曲线方程:
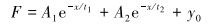
|
(1) |
|
| 图 6 阀杆前、后压力差随间隙变化曲线 Fig.6 Pressure difference before and after the stem versus the gap |
|
| 图 7 振动组前、后压力差随间隙变化曲线 Fig.7 Pressure difference before and after the vibration group versus the gap |
从图 6和图 7可以看出,阀口高度越高,间隙越小,液体压力差越大,这与实际情况相近,可为后续调整参数提供参考;间隙在1.00~0.20 mm之间压力增长非常快。但实际液体压力受到泵安全阀的压力限制,不可能一直增长,间隙0.22 mm时,压力达到36 MPa,与泵的输出压力接近,流体会推着阀杆和振动组一起运动;间隙0.22 mm时,阀杆和振动组所承受的最大液体力分别是5.7和23.5 kN,以此作为上碟簧和下碟簧的最大负载进行下一步设计。
2 碟簧的选择与组合选择碟簧时应使其既能够承受液体压力的压缩,又能在规定位移往复运动一定时间而不致损坏。
一般取A、B、C 3个系列。上碟簧的安装空间可以从机械碟簧标准GB/T 1972—2005中选出3个系列,如表 2所示。
| 上碟簧 | D/mm | d/mm | t/mm | h0/mm | H0/mm | Ff/h0=0.75/kN |
| A45 | 45 | 22.4 | 2.50 | 1.0 | 3.50 | 7.72 |
| B45 | 45 | 22.4 | 1.75 | 1.3 | 3.05 | 3.66 |
| C45 | 45 | 22.4 | 1.25 | 1.6 | 2.85 | 1.89 |
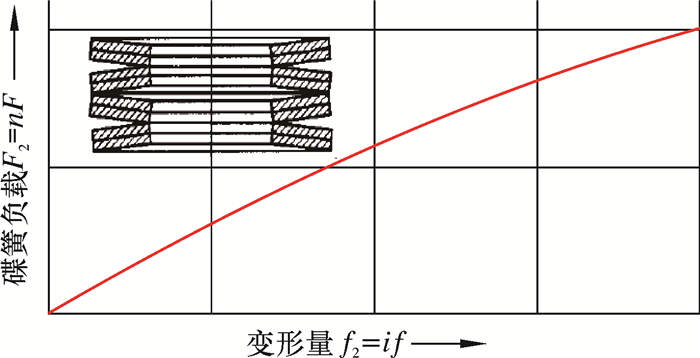
由表 2可见,采用单纯的单片堆叠方式,碟簧太刚硬,并且这样应力幅比较大,会缩短碟簧寿命。为方便安装和检修,尽量选择同种类型的碟簧进行组合。复合组合碟簧的组合方式如图 8所示。
|
| 图 8 复合组合碟簧 Fig.8 Composite disc spring |
2.1 上碟簧的选择及组合
除表 2的参数以外,还有其他一些约束条件:① 上碟簧的安装高度需受工具安装空间限制;② 由图 6设计的碟簧最大负载系数需小于临界值0.75;③ 应力幅越小,碟簧的疲劳寿命越长;④ 上碟簧没有预紧量,但原件肯定会有一定的起步压力,刚开始液体压力应大于上碟簧的起步压力,这样才能推着阀杆向前运动,因此液体的起步压力应大于碟簧的起步弹力,这样才能构成循环振动,即上碟簧的起步压力愈小愈好。上碟簧的取值如表 3所示。
| 系列 | Fc/kN | 总高度/mm | 起步压力/N | 组数 | n片组 | 负载系数fz/h0 | 应力幅/MPa |
| A | 10.04 | 648.00 | 50.68 | 108 | 2 | 0.28 | 569.72 |
| B | 4.48 | 451.95 | 194.43 | 69 | 3 | 0.34 | 572.11 |
| C | 2.01 | 525.95 | 218.49 | 67 | 5 | 0.28 | 555.39 |
从表 3可以看出,A系列的起步压力最小,故选择A系列参数进行组合。这样就选出参数108组、每组2片对合组装的外径45 mm的标准碟簧。用Matlab根据碟簧特性曲线和上碟簧参数拟合出弹力与变形曲线方程:
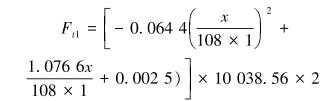
|
(2) |
下碟簧的3种类型如表 4所示。
| 下碟簧 | D/mm | d/mm | t/mm | h0/mm | H0/mm | Ff/h0=0.75/kN |
| A100 | 100 | 51 | 6.0 | 2.2 | 8.2 | 48.0 |
| B100 | 100 | 51 | 3.5 | 2.8 | 6.3 | 13.1 |
| C100 | 100 | 51 | 2.7 | 3.5 | 6.2 | 8.6 |
下碟簧的选择与上碟簧的选择类似,但下碟簧需要预紧力,也就是需要一定的预紧量。安装高度在300~500 mm之间的参数如表 5所示。
| 系列 | Fc/kN | 总高度/mm | 预紧力/kN | 组数 | n片组 | 负载系数fz/h0 | 应力幅/MPa |
| A | 62.72 | 475.60 | 9.5 | 58 | 1 | 0.38 | 544.10 |
| B | 15.85 | 478.80 | 8.0 | 36 | 3 | 0.42 | 454.18 |
| C | 9.09 | 429.00 | 7.7 | 30 | 4 | 0.37 | 528.62 |
从表 5可以看出,在同样的高度下B系列的振幅最小,也就是寿命最持久。如果对寿命要求较高就可以考虑B系列参数;如果安装空间较紧张就选择C系列参数。笔者根据结构空间的限制选择C系列参数。此预紧力下的预紧量x0=8.4 mm,这样选出参数30组、每组4片C系列、外径100 mm的标准碟簧。同样利用Matlab拟合出下碟簧的弹力与变形量的曲线方程:
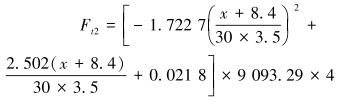
|
(3) |
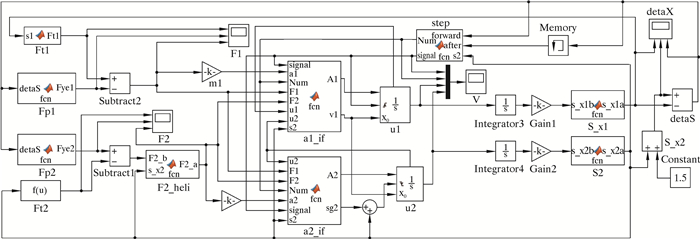
有了各个函数关系,便可用Matlab中Simulink模块建立振动仿真系统来模拟计算往复运动的周期,也就可以确定该工具的振动频率。Simulink振动仿真系统如图 9所示,将最左边的Ft1、Ft2模块分别代入式(2) 和式(3),而将Fp1、Fp2代入式(1)。
|
| 图 9 Simulink振动仿真系统 Fig.9 Simulink vibration simulation system |
由于下碟簧有预紧力,所以F2_heli模块的作用就是控制振动组初始运动合力大于0才开始运动;而上碟簧没有预紧,所以不需要判断。m1、m2分别是阀杆和振动组的质量倒数,将其传送到a1_if和a2_if模块分别是各自的加速度。加速度对时间的积分就是各自的运动速度u1、u2,再次积分就是运动位移S_x1和S_x2(加上初始间隙以同步)。将两者位移之差代到下一次的输入中就可以迭代计算振动的各个状态。
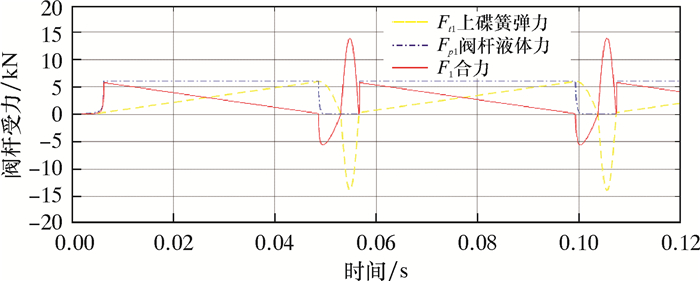
设定模拟时间为0.12 s后进行计算,绘出各参数的变化曲线,结果如图 10~图 13所示。
|
| 图 10 阀杆受力曲线 Fig.10 Force on the stem |
|
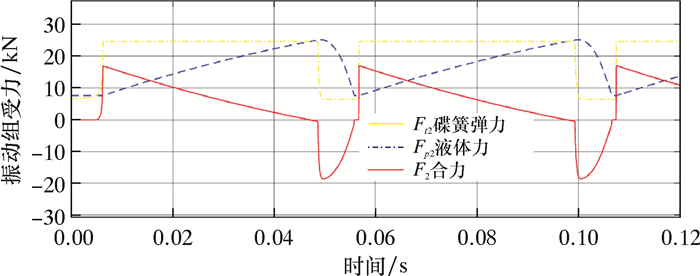
| 图 11 振动组的受力曲线 Fig.11 Force on the vibration group |
|
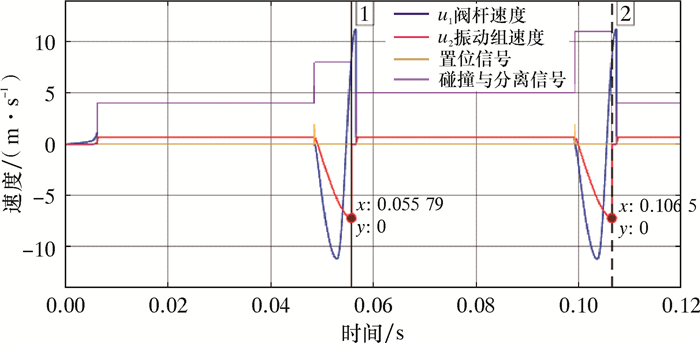
| 图 12 运动部件的速度曲线 Fig.12 The velocity curve of the moving part |
|
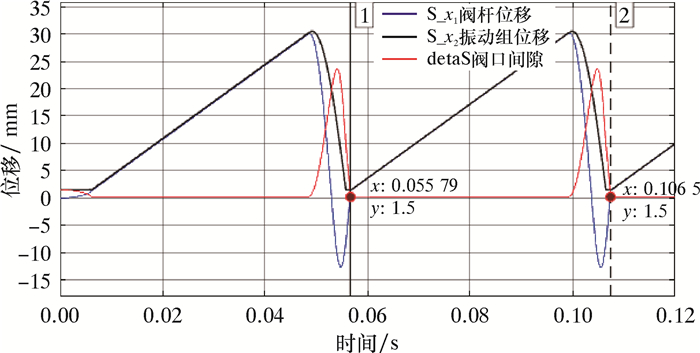
| 图 13 两运动部件的位移与间隙 Fig.13 Displacement and clearance of two moving parts |
从图 10可以看出初始时刻的选择很关键,也就是阀杆与活塞之间间隙初值的确定很重要。因为只有液体压力大于上碟簧弹力时,整个振动过程才可以启动。而初值的确定又与液体压力和弹力初值有关,因此需要选择并控制好上碟簧的起步压力。
由于振动组所受的弹力有一定预紧力,所以初期液体力增加,弹力不变。当超过预紧力后,弹力才随着位移增大而逐渐增大。
从图 12可以看到,当间隙减到最小后,2速度合为一条线,表示2运动部件在最小间隙下发生速度的碰撞,碰撞后一起向前运动,一直运动到阀杆上的弹力大于液体力或运动位移达到预设的最大行程(通过限位装置卡住,由于运动的合速度是液体流动的最大流速,速度比较小,故对限位装置的强度要求不高)时开始脱离振动组,间隙也被拉开;随着间隙增大,液体力迅速减小,2运动部件也开始反弹,振动组最终撞到振动下端,回程速度终止。
模拟计算的振动频率是19.72 Hz,满足振动频率要求。此状态下的冲量可以根据质量和速度增量计算:ΔP冲量=mΔv=10×7.2=72 (kg·m/s)。具体的冲击力只需除以冲击时间即可得到。如果冲击力不合适则通过调节下碟簧的特性来改善。
4 结论(1) 在连续管水平钻井中,管柱与井壁之间的摩阻是影响钻井深度的重要因素,而井下振动减摩工具可以很好地减轻管柱的摩阻,延伸管柱的入井位移。
(2) 以机械式振动减阻器为研究对象,用有限元软件设计了井下减摩振动器的具体结构。采用ANSYS Fluent模拟计算出振动过程中液体压力随阀口间隙的变化规律,据此关系计算并选出2个碟形弹簧的特性参数。
(3) 将相关参数植入用Simulink模块建立的振动仿真系统中,计算了整个振动过程中减阻器各参数随时间的变化规律。研究结果可以为类似振动减阻器的设计提供参考。
| [1] | 郭永峰, 白云程. 国内外钻井摩阻力研究的现状及趋势[J]. 国外油田工程, 2001, 17(8): 31–33. |
| [2] | 易先中, 宋顺平, 陈霖, 等. 复杂结构井中钻柱托压效应的研究进展[J]. 石油机械, 2013, 41(5): 100–104, 110. |
| [3] | MITCHELL R F. Comprehensive analysis of buckling with friction[J]. SPE Drilling & Completion, 1996, 11(3): 178–184. |
| [4] | MCCORMICK J E, CHIU T F. The practice and evolution of torque and drag reduction: Theory and field results[R]. SPE 147100, 2011. |
| [5] | WEATHERFORD. Mechanical friction reduction tools[EB/OL].[2017-04-12]. http://www.weatherford.com/Products/Drilling/Drilling tools Rentals/Torqueand Drag Reduction/2002-2013. |
| [6] | 付加胜, 李根生, 史怀忠, 等. 井下振动减摩技术研究进展[J]. 石油机械, 2012, 40(10): 6–10, 45. |
| [7] | 常玮, 易先中, 万继方, 等. 机械振动降摩减阻技术在滑动钻井中的应用[J]. 机械工程师, 2015(3): 146–148. |
| [8] | 张云飞, 贺会群, 都亚男, 等. 连续管井下减阻器研究进展[J]. 石油机械, 2015, 43(7): 36–41. |
| [9] | CONNELL M L, FERGUSON A M, LOVING S W, et al. Vibrating tool: US2010/0276204. Al[P]. 2010-11-04. |
| [10] | STOESZ C W. Downhole vibrator: US6474421. B1[P]. 2002-11-05. |
| [11] | ALLAHAR I, MERCADO J, GRIGOR C. Vibrating downhole tool: US7708088. B2[P]. 2010-05-04. |
| [12] | NEWMAN K, BURNETT T, PURSELL J, et al. Modeling the affect of a downhole vibrator[R]. SPE 121752, 2009. |
| [13] | WICKS N, PABON J, ZHENG A. Modeling and field trials of the effective tractoring force of axial vibration tools[R]. SPE 170327-MS, 2014. |
| [14] | 刘华洁, 高文金, 涂辉, 等. 一种能有效提高机械钻速的水力振荡器[J]. 石油机械, 2013, 41(7): 46–48. |
| [15] | ALALI A, BARTON S, MOHANNA A. Unique axial oscillation tool enhances performance of directional tools in reach applications[R]. SPE 143216, 2011. |
| [16] | SOLA K I. New downhole tool for coiled tubing extended reach[R]. SPE 60701, 2000. |
| [17] | 易灿, 李根生, 范红康. 井下振动减摩器的设计及试验研究[J]. 石油矿场机械, 2003, 32(6): 42–44. |
| [18] | 杨浩. 基于脉冲激励的水平井减摩降阻工具研制[D]. 成都: 西南石油大学, 2015. |
| [19] | 张鹰, 吴如凡. 基于流场分析的限流孔板设计[J]. 广州化工, 2015(23): 209–211. DOI: 10.3969/j.issn.1001-9677.2015.23.069 |
| [20] | 柳鹤. 射流式水力振荡器理论分析与试验研究[D]. 长春: 吉林大学, 2014. |




