2. 路易斯安那大学拉菲特分校
2. University of Louisiana at Lafayette
0 引言
随着钻井作业环境的日趋复杂,加之非常规、深水、深层和极地等油气田数量的增长,科学的精确井眼轨迹控制是确保各种复杂井钻井成功的关键,同时也是提高钻井成功率和效率,实现钻井井眼轨迹参数优选的核心技术。目前,在三维复杂井眼轨迹中主要采用遗传算法[1]和多目标遗传算法[2]实现控制转矩的优化,但这2种算法在运行效率及最优解2个方面都有待改善。为提高三维复杂井眼轨迹控制转矩的优化结果精度和优化速度,笔者针对三维复杂井眼轨迹优化问题中约束条件复杂、自变量多的特点,设计了一种新的粒子群算法(a new Particle Swarm Optimization, NPSO)。在各井段、套管长度及目标垂深等9个约束条件下[3-6],应用NPSO优化实际控制转矩(True Control torque, TCT),完成井身、井斜角、井斜方位角以及井段曲率等16个参数的优选,实现精确、高效的井眼轨迹控制。仿真结果表明:与MOGA和GA算法相比,NPSO优化TCT的结果更优,算法运行速度更快,耗时更短。将NPSO应用于实际钻井过程中井眼轨迹控制,既提高控制实时性和钻井效率,又节约了钻井成本,缩短了钻井时间。
1 NPSO概述粒子群算法由KENNEDY和EBERHART于1995年提出,起源于对鸟群捕食行为的研究过程[7]。与其他进化算法相似,粒子群算法通过种群中个体间的协作与竞争,实现在搜索空间内寻找最优解。粒子群算法的基本思想是模拟生物界的群体与环境和群体内个体之间的生物行为,利用群体中个体对信息的共享,使整个群体的运动在求解问题空间汇总产生从无序到有序的演化过程,从而获得最优解。粒子群算法具有并行性高、鲁棒性强、收敛快、规则简单和容易实现等优点。NPSO算法中主要算子有初始化、速度更新与约束、位置更新与约束等。
1.1 NPSO初始化正交初始化较复杂,在此采用简单的随机初始化策略。初始化的伪代码为:
for p=1:POP
for xd=1:VAR
Dvalue= Xmax(xd)-Xmin(xd)
x(p, xd)= -Dvalue +2*Dvalue *rand;
end
end
其中:Xmax和Xmin分别为待优化自变量的最大和最小值,解空间X由16维决策向量组成R16,POP为粒子种群的大小,POP=65,VAR为待优选的自变量的个数,VAR=16。
1.2 速度更新与约束当粒子速度较大时算法的全局搜索能力较强,当粒子速度变小时算法的局部搜索能力较强。为了使算法在进化的初期阶段尽可能地搜索到更加广阔的区域,而在进化的后期阶段提高算法的收敛性粒子,将惯性权重w采用线性递减策略(LDW)。
在约束优化中,粒子群算法的速度约束是指速度上限约束和当速度超出上限时的处理。考虑到惯性权重和算法收敛速度,将速度上限均设置为位置上、下限距离。由于算法中粒子更新和变异后其速度均会改变,所以在此之后进行速度约束处理以减少无用计算。速度更新与约束的伪代码为:
for p = 1 to POP
c1=0.269 9;c2=4.237 3;wmax=0.9;wmin=0.4;
wwid=wmax-wmin;
w=wmax-wwid*ite/ITE;
r1=rand; r2=rand; varyr=rand; varys=randsrc;
v(p)=w*v(p)+c1*r1*(xp(p)-x(p))+c2*r2*(xg(p)-x(p));
end for
其中:c1和c2分别为认知学习因子和社会学习因子;ite为当前进化次数,ITE为最大进化次数,ITE=100;wmax为w的最大值,wmin为w的最小值;在p时刻每个粒子所经过的最佳位置为xp(p),群体所发现的最佳位置为xg(p)。
为了增强粒子跳出局部最优的能力,通过变异操作对速度施加扰动以避免早熟。但变异算子也可能损坏已搜索到的最优结果,因此变异概率应随迭代次数增加而下降。变异算法的伪代码为:
varyp = 1 -ite/ITE;
for p = 1 to POP
varyr = rand; varys = randsrc;
if(varyr < varyp)
v(p)=3*varys*(1-varyr)*v(p);
end if
end for
速度约束处理的伪代码为:
for xd = 1:VAR
if v(p, xd)>vmax(xd)
v(p, xd)=vmax(xd);
elseif v(p, xd) < -vmax (xd)
v(p, xd) = -vmax (xd);
end if
end for
其中:vmax为粒子速度的最大值,vmin为粒子速度的最小值。
1.3 位置更新与约束粒子的位置更新和变异后,其有可能超出定义的边界范围,使得到的最优值不在定义域范围内,不满足问题的约束条件。位置约束处理是把超出边界的粒子位置设定在边界上,并将其速度减半,方向反向。位置约束处理的伪代码为:
for p = 1:POP
for xd = 1:VAR
if x(p, xd)>xmax(xd)
x(p, xd)=xmax(xd);
v(p, xd)= -0.5 * v(p, xd);
elseif x(p, xd) < xmin(xd)
x(p, xd)=xmin(xd);
v(p, xd)=-0.5* v(p, xd);
end if
end for
其中:xmax为粒子位置的最大值,xmin为粒子位置的最小值。
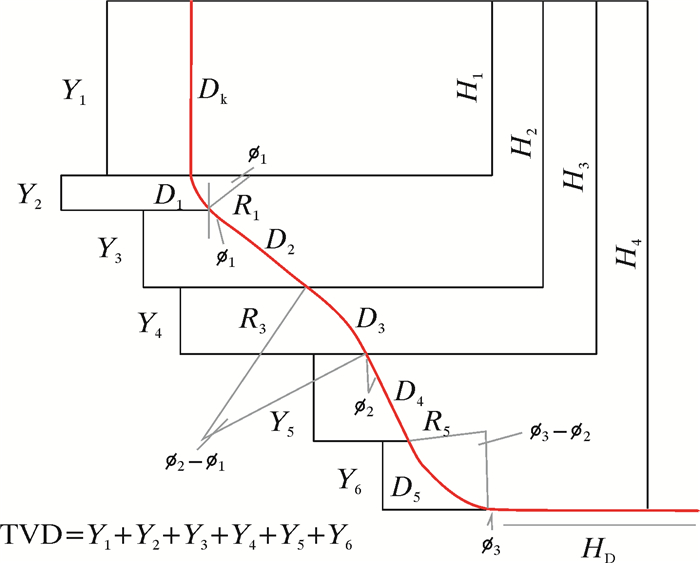
2 三维复杂井眼控制转矩优化 2.1 复杂井眼各段转矩的计算复杂井眼轨迹的垂直横截面如图 1所示。
|
| 图 1 复杂井眼轨迹的垂直横截面 Fig.1 Vertical cross-section of the complex well trajectory |
图 1中:H1为造斜点深度;H2为第1段造斜稳斜结束深度;H3为降斜段结束深度;H4为总垂直深度;D1为第1段增斜段;D2为正切段;D3为降斜段;D4为稳斜段;D5为第2段增斜段;HD为水平段井身长度。各段计算公式定义为[9]:

|
(1) |
其中
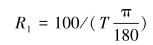
|
(2) |
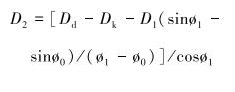
|
(3) |
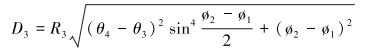
|
(4) |
其中
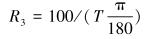
|
(5) |
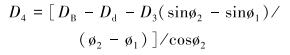
|
(6) |
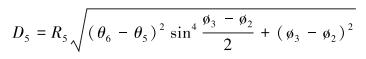
|
(7) |
其中
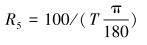
|
(8) |
式中:Φ1、Φ2、Φ3分别为第1、第2、第3段的稳斜角,θ1为造斜点的方位角;θ2为第1段靶点的方位角;θ3为第1段稳斜段的方位角;θ4为第2段造斜或降斜段的方位角;θ5为第2段稳斜段的方位角;θ6为第2段增斜段的方位角。
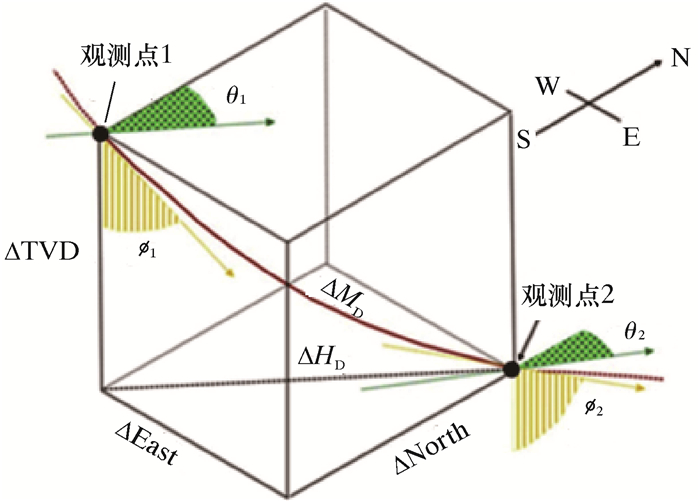
增斜段井眼的三维示意图如图 2所示。
|
| 图 2 增斜段井眼的三维示意图 Fig.2 Three-dimensional schematic diagram of the buildup section well trajectory |
图 2中曲线ΔMD的长度计算公式如下:

|
(9) |
其中,曲率半径r的计算式为:
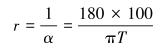
|
(10) |
ΔMD在垂直方向上的增量为:

|
(11) |
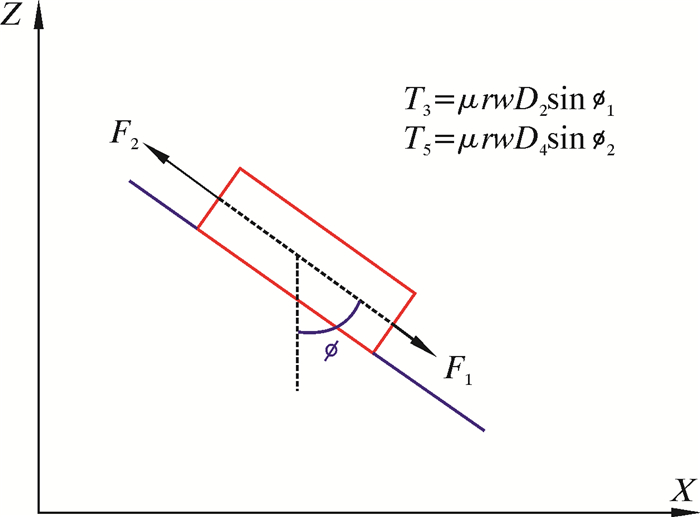
|
| 图 3 D2、D4稳斜段对应的转矩T3、T5示意图 Fig.3 The torque T3 and T5 corresponding to tangent section of D2 and D4 |
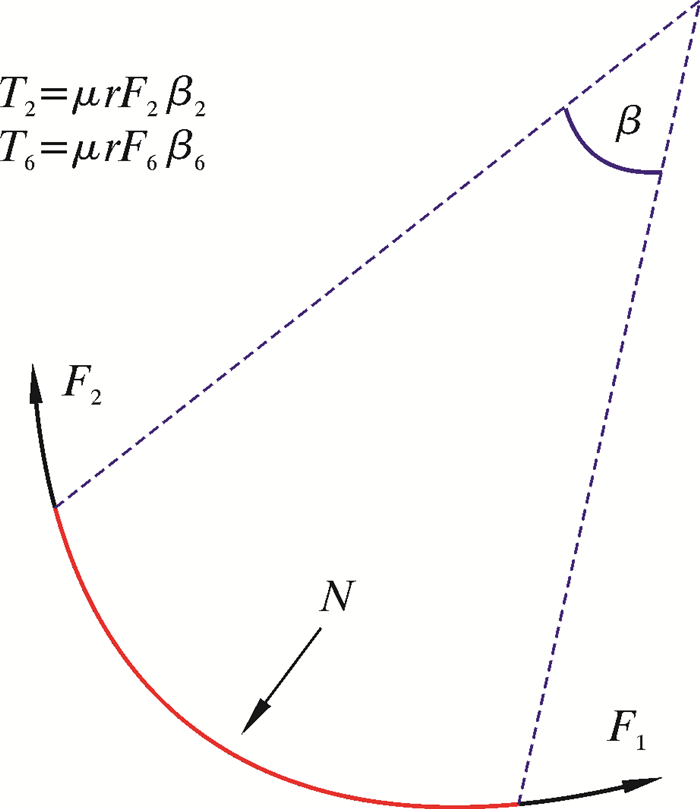
|
| 图 4 D1和D5增斜段对应的转矩T2、T6示意图 Fig.4 The torque T2 and T6 corresponding to tangent section of D1 and D5 |
|
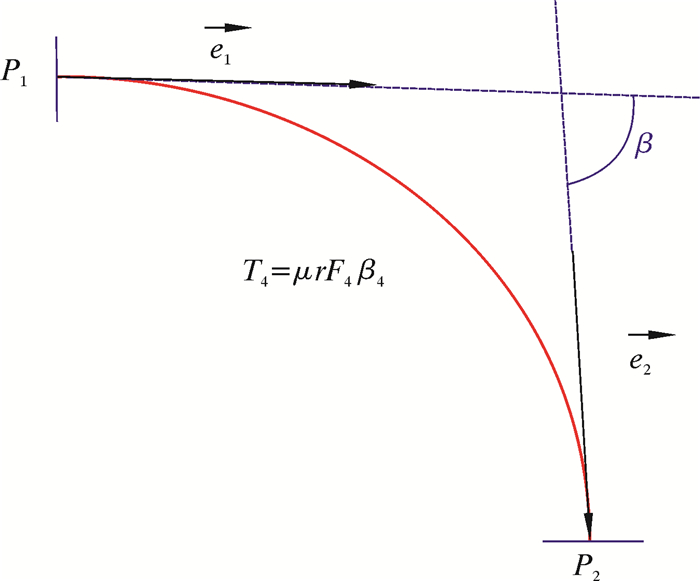
| 图 5 D3降斜段对应的转矩T4示意图 Fig.5 The torque T4 corresponding to drop-off section of D3 |
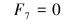
|
(12) |
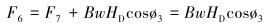
|
(13) |
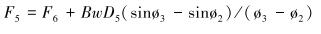
|
(14) |
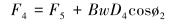
|
(15) |
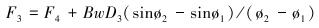
|
(16) |
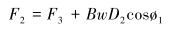
|
(17) |
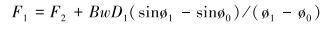
|
(18) |
根据图 3~图 5和式(12)~式(18) 计算F1~F7对应的转矩T1~T7,计算式如下:
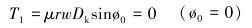
|
(19) |
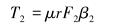
|
(20) |
其中
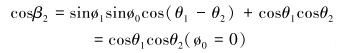
|
(21) |
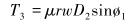
|
(22) |
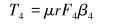
|
(23) |
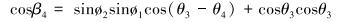
|
(24) |
其中
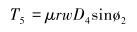
|
(25) |
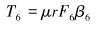
|
(26) |
其中
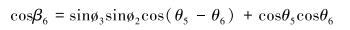
|
(27) |

|
(28) |
图中及式中各符号含义如下:Dk为造斜点深度;DB为第1段降斜段起点的实际垂直深度;P1、P2为2个观测点;e1、e2为井筒方向上的单位向量;F1为定向井底部的轴向力;F2为定向井顶部的轴向力;β为总的角度变化;B为浮力系数;B=0.7;μ为摩擦因数,μ=0.2;w为单位钻具重力,w=10 kN/m;r为钻杆半径,r=30 mm。
通过式(10)~式(28) 计算出各井段的受力及相应的转矩T1~T7,在复杂井眼轨迹控制转矩优化中,实际控制转矩等于各井段转矩之和。
2.2 待优化目标函数定义针对复杂井眼轨迹控制转矩优化问题,以复杂井眼轨迹为研究对象,以自变量的取值、各井段、套管长度及目标垂直井深为约束条件,采用NPSO优化复杂井眼实际控制转矩TCT,完成井身、井斜角、井斜方位角及井段曲率等16个参数的优选,待优化目标函数TCT定义为:

|
(29) |
式中:min{TCT}为待优化目标函数;解空间X由16维决策向量组成R16,即X=(HD, Φ1~Φ3, θ1~θ6, Dd, DB, Ds1~Ds3, Dk)∈R16;s.t.为待优化问题的约束条件;j为套管设计段数;Hvmin、Hvmax分别为井眼轨迹的垂深下限和上限。自变量的约束边界及约束条件如表 1所示。
| 变量 | 约束边界 | |
| 下限 | 上限 | |
| Hv/m | 3 293 | 3 322 |
| HD/m | 762 | 762 |
| Ds1/(°) | 0 | 5 |
| Ds2/(°) | 0 | 5 |
| Ds3/(°) | 0 | 5 |
| Φ1/(°) | 10 | 20 |
| Φ2/(°) | 40 | 70 |
| Φ3/(°) | 90 | 95 |
| θ1/(°) | 270 | 280 |
| θ2/(°) | 270 | 280 |
| θ3/(°) | 270 | 280 |
| θ4/(°) | 330 | 340 |
| θ5/(°) | 330 | 340 |
| θ6/(°) | 355 | 360 |
| Dk/m | 183 | 305 |
| Dd/m | 1 830 | 2 134 |
| DB/m | 3 048 | 3 109 |
| C1/m | 549 | 671 |
| C2/m | 2 195 | 2 652 |
| C3/m | 3 139 | 3 353 |
| 注:C1为到达第1造斜点的套管垂深;C2为到达第2造斜点的套管垂深;C3为到达第3造斜点的套管垂深。 | ||
3 仿真结果及分析 3.1 仿真结果
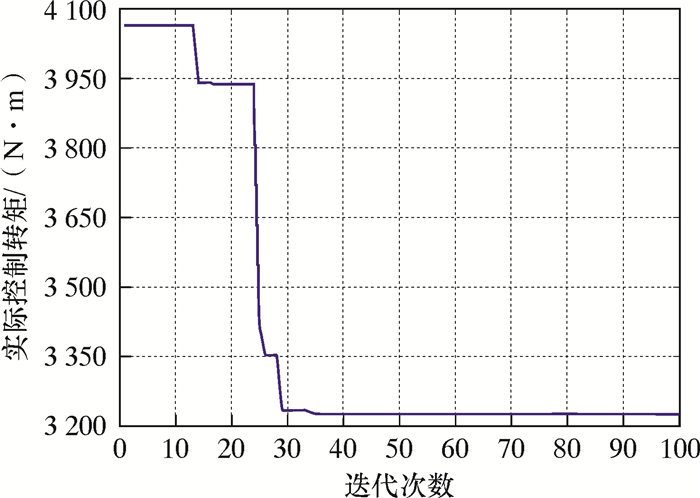
采用NPSO优化三维井眼轨迹中TCT的仿真结果如图 6所示。
|
| 图 6 NPSO优化TCT的仿真结果 Fig.6 Simulation results of TCT optimized by NPSO |
图 6中,采用NPSO实现三维复杂井眼实际控制转矩TCT优化,横坐标为迭代次数,ITE=100,纵坐标为每代获得最优实际控制转矩。
3.2 优化结果比较以实际控制转矩TCT为优化目标,以自变量的取值,各井段、套管长度及目标垂直井深为约束条件,实现16维决策向量X∈R16的优选,将优化结果与其他智能算法(MOGA和GA算法)优化TCT的结果进行比较,如表 2所示。表中T为转矩,t为运行时间。
| 算法 | NPSO | MOGA | GA |
| T/(N·m) | 3 225 | 3 587 | 3 741 |
| Hv/m | 3 320 | 3 308 | 3 307 |
| t/s | 10.133 | - | 526.000 |
| Φ1/(°) | 10.0 | 10.0 | 10.0 |
| Φ2/(°) | 40.0 | 40.0 | 40.0 |
| Φ3/(°) | 93.0 | 92.0 | 90.0 |
| θ1/(°) | 277.0 | 270.0 | 270.0 |
| θ2/(°) | 270.0 | 280.0 | 280.1 |
| θ3/(°) | 280.0 | 280.0 | 276.0 |
| θ4/(°) | 330.0 | 331.0 | 340.0 |
| θ5/(°) | 340.0 | 331.0 | 340.0 |
| θ6/(°) | 355.0 | 357.0 | 356.0 |
| Dd/m | 2 134 | 2 133 | 2 134 |
| Db/m | 3 109 | 3 109 | 3 109 |
| Dk/m | 231 | 305 | 305 |
| HD/m | 762 | 762 | 762 |
| ITE | 100 | 610 | 152 |
由表 2可知,与MOGA和GA算法优化结果相比[1],NPSO算法的最优解更优且算法收敛速度更快,运行效率提高,运行时间明显缩短。因此,将该方法用于实际钻井过程,将提高优化过程实时性和钻井效率,节约钻井成本。
3.3 算法的复杂度分析为了进一步分析NPSO算法的有效性,比较NPSO、MOGA和GA算法的时间复杂度和空间复杂度,结果如表 3所示。
| 算法 | 时间复杂度T(n) | 空间复杂度S(n) |
| NPSO | O(n2) | O(n2) |
| MOGA | O(cn) | O(n3) |
| GA | O(n2) | O(n3) |
由表 3可知,当种群规模为n时,与MOGA和GA算法相比,NPSO降低了算法的时间复杂度,提高了算法的效率,缩短了运行时间。
4 结束语针对复杂井眼轨迹优化问题中自变量多,约束条件复杂的特点,笔者设计了一种新的粒子群算法以提高复杂井眼轨迹控制精度和优化速度。在各井段、套管的长度及目标垂直井深等9个约束条件下,应用NPSO优化实际控制转矩,完成井身、井斜角、井斜方位角以及井段曲率等16个参数的优选,实现精确、高效的井眼轨迹优化。试验结果表明:与MOGA和GA算法相比,NPSO优化TCT的结果更优,算法的运行速度更快。将NPSO应用于实际钻井过程中井眼轨迹控制,可以提高钻井效率,节约钻井成本,缩短钻井时间。
| [1] | ADAMS J N, CHARRIER T. Drilling engineering: A complete well planning approach[M]. Tulsa, Oklahoma: PennWell Publishing Company, 1985: 342-345. |
| [2] | MANSOURI V, KHOSRAVANIAN R, WOOD D A, et al. 3-D well path design using a multi-objective ITEetic algorithm[J]. Journal of Natural Gas Science & Engineering, 2015, 27(1): 219–235. |
| [3] | ATASHNEZHAD A, WOOD D A, FEREIDOUNPOUR A, et al. Designing and optimizing deviated wellbore trajectories using novel particle swarm algorithms[J]. Journal of Natural Gas Science & Engineering, 2014, 21: 1184–1204. |
| [4] | WOOD D A. Hybrid cuckoo search optimization algorithms applied to complex wellbore trajectories aided by dynamic, chaos-enhanced, fat-tailed distribution sampling and metaheuristic profiling[J]. Journal of Natural Gas Science & Engineering, 2016, 34: 216–252. |
| [5] | WOOD D A. Hybrid bat flight optimization algorithm applied to complex wellbore trajectories highlights the relative contributions of metaheuristic components[J]. Journal of Natural Gas Science & Engineering, 2016, 32: 211–221. |
| [6] | SHOKIR E M, EMERA M K, EID S M, et al. A new optimization model for 3D well design[J]. Oil & Gas Science and Technology, 2004, 59(3): 255–266. |
| [7] | 王静. 多目标粒子群优化算法的研究及应用[D]. 大庆: 东北石油大学, 2011. |



