0 引言
目前,我国约有60%的油气管道服务年限超过20 a[1]。很多埋地管道和海底管道运行多年,最外层的防腐层已经完全腐蚀,外表面容易出现局部腐蚀情况,严重影响着管道的安全运行。因此,研究管道修复技术具有重要的现实意义。管道修复技术主要有焊接修复、夹具修复以及复合材料修复[2]。相比于其他修复技术,复合材料修复技术具有修复时间短、修复工艺简单以及修复成本低的优势[3],已被现场证明是一种可靠的修复方式[4]。
国内外学者针对复合材料修复技术做了大量研究。J.M.DUELL等[4]运用半解析法和数值法研究了不同尺寸缺陷管道的复合材料修复情况。A.SHOUMAN[5]通过试验研究了组合载荷工况下复合材料修复管道的拉压极限。王勇军等[6]利用有限元模拟了缠绕层厚度与缺陷面积和深度的关系。以上研究都没有考虑复合材料层与管道之间的界面应力以及修复后管道的失效模式,这在一定程度上影响着了结果的准确性。为此,笔者提出了一种符合实际情况的复合材料缠绕修复腐蚀管道有限元模型,并对模型的准确性进行了试验研究,所得结论可为进一步研究复合材料修复技术提供数据支撑。
1 复合材料有限元模型研究 1.1 连接层的Cohesive单元Cohesive单元是ABAQUS软件中的一种粘结单元,主要用于分析复合材料界面及不同试件胶接连接等界面问题。Cohesive单元既可分析二维问题,也可以分析三维问题。
1.2 Cohesive单元失效准则复合材料层与管道之间的连接界面采用Cohesive单元。由于环氧树脂是各向同性,界面上只有轴向的正应力和其他2个平面的剪应力。Cohesive单元本构方程如下:
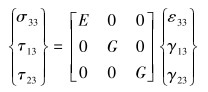
|
(1) |
式中:ε33为连接层厚度方向上的主应变;γ13和γ23为连接层垂直于厚度方向上的2个剪切应变,G和E分别为材料的弹性模量及剪切模量。
目前只有很少的模型在预测失效起点时考虑到牵引部分的相互作用。笔者基于Ye准则[7], 考虑牵引部分的相互作用,运用牵引力二次方的相互关系进行研究,即:

|
(2) |
式中:f开始是界面失效函数,Xt是界面拉伸强度,St是界面剪切强度。
损伤扩展准则通常与损伤发生准则相互独立。脱粘扩展的失效准则可以表示为:
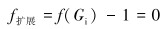
|
(3) |
式中:f扩展是纯模式破裂能,f(Gi)是主方向的能量释放率。
Cohesive单元失效准则就是通过脱粘失效起点准则和脱粘扩展失效准则共同作用,并利用ABAQUS自带的Quads准则和Exponential damage evolution准则来定义脱粘失效起点和脱粘扩展失效。当Quads准则中QUADSCRT场变量大于等于1时,粘接层开始发生失效。
1.3 Hashin准则复合材料强度准则采用的是模式相关三维Hashin准则[8],它不仅给出了失效条件,也给出了材料失效模式,可以更加清楚地了解复合材料修复管道结构的失效过程。三维Hashin准则如下。
纤维拉伸失效(σ11 > 0):
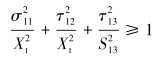
|
(4) |
纤维压缩失效(σ11 < 0):

|
(5) |
基体拉伸失效(σ22 > 0):

|
(6) |
基体压缩失效(σ22 < 0):

|
(7) |
式中:σ11、σ22、τ12、τ13和τ23为复合材料单层板的2个正应力和3个剪切应力,Xt、Xc、Yt、Yc、S12、S13和S23为复合材料单层板的7个强度参数。
由于ABAQUS软件中的Hashin准则只能作用于Shell单元,而文中复合材料选用的是Solid单元,所以通过ABAQUS子程序USDFLD将三维Hashin准则写入到ABAQUS中,并采用Camanho[9]参数退化方式, 具体如表 1所示。复合材料失效模式通过ABAQUS中场变量来判断,FV1表示基体拉伸失效,FV2表示基体压缩失效,FV3表示纤维拉伸失效,FV4表示纤维压缩失效。当场变量达到1时,就认为发生了该种模式失效。
| 失效模式 | 参数退化 |
| 基体拉伸失效 | E22=0.22E22, G12=0.2G12, G23=0.2G23 |
| 基体压缩失效 | E22=0.4E22, G12=0.4G12, G23=0.4G23 |
| 纤维拉伸失效 | E11=0.07E11 |
| 纤维压缩失效 | E11=0.07E11 |
2 有限元模型建立 2.1 参数选取
根据试验条件选取外径25.00 mm,厚度2.50 mm,长度为300.00 mm的X60钢管, 模拟的缺陷通过机器加工成长度为20.00 mm,宽度为10.00 mm,深度为1.25 mm的矩形凹槽。玻璃纤维修复后的腐蚀管道见图 1。

|
| 图 1 修复后试验管道 Fig.1 The repaired test pipe |
根据ASMEPCC-2压力设备和管道规范中管道的非金属复合材料修复系统的要求[10],复合材料修复层最小厚度可以通过式(8) 计算。

|
(8) |
式中:D是管道外径,σ是管道最小屈服强度,Es和Ec分别是管道和复合材料层轴向拉伸模量,F是管道允许的最大拉伸载荷,ps是腐蚀管道允许的最大内压。
根据ASMEPCC-2规范,复合材料修复层最小长度由管道腐蚀长度、复合材料覆盖长度以及粘结剂堆叠长度决定,计算公式为[9]:
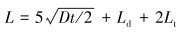
|
(9) |
式中:L是修复层的总长度,t是管道壁厚,Ld是缺陷部位长度,Lt是粘结剂堆叠长度。
这些参数也可以根据类似的规范所确定,包括ISO/TS-管道的复合材料修复和DNV-RP-F11-海底管道修复[11]。复合材料缠绕修复管道试验的材料参数[4]如表 2所示。
| 材料 | 弹性模量/GPa | 泊松比 |
| X60 | 210.0 | 0.30 |
| 修复剂 | 5.5 | 0.43 |
| 环氧树脂 | 3.6 | 0.40 |
| 玻璃纤维 | 85.0 | 0.20 |
2.2 有限元模型建立形式选取
为了节约计算时间,同时保证结构的完整性,取½管道模型进行研究。边界条件为关于Z轴对称。为了研究管道与复合材料层间的应力,在模型中引入Cohesive单元,用来模拟界面[12]。Cohesive单元节点的连接方式有2种,如图 2所示。若通过共节点方式进行粘接,单元厚度为0,采用独立网格结构建模。若通过tie约束进行连接,Cohesive单元厚度设定成一个很小的值。

|
| 图 2 Cohesive单元节点连接方式 Fig.2 Node connection of the Cohesive unit |
3 复合材料缠绕修复腐蚀管道试验与有限元分析 3.1 复合材料修复试验研究
针对复合材料缠绕修复腐蚀管道分别进行了3组试验, 试验地点在中国石油大学(北京)工程西楼。第1组和第2组试验分别是完好管道和未修复腐蚀管道的拉伸试验。第3组是玻璃纤维布缠绕腐蚀管道的拉伸试验,其中复合材料修复管道模型包括钢管、环氧修复剂和玻璃纤维布修复层。钢管是API 5LS等级的X60钢。修复剂用于填充管道腐蚀部位。环氧树脂用于玻璃纤维布和管道以及玻璃纤维布层与层之间的粘接。修复剂和粘接剂的固化在室温下需要24 h[4]。
管道通过拉伸试验机提供拉伸载荷,利用应变仪观察数据,拉伸载荷从10 kN逐次加到管道断裂,每次载荷增量为10 kN。每组拉伸试验做3次,取平均值。
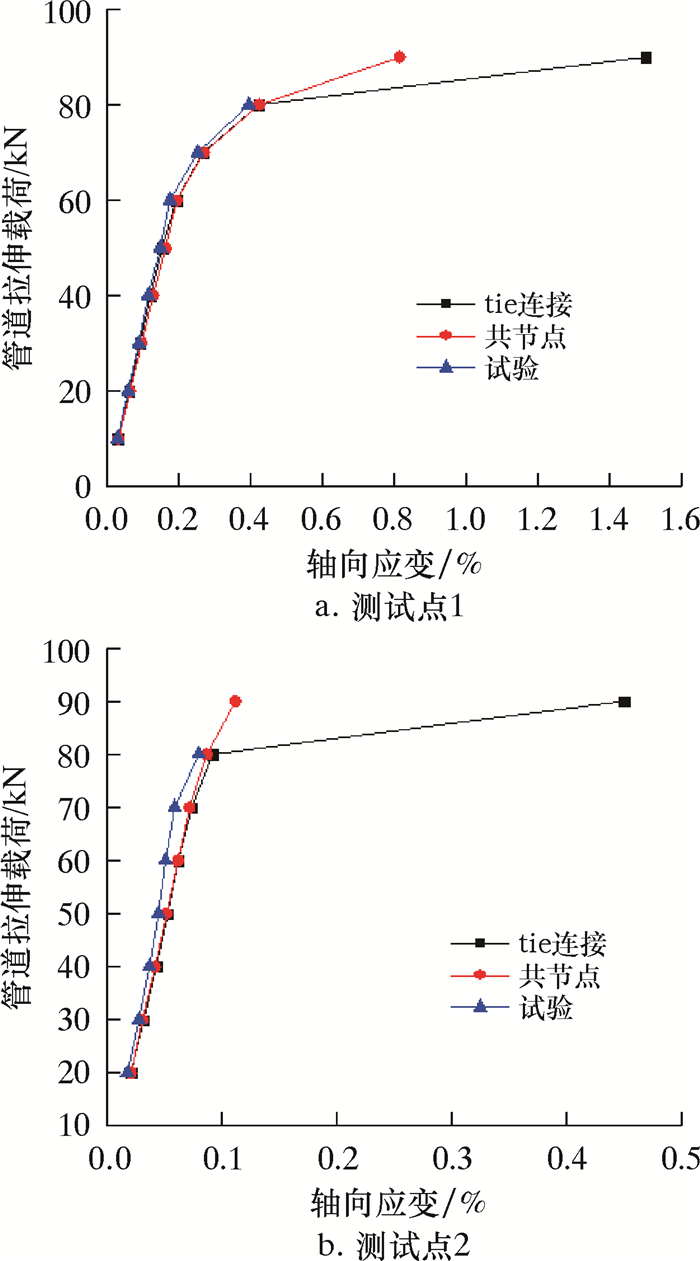
3.2 数值结果与试验结果比较 3.2.1 纤维与粘接剂界面的处理对结果的影响图 3为不同测试点处管道的拉伸载荷与应变曲线。
|
| 图 3 不同测试点处管道的拉伸载荷与应变曲线 Fig.3 Tensile load and strain curves of pipe at different test points |
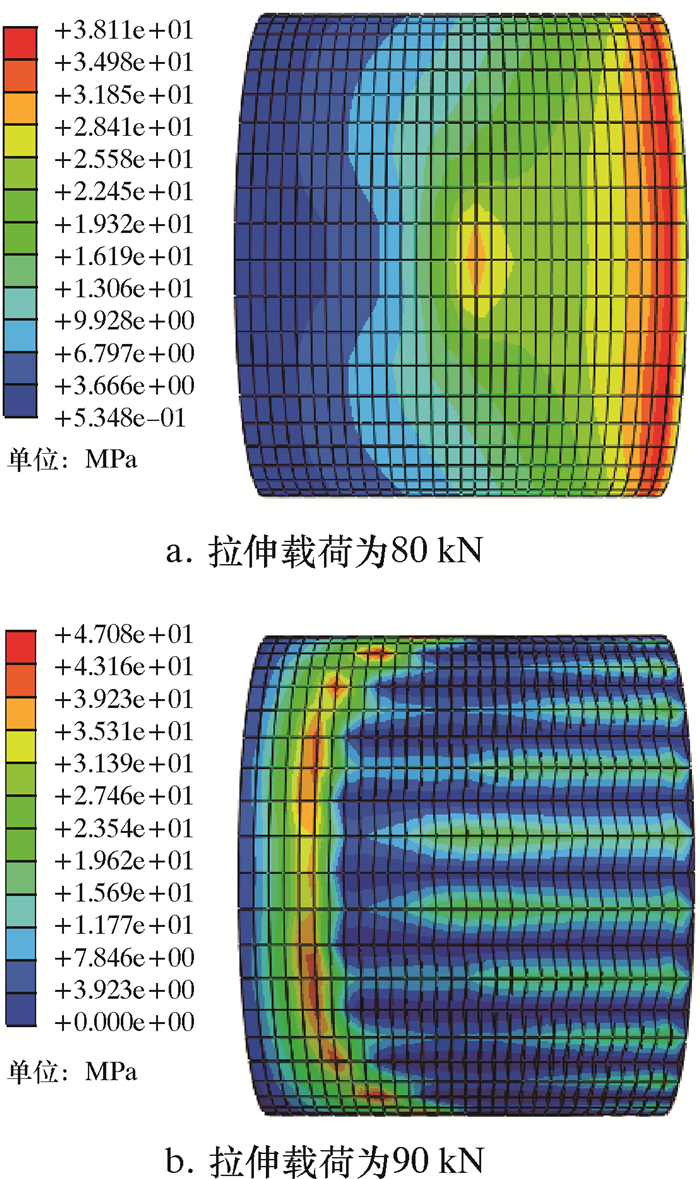
图 3a表明,当拉伸载荷小于80 kN时,随着拉伸载荷的增大,测试点的应变也逐渐变大,且共节点和tie约束连接结果非常接近,试验数据与数值计算数据略有偏差,但是拉伸载荷的应变曲线变化趋势都相同。当载荷达到80 kN时,3种结果的差距越来越大。试验中由于拉伸载荷未达到90 kN时管道已经拉断,所以当载荷达到90 kN时没有结果。当载荷达到90 kN时,相比于共节点界面处理的计算结果,tie约束连接的应变值急剧增大,这是因为共节点连接方式不能很好地模拟脱粘失效。图 4为tie约束时Cohesive单元应力云图。由图可知,当拉伸载荷为80 kN时,tie连接粘接层两端应力最大;当拉伸载荷为90 kN时,粘接层最大应力逐渐向粘接层中间转移,这能很好地模拟粘接层脱粘现象。因此,相比于共节点连接方式, tie约束模型能更准确地模拟复合材料修复管道脱粘现象。
|
| 图 4 tie约束时Cohesive单元应力云图 Fig.4 Stress distribution of the Cohesive unit under tie constraints |
3.2.2 建模方法对结果的影响
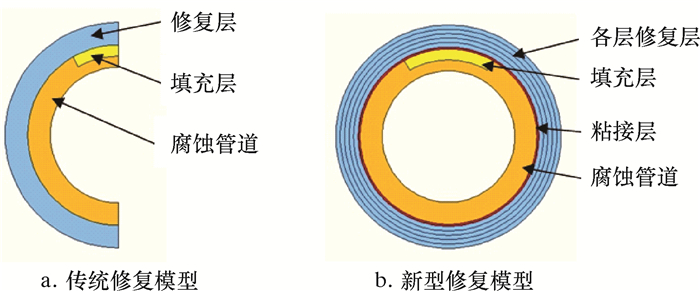
为了研究复合材料修复腐蚀管道模型的准确性,分别建立传统管道修复有限元模型和新模型,并将计算结果与试验结果做对比。传统模型采用¼管道模型,复合材料层材料参数按整体来计算[13]。由于传统模型中对称面存在应力集中问题,新模型采用½管道模型,复合材料层划分成许多纤维单层,铺设角按照0°/90°铺设,材料属性参照表 2中的数据,玻璃纤维布层与层之间使用Cohesive粘接单元。2种模型的截面如图 5所示。
|
| 图 5 不同修复模型截面图 Fig.5 Cross-sectional view of different repair models |
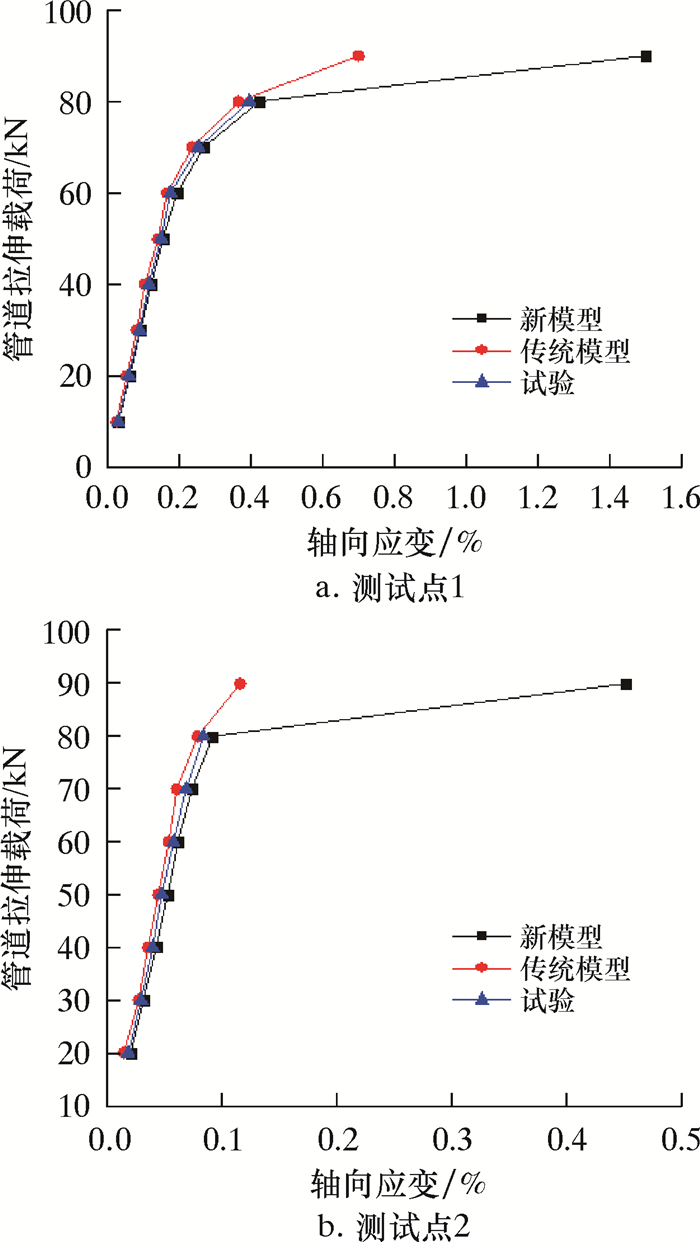
图 6为不同模型时测试点1和测试点2处管道拉伸载荷与应变曲线。由图可知,当拉伸载荷小于80 kN时,测试点1处2种模型和试验数据比较接近,且新模型计算出的应变最大,传统模型计算出的应变最小,这是传统模型的应力集中现象导致; 当拉伸载荷大于80 kN时,随着拉伸载荷增大,试验管道的应变已经消失,这是因为试验管道已经被拉断;新模型的管道应变变化加快,传统模型的应变变化相对缓慢,这是新模型模拟出了复合材料层的脱粘现象,当界面发生脱粘后,复合材料层修复效果明显降低,因此管道的应变急剧增大。图 6b中的变化规律与图 6a基本一致。因此,相比于传统模型,新模型计算出的结果更符合实际情况。
|
| 图 6 不同模型时管道的拉伸载荷与应变曲线 Fig.6 Tensile load and strain curves of pipe in different models |
3.3 失效模式研究
笔者以胜利油田铺设的海底管道为研究对象,管材型号为API X60,弹性模量为205 GPa[14],泊松比0.13,屈服强度413 MPa。运用上述方法建立新的碳纤维修复腐蚀海底管道有限元模型。管径324 mm,壁厚10 mm,管道长度2 m,管材为X60钢。其中腐蚀部位无量纲长度取6,无量纲宽度取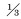

|
| 图 7 复合材料修复腐蚀海底管道模型 Fig.7 Model of repairing corroded submarine pipeline by composite material |
图 8为不同内压下腐蚀管道、完好管道和修复管道最大Mises应力图。由图可知,管道未屈服前,复合材料修复后管道最大Mises应力相比腐蚀管道减小了很多,修复效果明显,但是和完好管道相比还有很大差距。随着管道的屈服,复合材料修复后管道的最大应力与完好管道的差距逐渐缩小。

|
| 图 8 不同内压下3种管道最大Mises应力曲线 Fig.8 The maximum Mises stress curves of the three pipes under different internal pressures |
图 9为不同内压力下复合材料修复管道各层最大Mises应力曲线。由图可知,与复合材料层相比,粘接层上应力很小,即腐蚀管道受内压载荷时,粘接层不承受太大的载荷,主要起载荷传递作用。随着内压增大,复合材料层最大Mises应力增长速度越来越快,尤其是当管道屈服后,复合材料层承受的载荷更大,导致修复后管道的最大Mises应力与完好管道的差距逐渐缩小。因此,当管道达到屈服状态后,复合材料层修复的效果更加明显。
|
| 图 9 不同内压下复合材料修复管道各层最大Mises应力曲线 Fig.9 The maximum Mises stress curves of each layer of composite material repaired pipeline under different internal pressures |
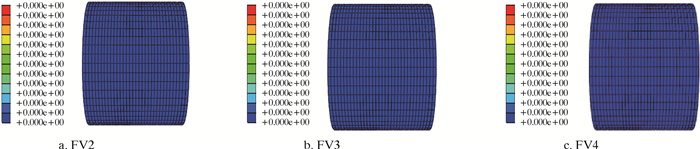
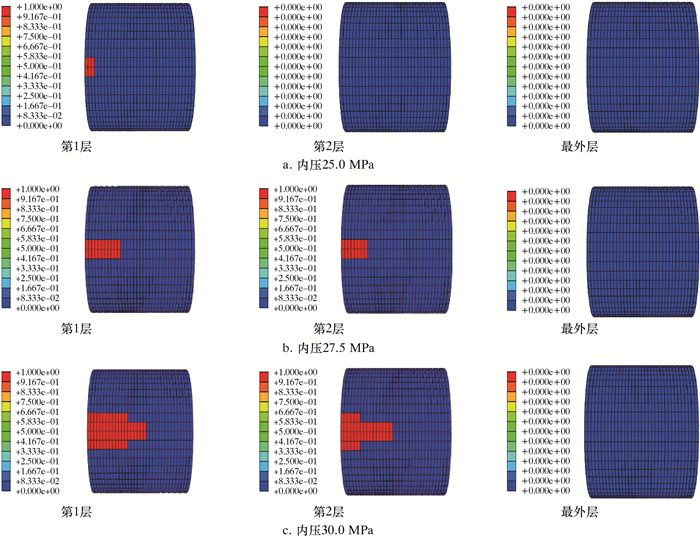
为了研究内压作用下复合材料修复腐蚀管道的失效模式,通过有限元模型计算修复结构各部分的失效状态。如图 10所示,修复管道内压达到30.0 MPa时,管道发生爆破,内压达到25.0 MPa时,FV1的场变量为1,复合材料层基体发生拉伸失效。内压小于30.0 MPa时,有限元结果中FV2、FV3和FV4的场变量都为0,说明在内压作用下管道在爆破前复合材料层不发生基体压缩、纤维断裂和纤维压缩失效。为了更加清楚地了解基体拉伸破坏的位置和失效扩展的规律,分别列出内压为25.0、27.5和30.0 MPa时的第1层、第2层和最外层的复合材料失效图,如图 11所示。
|
| 图 10 内压25.0 MPa时复合材料修复层第1层失效状态(场变量) Fig.10 The failure state of the first layer of composite material repaired layers under the internal pressure of 25.0 MPa (field variable) |
|
| 图 11 不同内压时复合材料修复层各层拉伸失效状态(场变量) Fig.11 The tensile failure state of composite material repaired layers under different internal pressures (field variable) |
由图 11b可知,复合材料层第1层和第2层都发生基体拉伸失效,并且失效的面积越来越小,因此认为复合材料层的失效由内向外扩展。由图 11c可知,当管道发生爆破,复合材料层最外层还没有发生纤维拉伸破坏,因此认为此时复合材料还未全部发生失效。
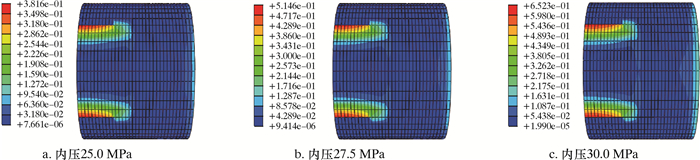
为了研究内压作用下复合材料修复管道是否发生脱粘现象,给出了不同内压作用下粘结层失效起点判据图(见图 12),由于失效起点的场变量都小于1,所以复合材料修复管道在内压作用下不发生脱接现象。
|
| 图 12 不同内压作用下粘接层失效状态(场变量) Fig.12 The failure state of bonding layer under different internal pressures (field variable) |
综上,当腐蚀海底管道经过碳纤维布复合材料修复后,随着内压的增大,失效的模式为基体拉伸失效,不发生粘接层脱粘和纤维断裂,而且当管道发生爆破,复合材料层还未完全发生失效。因此,复合材料修复腐蚀海底管道的极限内压就是修复后管道爆破时的内压。有限元计算得出复合材料修复管道的极限内压为29.0 MPa。
4 结论(1) 在复合材料缠绕腐蚀管道模型中,腐蚀管线与复合材料之间使用Cohesive粘接单元,粘接层与复合材料以及粘接层与管道的界面采用tie约束时,有限元分析结果与实际更加接近, 并且能够模拟出界面脱粘失效的现象。因此,在研究复合材料缠绕修复腐蚀管道时,有限元模型界面应采用Cohesive单元,连接方式应采用tie约束连接。
(2) 与传统复合材料修复模型相比,新型复合材料修复模型计算结果与试验结果更加接近。同时能够模拟出粘接层的脱粘现象以及复合材料层基体开裂和纤维拉伸失效现象,这为复合材料缠绕修复管道的后续研究提供了可靠的数值支撑。
(3) 复合材料层使用hashin准则判断失效时,可以更清楚地了解管道的失效模式。当管道受拉伸时,粘接层会先发生脱粘现象;当管道在内压载荷作用时,复合材料层最内层基体首先开裂,然后再向外层逐渐扩散, 并且管道爆破时,复合材料层未发生完全失效。
| [1] | 中国石油管道公司. 油气管道检测与修复技术[M]. 北京: 石油工业出版社, 2010. |
| [2] | 宋文, 刘艳东, 刘刚. 国内外管道修复技术的发展及应用[J]. 中国高新技术企业, 2009(18): 129. DOI: 10.3969/j.issn.1009-2374.2009.18.071 |
| [3] | ALEXANDER C, FRANCINI B. State of the art assessment of composite systems used to repair transmission pipelines[R]. IPC 2006-10484, 2006. |
| [4] | DUELL J M, WILSON J M, KESSLER M R. Analysis of a carbon composite overwrap pipeline repair system[J]. International Journal of Pressure Vessels & Pining, 2008, 85(11): 782–788. |
| [5] | SHOUMAN A, FARID T. Compressive strain limits of composite repair pipelines under combined loading states[J]. Composite Structures, 2011, 93(5): 1538–1548. |
| [6] | 王勇军, 王鹏, 王峰会, 等. 含缺陷高压管道复合材料补强有限元模拟[J]. 压力容器, 2007(10): 13. DOI: 10.3969/j.issn.1001-4837.2007.10.004 |
| [7] | LIN Y. Role of matrix resin in delamination onset and growth in composite laminates[J]. Composites Science and Technology, 1988, 33(4): 257–277. DOI: 10.1016/0266-3538(88)90043-7 |
| [8] | 刘勇, 陈世健, 高鑫, 等. 基于Hashin准则的单层板渐进失效分析[J]. 装备环境工程, 2010, 7(1): 34–37. |
| [9] | CAMANHO P P, MATTHEWS F L. A progressive damage model for mechanically fastened joints in composite laminates[J]. Journal of Composite Materials, 1999, 33(24): 2248–2280. DOI: 10.1177/002199839903302402 |
| [10] | ANON. Repair of pressure equipment and piping:ASME PCC-2[S]. Washington DC:ASME, 2008. |
| [11] | ANON. Pipeline subsea repair:DNV-recommended practice-F113[S]. Olso:Norske Veritas, 2007. |
| [12] | ZHOU Y W, CHEN X L, FAN Z H, et al. Bond behaviors of FRP-to-concrete interface under the control of a novel end-anchorage system[J]. Composite Structures, 2017, 168(5): 130–142. |
| [13] | RAMADAN S, BONIN A M, KENNEDY B J, et al. Stress analysis of fiber-reinforced composite materials[J]. WCB Mcgraw-Hill, 1998, 18(2): 123–128. |
| [14] | 张小勇. 腐蚀海底管道极限承载力和失效机理研究[D]. 杭州: 浙江大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013147667.htm |



