2. 中国石油大学(华东)石油工程学院;
3. 江苏省海洋油气钻井装备重点实验室
2. School of Petroleum Engineering, China University of Petroleum(Huadong);
3. Jiangsu Provincial Key Laboratory of Marine Oil and Gas Drilling Equipment
0 引言
我国天然底水油藏储量较为丰富,随着油藏开采进入后期,其特征也逐渐趋向于底水油藏[1]。底水油藏开采的关键就是抑制水锥,目前主要的措施有优化射孔、控制临界产量和临界压差、在油水界面附近打人工隔板、开发中后期加密井调整技术和排水采油技术等[2]。前4种措施只能在一定时期内保持油水界面的相对稳定,极大地限制了油井的产能。排水采油技术可降低含水率的增长速度,恢复和提高油井产量,能较好地解决底水锥进问题。排水采油技术主要包括双层完井抑制水锥技术和双管同采抑制水锥技术,目前采用较多的是双管同采抑制水锥技术,但由于该技术投资大,风险高,限制了其应用和发展[3]。基于双层完井的单管排水采油技术具有工艺简单和老井改造成本低等优点,是解决底水油藏最有效和最经济的方法之一。笔者提出了一种基于电潜泵-射流管柱的单管排水采油工艺方案,并对工艺中的射流管柱进行了设计和优化,形成了单管排水采油工艺综合配套技术,达到了有效开发底水油藏的目的,该技术可为我国底水油藏开发提供技术支撑。
1 底水油藏单管排水采油工艺 1.1 单管排水采油整体工艺方案底水油藏开采的关键就是解决底水锥进问题。笔者提出了一种基于电潜泵-射流管柱的底水油藏单管排水采油工艺(见图 1)。该工艺主要由电潜泵总成、射流管柱、封隔器及单向阀等部分组成。

|
| 图 1 基于电潜泵-射流管柱的底水油藏单管排水采油工艺 Fig.1 Single tube water drainage and oil production technology for bottom water reservoir based on electric submersible pump-jet pipe 1—井口;2—电潜泵总成;3—丢手接头;4、6—封隔器;5—射流管柱;7—单向阀。 |
工艺原理:以高压底水为动力液,利用射流原理,当高压底水流经喷嘴时,速度提高,压力降低,当压力降低于油层流压时,即可将油液吸入射流管柱内,经过喉管和扩散管与底水混合,再由电潜泵将油水混合液排至地面。
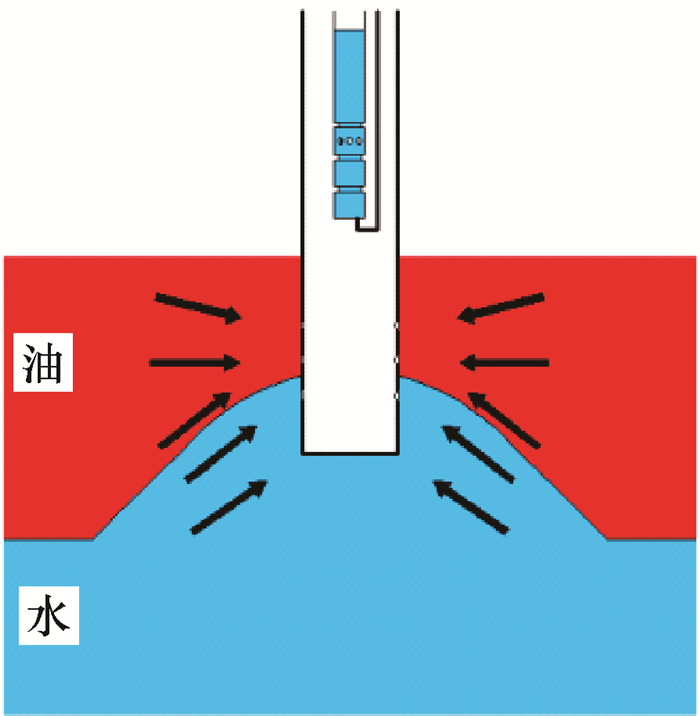
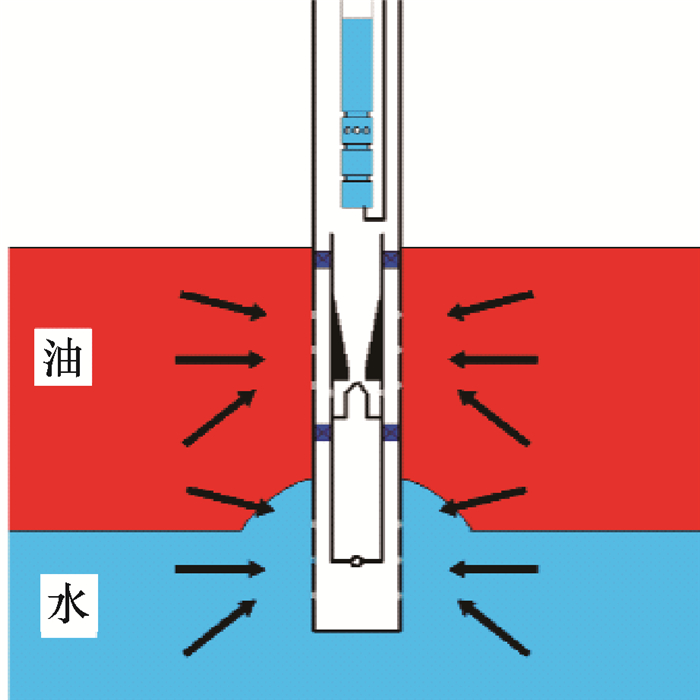
普通单管采油工艺在采油时,由于油层油液的流动,会导致套管临近处地层油压降低,此时高压底水将锥进油层(见图 2),阻碍油流通道,导致产液含水率极高,严重时底水会完全将油流通道堵住,形成死油区,大大降低了采收率。而基于电潜泵-射流管柱的底水油藏单管排水采油工艺采油时,会抽取大量的底水,降低套管临近油水界面处底水的压力,从而达到降低水锥的目的(见图 3)。
|
| 图 2 常规单管采油底水锥进 Fig.2 Bottom water coning with conventional single tube production |
|
| 图 3 单管排水采油工艺降水锥 Fig.3 Water coning reduction by applying single tube water drainage and oil production |
1.2 单管排水采油工艺仿真模拟
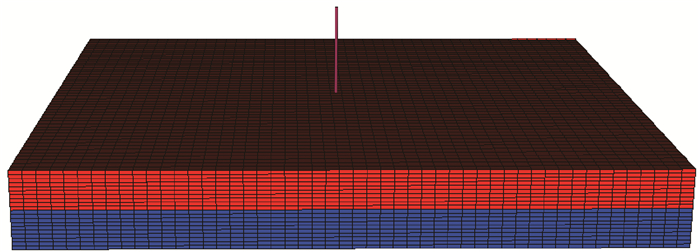
用Eclipse软件建立胜利油田某试验井的模型,模型长400 m,宽400 m。平面网格尺寸为5 m×5 m,纵向上为1 m。生产井位于模型中心,并利用虚拟井技术在底部水层进行排水。单井三维地质模型见图 4。利用该模型对普通单管采油工艺和基于电潜泵-射流管柱的单管排水采油工艺进行模拟,设置产液速度50 m3/d,射孔打开程度30%,排水速度210 m3/d,排水层位靠近油水界面,模拟预测时间10 a。模拟结果如图 5及图 6所示。
|
| 图 4 单井三维地质模型 Fig.4 Single well with 3D geological model |
|
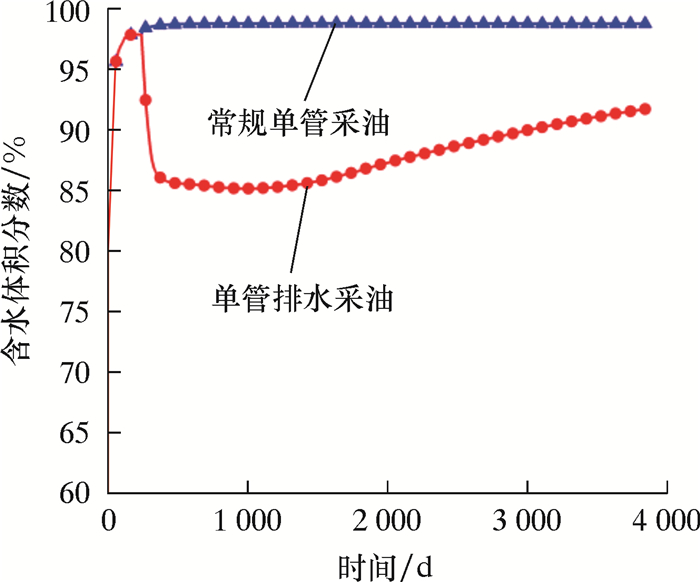
| 图 5 试验井预测含水体积分数对比图 Fig.5 Comparison of predicted water volume fraction in the test well |
|
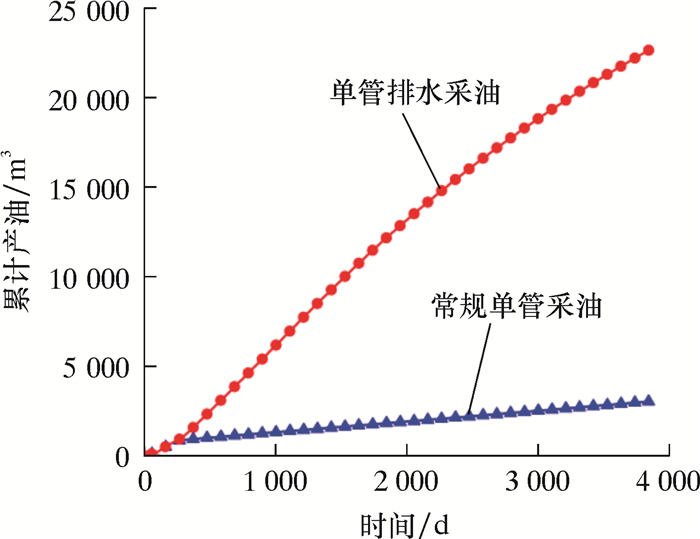
| 图 6 试验井预测累计产油对比图 Fig.6 Comparison of predicted cumulative oil production of the test well |
由图 5可知,普通单管采油工艺在生产约150 d后,产液含水体积分数便达到98%,此时采用排水采油工艺,在使用该工艺约1 a后,可将产液含水体积分数降低至86%,开采9 a后,含水体积分数仅升高至90%,可见单管排水采油方案对降低含水体积分数有显著的效果。由图 6可知,10 a以后,普通单管采油工艺累计产油3 029 m3,单管排水采油工艺累计产油22 680 m3,单管排水采油工艺比普通单管采油工艺增产原油19 651 m3,增油效果明显。
2 射流管柱设计 2.1 射流管柱结构设计根据单管排水采油工艺对射流管柱的结构要求进行射流管柱结构设计。单管排水采油工艺的作业过程如下。
(1) 下连接管柱。将单向阀+油管+液压式封隔器+射流管柱+液压式封隔器+丢手接头+油管至井口的连接管柱下到特定位置。
(2) 坐封。井口憋压至坐封压力,封隔器进行坐封。
(3) 通过一定的作业手段,使得射流管柱与油层构成油流通道。
(4) 起出丢手管柱。
(5) 下放电潜泵。
(6) 进行排水采油作业。
根据工艺作业过程,在管柱坐封时要求射流管柱密封,在坐封完成之后,通过一定的作业手段使射流管柱打开。据此要求设计了射流管柱(见图 7)。管柱坐封完成后,油管内继续加压,剪断剪钉,打开滑套,使得射流管柱与油层构成油流通道。采油时,底水通过油管进入射流管柱,当底水进入喷嘴时,速度升高,压力降低,低于油层流压,油层中的油液通过开孔管中的孔被吸入到射流管柱内,通过喉管与底水混合,通过扩散管将油水混合液动能转化为压力能,再由上部的电潜泵总成排至地面。

|
| 图 7 射流管柱结构图 Fig.7 Structure of jet string 1—上接头;2、5、9、12、13—O形密封圈;3—连接管;4—扩散管;6—开孔管;7—喉管;8—剪钉;10—喷嘴;11—滑套;14—下接头。 |
2.2 射流管柱参数计算 2.2.1 假设条件
(1) 地层水和地面水体积变化很小,可视为不可压缩流体,即其流量和密度都不变。油液体积发生变化,但由于含水较高,其变化对混合液的影响较小,也可忽略不计;
(2) 地层水和地层油液混合时不考虑热交换。
2.2.2 基本尺寸计算[4]喷嘴直径计算式为:
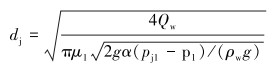
|
(1) |
喉管直径计算式为:
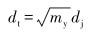
|
(2) |
喉嘴距计算式为:
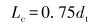
|
(3) |
喉管相对长度为:
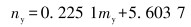
|
(4) |
喉管长度为:
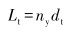
|
(5) |
扩散管长度为:
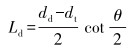
|
(6) |
式中:dj为喷嘴直径,mm;Qw为设计水排量,m3/d;μ1为喷嘴流量系数;α为喉管进口函数;pj1为喷嘴入口压力,MPa;p1为管柱入口处压力,MPa;ρw为地层水的密度,kg/m3;dt为喉管直径,mm;my为最优面积比;Lc为喉嘴距,mm;ny为喉管相对长度;Lt为喉管长度,mm;Ld为扩散管长度,mm;dd为扩散管出口直径,mm;θ为扩散管锥角,(°)。
2.2.3 射流管柱效率计算射流管柱效率计算式为:
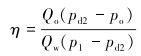
|
(7) |
式中:η为射流管柱效率;Qo为设计油排量,m3/d;po为油层流压,MPa;pd2为扩散管出口压力,MPa。
笔者以胜利油田试验井为例,计算得射流管柱主要参数如表 1所示。
| 参数 | 喷嘴直径/mm | 喉管直径/mm | 喉嘴距/mm | 喉管长度/mm | 喷嘴锥度/(°) | 扩散管锥度/(°) |
| 数值 | 6.4 | 11.0 | 9.0 | 62.0 | 13.5 | 7.0 |
3 射流管柱参数优化
射流管柱的效率直接影响采油工艺的效率,因此,对射流管柱进行优化,优化目标为射流管柱效率η。由式(7) 可得:
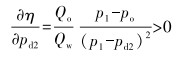
|
(8) |
由式(8)可知,射流管柱效率η与扩散管出口压力正相关,可将扩散管出口压力作为优化函数。
此处采用响应曲面试验结合粒子群优化算法对射流管柱结构参数进行优化。在进行响应曲面试验前,为缩小试验范围,确定最佳值区域,需进行Plackett-Burman试验与最陡爬坡试验。与射流管柱效率有关的结构参数有:喷嘴直径、喉管直径、喉嘴距、喉管长度、喷嘴锥度及扩散管锥度。由于该工艺要求保证喷嘴出口的压力低于油层流压,所以此处不再对喷嘴直径进行优化。射流管柱待优化的结构参数有5个,分别为喉管直径、喉嘴距、喉管长度、喷嘴锥度和扩散管锥度
3.1 Plackett-Burman试验 3.1.1 因子水平设计因子即为上文所述待优化的5个结构参数,每个因子所取的2个水平称为高水平(+1) 和低水平(-1),各因子的水平安排见表 2。
| 因子名称 | 因子代号 | 低水平(-1) | 高水平(+1) |
| 喉管直径/mm | X1 | 7 | 15 |
| 喉嘴距/mm | X2 | 7 | 11 |
| 喉管长度/mm | X3 | 50 | 74 |
| 喷嘴锥度/(°) | X4 | 12 | 15 |
| 扩散管锥度/(°) | X5 | 6 | 8 |
Plackett-Burman试验的试验次数N是4的倍数,N=12、20、24……。对于N次试验至多可研究N-1个因子,但实际因子应少于N-4个,至少要有3个虚构变量用以估计误差[5]。文中待优化参数有5个,因此采用N=12的Plackett-Burman试验设计,试验设计及结果如表 3所示。
| 试验编号 | X1 | X2 | X3 | X4 | X5 | pd2/MPa |
| 1 | -1 | 1 | 1 | 1 | -1 | 17.51 |
| 2 | -1 | -1 | 1 | 1 | 1 | 18.28 |
| 3 | 1 | -1 | 1 | -1 | -1 | 18.17 |
| 4 | -1 | -1 | -1 | -1 | -1 | 17.92 |
| 5 | -1 | 1 | -1 | -1 | -1 | 18.34 |
| 6 | 1 | 1 | -1 | 1 | 1 | 18.31 |
| 7 | 1 | -1 | -1 | -1 | 1 | 17.26 |
| 8 | 1 | 1 | -1 | 1 | -1 | 16.69 |
| 9 | 1 | -1 | 1 | 1 | -1 | 18.21 |
| 10 | -1 | 1 | 1 | -1 | 1 | 17.78 |
| 11 | -1 | -1 | -1 | 1 | 1 | 18.27 |
| 12 | 1 | 1 | 1 | -1 | 1 | 16.64 |
3.1.2 结果分析
因子的主效应(因子处于高水平时试验的平均值与该因子处于低水平时试验的平均值之差)、t值及对应的分布概率P如表 4所示。由表可知,X1对于提高射流管柱效率表现为正效应,X2、X3、X4及X5具有负效应。由于影响因子较少,此处对所有因子进行优化。
| 因子 | 主效应 | 显著性检验 | |
| t | P | ||
| X1 | 9.62 | 5.51 | 0.002 |
| X2 | -3.50 | -2.00 | 0.092 |
| X3 | -4.12 | -2.36 | 0.057 |
| X4 | -0.61 | -0.35 | 0.738 |
| X5 | -1.17 | -0.67 | 0.529 |
3.2 最陡爬坡试验及结果
响应曲面法拟合方程只在考察的紧接邻域里才充分近似真实情形。因此,通过最陡爬坡法以确定试验值变化的梯度方向为爬坡方向,根据各因子效应值的大小确定变化步长,以达到快速、经济地逼近最佳值区域的目的[6]。由Plackett-Burman试验结果设计主要因子的最陡爬坡路径,其中喉管直径具有正效应,应增加;喉嘴距、喉管长度、喷嘴锥度及扩散管锥度具有负效应,应减小。试验设计及结果如表 5所示。
| 试验编号 | X1 | X2 | X3 | X4 | X5 | pd2/MPa |
| 1 | 5 | 12 | 80 | 16 | 10 | 17.85 |
| 2 | 7 | 11 | 74 | 15 | 9 | 18.03 |
| 3 | 9 | 10 | 68 | 14 | 8 | 18.06 |
| 4 | 11 | 9 | 62 | 13 | 7 | 18.25 |
| 5 | 13 | 8 | 56 | 12 | 6 | 18.29 |
| 6 | 15 | 7 | 50 | 11 | 5 | 18.05 |
| 7 | 17 | 6 | 44 | 10 | 4 | 17.55 |
由表 5可知,最优射流管柱效率条件可能在试验4与试验5之间,故以试验5的水平为下一步响应曲面试验设计的中心点。
3.3 响应曲面试验及分析 3.3.1 面心组合设计(CCF)由于扩散管出口压力与5个因子之间的关系未知,所以响应曲面试验设计的第1步是寻求适合扩散管出口压力与5个因子之间真实函数关系的逼近式。在不清楚5个因子是否存在交互作用的情况下,为保证模型的准确性,采用面心组合设计的二阶模型,即有:
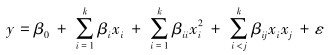
|
(9) |
式中:xi、xj为自变量;βi、βii和βij分别表示一次、二次及交互作用项的回归系数;ε为误差。
试验中,5个因子的中心点水平即为最陡爬坡试验中试验5的水平,低水平和高水平的取值如表 6所示。
| 序号 | 参数 | 中心点(0) | 低水平(-1) | 高水平(+1) |
| 1 | X1 | 14 | 13 | 15 |
| 2 | X2 | 9 | 7 | 11 |
| 3 | X3 | 68 | 62 | 74 |
| 4 | X4 | 10 | 9 | 11 |
| 5 | X5 | 8 | 7 | 9 |
CCF设计试验安排及通过数值模拟所得的结果见表 7。
| 序号 | X1 | X2 | X3 | X4 | X5 | pd2/MPa |
| 1 | -1 | 1 | -1 | 1 | 1 | 17.86 |
| 2 | 0 | 0 | 0 | 0 | 0 | 18.13 |
| 3 | 0 | 0 | 0 | -1 | 0 | 18.07 |
| 4 | -1 | 1 | 1 | 1 | -1 | 18.07 |
| 5 | 0 | 0 | 0 | 0 | 0 | 18.13 |
| 6 | 1 | -1 | 1 | 1 | -1 | 17.49 |
| 7 | -1 | -1 | -1 | 1 | -1 | 17.56 |
| 8 | 0 | 0 | 0 | 0 | 0 | 18.13 |
| 9 | 1 | 1 | 1 | -1 | -1 | 18.17 |
| 10 | -1 | 1 | 1 | -1 | 1 | 18.10 |
| 11 | 0 | 0 | 1 | 0 | 0 | 18.07 |
| 12 | -1 | 1 | -1 | -1 | -1 | 18.12 |
| 13 | 1 | -1 | 1 | -1 | 1 | 17.62 |
| 14 | 1 | 0 | 0 | 0 | 0 | 18.14 |
| 15 | 0 | 0 | 0 | 1 | 0 | 18.14 |
| 16 | 0 | 0 | 0 | 0 | 0 | 18.17 |
| 17 | 0 | 0 | 0 | 0 | 0 | 18.13 |
| 18 | 0 | 1 | 0 | 0 | 0 | 18.13 |
| 19 | 1 | -1 | -1 | -1 | -1 | 18.09 |
| 20 | 0 | 0 | -1 | 0 | 0 | 17.57 |
| 21 | 1 | -1 | -1 | 1 | 1 | 18.37 |
| 22 | 1 | 1 | -1 | 1 | -1 | 17.40 |
| 23 | -1 | -1 | -1 | -1 | 1 | 18.04 |
| 24 | 0 | 0 | 0 | 0 | -1 | 17.70 |
| 25 | 1 | 1 | -1 | -1 | 1 | 17.88 |
| 26 | 0 | 0 | 0 | 0 | 1 | 17.96 |
| 27 | 0 | -1 | 0 | 0 | 0 | 18.09 |
| 28 | 0 | 0 | 0 | 0 | 0 | 18.13 |
| 29 | -1 | -1 | 1 | 1 | 1 | 17.49 |
| 30 | -1 | -1 | 1 | -1 | -1 | 17.60 |
3.3.2 试验结果分析
通过变量代换将多元非线性二阶模型(式(9))转变为多元线性一阶模型,然后进行多元线性回归分析可得式(9) 的系数,从而建立因子与响应值之间的多元回归方程:
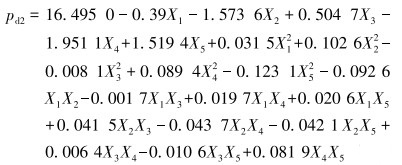
|
(10) |
多元回归模型的方差分析结果如表 8所示。
| 方差来源 | 自由度 | 平方和/MPa2 | F值 | P值 |
| 回归 | 20 | 22.613 | 5.66 | <0.001 |
| 误差或残差 | 11 | 0.633 | — | — |
| 总和 | 31 | 23.246 | — | — |
由表 8可知,回归平方和SSR=22.61 3 MPa2,误差平方和SSE= 0.633 MPa2,总平方和SST=SSR+SSE=23.246 MPa2。调整的决定系数为Radj2,其定义为:
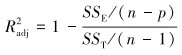
|
(11) |
式中:n为试验次数;p=k+1,k为回归变量个数。
根据表 8,回归方程的调整决定系数Radj2= 0.915,表明仅有约8.5%的试验数据用该模型无法解释,说明此回归方程有意义;而且P<0.001<α=0.01,说明回归方程极显著,即回归方程很好地解释了各因子与扩散管出口压力之间的关系。
3.4 粒子群优化算法寻优为了便于计算,需对5个因子的水平进行编码,使得编码后的水平均在区间[-1,1]内。设xi为因子Xi的编码水平,它与因子的真实水平Xi的关系为:
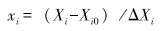
|
(12) |
式中:Xi0为试验中心点处因子的真实值;ΔXi为因子的水平变化步长,即高水平与低水平之差的1/2。编码后各因子与响应值之间的回归模型为:
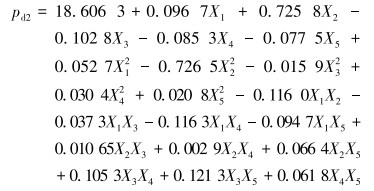
|
(13) |
设置粒子的长度D=5,粒子的范围为[-1,1],粒子种群大小N取40,粒子的最大飞行速度vmax=2,加速因子取c1=c2=2,惯性权重ω采用线性递减权值策略,最大迭代次数Tmax取400。根据PSO算法的理论及计算流程[7-9],采用Matlab编程求解,得到最优解及其对应的真实值,结果如表 9所示。
| 水平 | 因子 | ||||
| 喉管直径/mm | 喉嘴距/ mm |
喉管长度/mm | 喷嘴锥度/(°) | 扩散管锥度/(°) | |
| 编码值 | 0.776 | 0.956 | -0.956 | 0.963 | 0.866 |
| 真实值 | 10.50 | 10.60 | 61.00 | 14.40 | 8.00 |
3.5 优化前、后效率对比
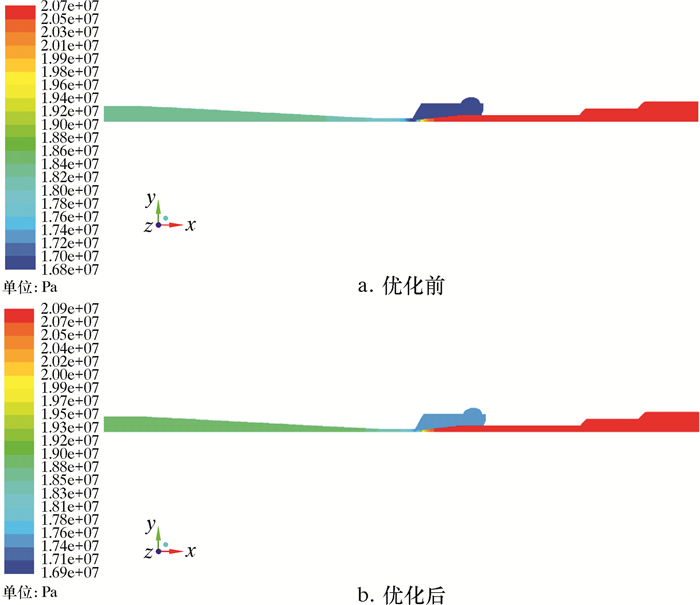
图 8为优化前、后射流管柱内压力分布云图。优化前,出口压力为18.27 MPa,射流管柱效率6.6%,优化后出口压力为18.80 MPa,射流管柱效率16.1%,提升了144%,达到现场应用要求。
|
| 图 8 优化前、后射流管柱内压力分布云图 Fig.8 The inner pressure distribution in the jet pipe before and after optimization |
4 结论
(1) 底水油藏在开采过程中,底水锥进是导致水处理费用增加和开发成本升高的主要原因。对此,在双层完井原理的基础上提出了一种基于电潜泵-射流管柱的底水油藏单管排水采油工艺。介绍了该工艺的降水锥原理,射流管柱的结构设计及优化,并对工艺采油效果进行了仿真模拟。
(2) 数值分析结果表明:在使用该工艺1 a后,可将含水体积分数超过98%的油井的含水体积分数降低至86%,开采9 a后,含水体积分数仅升高至90%,累计油增产可达19 651 m3。
(3) 管柱参数优化结果表明:经过优化射流管柱的效率由6.6%提高到16.1%,优化效果明显,达到了有效开发底水油藏的目的。单管排水采油工艺综合配套技术可为我国底水油藏开发提供技术支撑。
| [1] | 王福林. 底水油藏底水锥进及人工隔层稳油控水机理研究[D]. 大庆: 大庆石油学院, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10220-2010156047.htm |
| [2] | 魏尚武, 李旭东, 李洪成. 吐哈盆地红南边底水油藏开采机理模拟[J]. 新疆石油地质, 2000, 21(2): 141–143. |
| [3] | 马飞英, 王永清, 王慧, 等. 底水气藏气水分层开采技术[J]. 石油天然气学报, 2013, 35(5): 104–107. |
| [4] | 陆宏圻. 射流泵技术的理论及应用[M]. 北京: 水利电力出版社, 1989. |
| [5] | 孟涛, 张应山. 关于Plackett-Burman饱和设计数值分析方法的比较研究[J]. 山西师范大学学报(自然科学版), 2011, 25(1): 7–13. |
| [6] | 李云钊, 宋兴福, 孙玉柱, 等. 基于响应曲面法的反应-萃取-结晶工艺优化[J]. 化工学报, 2016, 67(2): 588–597. |
| [7] | 周文. 粒子群优化算法及其参数设置的研究[J]. 湖北职业技术学院学报, 2006, 9(4): 93–96. |
| [8] | 于颖, 李永生, 於孝春. 基于离散惩罚粒子群算法的波纹管优化设计[J]. 石油机械, 2007, 35(12): 12–15. DOI: 10.3969/j.issn.1001-4578.2007.12.004 |
| [9] | 刘宝宁, 章卫国, 李广文, 等. 一种改进的多目标粒子群优化算法[J]. 北京航空航天大学学报, 2013, 39(4): 458–462. |



