0 引言
水下湿式连接装置是一种暴露于苛刻外部环境(如海水、油液及钻井液等),用来连接电缆和水下用电设备的水下可插拔的连接装置[1],其广泛应用于水下能量分配系统、钻井泵系统及流体加热系统,与采油树和脐带缆等重要部件都有直接联系[2]。湿式电连接器内部是电缆设备。水下湿式电连接器的外头插入到内头腔内固定位置后,腔内电器连通导电,电流经电缆流过接触件导体产生热量,一部分热量通过腔内的液压油对流散失;另一部分热能会以热传导形式传递到密封件和其他元件上,导致其温度升高。
橡胶密封件是一种挤压密封件,当电连接器工作时,密封件在固定压缩率和一定温度作用下经过长时间使用,会因老化产生永久变形而逐渐丧失密封性能,寿命逐渐缩短,最终导致泄漏,使电连接器无法使用。在水下工作时,密封件的泄漏会让海水进入湿式电连接器内部,直接损坏电缆通信件,并污染液压油,造成电连接器无法正常通信,因此电连接器的密封性要求极高,其密封性能的好坏决定其在水下能否正常工作。永久变形和弹力消失是橡胶密封圈失效的主要原因,可将压缩永久变形率作为其密封性能退化的参数[3]。
目前国内对普通陆上使用的电连接器温度场分布的研究有很多[4],但对水下湿式电连接器的研究尚处于空白。国外GISMS和SEACON等公司已经有完整的湿式电连接器成品[5-6],但国外对该技术一直保密。笔者通过建立水下湿式电连接器工作的热分析有限元模型,得到密封件的温度场分布,从而计算其剩余寿命,以期为电连接器的设计制造提供理论基础。
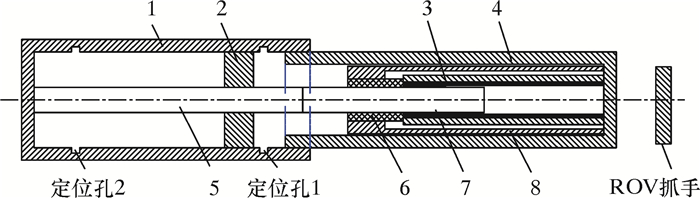
1 模型的建立 1.1 电连接器介绍图 1为单针型电连接器结构示意图。工作时,ROV通过抓手推动外头插入内头腔内,梭针和外头一起向右运动直至其与插针接触,由于内头固定,此时梭针也不再继续运动。定位装置在外头壳体的推动下离开定位孔1向左移动,直至到达定位孔2位置,此时外头完全插入内头内部,两端电缆连接通电。
|
| 图 1 单针型电连接器结构图 Fig.1 Structural schematic of single needle 1—内头壳体;2—定位装置;3—导体;4—外头壳体;5—插针;6—橡胶密封件;7—梭针;8—柔性隔膜。 |
水下电连接器根据不同工况有不同针数型号,笔者研究的电连接器结构为七针型结构,如图 2所示,由7个单芯结构件组合而成,每个单芯结构件都相同,其工作水深为500 m。为保证压力平衡,所有空隙部位都充满了油液。通过分析单芯结构可得到橡胶密封件的温度分布情况。

|
| 图 2 七芯式电连接器模型示意图 Fig.2 Schematic diagram of seven core type electric connector model |
1.2 模型简化
水下湿式电连接器由于其工况特殊,内部元件非常多,结构和元件之间的联系相当复杂,同时电连接器腔内充满油液,在对其做有限元分析时,为了提高计算速度,在保证计算结果准确的前提下,对内部结构做了如下简化处理:
(1) 忽略插针和插孔所连接的电缆,只对插针和插孔导体做热分析;
(2) 忽略各个部件中尺寸较小的倒角、开孔和凸台等细节特征;
(3) 腔内为油液环境,因此外壳对热分析影响不大,忽略所有外壳;
(4) 整个电连接器在深海工作,其腔内油液初始温度设为4 ℃。
图 3为单针结构三维简化图。空腔处都充满了液压油,以保持腔内外压力平衡。当插针向右插入腔内,插针外表面与密封件内表面始终贴紧,以防止腔内腔外液体泄漏,插针接触梭针后推动梭针一起继续向右运动,当插针接触上插孔导体时,电连接器实现了电流连通和信号传递。

|
| 图 3 单针结构三维简化图 Fig.3 Simplified diagram of single needle 1—插针;2—密封件;3—插孔导体;4—梭针;5—柔性隔膜。 |
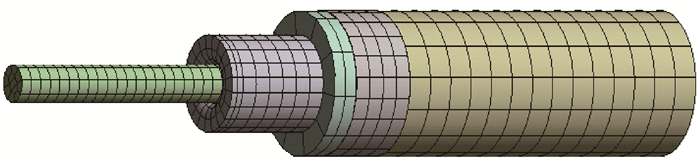
图 4为单针结构的网格划分图。通过对整个结构进行分割处理,使得每个分割部件易于进行网格扫描划分,得到比较规则的网格形状,易于计算分析的快速性和结果精确性,各分割部件之间采用固定连接方式。
|
| 图 4 单针网格划分图 Fig.4 Meshing of single needle |
1.3 热源分析和接触电阻计算
笔者研究的电连接器导通的是直流电,其热源的产生只考虑电阻损耗所产生的焦耳热,因此热源主要来自以下2个方面:① 插针和插孔自身电阻产生的焦耳热;② 插针插孔接触面的接触电阻产生的焦耳热。
电连接器通电工作时,其插针和插孔接触件的发热功率可用欧姆定律表示如下:
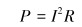
|
(1) |
式中:I为通过接触件的额定电流,A;R为接触件的电阻,Ω。
水下湿式电连接器工作时,插针和插孔导体在接触时会产生接触电阻[7],接触电阻Rj由2部分组成,其值为收缩电阻Rs和表面膜电阻Rb之和,即Rj=Rs+Rb,工程上常用以下经验公式计算接触电阻[8]:

|
(2) |
式中:Rj为接触电阻,mΩ;F为接触压力,N;n为与接触形式、压力范围和实际接触点的数目等因素有关的指数;kj为与接触材料和表面状况等有关的系数,其值由相关文献[8-9]确定。
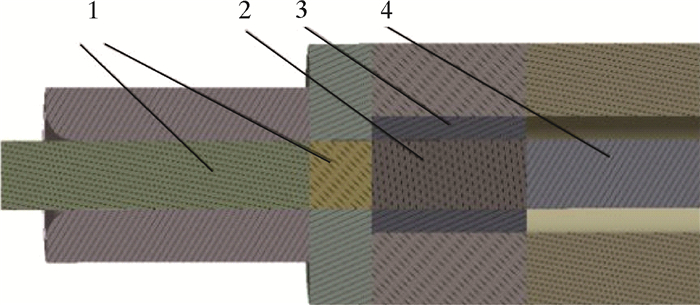
利用等效思想进行有限元仿真分析时,在插针和插孔之间添加一个元件,该元件的总电阻值与接触电阻的阻值相等。图 5为接触电阻等效图。
|
| 图 5 接触电阻等效示意图 Fig.5 Schematic diagram of equivalent contact resistance 1—插针;2—接触电阻等效元件;3—插孔导体;4—梭针。 |
1.4 散热分析和边界载荷
在计算水下湿式电连接器元件的温度场分布时,插针、插孔接触件与橡胶密封件之间通过热传导方式散热,由于腔内充满液压油,油液与固体以对流方式散热。
1.4.1 热传导散热当整个电连接器达到稳定工况时,其内部的传导散热可用如下方程表示[10]。
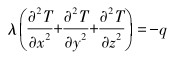
|
(3) |
式中:T为物体的温度,℃;λ为导热系数,W/(m·℃);q为热流率,即单位时间内通过某一截面的热量,W。
采用ANSYS软件进行热电耦合分析时,必须定义材料的电阻率系数ρ和导热率K。电连接器元件用到的相关材料和对应材料系数见表 1。
| 材料 | 材料成分 | 导热率/ (W·m-2·℃-1) |
电阻率/ (Ω·m) |
| 插针 | 黄铜 | 108.9 | 7.1×10-8 |
| 梭针 | 酚醛树脂 | 0.029 | 8.0×10-8 |
| 密封组件 | 丁腈橡胶 | 0.23 | - |
| 柔性隔膜 | 丁腈橡胶 | 0.23 | - |
| 接触电阻等效 | - | 83.7 | 6.3×10-6 |
1.4.2 表面对流散热
采用ANSYS进行热电耦合态分析时,电连接器内的实体与液压油之间的热量交换是表面自然对流换热,对流散热采用牛顿冷却公式[10]:
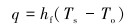
|
(4) |
式中:hf为对流换热系数,W/(m2·℃);Ts为固定表面温度,℃;To为油液的温度,℃。
应用ANSYS中的电热耦合模块对电连接器进行分析,在其插孔导体左侧施加恒定直流电流100 A,如图 6所示。在插针左侧设置一个零电势面,如图 7所示。
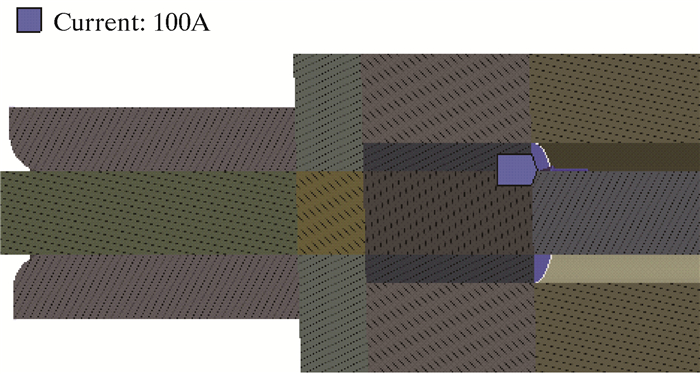
|
| 图 6 电流施加示意图 Fig.6 Schematic diagram of electric current |

|
| 图 7 零电势施加示意图 Fig.7 Schematic diagram of zero potential |
根据前面的模型假设,水下湿式电连接器在深水环境中,其环境温度可设定为4 ℃,整个腔内空间均充满绝缘油,其与实体表面的自然对流换热系数hf为1 000 W/(m2·℃)。图 8为热对流表面和相关系数。
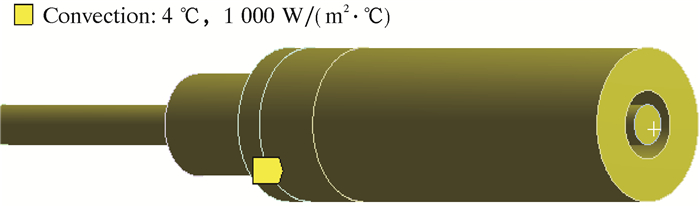
|
| 图 8 热对流表面图 Fig.8 Surface of heat convection |
2 仿真分析结果
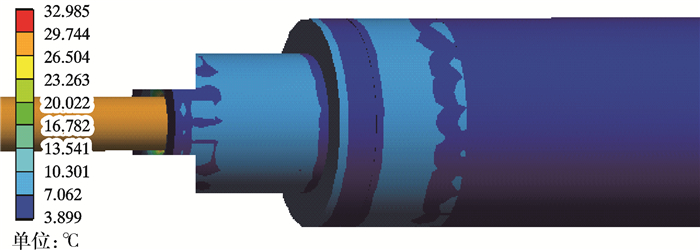
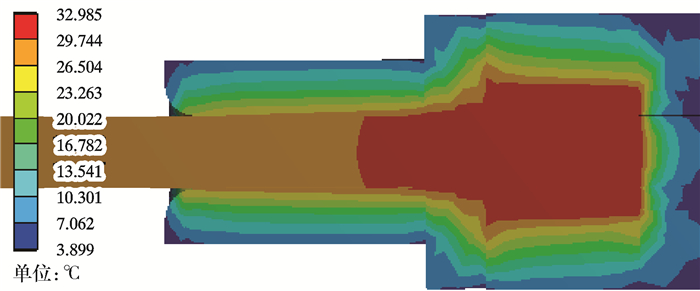
图 9为单芯电连接器模型的整体温度云图。将模型剖开后截面的温度云图如图 10所示。
|
| 图 9 整体温度分布云图 Fig.9 Overall temperature distribution |
|
| 图 10 Overall temperature distribution Fig.10 Overall temperature distribution along longitudinal section |
由图 9可知,等效元件靠近插针位置处产生的焦耳热最高,即插针和插孔导体的接触面附近产生热量最多,其温度分布最高。由于环境温度为4 ℃,由图 10可知,电连接器的最高温度为32.985 ℃,因此温升达到28.985 ℃。随着远离接触电阻,其温度分布逐渐递减。由于液压油与橡胶表面的对流换热且橡胶导热系数很低,靠近梭针处温升较低,且热量几乎没有传输到橡胶密封件外表面和柔性隔膜上,其温度几乎没有升高。
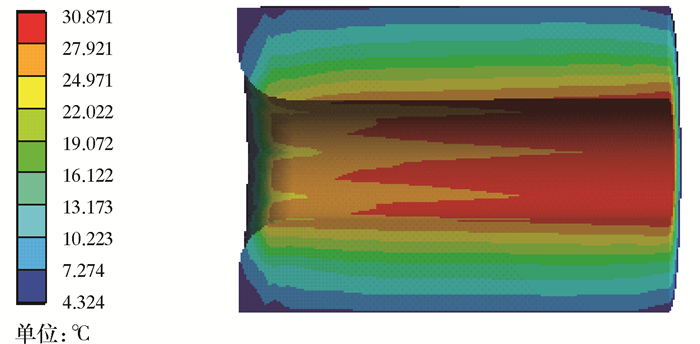
图 11为密封件的温度分布云图。由图可知,密封组件温度升高非常明显,密封件与插针接触面的温度升高较其他位置明显,且靠近右端的位置温度最高,达到30.871 ℃。因此,在电连接器工作过程中,该部位相对橡胶组件其他部位温升较高,其老化程度也会较快,相比其他部位会最先失效。
|
| 图 11 密封件纵向切面温度分布云图 Fig.11 Temperature distribution along longitudinal section of the seal |
3 老化寿命预测理论 3.1 理论基础
老化性能参数P与老化时间t的关系可用以下经验公式表示[11]:

|
(5) |
式中:ε为压缩永久变形率,A为试验常量,a为常数,K为随试验温度T而变的反应速率常数。
K在一定温度范围内符合阿伦尼乌斯方程[12]:
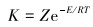
|
(6) |
式(7) 中,Z为频率因子,d-1;E为表面活化能,J/mol;R为气体常数,J/(K·mol);T为老化温度(开氏温度),K。
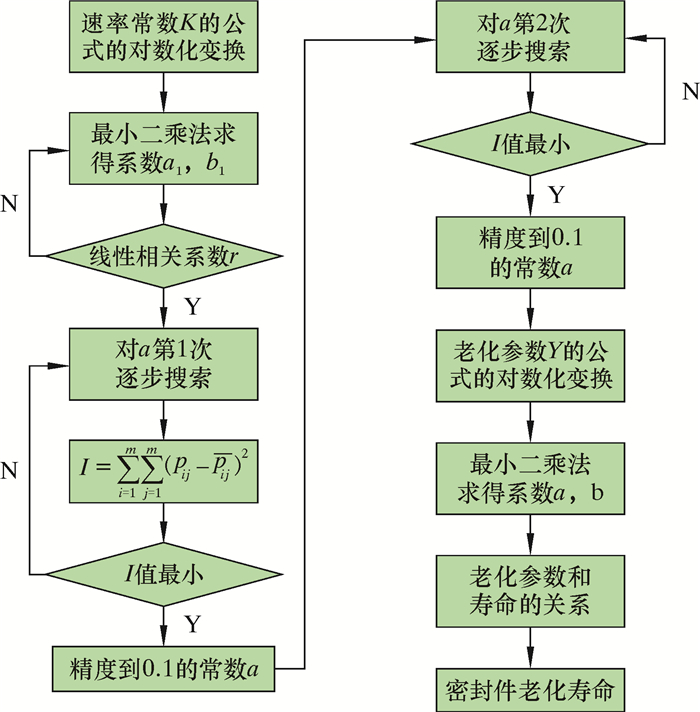
其寿命求解的算法思路如图 12所示。
|
| 图 12 寿命预测的计算流程图 Fig.12 Flow diagram of life prediction calculation |
3.2 计算方法 3.2.1 求常数K的值
将公式(5) 进行对数变换以后,得到其变换公式为:
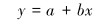
|
(7) |
式(7) 中,x=ta, y=lnP, a=lnA, b=-K。
通过样本数据[13](xi, yi),方程系数a和b可用最小二乘法求得。
式(7) 中斜率的绝对值|b|为橡胶密封件在特定温度下老化反应速度常数。
同样对公式(6) 进行对数变换,得到其变换公式为:
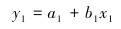
|
(8) |
式(8) 中,x1=T-1, T=273±Q,y1=lnK,a1=lnZ, b1=-E/R,同样用最小二乘法求系数a1和b1。
依据式(8) 计算密封件工况温度Ts的老化反应速度常数的均值K。
3.2.2 求a的最佳值采用逐步搜索的方法:由经验知a是一个精确到0.01的小于1的数值,且其具体值由I值确定,当I最小时,其对应的a即为所求的最优值。I的表达式为[14]:
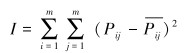
|
(9) |
式中:Pij为第i个热老化试验温度下第j个测试点的性能参数的试验值; Pij为第i个热老化试验温度下第j个测试点的性能参数的预测值[15]。
当I达到最小时,a值即为所求的数值,a值的求取由逐步搜索法来完成。利用计算机编程, 采用2次逐步尝试的方法,第1次尝试:使a尝试0.1、0.2、0.3、……、1.0等的10个值,直接找出所对应的I最小值;第2次尝试:从第1次找的最小值an附近寻找更精确的最优值,使a尝试an-0.09,an-0.08,……,an,……,an+0.08, an+0.09这20个值,找出所对应的I的最小值。
4 模型结果以上算法通过matlab编程实现程序运算,笔者编写了一个关于基于统计方法推算的Matlab函数:lifecalculation(c, P0),其中:c为摄氏温度, ℃;P0为丁腈橡胶的压缩永久变形率临界值。
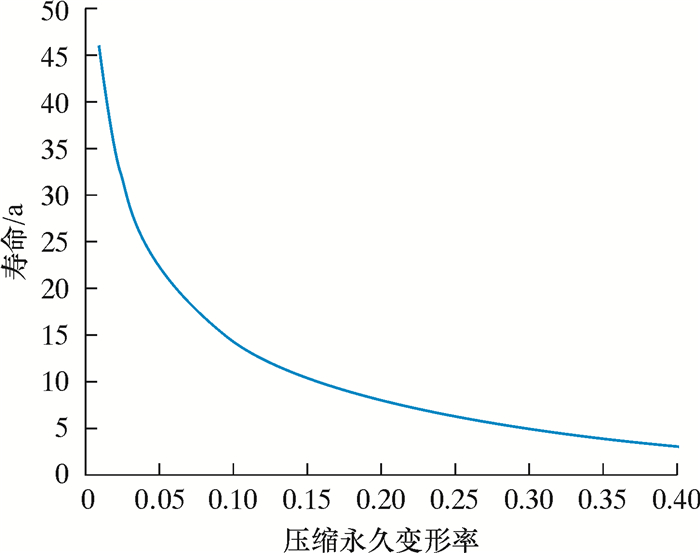
通过程序循环利用该函数,当密封件温度为30.871 ℃时,在不同的压缩永久变形率下,丁腈橡胶的寿命曲线如图 13所示。
|
| 图 13 温度恒为30.871 ℃时寿命与压缩永久变形率关系图 Fig.13 Relation of life and permanent compression deformation rate under the temperature of 30.871 ℃ |
由图可知,当水下湿式电连接器在工况温度30.871 ℃下时,寿命随着压缩永久变形率增大而减小,且压缩永久变形率越大,其寿命值减小得越缓慢。当压缩永久变形率在0.1以内时,寿命能保持15 a以上。当压缩永久变形率到达0.4左右时,寿命值趋于较稳定状态,但是寿命很短,大致为5 a。因此,在保证良好密封的同时,控制橡胶密封件较小的接触压缩应力,能减小其压缩永久变形率,从而获得较长的使用寿命。
5 结论及建议(1) 对热电耦合进行有限元分析,得到水下湿式电连接器整体温度分布情况。插针和插孔导体的接触面位置处由于电阻相对较高,其温度分布最高。因此其接触面处温度沿着腔内方向递增,当电连接器工作时,橡胶密封件的温度最高可达30.871 ℃。
(2) 通过对数变换并利用计算机编程求解了老化寿命计算的相关系数。在计算系数a时,利用2次逐步搜索法寻找其最佳值,相比传统方法减少了搜索时间和计算机的运算量。
(3) 利用matlab建立关于温度和压缩永久变形率的寿命预测函数。利用该函数得到橡胶密封件在一定温度下,寿命随着压缩永久变形率增大而减小,且压缩永久变形率越大,其寿命值减小得越缓慢。
(4) 建议获取丁腈橡胶在不同温度下的应力松弛和时间的试验数据,将应力松弛作为老化寿命性能参数能更直观地体现橡胶的寿命计算。
| [1] | 任万滨, 崔黎, 翟国富, 等. 电连接器接触件插拔特性与接触电阻的仿真分析[J]. 机电元件, 2012, 32(3): 40–44. |
| [2] | 叶杨高, 朱家远, 李锦华. 国外水下插拔光纤连接器的发展[J]. 光纤与电缆及其应用技术, 2008, 2(2): 1–4. |
| [3] | 肖坤. 某弹用O型橡胶密封圈加速退化试验研究[D]. 南京: 南京理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10288-1014175854.htm |
| [4] | 文艺. 电连接器温度场数值分析研究[D]. 天津: 河北工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10080-1013010652.htm |
| [5] | 张利彬. 耐腐蚀深水分离电连接器技术研究[D]. 杭州: 浙江大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015630303.htm |
| [6] | 王存明, 米智楠. 水下插拔连接器的选用[J]. 流体传动与控制, 2009(5): 44–46. |
| [7] | 刘俊俊. 电连接器贮存可靠性加速寿命试验的研究[D]. 杭州: 浙江理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10338-1011015327.htm |
| [8] | 许军, 李坤. 电接触的接触电阻研究[J]. 电工材料, 2011, 1(1): 10–13. |
| [9] | 余玉芳. 机电元件技术手册[M]. 北京: 电子工业出版社, 1992. |
| [10] | 沉维道, 童钧耕. 工程热力学[M]. 3版. 北京: 高等教育出版社, 2001. |
| [11] | 陈海建, 滕克难, 李波, 等. 基于修正Arrhenius方法的SRM药柱储存寿命预估[J]. 弹箭与制导学报, 2011, 31(4): 232–239. |
| [12] | KENNETH G, ROBERT B, DORA K D. Evidence of non-Arrhenius behaviour from laboratory aging and 24-year field aging of polychloroprene rubber materials[J]. Polymer Degradation and Stability, 2005, 87(1): 57–67. DOI: 10.1016/j.polymdegradstab.2004.06.010 |
| [13] | 全国橡胶与橡胶制品标准化技术委员会密封制品分技术委员会. 静密封橡胶零件贮存期快速测定方法: HGT 3087-2001[S]. 北京: 中国标准出版社, 2002. |
| [14] | 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008. |
| [15] | 关进创. 轴承橡胶密封材料寿命预测方法的研究[D]. 大连: 大连海事大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10151-1011118923.htm |



